Варшавский В. И., Поспелов Д. А

Вид материала

Документы

Содержание Станислав Ежи. Лец

Подобный материал:

• Герберт Александер Саймон Исследователи ии: Лотфи Заде Исследователи ии: А. А ляпунов,, 9.34kb.
• «Как привлечь средства государственных институтов развития» Варшавский Владислав Римович, 48.54kb.
• Аннотация к научно-образовательному материалу, 114.81kb.
• 141. Поспелов В. И., Стальнов В. С. Содружественная аккомодация глаз при дисбинокулярной, 167.36kb.
• Тезисы докладов участников III международного конгресса «Россия и Польша: память империй, 1372.37kb.
• Д. А. Поспелов, Г. С. Осипов, 487.33kb.
• Варшавский А. С. Следы на дне, 1828.32kb.
• Рабочая программа учебной дисциплины Для направления 080100. 62 «Экономика» (программа, 562.39kb.
• Диспут с Пирром: прп. Максим Исповедник и христологические споры VII столетия / Отв, 73.89kb.
• Программа дисциплины: Имитационные модели для направления Прикладная математика и информатика, 120.53kb.

Глава 3 СОГЛАСОВАННОСТЬ БЕЗ ДОГОВОРЕННОСТИ


"В действительности все выглядит иначе, чем на самом деле".

Станислав Ежи. Лец


§ 3.1. История начиналась в Арбатове

«И вот, наконец, ранней весной 1928 года почти все известные дети лейтенанта Шмидта собрались в московском трактире, у Сухаревой башни. Кворум был велик — у лейтенанта Шмидта оказалось тридцать сыновей в возрасте от восемнадцати до пятидесяти двух лет и четыре дочки, глупые, немо­лодые и некрасивые.

В краткой вступительной речи Балаганов выразил надежду, что братья найдут общий язык и вырабо­тают, наконец, конвенцию, необходимость которой диктует сама жизнь.

По проекту Балаганова весь Союз Республик сле­довало разбить на тридцать четыре эксплуата­ционных участка, по числу собравшихся. Каждый участок передается в долгосрочное пользование од­ного дитяти. Никто из членов корпорации не имеет права переходить границы и вторгаться на чужую Территорию с целью заработка.

Против новых принципов работы никто не воз­ражал, если не считать Паниковского, который уже тогда заявил, что проживет и без конвенции. Зато при разделе страны разыгрались безобразные сцены. Высокие договаривающиеся стороны переругались в первую же минуту и уже не обращались друг к другу иначе как с добавлением бранных эпите­тов.

Весь спор произошел из-за дележа участков.

Никто не хотел брать университетских центров. Никому не нужны были видавшие виды Москва, Ле­нинград и Харьков.

Очень плохой репутацией пользовались также далекие, погруженные в пески восточные области. Их обвиняли в невежестве и незнакомстве с лич­ностью лейтенанта Шмидта..

58

— Нашли дураков!— визгливо кричал Паниковский.— Вы мне дайте Среднерусскую возвышен­ность, тогда я подпишу конвенцию.

— Как? Всю возвышенность? — заявил Балага­нов.— А не дать ли тебе еще Мелитополь впридачу? Или Бобруйск?

При слове «Бобруйск» собрание болезненно за­стонало. Все соглашались ехать в Бобруйск хоть сейчас. Бобруйск считался прекрасным высококуль­турным местом.

— Ну, не всю возвышенность,— настаивал жад­ный Паниковский,—хотя бы половину. Я, наконец, семейный человек, у меня две семьи.

Но ему не дали и половины.

После долгих криков было решено делить участки по жребию. Были нарезаны тридцать четыре бумаж­ки, и на каждую из них нанесено географическое название. Плодородный Курск и сомнительный Херсон, мало разработанный Минусинск и почти безнадежный Ашхабад, Киев, Петрозаводск и Чита — все республики, все области лежали в чьей-то заячьей шапке с наушниками и ждали хозяев.

Веселые возгласы, глухие стоны и ругательства сопровождали жеребьевку.

Злая звезда Паниковского оказала свое влияние на исход дела. Ему досталось Поволжье. Он при­соединился к конвенции вне себя от злости.

—Я поеду,—кричал он,—но предупреждаю:

если плохо ко мне отнесутся, я конвенцию нарушу, я перейду границу!

Балаганов, которому достался золотой арбатовский участок, встревожился и тогда же заявил, что нарушения эксплуатационных норм не потерпит.

Так или иначе, дело было упорядочено, после чего тридцать сыновей и четыре дочери лейтенанта Шмидта выехали в свои районы на работу».

Каждый, читавший книгу «Золотой теленок» Ильфа и Петрова, помнит, что Паниковский все-таки нарушил конвенцию. Почему это произошло? И могло ли быть иначе? Может быть, Шура Балага­нов напрасно работал всю зиму над созывом конфе­ренции, напрасно переписывался со знакомыми конку­рентами и передавал незнакомым приглашения через внуков Маркса, может быть беда детей лейтенанта

69

Шмидта заключалась в том, что Шура Балаганов не был знаком с теорией коллективного поведения?

Попытаемся формализовать ситуацию, которую мы будем интерпретировать, как игру К лиц. Участники игры алчны и эгоистичны — их поведение определяется только стремлением к личной наживе. Каждый участник в своем поведении обладает на­бором альтернатив, которые мы будем называть стратегиями — он может произвольно выбрать себе участок, на котором будет промышлять в качестве сына лейтенанта Шмидта. Число альтернатив (стра­тегий, участков) может быть больше числа участни­ков игры (детей лейтенанта Шмидта). Как мы уже видели, в приведенном отрывке из «Золотого телен­ка» участки неравноценны. Каждый участок харак­теризуется некоторым числом, которое мы будем на­зывать мощностью этой стратегии. В первой, простей­шей модели мы будем предполагать, что мощность стратегии, т. е. доход, который может быть извле­чем из участка в течение некоторого, заранее фикси­рованного времени, не зависит от числа промышляю­щих на нем детей лейтенанта Шмидта и делится между ними поровну.

Что означает указанное предположение? Оно оз­начает, что если, например, один сын лейтенанта Шмидта за месяц может извлечь из участка 100 руб­лей, то двое детей извлекут из этого участка по 50 рублей каждый.

Вообще говоря, такое предположение не всегда оправдано — более естественно предположение о том, что общий доход с эксплуатируемого участка возрастает с ростом числа участников эксплуатации, однако, доля, приходящаяся на каждого, уменьшает­ся с ростом числа участников. Например, когда вы собираете в лесу грибы, то для вас очевидно, что чем больше пароду будет в облюбованном вами мес­те, тем меньше грибов вы принесете домой. С другой стороны, общее число грибов, которое будет собра­но, безусловно превысит то количество, которое вы могли бы собрать в одиночку.

В некоторых случаях достигаемый эффект зави­сит от числа участников более сложным образом. На-пример, при охоте на лося или кабана размер охот­ничьего трофея, приходящийся на одного охотника, с ростом числа людей участвующих в охоте, сначала

растет — очень велика вероятность того, что в оди­ночку вы вообще ничего не добудете,— и лишь за­тем начинает резко падать. Начнем, однако, для простоты с первого предположения.

Рассмотрим пример. Пусть имеется 10 игроков и число стратегий (участков) достаточно велико, т. е. превышает число игроков. Пусть мощность первого участка 100 руб. в месяц, а всех остальных участ­ков—по 40 руб. в месяц. Допустим, что двое са­мых проворных игроков захватят первый участок и будут получать по 50 руб. в месяц, тогда как осталь­ные восемь, распределившись по одному на осталь­ных участках, будут получать по 40 руб. в месяц. В этой ситуации никому невыгодно менять свой участок. Действительно. Мы отбрасываем, как совер­шенно неразумное, желание прийти вторым на уча­сток с доходом в 40 руб., так как имеется доста­точно свободных участков такой мощности. Перейти с участка с доходом в 40 руб. на участок с доходом в 100 руб. также невыгодно, так как там уже есть два человека и, совершив такой переход, игрок сни­жает свой доход с 40 руб. до 33'/з рубля. Переход с участка с доходом в 100 руб., где участник полу­чает 50 руб., на участок с доходом в 40 руб., также невыгоден. Таким образом, в нашем примере, когда на «богатом» участке функционируют два человека, а остальные участники игры расположены по одному на более «бедных» участках, возникает устойчивая ситуация — никому из участников игры невыгодно в одиночку изменять участок.

Такая ситуация, в которой ни одному из участни­ков игры невыгодно одному изменять свою стратегию, в теории игр называется ситуацией равновесия по Нэшу. Для обозначения ситуации равновесия по Нэшу мы будем использовать термин — точка Нэша.

Здесь уместно заметить, что с точки зрения внеш­него наблюдателя абсолютно безразлично, какие два игрока захватят богатый участок (хотя, как нетруд­но понять, это совсем не безразлично для самих участников). Все ситуации, в которых два человека разрабатывают богатый участок, а остальные по одному распределились на более бедных, являются точками Нэша. Точек Наша в игре может быть мно-го. Действительно, пусть в нашем примере имеются один богатый и двенадцать бедных участков. Тогда

61


существует 45 различных пар участников, которые могут захватить богатый участок, 495 различных способов выбора восьми бедных участков и 40320 спо­собов, которыми восемь участников могут рас­пределиться по этим участкам. Если все эти числа перемножить, то получится число эквивалентных то­чек Нэша в данной игре, равное 898 128 000. Все они характеризуются одним и тем же суммарным доходом и одним и тем же средним доходом, прихо­дящимся на одного участника. Последнее число будем называть ценой точки (или партии) Нэша.

Обратим внимание на следующее обстоятельство: хотя никому из участников невыгодно в одиночку изменять свою стратегию, доход, получаемый всеми участниками, и цена партии не являются максималь­но возможными в этой игре, т. е. их можно увели­чить. В точке Нэша. суммарный доход равен 100 руб. + 8*40 руб.= 420 руб. и цена партии Нэша равна 42 руб. Если же на самом богатом участке разрешить находиться только одному участ­нику, то доход всех участников возрастет на 40 руб. и средний доход каждого участника возрастет до 46 руб. в месяц. Теперь обратим внимание на возни­кающие здесь возможности. В точке Нэша двое участников получают по 50 руб., а остальные по 40 руб. Однако если бы игроки могли договориться, то у двоих доход уменьшился бы на 4 руб. в месяц, зато у восьмерых он возрос бы на 6 руб. в месяц у каждого. Именно в этом месте необходима кон­венция.

Но мы уже видели, что способ, предложенный Балагановым — случайным образом распределить де­тей лейтенанта Шмидта по участкам, не гарантиру­ет устойчивости, а устойчивое распределение приво­дит к потерям. Какие же существуют возможности договориться?

Ограничимся вначале двумя участниками — Балагановым и Паниковским. Балаганову достался участок с доходом 100 руб. в месяц, а Паниковскому — с доходом 40 руб. в месяц. В случае нарушения Паниковским конвенции и его появления в Арбатове доход Балаганова уменьшается до 50 руб. и до той же суммы возрастает доход Паниковского, и нет та­кой силы, которая могла бы удержать Паниковского в Поволжье. Ситуация, в которой и Паниковский а

62

Балаганов занимаются попрошайничеством и вымо­гательством в Арбатове, устойчива — ни одному из них невыгодно перебраться в Поволжье. А между тем, договорившись, они могут существенно повысить свой доход, а путей договориться по меньшей мере три. Во-первых, Балаганов может платить Паниковскому 10 руб. отступного (получая тогда 90 руб), чтобы Паниковский продолжал грабить доверчивых администраторов и общественников Поволжья. Од­нако наглый и вздорный Паниковский вряд ли, даже зная, что без договоренности ему больше не полу­чить, ограничится такой суммой. Во-вторых, Балага­нов и Паниковский могут договориться и периоди­чески меняться участками, что принесет им в среднем по 70 руб. в месяц. Однако естественное недоверие Балаганова к Паниковскому делают мало пригодным и этот способ. В-третьих, Паниковский и Балаганов могли бы просто делить все получаемые деньги по­ровну — такой способ мы будем называть общей кассой. Общая касса, равно как и предыдущий способ, требует определенного уровня доверия участников друг к другу. Кроме того, организация общей кассы может сама по себе потребовать допол­нительных расходов; однако, как бы обременительны они не были, нетрудно видеть, что в случае игры с общей кассой ситуация с максимальным суммар­ным выигрышем устойчива по Нэшу. Все сказанное, естественно, распространяется и на случай с любым числом участников.

Таким образом, мы рассмотрели условия некой игры, которую далее будем называть игрой в размещения, и на примере рассмотрели возникающие в ней устойчивые ситуации. Обстоятельства, модели­руемые этой игрой, могут быть весьма разнообразными. Нас же в этой задаче будет интересовать за­висимость дохода участников игры от их поведения, т. е. от смены стратегии в зависимости от величины текущего дохода.

Для изучения зависимости доходов участников игры от их поведения необходимо формализовать это поведение, т. е. построить модель игрока. Что мы будем понимать под моделью?

Понятие модели достаточно широко и неопреде­ленно. Моделью Паниковского, выбрасываемого из кабинета арбатовского предисполкома, может

63

служить мешок с опилками, модель же Паниковского, принимающего решение нарушить конвенцию, тре­бует более развитых изобразительных средств.

Как мы уже говорили выше, наши игроки стре­мятся лишь к личному обогащению. Единственным критерием, определяющим для них предпочтитель­ность той или иной стратегии, является доход, и, следовательно, модель такого игрока должна быть моделью устройства, оптимизирующего свой выигрыш на дискретном множестве действий. Здесь уместно вспомнить об автоматах, обладающих целесообраз­ным поведением в случайных средах. Подобные авто­маты как раз и являются устройствами, выбирающи­ми свои действия так, чтобы увеличивать свой выиг­рыш. Но для того чтобы ввести в нашу игру такие автоматы, мы должны несколько изменить условия самой игры.

Действительно, наши игроки получают в зависи­мости от выбранной стратегии тот или иной доход (или убыток), а автоматы получают на выбранной стратегии всегда одинаковый выигрыш или проиг­рыш, но с различными вероятностями. Подобное изменение правил игры не связано с принципиаль­ными затруднениями, а в случае с детьми лейтенан­та Шмидта быть может даже более желательно — нахальные отпрыски легендарного героя просят всегда по максимуму, но в зависимости от эксплуати­руемого участка их просьбы удовлетворяются с раз­личной вероятностью. Бывают случаи, когда резуль­татом являются потери, причем не только моральные, но и материальные.

Мощность стратегии будет характеризовать сред­ний выигрыш на этой стратегии при фиксированном значении единичной платы (выигрыша или проигры­ша). Так, например, если в 75 % случаев на данной стратегии игрок получает 200 руб., а в 25 % случаев он выплачивает ту же сумму, то его средний выиг­рыш на этой стратегии равен 100 руб. Средний вы­игрыш, равный 40 руб., обеспечивается 60 % выигры­ша и 40 % проигрыша тех же 200 руб.

Нетрудно понять, что для каждой игры, заданной мощностями стратегий в абсолютных выигрышах и проигрышах, можно построить эквивалентную игру, где выигрыши и проигрыши имеют фиксированное значение, но каждый раз определяются с вероят-

64

костью, зависящей от выбранной стратегии. Таким образом, мы далее будем рассматривать игры со случайными единичными выигрышами и проигрыша­ми, в которых в качестве игроков выступают автома­ты, обладающие целесообразным поведением в слу­чайных средах. Тем самым, вместо исходной ситуации мы имеем ее формальную модель, в которой мож­но изменять параметры: характеристики стратегий и характеристики игроков, и в зависимости от значе­ний указанных параметров изучать протекание игры. Игра состоит в последовательном разыгрывании пар­тий.

При описании автоматов, обладающих целесооб­разным поведением в случайных средах, мы ввели их характеристику—глубину памяти. Глубина памя­ти автомата характеризует, с одной стороны, его конструктивную сложность, а с другой, его способ­ность к усреднению. Она проявляется в длитель­ности времени, за которое автомат способен учиты­вать свои выигрыши и проигрыши. Мы можем счи­тать, что в нашей модели глубина памяти автоматов есть некоторая характеристика способностей игроков к оценке текущей обстановки, так сказать, их интел­лектуального уровня.

Как же зависят результаты игры от интеллекту­альных возможностей участвующих в ней игроков? Здесь уместно еще раз заметить, что понятие интел­лектуального уровня весьма условно и относится только к способности усреднять свои выигрыши и проигрыши. Игроки располагают примитивной инфор­мацией об игре. Они не знают ни числа остальных участников игры, ни сложившейся в игре ситуации, ни даже того, в какую игру они играют. Ничего, кроме собственных выигрышей и проигрышей, на ос­новании которых игроки (автоматы) выбирают свои стратегии. Но именно этот примитивизм позволяет изучать возникающие в игре эффекты в чистом виде.

Поскольку для внешнего наблюдателя все игроки одинаковы, а при случайных выигрышах и проигры­шах автоматы, вообще говоря будут некоторым слу­чайным образом блуждать по стратегиям, то мы будем характеризовать результаты игры математи­ческим ожиданием среднего выигрыша автомата в игре, что эквивалентно математическому ожиданию суммарного выигрыша всех автоматов в игре.

6
5


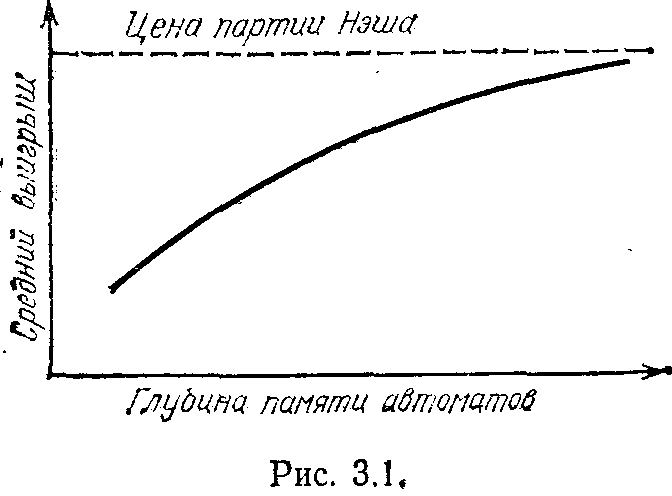
Анализ поведения целесообразных автоматов в этой игре показывает, что с ростом глубины памяти, т. е. с ростом целесообразности поведения такого ав­томата в стационарной случайной среде, растет целе­сообразность его поведения в игре. Последнее озна­чает, что с ростом глубины памяти растет и средний выигрыш автоматов в игре, стремясь к цене партии Нэша так, как показано на рис. 3.1.


К
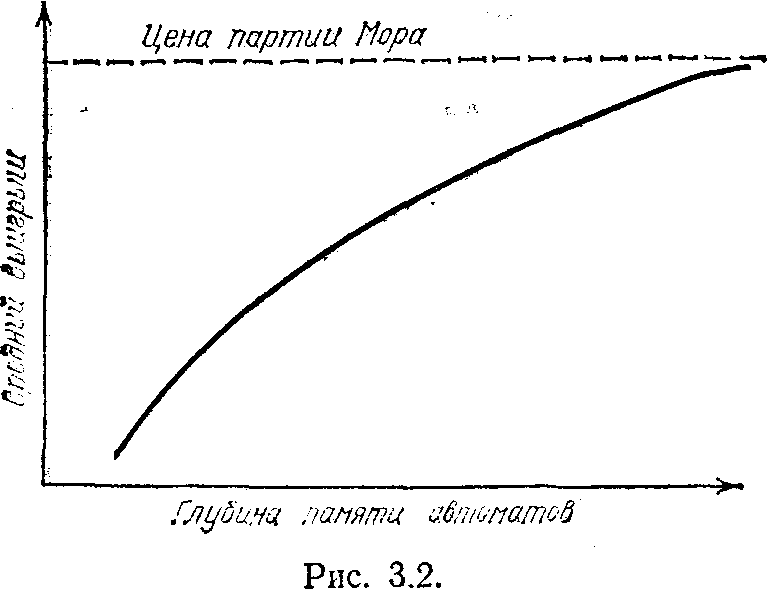
ак мы уже говорили, средний выигрыш в партии Нэша отличен от максимально возможного в иг­ре. Мы также видели, что введение процедуры общей кассы делает партию максимальной цены ус­тойчивой по Нэшу. Устойчивая по Нэшу партия мак­симальной цены называется точкой Мора или пар­тией Мора. На рис. 3.2 приведена зависимость сред­него выигрыша автоматов от глубины их памяти в игре с общей кассой. Внешне эта зависимость мало

66

чем отличается от зависимости в игре без общей кассы. Действительно, и в том, и в другом случаях с ростом глубины памяти средний выигрыш возра­стает и стремится к цене партии Нэша. Разница за­ключается в том, что во втором случае цена партии Нэша выше и называется ценой партии Мора. Какой же полезный вывод можно сделать из приведенных рисунков? Какую интересную и полезную информацию можно извлечь из модели? На первый взгляд, очень небольшую.

М
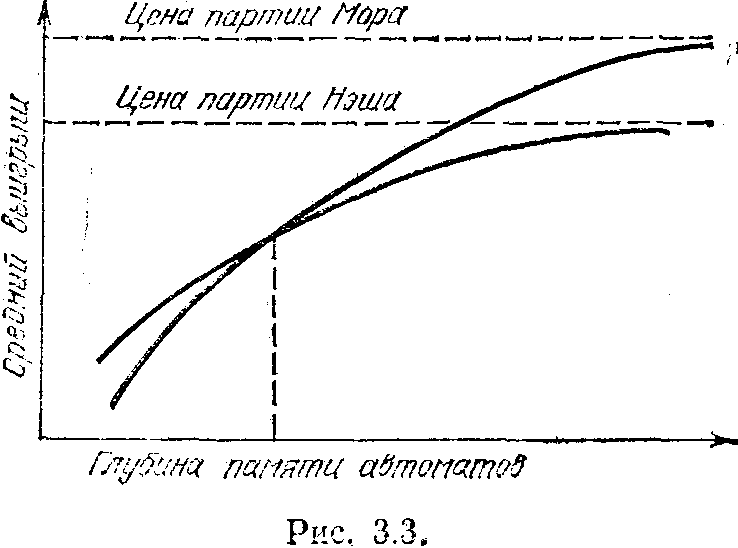
ы увидели, что для достижения точки Нэша необходимо обладать достаточно большой глубиной памяти. В противном случае игроки будут мешать друг другу, снижая тем самым средний выигрыш. Но даже при достаточной глубине памяти для дости­жения максимального выигрыша необходимо при­бегнуть к процедуре общей кассы, т. е. достичь сог­лашения. Постараемся, однако, более внимательно изучить результаты моделирования и совместим рис. 3.1 и рис. 3.2. При этом (рис. 3.3), сразу же обращает на себя внимание следующий факт: процедура общей кассы становится выгодной, лишь начиная с некоторого уровня сложности (!). Выиг­рыш автоматов в игре с общей кассой при глубине памяти ниже критической меньше, чем в игре без общей кассы.

М. Л. Цетлин называл этот эффект «вредом урав­ниловки при низкой сознательности». Вред, однако, зависит не столько от сознательности, сколько от способностей. Действительно, в игре с общей кассой

67


от игрока требуется более тонкая оценка результа­тов своего поведения, чем в игре без общей кассы, где выигрыши и проигрыши более явно зависят от собственного поведения. Процедура общем кассы маскирует зависимость результата от индивидуаль­ного поведения.

Для пояснения сказанного на несколько минут отвлечемся от нашего изложения. Представьте себе молодую девушку, поступившую на химический завод. В ее обязанности входит наблюдение за показаниями приборов. Девушка, как, впрочем, и все ос­тальные работники цеха, получают премию, если качество продукции, выпускаемой цехом, находится в пределах допустимых норм. В течение первых двух месяцев работы девушка читала интересную книгу, от которой она не могла оторваться даже в рабочее время, и очень редко поглядывала на при­боры. На ее счастье в это время не происходило никаких неприятных отклонений процесса от нор­мы, и оба месяца она благополучно получала пре­мию. К началу третьего месяца книга кончилась, новой интересной книги не было и девушке не ос­тавалось ничего иного, как смотреть на приборы. Од­нако именно в этом месяце по причинам, никак не связанным с параметрами процесса, за которыми сле­дила наша героиня, цех дал большое количество брака и премии не было. Трудно предположить, что девушка не сделает вывода о независимости пре­мии от ее поведения. Если бы, с другой стороны, премия с оператора снималась только за незамечен­ные отклонения процесса от нормы, то для правиль­ного выбора линии поведения потребовалось бы го­раздо меньше сообразительности.

Вернемся, однако, к нашей модели. Уже такая простая модель позволяет сделать весьма важный вы­вод—работа по общему критерию становится выгод­ной только при достаточно развитых локальных сред­ствах принятия решений. Если эти средства не обла­дают достаточной сложностью, то, исходя из общего суммарного эффекта, выгоднее, когда каждый участник ориентируется на свой локальный критерий и стремится увеличить свой собственный доход.

На одной из международных конференций нам был задан вопрос: «Не означает ли приведенный вами результат, что при простых средствах управле-

68

ния выгоднее капитализм, а после достаточного раз­вития средств управления становится выгоднее социализм?»

При всей примитивности постановки вопроса, здесь содержится зерно истины. Для полного ис­пользования всех преимуществ социалистического строя необходимы высокоэффективные средства уп­равления. Недаром Владимир Ильич Ленин говорил:

«Социализм — это прежде всего учет». Именно по­этому партия и правительство придают такое большое значение совершенствованию управления.

В заключение разговора о модели «игры в раз­мещения» заметим, что система обладает определен­ного рода надежностью—при выходе из игры одного из участников остальные перераспределяются так. чтобы освободилась стратегия с наименьшей мощ­ностью. Именно про такую ситуацию говорят:

«Когда в учреждении снимают директора, освобожда­ется вакансия уборщицы».

§ 3.2. Когда все одинаковые

Давайте теперь несколько усложним нашу модель. Чем вызвана необходимость ее изменения?

Во-первых, предположение о независимости дохо­да на данной стратегии от числа выбравших эту стра­тегию игроков, как мы уже отмечали в предыду­щем параграфе, не всегда соответствует действи­тельности.

Во-вторых, рассмотренная нами модель имеет содержательный смысл только тогда, когда число игроков меньше числа стратегий. В самом деле, мы оценивали результаты поведения игроков в игре по величине среднего выигрыша, приходящегося на од­ного игрока, или, что эквивалентно, по величине суммарного дохода, получаемого всеми игроками. Нетрудно видеть, что если выигрыш на стратегии не зависит от числа выбравших ее игроков, то любое распределение игроков по стратегиям, при котором на каждой из них имеется по крайней мере по одно­му игроку, обеспечивает максимальный суммарный доход. Более того, с ростом числа игроков будет рас­ти вероятность того, что случайное распределение игроков по стратегиям будет обеспечивать макси­мальный суммарный доход.

69


Содержательный смысл модели для большого числа участников восстанавливается, как только мы введем зависимость мощности стратегии от числа выбравших ее игроков. Рассмотрим, какими могут быть эти зависимости.

П
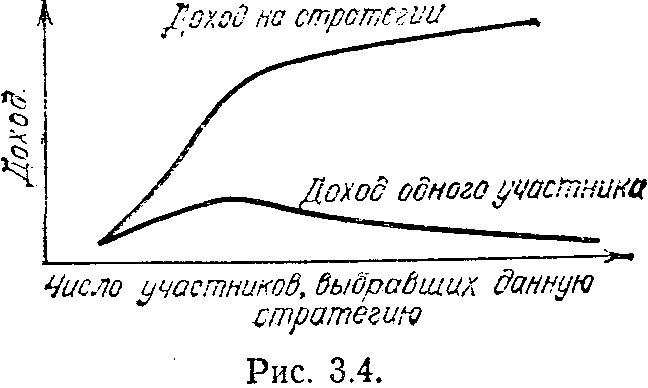
режде всего можно считать, что суммарный до­ход на любой стратегии ограничен некоторой величи­ной. Это означает, что каким бы не было ограничение, начиная с некоторого числа игроков, выбравших данную стратегию, доля, приходящаяся на одного иг­рока, с ростом их числа должна стремиться к нулю, т. е. монотонно убывать. Типичные зависимости тако­го рода приведены на рис. 3.4 и рис. 3.5.

С
ледует заметить, что модель тем привлекатель­нее, чем меньшее число параметров ее задает. Поэто­му постараемся обеспечить в модели возможность исключения такого параметра, как число игроков. Для этого введем зависимость общего дохода на стра­тегии не от числа участников, выбравших данную стратегию, а от их доли от общего числа игроков. Тогда одни и те же функции выигрыша будут опре­делять игру для любого числа участников. Для про-

70

стоты дальнейшего изложения остановимся на случае двух стратегий.

Т
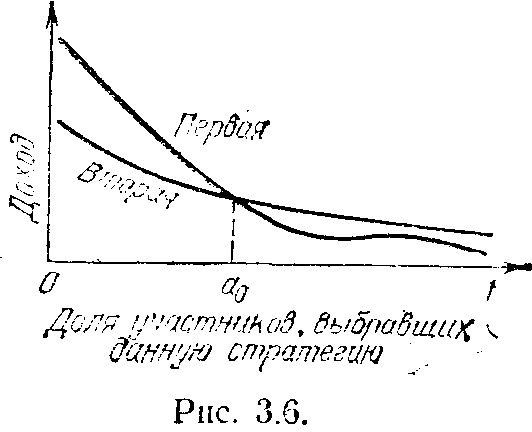
еперь игра задается двумя функциями — зависимостью дохода игроков, выбравших первую страте­гию, от их доли от общего числа игроков и зависимостью дохода игроков, выбравших вторую стратегию, от их доли от общего числа игроков. Нетрудно понять, что обе функции можно представить в виде зависимости от одной переменной — доли игроков, выбравших первую стратегию, так как, задав эту долю, мы автоматически определяем долю игроков, выбравших вторую стра­тегию,— это все осталь­ные игроки. Пример та­ких функций приведен на рис. 3.6.

Как мы уже отметили, выигрыш каждого игрока уменьшается с ростом чи­сла игроков, выбравших одинаковую с ним стра­тегию. С другой стороны, переход игрока, например,

со второй стратегии на первую увеличивает выигрыш игроков, оставшихся на второй стратегии. Какова же ситуация равновесия в такой игре, если игроки инте­ресуются только своими индивидуальными выиг­рышами?

Из рис. 3.6 видно, что правее точки а0 выигрыш каждого участника на второй стратегии выше, чем на первой, к смена первой стратегии на вторую выгодна для игрока. Однако переход игрока с первой страте­гии на вторую уменьшает долю игроков, выбравших первую стратегию, смещая ее к точке а0. Левее точки а0 выгоднее оказывается первая стратегия, и пе­реход игроков со второй стратегии на первую увели­чивает долю игроков на первой стратегии, смещая ее к точке а0. В точке же а0 выигрыши на обеих стра­тегиях одинаковы. Если в точке а0 игрок перейдет с первой стратегии на вторую, то доля игроков, выбрав­ших первую стратегию, уменьшится и соответственно уменьшится выигрыш на второй стратегии, что дела­ет такой переход невыгодным для игрока, осуществ­ляющего этот переход. Аналогично в точке а0 оказы­вается невыгодным для игрока переходить со второй

71

стратегии на первую. Таким образом, распределение игроков по стратегиям, соответствующее точке а0, устойчиво, никому из игроков невыгодно изменять свою стратегию, т. е. точка а0 является в этой игре

точкой Нэша.

Рассмотрим численный пример. Пусть имеются два лесозаготовительных участка и 100 рабочих, ко­торые могут свободно выбирать себе место работы. На каждом участке количество заготавливаемого леса растет с ростом числа работающих на участке, но производительность труда каждого рабочего, а следовательно, и его зарплата, уменьшаются с увеличением этого числа. Подобный эффект может определяться различными причинами, такими, как особенности организации труда, наличием техники, зависимостью размера премиального фонда от рас­ходования фонда зарплаты и т. п.

Обозначим через Х число рабочих на первом уча­стке, а через Y число рабочих на втором участке, и пусть количество леса, заготавливаемое на участках и измеренное в зарплате, выплачиваемой при этом рабочим, определяется функциями

для первого участка 400*Х—0,02*Х³,

для второго участка 280*Y— 0,4*Y².

Тогда, если 80 рабочих будут работать на первом участке, то общая выработка на этом участке будет равна 21 760 руб., т. е. по 272 руб. на человека. На втором участке при этом будут работать 20 человек, которые обеспечат выработку 5440 руб., т. е. те же, что и на первом участке 272 руб. на одного рабочего. Суммарная выработка на обоих участках равна 27 200 руб., и ни одному из рабочих не выгодно изме­нять место своей работы. Действительно, например, переход рабочего со второго участка на первый уменьшает его заработок на 3 руб.

Однако обратим внимание и на другой процесс. Если рабочий перейдет с первого участка на второй, то его зарплата, равно как и зарплата двадцати ра­ботающих на этом участке рабочих, уменьшится на 40 коп. у каждого. При этом на первом участке у 79 оставшихся там рабочих зарплата возрастет на 3 руб. у каждого. Таким образом, общая выработка на двух участках возрастает за счет рабочих, рабо­тающих на первом участке, на 237 руб. и уменьшится

72

на 8 руб. 40 коп. за счет работающих на втором уча­стке.

Из сказанного видно, что, с одной стороны, распределение рабочих по участкам, при котором 80 че­ловек работают на первом участке, а 20 на втором устойчиво по Нэшу, но, с другой стороны, переход рабочих с первого участка па второй приводит к уве­личению общей производительности. Общая выработ­ка достигает максимума, когда на первом участке остается 51 человек, а остальные 49 работают на вто­ром участке. При этом общая выработка на первом участке становится равной 17748 руб., при заработке каждого рабочего, равном 348 руб., а на втором уча­стке выработка достигает 12740 руб., при заработке каждого рабочего в 260 руб. Выработка на обоих участках при этом возрастает по сравнению с точ­кой Нэша на 12 % и достигает 30488 руб. Для боль­шей наглядности все данные сведены в табл. 3.1.

Таблица 3.1

	Точка Нэша	Точка Мора
Зарплата на первом участке	272	348
Зарплата на втором участке	272	260
Средняя зарплата	272	304,88
Доход на первом участке	21 760	17748
Доход на втором участке	5 440	12740
Суммарный доход	27200	30488

Естественно, что при свободном выборе места ра­боты последнее распределение неустойчиво. Увели­чение заработка па 88 руб. в месяц оправдывает стремление рабочих к переходу со второго участка на первый. Как мы уже отмечали в предыдущем па­раграфе, устойчивость по Нэшу партии максималь­ной цены можно обеспечить введением процедуры об­щей кассы. В нашем примере это означает, что зар­плата рабочих не зависит от того, на каком участке они работают, и определяется суммарной выработкой на обоих участках. В этом случае в партии Мора, т. е. партии максимальной цены, устойчивый по Нэшу заработок каждого рабочего будет равен 304 руб. 88 коп., что превышает заработок в точке Наша. Но для обеспечения устойчивости такого распределения

73

мы должны за разные результаты труда на втором участке платить существенно больше, чем на первом. Как это ни парадоксально, но такое неравенство оплаты за равные результаты труда оказывается вы­годным с учетом общих интересов. Так же выгодной с учетом общих интересов оказывается работа части рабочих с заниженной производительностью труда.

Здесь следует заметить, что, конечно, задача об оптимальном распределении рабочих по участкам может быть решена централизованно. Для этого доста­точно установить на обоих участках оптимальную штатную численность. Однако такое решение пробле­мы, во-первых, будет приводить к явному неудовольствию рабочих по поводу поддержания оптимального соотношения численностей на участках, не говоря уже о социальных проблемах, связанных с явным неравенством в оплате, и, во-вторых, потребует централи­зованного решения задачи об оптимальном распреде­лении трудовых ресурсов. С другой стороны, управле­ние способом оплаты обеспечивает децентрализован­ное решение проблемы распределения, порождаемое совместным (коллективным) поведением самого тру­дового ресурса.

Заметим также, что приведенная нами содержа­тельная интерпретация задачи не исчерпывает все моделируемые такой игрой ситуации. Ряд содержа­тельных примеров легко продолжить как в социаль­ных и производственных, так и в технических систе­мах.

Теперь вернемся к изучению поведения участни­ков рассмотренной игры, которую будем называть «игрой в распределения».

Во-первых, нам надо перейти от функций, опреде­ляющих величины выигрыша, к функциям, опреде­ляющим вероятности единичных выигрышей и проиг­рышей, и, как мы уже говорили, сделать эти функ­ции зависящими не от абсолютного числа игроков, выбравших ту или иную стратегию, а от их доли, С методикой первого перехода мы уже познакомились в предыдущем параграфе. Второй переход так­же не связан с какими-либо трудностями. Рассмот­рим числовые данные предыдущего примера.

Пусть а_{1 и} а₂ (а₂=1—а₁) — доли автоматов, вы­бравших в некоторой партии игры первую и вторую стратегии соответственно. Пусть P₁ и P₂ —вероят-

74

ности единичного выигрыша, равного для нашего примера 400 руб., и, значит, (1—p₁) и (1—p₂) — вероятности единичного проигрыша той же суммы. Тогда функции, задающие игру, определяют математическое ожидание единичного выигрыша при

p₁==1—0,25а₁² и p₂==0,85—0,05а₂.

При а₁==0,8 и а₂==0,2 автоматы, выбравшие первую стратегию, будут выигрывать с вероятностью 0,84 и проигрывать с вероятностью 0,16. Если, как мы пред­положили, единичные выигрыши и проигрыши равны :±400 руб., то математическое ожидание выигрыша на первой стратегии будет равно (0,84—0,16)*400=272 руб., что совпадает с выигрышем в точке Нэша.

Рассмотрим зависимость выигрыша автоматов, моделирующих игроков, от глубины их памяти. Пусть в игре участвуют простейшие автоматы, т. е. автома­ты, которые при выигрыше сохраняют свое действие, а при проигрыше немедленно его изменяют. Легко понять, что вероятность смены действия для такого автомата равна вероятности проигрыша при этом действии. Следовательно, при достаточно большом числе автоматов и при постоянной вероятности проигрыша, в силу закона больших чисел, в каждый мо­мент времени постоянное число автоматов будет по­кидать данную стратегию. Но сказанное справедливо для всех стратегий, и, следовательно, некоторое по­стоянное число автоматов будет в каждый момент приходить на данную стратегию. При этом возможна ситуация динамического равновесия, т. е. ситуация, в которой число покидающих стратегию автоматов рав­но числу выбирающих ее. Для нашего примера такая ситуация определяется уравнением баланса

(1 —p₁)a₁ = (1 —p₂)a₂ или 0,25а₁³ =(0,15+0,05а₂)а₂.

Р
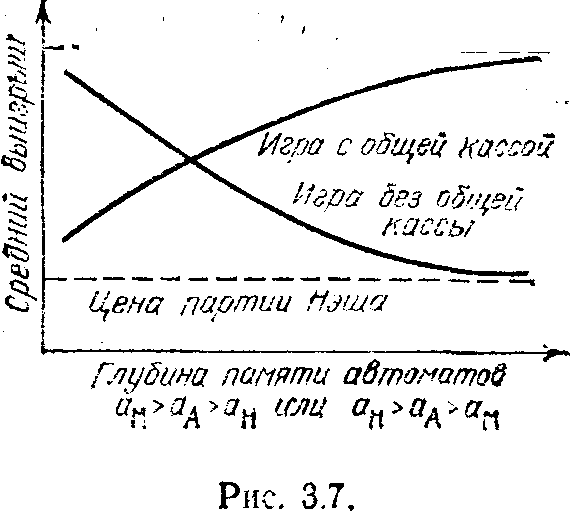
ешением этого уравнения служит а₁=0,63 и а₂==0,37. При этом в каждый момент времени 0,63 всех автоматов будет изменять свою стратегию с пер­вой па вторую и столько же автоматов будет перехо-дить со второй стратегии на первую.

Ситуацию динамического равновесия, порождаемую поведением в игре простейших автоматов, т. е. таких автоматов, у которых вероятность смены дей­ствия равна вероятности штрафа, будем называть точкой Антоса. Увеличение глубины памяти автома-

75

т
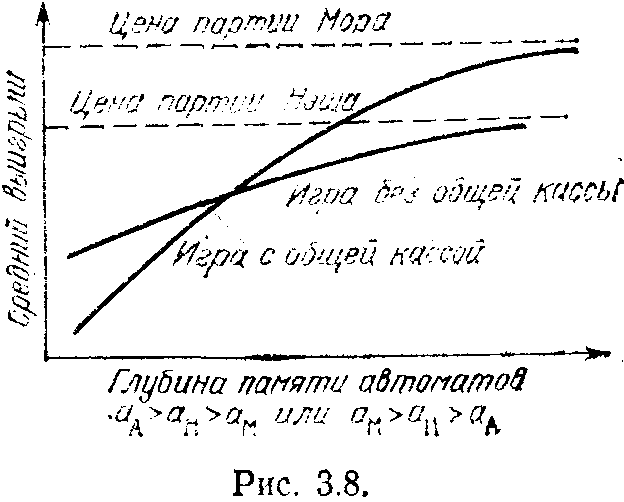
ов уменьшает вероятность смены действия. Однако для каждой вероятности смены действия существует ситуация динамического равновесия, которая, как мы уже говорили выше, с ростом глубины памяти стремится к точке Нэша. Теперь средний выигрыш в игре зависит от взаимного расположения точек, со­ответствующих партиям игры. Обозначим через а_A долю автоматов, выбравших первую стратегию в пар­тии Антоса, через a_н — долю автоматов, выбравших первую стратегию в партии Нэша, и через а_м—долю автоматов, выбравших

первую стратегию в партии максимальной цены. Пусть а_н> >а_А>а_м, что, кста­ти, имеет место в нашем примере, где а_н= =0,8, а_А==0,63, а_м= =0,51. Тогда с ростом глубины памяти рас­пределение автоматов по стратегиям будет удаляться от партии максимальной цены к

партии Нэша и средний выигрыш автоматов будет падать. Действительно, в нашем примере средний выигрыш автоматов в партии Антоса равен 299,28 руб., а в партии Нэша — 272 руб. На рис. 3.7, 3.8, 3,9 приведены типы зависимости среднего выиг­рыша от глубины памяти автоматов при различных типах взаимного расположения точек, соответствую­щих партиям игры,

7
6

Рис. 3.7. демонстрирует нам класс игр, в которых наибольшего эффекта добиваются самые примитив­ные автоматы. Наиболее интересен класс игр, приве­денный на рис. 3.9. В этих играх точка максимальной цены находится между точкой Антоса и точкой Нэша. При этом существует промежуточная и, что наиболее важно, конечная глубина памяти, при которой без процедуры общей кассы достигается партия макси­мальной цены.

Последний факт наводит на размышления о воз­можности организации внешнего оптимизирующего управления, проявляющегося на фоне децентрализо­ванного поведения участников игры. Это управление может быть организовано путем такого искажения функций, определяющих выигрыш на стратегиях, что­бы партия максимальной цены переместилась в интервал между точкой Антоса и точкой Нэша. По­добную деформацию платежных функций можно орга­низовать, например, путем введения некоторого нало­га. Содержательный смысл его введения заключается в том, что прибавление и вычитание констант не из­меняет положения партии максимальной цены, сме­щая вместе с тем положение точек Антоса и Нэша. Более того, константу можно выбрать так, что точка Антоса совпадет с точкой, соответствующей партии максимальной цены, а это означает, что максималь­ного выигрыша в такой игре будут добиваться про­стейшие автоматы.

Возвратимся к нашему численному примеру. Если из суммарного заработка на первом участке изъять 2250 руб. и передать их на второй участок, то точка

77

Антоса совпадет с точкой, отвечающей партии мак­симальной цены, и вероятности выигрыша будут равны





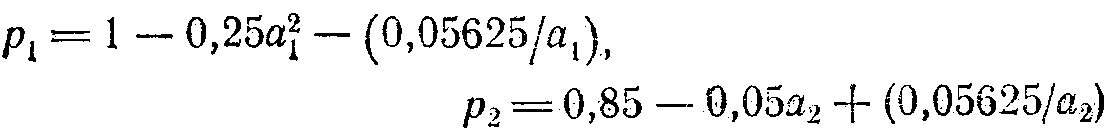
Для тех, кто знаком с теорией игр, должно быть ясно, что указанная процедура эквивалентна реализа­ции оптимальных смешанных стратегий. Заметим также, что для осуществления указанного механизма управления необходимо централизованное определе­ние величины постоянного налога.

Если в игру вводится процедура общей кассы, то выигрыш каждого игрока перестает зависеть от того, какую конкретно стратегию выбрал персонально дан­ный игрок—когда все заработки складываются в общий котел, то все получают одинаково. При этом, однако, величина заработка зависит от того, как иг­роки распределены по стратегиям.

Игра, в которой выигрыш игрока не зависит от того, какую стратегию он выбрал, а зависит лишь от распределения игроков по стратегиям и одинаков для всех участников игры, называется игрой Гура.

Поскольку в игре Гура выигрыши всех автоматов одинаковы, то одинаковы для всех автоматов и вероятности сменить действие и, следовательно, точка Антоса для такой игры независимо от вида платеж­ных функций есть партия, в которой автоматы рас­пределены по стратегиям поровну. Казалось бы, что ситуация в игре Гура не должна изменяться и с ростом глубины памяти участвующих в игре автома­тов — если глубина памяти у всех автоматов одина­кова, то одинаковы и вероятности смены действия, Здесь, однако, срабатывает другой механизм. С рос­том глубины памяти экспоненциально уменьшается вероятность смены действия. Время пребывания ав­томата на стратегии обратно пропорционально веро­ятности смены действия. Чем меньше вероятность проигрыша в некоторой партии игры, тем дольше автоматы пребывают в этой партии. Когда глубина памяти автоматов становится достаточно большой, то даже небольшая разница в вероятностях проигрыша приводит к весьма существенной разнице в вероят­ностях смены действия и, следовательно, в средних

78

временах сохранения неизменности партии. Матема­тический анализ поведения автоматов в игре Гура показывает, что с ростом глубины памяти автоматы начинают преимущественно выбирать стратегии с максимальным временем сохранения неизменности партии, т. е. с максимальным выигрышем.

Заметим, однако, что хотя автоматы с достаточно большой глубиной памяти достигают выигрыша, до­статочно близкого к оптимальному, так как резко увеличиваются времена сохранения неизменности партий, выход на партию максимальной цены с ро­стом глубины памяти требует экспоненциально рас­тущего времени. Последнее соображение полезно по двум причинам.

Во-первых, оно показывает, что выводы, которые делаются на основании рассмотрения средних вели­чин, не всегда справедливы — при таком анализе средних величин в игре Гура автоматы всегда долж­ны разыгрывать партию Антоса.

Во-вторых, игра Гура достаточно хорошо демон­стрирует одну из основных трудностей оптимиза­ции — за достижение оптимума подчас приходится платить так дорого, что оно становится бессмыслен­ным.

Типичным примером являются, например, неко­торые блоки оптимизации в операционных системах вычислительных машин. Если такой блок за 2 ч ра­боты на 5 % увеличивает пропускную способность вычислительной машины, то даже при ее круглосу­точной работе действительная производительность машины не возрастает, а падает на 3 %.

Особенно важно помнить об этом, имея дело с за­дачами оперативного управления — время выхода на оптимальный режим может оказаться таким боль­шим, что к моменту окончания переходного процесса мы окажемся в совершенно новой ситуации, где все надо начинать сначала. С подобной ситуацией мы уже сталкивались, когда говорили о переключаемых случайных средах. Для задачи оперативного управ­ления особенно важны механизмы, которые обеспечи­вают выход на оптимальные режимы при высоко ла­бильных участках, т. е. на нашем модельном уровне, при автоматах с небольшой глубиной памяти.

В заключение данного параграфа заметим, что если в игре Гура средний выигрыш возрастает с

79

ростом глубины памяти, то он уменьшается с ростом числа участников игры. Это и понятно — чем большее число игроков участвуют в игре, тем труднее при про­цедуре общей кассы понять характер зависимости ин­дивидуального выигрыша от индивидуального пове­дения. С этой точки зрения, если метод бригадной оплаты, т. е. общая касса для малой группы, имеет смысл, то реализация того же принципа для большо­го коллектива, например для цеха, выше человече­ских возможностей.