Geum.ru

Варшавский В. И., Поспелов Д. А

Вид материалаДокументы

Содержание


С. Маршака)
Подобный материал:
1   2   3   4   5   6   7   8   9   ...   13
§ 3.5. «Он думает, что я думаю...»

У английского поэта Ковентри Патмора есть та­кие стихи:

— Он целовал Вас, кажется?

— Боюсь, что это так!

— Но как же Вы позволили?

94

— Ax, он такой чудак! Он думал, что уснула я И все во сне стерплю. Иль думал, что я думала, Что думал он: я сплю!

(перевод С. Маршака)

Эти стихи демонстрируют широко распространенную человеческую способность к рефлексии — рас-суждениям, при которых рассуждающий ставит себя на место другого человека и проводит рассуждения с его точки зрения. Рефлексивные рассуждения обла­дают свойством рекурсивности, т. е. как бы вклады­ваются друг в друга, как матрешки. Например, можно рассуждать о том, как некто рассуждает о вас или моделирует ваши рассуждения о нем. Ковентри Пат-мор в своем стихотворении прекрасно иллюстрирует эту рекурсивность рефлексивных рассуждении.

Зачем нам нужны рассуждения подобного типа? Мы их используем тогда, когда делаем выбор, успех и неуспех которого предопределяется не только на­шим собственным решением, но и решениями других людей, связанных с нами какими-то связями. Пример подобной ситуации—игра в размещения, в которой выигрыш каждого участника коллектива определяет­ся не только его индивидуальным действием, но и действиями остальных участников коллектива. По­этому использование в коллективном поведении ме­ханизмов, имитирующих рефлексивные рассуждения, может оказаться полезным. В данном параграфе мы постараемся показать это.

Введем сначала важное для нас понятие ранга рефлексии. Это понятие мы введем индуктивным пу­тем. Будем говорить, что индивид или автомат име­ет нулевой ранг рефлексии, если при выборе своего действия он никак не учитывает наличия других уча­стников коллектива. Выбор при нулевом ранге реф­лексии определяется только той информацией, кото­рая поступила на вход принимающего решение от среды. Индивид (или автомат) имеет первый ранг рефлексии, если он считает, что остальные участники коллектива имеют нулевой ранг рефлексии и он сам может выбирать действия за них. Отметим, что нали­чие первого ранга рефлексии связано с требованием наличия информации по крайней мере о некоторых

95

участниках коллектива и сигналах от среды; поступивших на их вход. Определение последующих ран­гов рефлексии происходит аналогичным образом. Ин­дивид или автомат имеет k-й ранг рефлексии, если он считает, что все остальные известные ему участ­ники коллектива имеют ранг рефлексии, равный k—1, и он может провести за них соответствующие рассуждения.

Т
акое определение ранга рефлексии связано лишь с мерой информированности системы, делающей вы­бор, о сигналах, поступивших на входы других си­стем. У человека же рефлексивные рассуждения в подавляющем большинстве случаев опираются на не­которые знания, хранящиеся в его «модели мира». Это знания о закономерностях поведения в данном обществе, человеческих возможностях в том или ином состоянии, нормах и ограничениях и т. п. Но даже в столь обедненном виде рефлексивные рас­суждения оказываются полез­ными в ряде моделей коллек­тивного поведения.

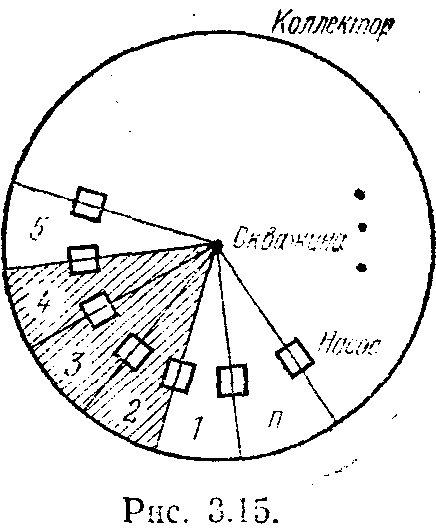
Рассмотрим следующую за­дачу. В дачном кооперативе пробурена скважина для по­дачи воды. На каждом участ­ке имеется свой собственный насос, способный подать воду из скважины в кольцевой коллектор, охватывающий все участки (рис. 3.15). Но мощ­ности этих насосов таковы. что создаваемый ими напор

в коллекторе позволяет производить поливку трех соседних участков, если включены два насоса. Другими словами, если на участках 2 и 3 насосы включены, то можно полить и посадки на участке 4. Каждый хозяин участка имеет индивиду­альную цель — обеспечить свой участок водой. Но имеется еще дачный трест — владелец всех n участ­ков, И у него есть собственная цель — экономия электроэнергии. При обеспечении поливки всех уча­стков для дачного треста невыгодно, чтобы работали все n насосов. Наилучшим для него является случай, когда работает только n/2 насосов (если п—четное), или (n+1)/2 насосов (если п—нечетное). Доста-

96

точно, например, включить насосы лишь на участках с четными (пли нечетными) номерами и весь полив будет обеспечен.

Конечно, дачный трест мог бы добиться этого какими-либо принудительными мерами, например централизованным управлением насосами из цент­ральной диспетчерской. Но владельцы участков это­му противятся, считая, что дачный трест вмешивает­ся в их личные дела. И тогда трест пытается орга­низовать экономию электроэнергии путем денежных штрафов за ненужный расход электроэнергии коллек­тивом владельцев участков.

Прежде чем пояснить, как это делается, отметим некоторую искусственность нашей задачи. Ее содер­жательная интерпретация нужна была нам лишь для того, чтобы вызвать у читателя некоторые образные ассоциации, а не подсовывать ему неизвестно откуда взятую модель, на которой будет показана полез­ность рефлексивных рассуждении.

Перейдем теперь к описанию самой модели. Име­ется кольцо, состоящее из п автоматов (будем для определенности считать п четным). Каждый автомат может находиться в двух состояниях — рабочем и выключенном. Эти состояния мы для краткости бу­дем обозначать соответственно 1 и 0. Каждый авто­мат имеет информацию о своем состоянии и состоя­нии двух своих соседей. Число действий каждого ав­томата также равно двум. Эти действия есть просто сообщения о том, в каком состоянии находится в данный момент автомат. На каждом такте функцио­нирования автоматы получают на вход сигналы поощ­рения и наказания. При поощрении автомат сохраня­ет свое состояние, при наказании — меняет его. Взаимодействие автомата в кольце со средой (дач­ным трестом) определяется табл. 3.3.

Если автомат при выборе своего очередного со­стояния будет руководствоваться только этой табли­цей, то мы будем считать его обладающим нулевым рангом рефлексии. Если все автоматы кольца имеют нулевой ранг рефлексии, то дачный трест может по­пасть в ситуацию, когда достижение его цели окажет­ся невозможным. Если, например, в начальный мо­мент все автоматы находятся в рабочем состоянии, то все они, согласно последней строке таблицы, по­лучат сигнал наказания и перейдут в нерабочие

97

Таблица 3.3
Состояние



Вероятность наказания

собственное
левого соседа
правого соседа



0
0
0
1

0
0
1
0,5

0
1
0
0,5

0
1
1
0

1
0
0
0

1
0
1
0,5

1
1
0
0,5

1
1
1
1


состояния. Но в этом состоянии весь коллектив опять получит сигнал наказания, все автоматы перейдут в рабочее состояние, и цикл замкнется. Насосы на участках будут либо все включаться одновременно, либо бездействовать», а цель дачного треста так и не будет достигнута.

Введем теперь различные ранги рефлексии. Пусть, например, некоторый автомат имеет первый ранг реф­лексии. Тогда он делает свой выбор следующим обра­зом. Он анализирует переход, который должны совер­шить его соседи (а для этого, он должен иметь ин­формацию о соседях своих соседей), считая, что они обладают нулевым рангом рефлексии, т. е. при своем выборе руководствуются приведенной выше таблицей, а затем совершает переход на основании своего рас­суждения. При этом вероятность наказания для него задается уже не средой, а определяется им самим. Другими словами, кроме информации о состояниях, в которых находятся его непосредственные соседи и соседи его соседей, автомат с первым рангом рефлексии должен еще звать правый столбец табл. 3.3, Только при наличии этой дополнительной информа­ции он сможет провести правильное рефлексивное рассуждение. Для иллюстрации его рассмотрим си­туацию, показанную на рис. 3.16. Сначала наш авто­мат проводит рассуждения за левого соседа. Как сле­дует из таблицы, определяющей функционирование автомата с нулевым рангом рефлексии, левый сосед не может получить сигнал наказания и останется в своем состоянии 0. Правый же сосед с вероятностью 0,5 сменит свое состояние и с такой же вероятностью.

98

с
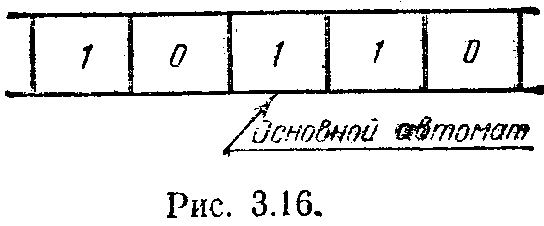
охранит его. Что делать нашему автомату в подобной ситуации? Если правый сосед сменит свое состояние, то, сохранив свое состояние, наш автомат окажется в благоприятном положении. Если же этого на произойдет, то вероятность наказания, которая нависнет над ним, будет равна 0,5. Если же наш автомат сменит свое состояние, то либо он получит сигнал наказания с вероятнос­тью 1 (если правый сосед изменит свое состояние), либо с вероятностью 0,5 (если правый сосед со­хранит свое состояние). В любом случае автомату с первым рангом рефлексии лучше сохранить свое текущее состояние.

Е
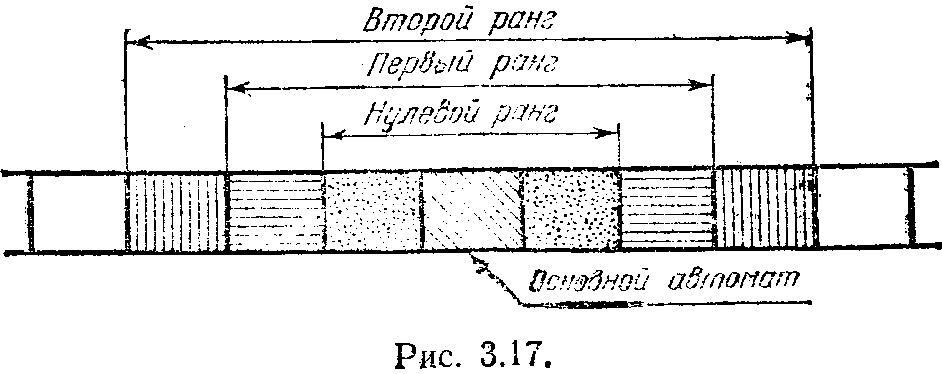
сли бы автомат имел второй ранг рефлексии, то, согласно нашему определению, он считал бы своих соседей автоматами с первым рангом рефлексии, а, значит, проводя рассуждения за них, привлекал бы информацию не только о своих соседях и соседях этих соседей, но и о соседях соседей соседей. На рис. 3.17 показано, как расширяется множество ав­томатов, относительно которых необходимо иметь информацию об их текущих состояниях при росте значения ранга рефлексии.

Отметим, что если некоторый автомат имеет определенный ранг рефлексии, то это вовсе не означает, что он правильно предсказывает реакцию анализируемого множества автоматов. Он может и ошибать­ся. Имея, например, первый ранг рефлексии, автомат предполагает, что его соседи делают свои выборы как автоматы с нулевым рангом рефлексии. Но впол­не может оказаться, что его соседи сами являются

99


автоматами с рангом рефлексии выше нулевого. В этом случае прогноз их поведения не будет соответ­ствовать тому, что они на самом деле будут делать.

Можно поставить следующий вопрос: существуют ли такие распределения значений рангов рефлексии по коллективу автоматов, которые позволяли бы дач­ному тресту надеяться, что со временем коллектив придет к благоприятным состояниям (чередованию состояний 1—0—1—0 и т. д.). Моделирование этой задачи на ЭВМ показало, что коллектив выходит на этот глобальный оптимум не всегда, а лишь при оп­ределенных распределениях рангов рефлексии. Опти­мум по коллективу, например, всегда достигается, когда на кольце чередуются автоматы с нулевым и первым рангами рефлексии. Но он же достигается и не при столь регулярном их чередовании.

В конце § 3.4 мы рассмотрели модель, весьма близкую к той, которую мы сейчас проанализировали. В ней ситуацией равновесия оказывалась партия вида 1010 ... 10 (в обозначениях § 3.4 партия АБАБ ... АБ). Это та партия, которая устраивает нас в задаче включения насосов. Но в ранее рассмотренной мо­дели выход игроков в эту точку обеспечивался за­данной на стр. 94 системой выигрышей. В нашем же случае такой системы выигрышей нет. И коллек­тив автоматов не обладает в этой партии точкой рав­новесия.

Ее возникновение порождается неоднородностью в коллективе автоматов, вносимой различными ранга­ми рефлексии. И эта неоднородность позволяет нам решить задачу оптимизации, которую не способен ре­шить однородный коллектив, если не принять каких-либо дополнительных мер.

§ 3.6. Оптимисты и пессимисты в мире автоматов

Рассмотрим еще один способ введения неоднород­ности в коллектив автоматов, решающий некоторую задачу. Как всегда, начнем с некоторой содержатель­ной интерпретации задачи.

Пусть некто решил жениться. Но поскольку же­нитьба — шаг серьезный, то жених намеревается принять решение только после того, как он будет иметь некоторую информацию о своей будущей спут­нице жизни. Пусть для него жизненно важны две

100

вещи: наличие квартиры у его избранницы и умение ее готовить вкусные обеды. Такой меркантилизм не должен смущать читателя. Авторы книги вовсе не идеализируют героя этой истории, а может быть, и осуждают его за невнимание к вещам куда более серьезным, чем жилплощадь и пища. Но что подела­ешь. Иногда для наглядности приходится мириться с некоторыми недостатками героя примера. Степень информированности жениха об интересующих его предметах будем выражать следующим образом. Если квартира у избранницы есть, то Х1 = 1, в про­тивном случае Х1 = 0. Если же жених пока не обла­дает сведениями о наличии у своей избранницы от­дельной квартиры, то полагаем X1 = 0,5. Аналогично считаем, что умение готовить обеды приводит к Х2 = 1, неумение — к Х2 = 0, а значение Х2 = 0,5 свидетельствует об отсутствии у жениха необходимой информации. Введем еще переменную Y, которая бу­дет отражать решение жениха. Если он твердо решил жениться, то Y=1. Значение Y = 0 свидетельствует об его отказе от избранницы, а Y = 0,5, означает, что жених колеблется, не зная, что ему делать.

Составим отражающую эту ситуацию табл. 3.4. Она задает пять функций троичной логики, завися­щих от двух аргументов X1 и Х2. Наиболее проста из них функция Y1 Как видно из таблицы, Y1=min(X1,X2). В логике такую функцию принято называть конъюнкцией. Если жених использует для принятия своих решений эту функцию, то он согла­шается на брак только при условии выполнения двух своих требований: наличия квартиры и умения гото­вить вкусные обеды. Если хотя бы одно из этих усло­вий не выполнено, то он отказывается от брака. При наличии неопределенности в условиях, когда осталь­ные требования выполнены, или в условиях полной неопределенности (X1 = 0,5; X2 = 0,5) жених медлит с решением и не говорит ни да, ни нет. По-видимому, он ждет новой порции информации. Такое поведение жениха можно назвать объективным или бесстраст­ным.

Остальные функции в нашей таблице описывают способ принятия решений несколько иного типа. Функции Y2 и Yз отражают пессимистическую точку зрения. Жених такого типа всегда предполагает, что мир устроен не лучшим образом и всегда надо ждать

101


Таблица 3.4

X1
X2
Y1
Y2
Y3
Y4
Y5

0
0
0
0
0
0
0

0
0,5
0
0
0
0
0

0
1
0
0
0
0
0

0,5
0
0
0
0
0
0

0,5
0,5
0,5
0
0
0,5
1

0,5
1
0,5
0
0,5
1
1

1
0
0
0
0
0
0

1
0,5
0,5
0
0,5
1
1

1
1
1
1
1
1
1


от него подвоха. Поэтому он склонен интепретировать незнание как отрицательную оценку. Такой же­них — пример явного пессимиста. При этом, если он руководствуется функцией Y2, то его пессимизм до­стигает крайней степени. При наличии любой неопре­деленности происходит отказ от дальнейшего накоп­ления информации, и общение жениха с невестой прекращается. В случае функции Yз пессимизм не столь категоричен. Лишь в случае полной неопреде­ленности жених прекращает свои попытки устроить свою личную жизнь. При частичной неопределенно­сти он стремится продолжить сбор интересующей его информации.

Оставшиеся две функции характеризуют противопо­ложный взгляд на мир. Это взгляд оптимиста, всегда надеющегося, что природа принесет ему неожидан­ную удачу. Оптимист, руководствующийся в своем выборе функцией Y5, представляет собой случай крайнего (пожалуй, даже «оголтелого») оптимиста, ибо в своих рассуждениях он заменяет все оценки 0,5 оценками, равными 1. Функция Y4 характеризует более осторожного оптимиста, который склонен заме­нять единицей не более одной оценки 0,5.

Таким образом, подобно рангам рефлексии можно ввести ранги пессимизма — оптимизма. Будем счи­тать, что бесстрастный жених имеет ранг, равный нулю. Жених, заменяющий т и более оценок 0,5 на 0, имеет ранг пессимизма п—m+1, где п—число, учитываемых условий, а жених, заменяющий т и ме­нее оценок 0,5 на 1,—ранг оптимизма т. В случае двух аргументов, который отражен в нашей таблице,

102

возможны ранги пессимизма и оптимизма 1 и 2. Число возможных рангов растет линейно с ростом числа аргументов n.

При принятии своего решения о браке жених мо­жет руководствоваться и несколько иными соображе­ниями, чем было описано выше. Весьма возможно, что он не такой уж и экстремист и готов жениться и в том случае, когда у его избранницы есть либо квартира, либо она относится к числу хозяек, готовя­щих весьма вкусные обеды. Наличие того и другого одновременно рассматривается таким претендентом на ее руку как редкая удача. Описание процесса принятия решений о браке таким женихом можно представить в виде табл. 3.5.

Таблица 3.5

X1
X2
Z1
Z2
Z3
Z4
Z5

О
0
0
0
0
0
0

0
0,5
0,5
0
0,5
1
1

0
1
1
1
1
1
1

0,5
0
0,5
0
0,5
1
1

0,5
0,5
0,5
0
0,5
0,5
1

0,5
1
1
1
1
1
1

1
0
1
I
1
1
1

1
0,5
1
1
1
1
1

1
1
1
1
1
1
1


Функция Z1=max(X1,Х2) в логике называется дизъюнкцией. Она определяет бесстрастный выбор жениха, согласного на выполнение хотя бы одного своего требования. Функции Z2 и Z3, отражают пес­симистическую точку зрения, a Z4 и Z5 — оптимисти­ческую точку зрения при дизъюнктивном выборе. По­добно тому как при конъюнктивном выборе мы ввели в рассмотрение ранги пессимизма —оптимизма, их можно ввести и при дизъюнктивном выборе. Введен­ные нами функции, кроме Y1 и Z1, можно соответственно называть пессимистическими или оптимистиче­скими квазиконъюнкциями и квазидизъюнкциями тех или иных рангов пессимизма — оптимизма.

Для иллюстрации воздействия введенных нами ха­рактеристик на коллективное поведение автома­тов рассмотрим модель, являющуюся, известным

103


обобщением модели игры в размещения, которая обсуждалась для однородного коллектива автоматов в начале данной главы.

Каждое утро пастух, выгоняющий стадо на выпас, решает довольно сложную оптимизационную задачу:

куда гнать стадо? Он знает п участков, пригодных для выпаса. Но и другие пастухи, пасущие свои стада в том же районе, осведомлены о них не хуже его. И вполне может случиться, что, пригнав свое стадо в прекрасную долину недалеко от деревни, он увидит, что кто-то уже опередил его еще накануне и вся пища уже уничтожена. А в более высокогорной котловине травы может быть совсем немного, ибо дожди в по­следнее время были редки и трава, по всей видимости, не набрала там силу. Есть, правда еще одно прекрасное место, но там почти наверное придется де­лить его с соседями и животным его стада придется съесть меньше, чем они бы смогли.

Как же пастуху добиться своей цели: увеличить живой вес своего стада? Говорят, что в соседнем рай­оне пастухи договорились между собой и составили план выпаса. Но в их районе об этом только погова­ривают. И о чем только думает районное начальство, которое должно заботиться о суммарном весе всего поголовья животных в стадах района?

Оставим на время пастуха с его нелегкими раз­думьями. Формализуем постановку задачи о поиске наиболее благоприятного места для выпаса стада. Вместо пастуха с его стадом будем рассматривать некий автомат, который имеет п различных действий, смысл которых сводится к выбору одного из п участ­ков для выпаса. Каждый такой участок автомат ап­риорно оценивает двумя оценками: оценкой вероят­ности наличия в этом месте достаточного количества пищи для того, чтобы животные не голодали X1i (i здесь номер участка), и оценкой посещаемости уча­стка, отражающей прогноз о среднем числе автома­тов, которые могут одновременно с ним оказаться на участке с номером i(X2i). Эти две оценки могут фор­мироваться за счет накопления некоторого предше­ствующего опыта, знания о характере участков и по­годных условий или на основании «голого эмпириз-ма». Несколько огрубляя задачу, будем считать, что все оценки имеют троичный характер. Тогда X1i=1

104

означает, что на участке i имеется достаточно пищи для прокорма стада, X1i=" 0 — что пищи на участке i явно мало, a X1i==0,5 — что у автомата нет информации о вероятности нахождения на участке i достаточ­ного количества пищи. Вторые оценки имеют следующий смысл: X2i== 1 — на участке с номером i предполагается такое количество одновременно пасущихся автоматов, которое при равном распределении ресур­сов (пропорционально числу пасущихся автоматов, пришедших на этот участок) обеспечивает нашему автомату необходимое количество пищи; X2i==0 озна­чает, что пищи при дележе с соседями по участку будет явно недостаточно, а X2i==0,5 свидетельствует об отсутствии информации по этому вопросу.

Таким образом, при принятии решения о выборе участка автомат может действовать как наш гипоте­тический жених, принимающий решение о браке. Что же показали результаты моделирования на ЭВМ? Коллектив автоматов выходил на оптимум с точки зрения районного начальства лишь при определенных распределениях рангов пессимизма — оптимизма. При этом, если в модели допускалось «вымирание» автоматов — т. е. они в течение некоторого числа тактов распределений по участкам не набирали по­рогового значения количества пищи, то с течением времени моделирования в коллективе возрастал про­цент умеренных пессимистов, которые оказывались более жизнеспособными, чем оптимисты всех рангов. Процентный состав пессимистов и оптимистов в кол­лективе, распределение их по рангам во многом за­висят от истинных параметров среды. Но в любом случае крайние пессимисты и оптимисты приносят мало пользы коллективу и при наличии вымирания быстро из него исчезают. Наиболее устойчивыми в среднем оказываются совокупности, в которых около 40 % бесстрастных автоматов, около 40 % умеренных пессимистов и 20 % умеренных оптимистов.

Этот феномен связан с тем, что в однородных кол­лективах без организации какого-либо взаимодей­ствия между автоматами (например, общей кассы или случайного парного взаимодействия) все автоматы кучно переходят от одного выбора к дру­гому. Если же в коллективе имеются различные автоматы, то пессимисты и оптимисты выбирают те

105


участки, которые не выбрали бы бесстрастные автоматы, что приводит к «размазыванию» коллектива автоматов по участкам. Тот же эффект, как было показано, достигается введением общей кассы в од­нородном коллективе автоматов, решающем задачу размещения.

В рассмотренной нами модели «игроки» оперировали не с самими значениями тех или иных параметров среды, а с их оценками. В одном из эксперимен­тов, например, предлагалось, что X1i==1, если вероят­ность наличия нужного количества пищи на участке с номером i больше 0,75. Если она была меньше 0,25, то полагалось, что X1i=0. В остальных случаях принималось, что X1i=0,5. Для второго параметра X2i=1> если на i-м участке было менее 1/4 всех стад, имеющихся в районе. А когда это количество увеличивалось до 3/4 или превосходило это число, полагалось, что X2i=0. В остальных случаях оценка второго параметра была равна 0,5. Субъективизм. этих границ очевиден. Люди в своей практике при­нятия решения в конфликтных ситуациях используют многие виды таких субъективных оценок.

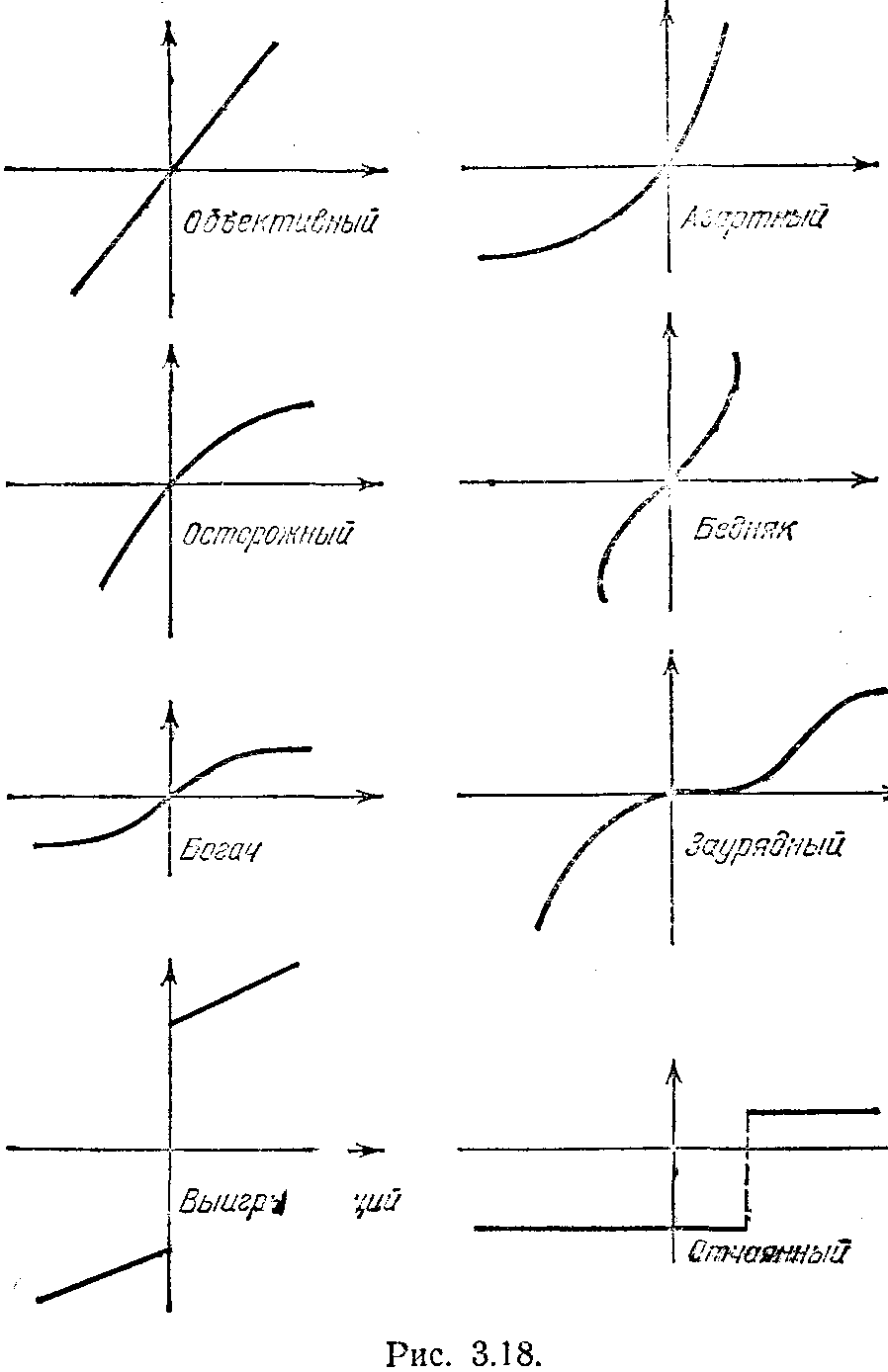
На рис. 3.18 показаны кривые, характеризующие отношения игрока-человека к получаемым им в про­цессе игры выигрышам. По оси абсцисс на графиках отложены величины выигрыша — проигрыша игроков, а по оси ординат—субъективные оценки этих значений игроком. Названия, приведенные на рисун­ке, говорят сами за себя. Дж. Кемени и Дж. Томпсон, проанализировав эти функции оценок, показали, что в коллективе из игроков с различной психологи­ческой доминантой решения, принимаемые ими в одних и тех же условиях, могут быть весьма различными. Приведем одну из моделей, предложенную ими.

Пусть некто устраивает лотерею. Он выбирает такую стоимость одного лотерейного билета s, при­обретя который участник лотереи может с вероят­ностью g выиграть некоторую сумму l. Математиче­ское ожидание проигрыша для устроителя лотерея равно g{-l)+(l-g)s. Конечно, он не захочет про­игрывать и сделает так, чтобы выполнялось неравен­ство 0

106

В

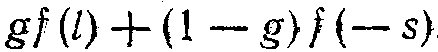
еличина g мала, так как l велико по сравнению с s. Пусть человек, купивший лотерейный билет, оцени­вает свои выигрыши и проигрыши с помощью одной из тех оценочных функций f, которые показаны на рис. 3.18. Тогда он оценивает математическое ожидание полезности покупки лотерейного билета как


Естественно считать, что человек покупает лоте-рейный билет только в том случае, когда эта оценка положительна. Тогда разные типы игроков примут

107

различные решения. Легко представить себе, что при определенных значениях s, l и g их решения распре­делятся следующим образом: решение играть примут азартный игрок и бедняк; заурядный игрок будет играть в лотерею лишь при малых значениях l, а от­чаянный при l, большем, чем абсцисса точки раз­рыва; объективный, осторожный, выигрывающий и богач откажутся от участия в лотерее; заурядный откажется при больших значениях l, а отчаянный — если l меньше абсциссы точки разрыва на графике его оценочной функции.

Материал двух последних параграфов свидетель­ствует о том, что в моделях коллективного поведения введение неоднородности служит тем же целям, что и дополнительные механизмы по целенаправленному воздействию среды на участников коллектива. Поэто­му можно считать, что разнородность, столь часто встречающаяся в природе и технических системах, не является чем-то случайным, «нарушающем гармо­нию», а отражает фундаментальную идею о лучшем функционировании разнородных коллективов, решаю­щих общую задачу в условиях децентрализации, по сравнению с однородными коллективами, решающи­ми ту же задачу.