Варшавский В. И., Поспелов Д. А

Вид материала

Документы

Подобный материал:

• Герберт Александер Саймон Исследователи ии: Лотфи Заде Исследователи ии: А. А ляпунов,, 9.34kb.
• «Как привлечь средства государственных институтов развития» Варшавский Владислав Римович, 48.54kb.
• Аннотация к научно-образовательному материалу, 114.81kb.
• 141. Поспелов В. И., Стальнов В. С. Содружественная аккомодация глаз при дисбинокулярной, 167.36kb.
• Тезисы докладов участников III международного конгресса «Россия и Польша: память империй, 1372.37kb.
• Д. А. Поспелов, Г. С. Осипов, 487.33kb.
• Варшавский А. С. Следы на дне, 1828.32kb.
• Рабочая программа учебной дисциплины Для направления 080100. 62 «Экономика» (программа, 562.39kb.
• Диспут с Пирром: прп. Максим Исповедник и христологические споры VII столетия / Отв, 73.89kb.
• Программа дисциплины: Имитационные модели для направления Прикладная математика и информатика, 120.53kb.

§ 3.3. Распределение ограниченного ресурса

Каждый раз, говоря о коллективном поведении, мы имеем ввиду коллективное поведение объектов в некой системе. При организации такого поведения нас интересует, безусловно, достижение определенных си­стемных целей, удовлетворение общесистемных кри­териев качества функционирования. При этом (и здесь основной смысл организации децентрализо­ванного управления) отдельный объект не имеет ин­формации об общих целях системы. Объект знает только свои локальные цели, локальные критерии, локальные функции предпочтения. Управление систе­мой организуется путем формирования таких локаль­ных условий и, быть может, таких правил локального взаимодействия, при которых удовлетворение локаль­ных интересов отдельных объектов, составляющих систему, приводило бы к удовлетворению общеси­стемных целей. И здесь возникает естествен­ный вопрос о том, что же является тем объ­ектом в системе, локальное поведение которого мы организуем.

В предыдущих параграфах данной главы мы рас­смотрели две игры — игру в размещения и игру в распределения (игру Гура). В обеих играх эффек­тивность функционирования системы зависела от рас­пределения ограниченного числа участников игры по стратегиям. В качестве примера мы говорили о рас­пределении трудового ресурса по местам работы. Ресурсом в этих задачах могли служить объекты са­мой различной природы, например, задания, вы­полняемые в многопроцессорной вычислительной система. Существенным здесь было то, что мы

80

«персонифицировали» типы ресурса- и занимались организацией их коллективного поведения.

Вместе с тем, в качестве объектов, составляющих систему, можно рассматривать и потребителей ресурса. Тогда нас будет интересовать проблема организа­ции их совместного поведения, обеспечивающего оп­тимизацию общесистемного эффекта использования ресурса.

З
адача об оптимальном распределении ресурса между потребителями имеет смысл только тогда, когда этот ресурс ограничен. В качестве ресурса мо­гут выступать самые различные объекты: деньги, энергия, сырье, машины ч т. п. Существенно здесь то обстоятельство, что каждый потребитель, используя некоторое количество ресурса, добивается определен­ного эффекта. Для того чтобы задача о распределе­нии ресурса имела смысл, необходимо также, чтобы в пределах всей системы эти эффекты были соизме­римы. Поиск такой общей меры является самостоя­тельной задачей и в ряде случаев (если не в боль­шинстве), не привносится в систему «сверху», а так­же порождается совмест­ным функционированием подсистем. Здесь, однако, мы будем предполагать, что такая мера существует.

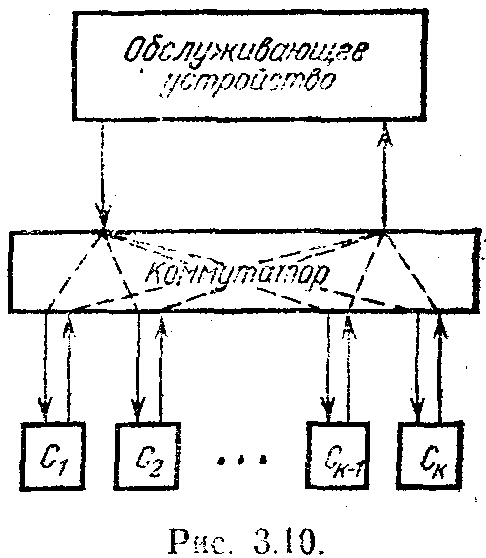
Рассмотрим несколько примеров. Пусть у нас име­ется система, состоящая из k объектов и одного обслу­живающего устройства (рис. 3.10). Обслуживающее ус­тройство периодически с периодом длительности Т через коммутатор подклю­чается к каждому обслу­живаемому объекту и работает с ним в течение

времени t_k. При этом очевидно, что Сумма( t_k )=Т. Дли­тельность периода Т выступает здесь в качестве огра­ниченного ресурса, распределяемого между объекта­ми обслуживания. На каждом объекте в результате обслуживания его в течение времени t_k достигается эффект, равный Фи_k(t_k). Заметим опять, что все эф­фекты соизмеримы, т. е. измерены в одних и тех же

81


единицах. При этом могут существовать различные системные критерии качества функционирования.

Предположим, что в качестве объектов выступают следящие устройства с импульсным регулированием через один и тот же регулятор (обслуживающее устройство). Качество функционирования каждого сле­дящего устройства, зависящее при заданном периоде от скважности сигналов регулятора, определяется, например, среднеквадратичным отклонением от от­слеживаемой величины. Поведение системы опреде­ляется среднеквадратичным отклонением наихудшего устройства. В этом случае наилучшее поведение си­стемы получается при достижении min max Фи_k(t_k). Нетрудно понять, что этот критерий удовлетворяется в том случае, когда среднеквадратичные ошибки во всех устройствах одинаковы. Действительно, если при определенном распределении времен обслужива­ния в течение периода в одном из каналов слежения ошибка больше, чем в других, то имеет смысл увели­чить время обслуживания этого следящего устрой­ства путем некоторого увеличения ошибки в других каналах. Здесь мы исключаем из рассмотрения такие экзотические случаи, когда распределение времен об­служивания, обеспечивающее равные ошибки во всех следящих устройствах, вообще недостижимо. Для это­го. достаточно предположить, что ошибки в этих уст­ройствах монотонно уменьшаются при уменьшении скважности регулирования. Оптимальное распределе­ние ресурса в таком случае определяется решением системы уравнений

Фи_k(t_k) - Лямбда = 0, (k=1, k); Сумма (t_k) = T.

В качестве общесистемного критерия может выступать и просто арифметическая сумма эффектов, которые возникают у потребителей ресурса, как, на­пример, было с лесозаготовительными участками в приведенном выше примере (см. § 3.2). В системе, структура которой изображена на рис. 3.10, такой эффект функционирования системы может опреде­ляться суммарным достигаемым эффектом и поведени­ем системы, обеспечивающем приближение к Сумма[Фи_k(t_k)]. В этом случае, как следует из теории нелинейного программирования, оптимальное распределение до­стигается в ситуации,. определяемой решением систе-

82

м
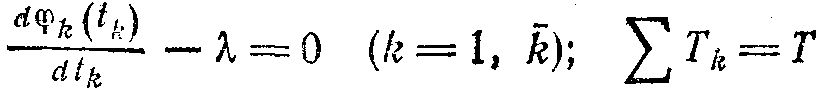
ы уравнений


где К имеет смысл цены на единицу используемого ресурса. В дальнейшем мы ограничимся ука­занными двумя типами задачи о распределении ресурса, хотя могут рассматриваться весьма разнооб­разные ее постановки. Например, имеет самостоятель­ный интерес задача о минимизации общего количе­ства используемого ресурса при фиксированной сум­ме эффектов, достигаемых потребителями ресурса.

Как мы уже говорили, нас в задаче о распределе­нии ресурса интересует организация коллективного поведения в условиях децентрализации, обеспечиваю­щая решение, состоящее в удовлетворении общеси­стемного критерия функционирования. В этом пара­графе мы займемся рассмотрением организации кол­лективного поведения потребителей ресурса.

При такой организации поведения мы, однако, не можем исключить из рассмотрения еще одного участ­ника — владельца ресурса. О какой же децентрализа­ции может идти речь при наличии центрального объекта, который располагает ресурсом и раздает его потребителям?

З
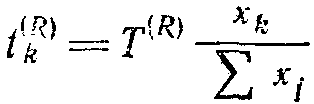
аметим, что мы рассматриваем децентрализацию. поведения при оптимизации и, следовательно, ресур-содержатель не должен решать никаких оптимизаци­онных задач. Более того, мы будем стремиться к то­му, чтобы обмен информацией в системе был доста­точно простым, например, сводился бы к тому, чтобы потребители ресурса посылали в центр заявку на же­лательное количество ресурса, а центр достаточно простым способом на основании полученных заявок делил бы его между потребителями. Наиболее про­стой способ такого распределения—распределение всего ресурса пропорционально поступившим заяв­кам. Тогда, если х_k — количество указанного в заяв­ке k-го потребителя ресурса, то количество выделяе­мого ему ресурса равно


Теперь возникает естественный вопрос — существуют ли локальные правила формирования заявок на

83


ресурс при описанном способе его распределения, обеспечивающие оптимизацию поведения системы по общесистемному критерию?

Р
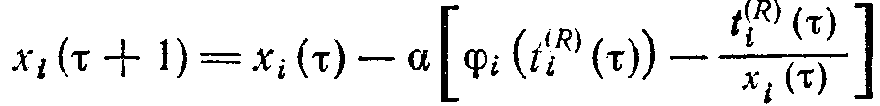
ассмотрим задачу с минимаксным критерием. Допустим вначале, что центральное устройство на­значает величину л и сообщает ее всем потребителям ресурса, а потребители ресурса указывают свои за­явки на ресурс так, чтобы сделать получаемый ло­кальный эффект равным Лямбда. Тогда, если у потребителя эффект меньше Лямбда, он увеличивает заявку, а если больше — уменьшает ее. Если все потребители уменьшают свои заявки, то это означает, что Лямбда мень­ше, чем необходимо, а если увеличивают, то Лямбда боль­ше, чем необходимо. В связи с этим центр ведет себя следующим образом: уменьшает Лямбда, если сумма заявок меньше наличного количества ресурса, и увеличива­ет Лямюда, если наличное количество ресурса меньше сум­мы заявок на него. В ситуации, когда все эффекты равны Лямбда и сумма запрошенного ресурса равна налич­ному его количеству, система находится в устойчивом равновесии. Заметим, однако, что мы нарушили анон­сированный выше принцип — центральное устройство занимается регулированием значения Лямбда. Кроме того, центральное устройство должно сообщать потреби­телям текущее значение Лямбда. С другой стороны, если весь ресурс распределяется пропорционально подан­ным заявкам, то количество выделяемого потребите­лю ресурса несет информацию о соотношении суммы запросов и наличного запаса ресурса. Этой информа­цией можно воспользоваться и находить свои запро­сы на шаге (Тау + 1) следующим образом:


П
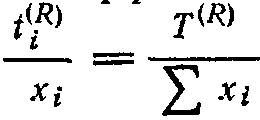
ри этом ситуацией равновесия будет ситуация, в ко­торой весь ресурс распределяется между потребите­лями и достигаемые эффекты у всех потребителей одинаковы и равны

Коэффициент Альфа определяет «чувствительность» потребителя, т. е. степень его инерционности. В этом смысле он некоторым образом аналогичен глубине Памяти автоматов в рассмотренных выше моделях поведения. Точность достижения оптимума растет с

84

уменьшением Альфа, но при этом падает способность опе­ративно реагировать на изменение условий функцио­нирования.

Мы уже отмечали выше, что в случае максимиза­ции суммарного эффекта от распределения ресурса, Лямбда имеет содержательный смысл цены единицы ресур­са и условие системного максимума выполняется то­гда, когда достигают максимума локальные функции пользы, представляющие собой разность между эф­фектом от использования ресурса и стоимостью по­следнего. При этом количество запрашиваемого ре­сурса мы можем интерпретировать, как некую сумму денег, направляемую в центр для его приобретения. Осуществив распределение ресурса между потребите­лями пропорционально присланным деньгам, центр тем самым устанавливает и цену единицы ресурса, равную отношению общей суммы присланных денег к числу распределенных единиц ресурса. Таким обра­зом, количество запрашиваемого ресурса выражается в стоимости полученного ресурса. Тогда общесистем­ный критерий удовлетворяется, если каждый потре­битель формирует свой запрос так, чтобы максими­зировать разность между достигнутым от использо­вания ресурса эффектом и посылаемой заявкой на ресурс. При этом в принципе безразлично, какие алго­ритмы и какие вычислительные средства применяет потребитель для поиска своего локального экстрему­ма. Важно, что мы сформулировали простые и одно­значные правила поведения центра и локальные кри­терии, следование которым обеспечивает децентрали­зованный поиск общесистемного экстремума.

Демонстрация таких возможностей и была целью настоящего параграфа.

§ 3.4. Что дает случайное взаимодействие

Во всех рассмотренных в данной главе моделях участник игры воспринимал результат поведения ос­тальных участников только как реакцию на его по­ведение некоторой более или менее сложно организо­ванной внешней среды. Никакой информацией не только о поведении, но даже о наличии других участ­ников автомат (или игрок) не располагал. Как было показано выше, в ряде ситуаций в дополнительной информации не было никакой необходимости, так как

85


и без нее автоматы добивались целесообразного и даже оптимального поведения. Вместе с тем мы стал­кивались и с рядом не очень приятных характери­стик поведения — требования роста сложно­сти процедуры принятия решений (глубины памяти автоматов), весьма быстрого роста времени достиже­ния оптимального поведения и т. п. И вообще термин «коллективное поведение» мало подходил к описы­ваемым ситуациям — речь скорее всего шла о моделях совокупного поведения, о поведении некоторого «автоматного газа». Когда мы произносим слово «коллектив», мы обычно подразумеваем некоторую структуру отношений, наличие обмена информацией, организацию взаимодействия между членами коллектива. Можно надеяться, что учет указанных свойств в рассматриваемых нами совокупностях автоматов может, с одной стороны, улучшить характеристики поведения и, с другой, оценить возможности и эффек­тивность различных типов организации взаимодей­ствия.

При попытках построить модели поведения со взаимодействием следует постоянно помнить, что только достаточно простые модели, зависящие от не­большого числа параметров, позволяет разобраться в эффектах, возникающих в этих моделях и моделируе­мых ими ситуациях.

Какие же типы взаимодействия мы можем отне­сти к простейшим? К таким типам с нашей точки зрения следует отнести случайное парное взаимодей­ствие и однородное взаимодействие с ограниченным числом соседей.

Случайное парное взаимодействие состоит в том, что в каждый момент времени (в каждой партии иг­ры) весь коллектив, вся совокупность автоматов случайным образом разбивается на пары. Б каждой паре может быть реализован акт обмена информацией, в результате которого происходит изменение действия или внутреннего состояния автомата. На следующем такте разбиение коллектива на пары происходит за­ново, также случайным и независимым от предыду­щего разбиения способом.

При взаимодействии с ограниченным числом сосе­дей для каждого члена коллектива указывается его окрестность — список участников игры, называемых соседями данного автомата по игре, с которыми он

86

может осуществлять взаимодействие. Взаимодействие это может быть односторонним — автомат восприни­мает информацию от своих соседей ко игре или его выигрыш зависит от поведения его соседей по игре, но обратное в общем случае может быть неверным. Однородность ограниченного взаимодействия заклю­чается в том, что размеры окрестности для всех автоматов одинаковы. Таким образом, однородное взаимодействие задается однородным ориентирован­ным графом отношений.

Начнем изучение возможностей взаимодействия со случайных парных встреч.

При рассмотрении игры в размещения мы уже отмечали, что для обеспечения возможности догово­риться и, тем самым, обеспечить максимально возможный выигрыш можно организовать общую кассу, а можно, распределившись по одному на самых вы­годных участках, например циклически меняться ме­стами. Аналогичного эффекта нетрудно добиться, если повторять жеребьевку, например, каждый месяц. Однако трудности организации ежемесячных встреч не привыкших к дисциплине детей лейтенанта Шмид­та отчетливо демонстрируют все сложности такого способа централизованного управления. Столь же большие трудности (если не большие) встречаются на пути заочной жеребьевки и организации общей кассы. Однако эффект, эквивалентный эффекту вве­дения общей кассы, мог бы быть достигнут, если бы в конвенцию был включен пункт, обязывающий от­прысков героя при любой случайной встрече обмени­ваться участками. Если такие парные встречи дейст­вительно случайны и равновероятны, то механизм подобного взаимодействия обеспечивает каждому уча­стнику (естественно, при достаточном времени) пре­бывание в среднем одинаковое время на каждом уча­стке, т. е. выравнивает доходы всех участников игры. Для максимизации выигрыша при этом достаточно обеспечить первоначальное распределение всех игро­ков по одному на наиболее выгодных стратегиях и реализовать процедуру случайного парного обмена стратегиями.

Нетрудно видеть, что и в игре в распределения, если мы зададим некоторое начальное распределение игроков по стратегиям и организуем случайный пар­ный обмен стратегиями (первый тип взаимодействия).

87


то начальное распределение будет поддерживаться сколь угодно долго, так как при парном обме­не, порожденным любым механизмом разбиения на пары, число игроков, покидающих стратегию, будет равно числу игроков, выбирающих ее. С другой сто­роны, если разбиение на нары случайно и равнове­роятно, то средний выигрыш у игроков выравнивает­ся. Указанные соображения позволяют предположить, что таким образом организованная процедура взаимо­действия должна приводить к эффектам, эквивалент­ным введению общей кассы. Здесь, однако, представ­ляет интерес зависимость поведения автоматов в эк­вивалентной игре от глубины их памяти.

Обратимся снова к игре в распределения. Если автоматы, участвующие в игре, имеют минимальную глубину памяти, то указанное взаимодействие не из­меняет их поведения и, следовательно, автоматы ра­зыгрывают партию Антоса. С ростом глубины памя­ти таких автоматов их поведение стремится к пове­дению в игре с общей кассой, а разыгрываемая пар­тия — к партии Мора. Наиболее существенный эф­фект, возникающий здесь, как показывает анализ и моделирование поведения, состоит в том, что при данном типе взаимодействия и при любой глубине памяти средний выигрыш автоматов не меньше, чем максимальный выигрыш для данной глубины памяти в обычной игре и игре с общей кассой.

Первый тип взаимодействия, улучшая результаты поведения автоматов в игре и реализуя процедуру общей кассы без специального центрального устрой­ства, собирающего все выигрыши и делящего их по­ровну между игроками, не улучшает между тем ди­намики поведения коллектива. Сходимость к точке Мора остается столь же медленной.

Мы уже говорили выше, что в игре Гура чрезвы­чайно медленная сходимость объясняется тем, что при любой глубине памяти точкой динамического рав­новесия является точка, при которой автоматы рав­номерно распределены по стратегиям. Более того, в любой другой партии опять-таки при любой глубине памяти математическое ожидание изменения распре­деления автоматов по стратегиям направлено в сто­рону точки равномерного распределения. Можно предложить сравнительно простую процедуру случай­ного парного взаимодействия (взаимодействие второ-

88

го типа), которая делает все партии игры Гура пар­тиями безразличного равновесия по математическому ожиданию смены распределения автоматов по стра­тегиям. Тогда опять средний выигрыш будет опреде­ляться временами выбора автоматом данной страте­гии.

Подобное взаимодействие, обеспечивающее опи­санный выше эффект, состоит в том, что когда авто­мат должен изменить свое действие в качестве ново­го выбирается действие, которое осуществляет парт­нер по паре. Если же в силу логики своей работы, автомат не должен изменять свое действие, то он не обращает никакого внимания на своего партнера по паре.

Эффект, достигаемый при этом типе случайного парного взаимодействия, оказывается замечательным. Если участвующие в игре автоматы имеют глубину памяти, равную п, то их средний выигрыш будет ра­вен выигрышу автоматов, имеющих глубину памяти 2ⁿ, в игре Гура без случайного парного взаимодей­ствия, а скорость сходимости к стационарному выиг­рышу будет такой же, как у автоматов с памятью п в обычной игре Гура. Заметим, что два связанных друг с другом автомата, каждый из которых имеет п состояний, образуют систему с n² состояниями. Учитывая, что такая пара автоматов имеет четыре, а не две комбинации выигрыша и проигрыша, мы можем утверждать, что образование постоянных каолиций из автоматов дает степенное улучшение качества функционирования, тогда как случайное парное взаи­модействие обеспечивает экспоненциальное улучше­ние.

Совместное использование обоих типов случайного парного взаимодействия в игре в распределения обеспечивает проявление обоих указанных выше эф­фектов при достаточно большой глубине памяти. Од­нако введение второго типа случайного парного взаимодействия изменяет характер поведения в этой игре простейших автоматов.

Рассмотрим следующую ситуацию, моделируемую игрой в распределения. Пусть имеется несколько курортов. Привлекательность каждого курорта для отдыхающего там человека зависит от числа людей, выбирающих этот курорт одновременно с ним. Обыч­но в среднем привлекательность курорта падает по


мере роста числа находящихся там курортников. Падение привлекательности курорта приводит к тому, что возрастает вероятность в будущем году поехать в новое место. Каждый из нас знает, как мучитель­на смена привычного места и сколь случайна процеду­ра выбора нового. Однако, как правило, мы не бро­саем монету и не тычем с закрытыми глазами пальцем в карту СССР, а начинаем интересоваться, где отдыхают другие люди. Окончательное решение приходит, когда жена сообщает вам, что Эльвира Евсеевна прекрасно провела лето под Мариуполем. Самое удивительное при этом, что, в общем, с учетом са­мых различных факторов, удовлетворенность провес денным отпуском в среднем во всех местах одинако­ва. Это наводит на мысль, что указанная процедура обеспечивает выход на точку Нзша, а способ выбора нового места весьма напоминает последний способ организации случайного парного взаимодействия.

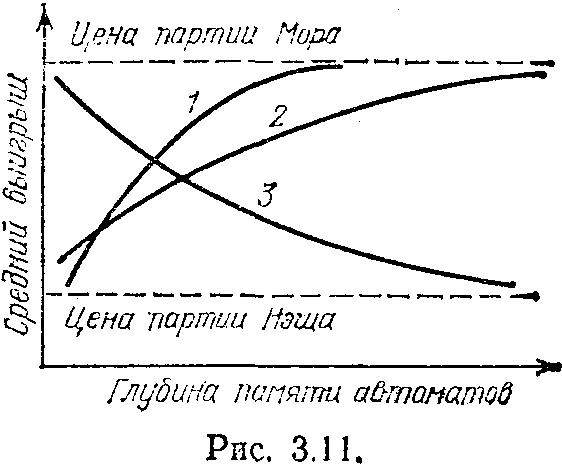
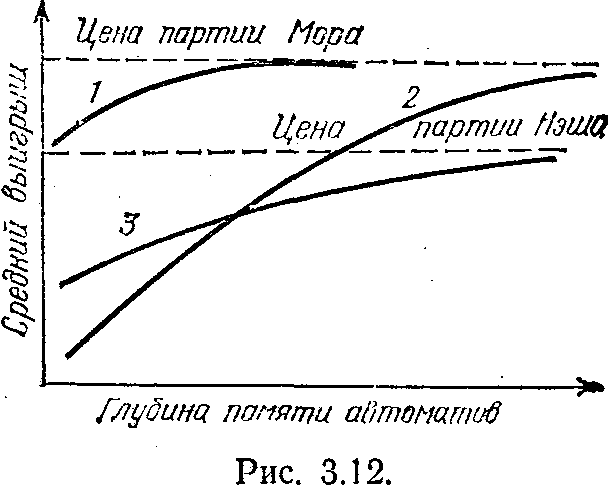
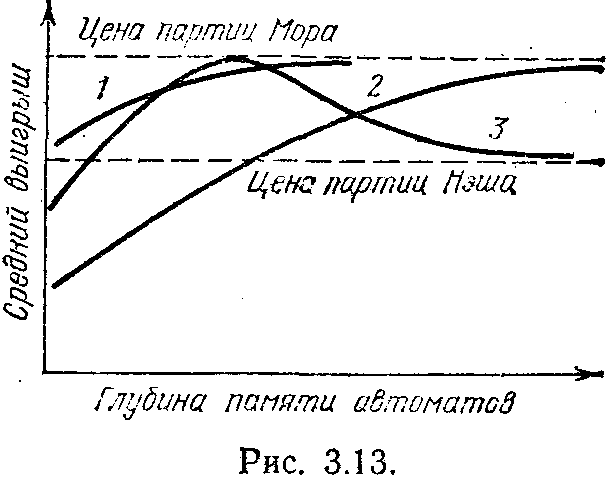
Действительно, если читатель согласен не забивать себе голову аналитическими выкладками и готов поверить нам на слово, то оказывается, что в «игре в распределения» случайное парное взаимодействие, состоящее в том, что в случае смены действия в каче­стве нового действия выбирается действие партнера по паре, обеспечивает выход простейших автоматов на партию Нэша. Этот факт также замечателен, тах как без взаимодействия для обеспечения выхода на точку Нэша необходимы автоматы с бесконечно боль­шой глубиной памяти. Резкое снижение требуемого объема памяти играющих автоматов столь же суще­ственно снижает время, необходимое для выхода на стационарное распределение, и значительно улучшает характеристики поведения в случае изменения внеш­них условий. На рис. 3.11, 3.12 и 3.13 (на них 1 — случайное парное взаимодействие, 2—общая касса, 3—обычная игра) приведены зависимости среднего выигрыша автоматов от глубины их памяти при ком­бинированном способе случайного парного взаимодей­ствия для игр, рассмотренных на рис. 3.7, 3.8 и 3.9.

В

структурированных коллективах, т. е. в коллек­тивах, для которых определена структура взаимодей­ствия, эффективность функционирования каждого участника зависит от того, что он делает сам и что делают его непосредственные соседи по игре. Подоб­ная ситуация возникает, например, тогда, когда чле­ны коллектива располагаются в узлах некоторой сети связи или сети распределения некоторого ресурса, Примерами подобных ситуаций могут слу­жить сети связи или сети вычислительных машин, где мы хотим организовать децентра­лизованное поведение, оптимизирующее неко­торые параметры си­стемы. В качестве та­ких параметров могут выступать производи­тельность или пропуск­ная способность, ре­активность системы или среднее время ожидания, стоимость и т. п. Децентрализо­ванное поведение при решении задач такого рода мы будем рас­сматривать в следую­щей главе. Здесь же нас будут интересовать не­которые эффекты, свя­занные собственно со взаимодействием, по­рождаемым структурой связей в системе. Вве­денные выше требо­вания ограниченности взаимодействия и его однородности вызва­ны следующими при­чинами: ограничен­ность связана с тем, что в большинстве ре­альных технических сетей узлы сети имеют ог­раниченное число связей друг с другом, а однород­ность (так же, как и ограниченность) существенно упрощает изучение моделей.

В
качестве примеров управляющих систем с сетевой структурой могут выступать также системы

91

управления энергетическими или газораспределитель­ными сетями.

Мы будем говорить, что на однородном графе за­дана однородная игра с ограниченным взаимодейст­вием, если задана функция, определяющая доход иг­рока в зависимости от того, какое действие выбрал он сам и какие действия выбрали его соседи по игре. Естественно, что эта функция может зависеть и от внешних неконтролируемых участниками игры пара­метров. В силу однородности графа взаимодействия для задания игры достаточно задать всего одну та­кую функцию.

Рассмотрим некоторую условную ситуацию. Пусть у нас имеется водопроводная сеть, состоящая из рас­пределительных станций, соединенных между собой водоводами. Станция регулирует отпуск воды потре­бителям. Ее доход, с одной стороны, растет с увели­чением общего объема отпускаемой потребителям воды, но, с другой стороны, увеличение этого объема может привести к падению давления в магистралях, что вызовет определенные убытки и, следовательно, снижение дохода. При этом указанные зависимости определяются не только поведением самой станции, но и отбором воды из системы, осуществляемым бли­жайшими соседями станции. Аналогичные отношения возникают и в оросительных системах.

Приведенная содержательная интерпретация мо­дели игры с ограниченным взаимодействием весьма и весьма приблизительно описывает реальную ситуа­цию в подобных системах, но авторы надеются на снисходительность читателя. В принципе функции выигрыша могут учитывать все сложности оценки эффективности функционирования узла. Например, отказ станции включать насосы, обеспечивающий экономию электроэнергии. Существенно здесь лишь то обстоятельство, что доход каждого участника оп­ределяется только поведением его самого и его соседей из ближайшей окрестности.

В
такой игре существуют устойчивые по Нэшу ситуации, когда никому из участников игры невыгод­но в одиночку изменять свое поведение. Аналогично рассмотренным выше играм, доход в точке Нэша всей системы может быть весьма далек от возможно­го максимума. Для достижения партии максимальной цены можно организовать общую кассу, однако не-

93

трудно понять, что в достаточно больших сетях ее введение практически лишает участников оператив­ной информации о реакции системы на их собствен­ное поведение. Вместе с тем, именно с ростом сети возрастают сложности централизованного управле­ния и увеличивается привлека­тельность децентрализованных систем.

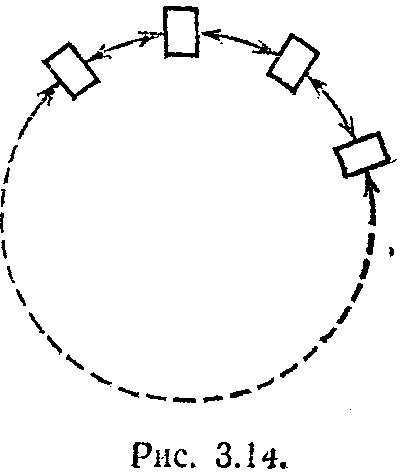
Рассмотрим простенький чис­ленный пример. Пусть участни­ки игры имеют по два соседа каждый, т. е. их графом взаимо­действия является окружность (рис; 3.14). Выигрыш каждого участника определяется его дей­ствием и действиями его правого и левого соседей. Каждый уча­стник может делать одно из двух действий, которые мы обозначим через А и Б. Величины выигрыша автомата в зависимости от дей­ствий его правого и левого соседей приведены ниже

Ситуация Выигрыш

ААА — 2

БАА 2

АБА 0

ББА 10

ААБ 10

БАБ 0

АББ 2

БББ —2

Отсюда видно, что среднему игроку выгодно изме­нять свое действие на другое, если он находится в си­туациях ААА, БАА, АББ и БББ, и невыгодно в ос­тальных ситуациях. Рассмотрим ситуацию ББАА, в которой третьему игроку выгодно изменить свое дей­ствие, что приводит нас к конфигурации БББА, в ко­торой становится выгодным изменить свое действие второму игроку. Ситуацией равновесия по Нэшу здесь является партия АБАБАБ ... АБ. Средний выигрыш в партии Нэша для этой игры равен 0. С другой сто­роны, партия ААББААББ ... ААББ обеспечивает средний выигрыш, равный 6, но, как мы видели, она неустойчива.

Обратим внимание на следующий факт: если один из участников игры изменяет свое действие, то это приводит к изменению только его выигрыша и выиг­рыша его ближайших соседей, но не затрагивает ос­тальных участников игры. Следовательно, если мы организуем общие кассы между соседями по игре, то изменение своего действия, приводящее к уменьше­

93


нию суммарного выигрыша в своей окрестности, а, значит, и во всем коллективе, становится для участ­ника невыгодным. Тогда и партия максимальной цены становится устойчивой по Нэшу, т. е. становится Таблица 3.2

Фрагмент партии Мора	Выигрыш	Фрагмент новой партии	Выигрыш
ААББА	22/3	АААБА	8/3
АББАА	14/3	АБААА	0
ББААБ	22/3	БББАБ	8/3
БААББ	14/3	БАБББ	0

партией Мора. Проиллюстрируем сказанное на нашем примере. Обратимся к табл. 3.2. В ней в первом столбце приведены фрагменты партии максимальной цены, во втором столбце — выигрыш среднего во фрагменте игрока при наличии локальной общей кас­сы, в третьем столбце—фрагмент, образующийся при смене действия средним игроком, и, в четвер­том — выигрыш среднего во фрагменте игрока при наличии локальной общей кассы в новой ситуации.

Из табл. 3.2 видно, что ни одному из участников игры при использовании процедуры локальной общей кассы в партии максимальной цены невыгодно изме­нять свое действие.

Организация локальной общей кассы сводится к равномерному распределению дохода в узле между всеми узлами его окрестности и, с одной стороны, не требует сложных организационных мероприятий, а с другой, в силу небольшого числа соседей слабо мас­кирует зависимость получаемого дохода от результатов собственной деятельности. Еще раз подчеркнем, что указанный эффект достигается на сети независи­мо от ее размеров.