Варшавский В. И., Поспелов Д. А

Вид материала

Документы

Содержание Ai поступает входной сигнал Xi Во справа на младший разряд множителя. Этот сигнал как бы 170 считывает значение разряда. Появление после этого состояния D

Подобный материал:

• Герберт Александер Саймон Исследователи ии: Лотфи Заде Исследователи ии: А. А ляпунов,, 9.34kb.
• «Как привлечь средства государственных институтов развития» Варшавский Владислав Римович, 48.54kb.
• Аннотация к научно-образовательному материалу, 114.81kb.
• 141. Поспелов В. И., Стальнов В. С. Содружественная аккомодация глаз при дисбинокулярной, 167.36kb.
• Тезисы докладов участников III международного конгресса «Россия и Польша: память империй, 1372.37kb.
• Д. А. Поспелов, Г. С. Осипов, 487.33kb.
• Варшавский А. С. Следы на дне, 1828.32kb.
• Рабочая программа учебной дисциплины Для направления 080100. 62 «Экономика» (программа, 562.39kb.
• Диспут с Пирром: прп. Максим Исповедник и христологические споры VII столетия / Отв, 73.89kb.
• Программа дисциплины: Имитационные модели для направления Прикладная математика и информатика, 120.53kb.

§ 5.3. Синхронизация и асинхронность

В рассмотренных выше задачах содержался не­который обман. Описанные модели решают задачу синхронизации, но используют при этом некий внут­ренний такт, который неизвестно откуда берется. И лишь в задаче о взаимной синхронизации через канал с неизвестной задержкой мы упомянули о воз­можности существования механизма, согласующего длительности внутренних тактов.

Задачу исключения понятия внутреннего такта нельзя решить в рамках используемой для описания алгоритмов локального поведения формальной мо­дели конечного автомата, так как она игнорирует реальное физическое время. Но как только мы на­чинаем рассматривать автомат как реальное физи­ческое устройство, он становится динамической системой, переходные процессы в которой не адек­ватны процессам смены состояний в модели конеч­ного автомата.

Преодоление указанных трудностей обеспечи­вается теорией согласованных самосинхронизующихся схем, которые обеспечивают инвариантность по­ведения автоматов по отношению к длительности внутреннего такта. Однако изложение идей и ре­зультатов этой теории выходит далеко за рамки настоящей книги. Мы опишем все же модель, в ко­торой синхронизация осуществляется без привлече­ния понятия жесткого такта.

На рис. 5.4 «стрелки» образовывали шеренгу, что соответствовало жесткой структурной организации.

160

Теперь мы рассмотрим возможность синхронизации «толпы». Пусть автоматы блуждают в некотором ограниченном пространстве и в какие-то моменты времени сталкиваются друг с другом. В отличие от моделей случайного парного взаимодействия, мы не предполагаем, что эти столкновения одновременны, и тем самым исключаем необходимость тактовой синхронизации. Для нашей модели, вернее для ее формального изучения, необходимо, чтобы в нашей толпе осуществлялось достаточно хорошее перемешивание, т. е. чтобы в идеале все столкновения были равновероятными. Перемешивание, порож­даемое процессами типа броуновского движения, несколько искажает получающиеся результаты. Столкнувшись, два автомата осуществляют акт взаимо­действия и расстаются. Возникает вопрос о существовании правил взаимодействия, обеспечивающих синхронизацию такой совокупности автоматов, пра­вил, не зависящих от числа автоматов.

Прежде всего уточним, что мы в этом случае понимаем под процессом синхронизации. В началь­ный момент времени все автоматы находятся в некотором состоянии 5о и при столкновении двух авто­матов, находящихся в этом состоянии, оно сохраняется у обоих автоматов. Внешний сигнал, иници­ирующий процесс синхронизации, поступает на один из автоматов и выводит его из начального состояния. Естественно, мы не можем требовать, чтобы через какое-то время все автоматы перешли в синхронное состояние, так как при случайном взаимодействии всегда существует ненулевая вероятность того, что информация об инициации процесса за любое конеч­ное время не выйдет за пределы ограниченной части автоматов. Поэтому при случайном взаимодействии можно говорить лишь о вероятности того, что значи­тельная доля автоматов одновременно или в течение относительно короткого отрезка времени будет на­ходиться в синхронном состоянии. Длительность этого отрезка времени определяется частотой столк­новений. Поскольку смена состояний автоматов есть результат взаимодействия, то по крайней мере все перешедшие в синхронное состояние автоматы долж­ны в течение этого интервала времени вступить во взаимодействие.

161


Качество, или точность, синхронизации мы будем оценивать математическим ожиданием доли автома­тов, находящихся в синхронном состоянии. Пусть у нас задано некоторое число  (0<<1) и мы мо­жем определить интервал времени t_, в течение кото­рого доля автоматов, превышающая 1—, заведомо вступит во взаимодействие. Мы будем говорить о синхронизации совокупности автоматов с точностью до е, если один из автоматов совокупности иницииро­ван в момент времени t₀ и существует такой момент времени t_c, что до этого момента математическое ожидание доли автоматов, перешедших в синхронное состояние, не превышает е, а математическое ожида­ние доли автоматов, перешедших в синхронное со­стояние после момента времени t_c+t_, превышает (1-).

Теперь можно рассмотреть алгоритм локального взаимодействия, обеспечивающий решение зада­чи синхронизации. Автомат имеет (k—1) внутрен­нее состояние. Состояние с номером 0 будем назы­вать начальным, а состояние с номером k — синх­ронным. Взаимодействие определяется следующими правилами:

1. Если оба взаимодействующих автомата нахо­дятся в состоянии 0, то они оба сохраняют это состояние.

2. Внешний инициирующий сигнал переводит автомат из состояния 0 в состояние 1.

3. Если по крайней мере один из взаимодейст­вующих автоматов имеет состояние, отличное от 0, то номер нового состояния для обоих автоматов равен увеличенному на единицу минимальному но­меру состояний взаимодействующих автоматов.

Попытаемся содержательно рассмотреть процесс синхронизации. Первый из инициированных извне автоматов переходит в состояние 1 и, сталкиваясь с автоматами, находящимися в состоянии 0, будет переводить их в состояние 1. Этот процесс обеспечит лавинообразное распространение переходов в со­стояние 1 в совокупности автоматов. Автомат в со­стоянии 1 сменит его на состояние 2, если он встре­тит автомат, находящийся также в состоянии 1, и вероятность этого события равна доле автоматов в состоянии 1. Если же автомат, в состоянии 2, встре­тится с автоматом в состоянии 0, то он возвратится

162

в состояние 1. Таким образом, если скорость пере­хода автоматов из состояния 0 в состояние 1 линей­но нарастает с ростом доли автоматов, находящихся в состоянии 1, то скорость перехода из состояния 1 в состояние 2, грубо говоря, возрастает, как корень квадратный от этой доли. И вообще, если в сово­купности имеется некоторое распределение автома­тов по номерам состояний, то доля автоматов с ма­лыми номерами состояний уменьшается с гораздо большей скоростью, чем увеличивается доля автома­тов с большими номерами состояний. Можно ожи­дать, что по мере продвижения этого распределения по номерам, его разброс будет возрастать. Иными словами, распределение автоматов по номерам будет «сгущаться» относительно номера текущего среднего состояния.

Это предположение подтверждается как матема­тическим анализом, так и результатами моделирова­ния поведения такой совокупности на ЭВМ. При моделировании в качестве одного такта выбиралось время, в течение которого все автоматы по одному разу вступают во взаимодействие. Тогда, например, в совокупности из 1024 автоматов при числе состоя­ний каждого автомата, равном 15, в 400 эксперимен­тах все автоматы переходили в синхронное состояние. Существенно здесь математическое доказательство независимости требуемого при данном е числа со­стояний автомата от общего числа автоматов в со­вокупности. Этот факт доказан для достаточно боль­ших размеров совокупности и достаточно малых . Однако это отнюдь не умаляет содержательного значения полученных результатов.

Результаты настоящего параграфа кажутся уди­вительными. Казалось бы, с ростом размера сово­купности задача согласования поведения должна усложняться, однако существуют весьма простые правила случайного взаимодействия, которые обес­печивают синхронизацию реакции совокупности на информацию, поступившую только одному индивиду­уму. Обеспечивающие этот эффект процессы, в ко­торых отстающие подтягиваются, а убежавшие впе­ред тормозятся, можно назвать процессами синхрофазировки. Возможно, что аналоги синхрофазировки встречаются и в эволюционных процессах. Случай­ные изменения, возникающие у отдельных индивиду-

163


умов вследствие случайных парных взаимодействий, распространяются по всей популяции и синхронно проявляются при возникновении соответствующих условий.

§ 5.4. Гимн однородным структурам

Читатели, наверное, заметили пристрастие авто­ров к однородным структурам с однотипно организо­ванным взаимодействием. Это действительно так. Нас не перестают удивлять и восхищать огромные возможности, скрытые в этих простейших, структу­рах. Только что одномерная однородная, структура продемонстрировала нам свою способность к синхро­низации без глобального синхронизующего, сигнала. Несколько ранее, в гл. 3 поливальные насосы вклю­чались на участках дач так, как нам этого хотелось. Здесь мы приведем еще несколько примеров из уди­вительного мира однородных структур. Отметим, что однородные структуры часто встречаются в биологии, а техника проявляет к ним особый интерес. Ведь однородные структуры легче производить, заменять и контролировать. Однородность и однотипность — идеал инженера. Вот почему в последние годы, осо­бенно после появления микроэлектроники, так возрос интерес к однородным структурам.

Мы думаем, что картина, описанная ниже, зна­кома всем читателям. В зале заседаний идет собра­ние. Председательствующий ставит на голосование какой-то проект или решение. «Прошу поднять руку тех, кто «за»,— говорит он. Поднимается лес рук. Подсчет числа голосов весьма трудоемок. Иногда председатель не справляется с ним и требуются специальные помощники — счетчики. «Кто «про­тив»? — снова спрашивает председатель. И опять лес рук. И снова надо считать. Хорошо, когда одно из мнений собирает мизерное число сторонников. Тогда и считать не требуется. Общая картина доста­точно красноречива. («Считать не будем? Я думаю, и так все ясно»,— говорит в этих случаях обычно председатель.) Но если «за» и «против» собрали примерно одинаковое число голосов, то публика на­чинает волноваться и требует перёголосования. Всег­да возникает мнение, что счетчики ошиблись. Как избежать этой щекотливой ситуации? Можно ли

164

автоматизировать подсчет голосов и определение ре­зультатов голосования? Удастся ли создать «машин­ку для голосования», которая давала бы нужный результат независимо от числа голосующих? Ответы на все эти вопросы положительны. Все это можно сделать с помощью одномерных и двумерных одно­родных структур. Проиллюстрируем наше утвержде­ние на наиболее простых примерах.

Рассмотрим сначала простейшее голосование, при котором каждый его участник голосует «за» или «против», а окончательное решение принимается по простому большинству голосов. Тогда, очевидно, каждую пару «за—против» можно вычеркнуть из дальнейшего сравнения. Если вычеркнуть все такие пары, то останутся только те, кто проголосовал «за» (если их большинство), или те, кто проголосовал «против». Считать их число не надо. Для простого большинства хватает и одного лишнего голоса. Эту процедуру вычеркивания конкурентных пар легко р
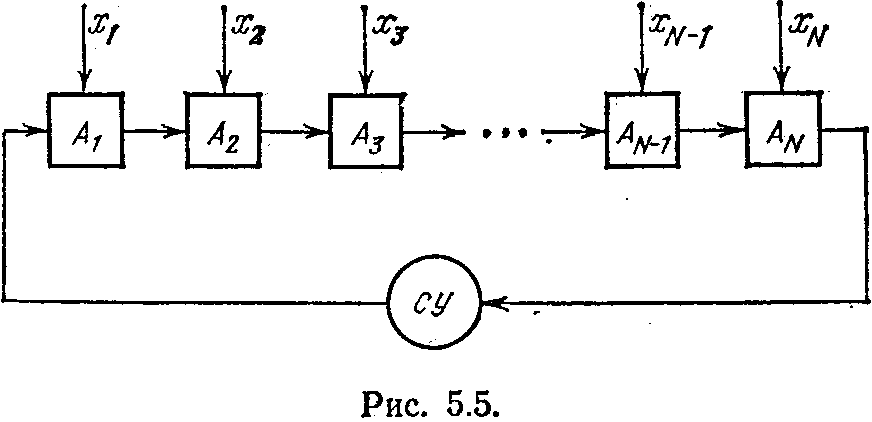
еализовать на одномерной однородной структуре. Рассмотрим схему, показанную на рис. 5.5. Каждый автомат имеет два состояния, которые мы обозначим через а, b. Состояние а соответствует тому, что дан­ный результат голосования еще не вычеркнут, со­стояние b — что он вычеркнут. На внешние входы автоматов поступают сигналы х_i от участников го­лосования. При этом х_i=1 означает, что i-й участник голосования проголосовал «против», a х_i=0 — что он проголосовал «за». Если голосование происходит в специально для этого оборудованном месте, то сигнал от каждого голосующего поступает в наше устройство в результате нажатия им соответствующей кнопки на индивидуальном пульте.

165


Сигналы, передаваемые по горизонтальной шине между автоматами, являются для системы внутрен­ними (рабочими). Работа автоматов в цепи задается табл. 5.1.

Таблица 5.1

	Входной с	игнал, поступив	вший от i-го гол	осующего
Рабочий сигнал	Хi Состояние	=0 aвтомата Ai	Хi состояние	=--1 aвтомата Ai
	A	b	А	b
So	S1, b	So, b	S2, b	So, b
S1	S1, а	S1, b	S3,b	S1, b
S2	S3, b	S2, b	S3, a	S2, b
S3	S3, a	S3,b	S3, a	S3, b

Поясним, как устроена эта таблица. В некотором такте работы на автомат Ai поступает входной сигнал Xi, равный 0 или 1, и один из четырех воз­можных рабочих сигналов. Сам Аi при этом нахо­дится в одном из двух возможных состояний (а или b). Значения входного и рабочего сигналов и состоя­ние автомата определяют текущую ситуацию, которая записывается парой символов: значением рабочего сигнала, выдаваемого автоматом Ai в этой текущей ситуации, и новое состоянием, в которое он пере­ходит.

В начале работы системное устройство СУ, по­казанное на рис. 5.5 в виде кружка, выдает на бо­ковой вход самого левого автомата цепи сигнал So. Все автоматы в начальном такте работы находятся в невычеркнутых состояниях а. Встретив первый автомат в состоянии а (в начальный такт работы это всегда будет крайний левый автомат в цепи), сигнал So переводит его в вычеркнутое состояние b. Если при этом на внешний вход автомата подавался сигнал «за», то далее по цепи будет вправо распро­страняться сигнал S1. Если же данный автомат имел на входе Xi=1 (т. е. сигнал «против»), то вправо бу­дет распространяться сигнал S2.

Сигналы S1 и S2 осуществляют поиск первого автомата, который мог бы составить вычеркиваемую

166

пару с отмеченным ими автоматом. Если при своем движении вправо сигналы S1 или S2 находят соот­ветствующий автомат, то он переводится в вычерк­нутое состояние, а рабочий сигнал становится рав­ным S3. Этот сигнал есть свидетельство вычеркива­ния одной пары из множества голосующих. Сигнал S3 «проскакивает» через все оставшиеся автоматы цепи, ничего не меняя на своем пути. Его приход в СУ свидетельствует об окончании одного акта вы­черкивания. Приход его в СУ заставляет системное устройство выдать на цепочку автоматов новый сиг­нал So. Окончание процесса вычеркивания произой­дет тогда, когда сигнал S1 или сигнал S2 не найдут себе подходящей пары для вычеркивания. В этом случае на вход СУ поступит не сигнал S3, a S1 или S2. Появление сигнала S1 говорит о том, что боль­шинство проголосовало «за», появление S2 — о про­тивоположном результате голосования. Особым слу­чаем является равенство голосов «за» и «против». В этой ситуации наше устройство посылает на боко­вой вход левого автомата цепи сигнал So, который «проскакивает» неизменным через все вычеркнутые автоматы и приходит на вход СУ. Это и есть сигнал

о равенстве голосов.

Отметим, что значение N нигде не фиксирова­лось и никакой роли для нас не играло. Устройство для подсчета голосов будет срабатывать верно при любом числе голосующих.

Мы рассмотрели простейший случай голосования. Но и для более сложных случаев задача об опреде­лении результатов голосования оказывается разре­шимой с помощью одномерной цепи автоматов, в которой сложность каждого автомата не зависит от того, сколько лиц приняло участие в процедуре голо­сования, а зависит лишь от вида голосования. Так, например, при голосовании по принципу 2/3 (реше­ние принимается, если за него проголосовало не менее 2/3 голосующих) сложность автоматов не меняется, а лишь увеличивается до шести число раз­личных рабочих сигналов. При одном «сканировании» с помощью сигнала So происходит вычеркивание тройки автоматов, на два из которых поступил сигнал «за», а на один — сигнал «против». Можно рассматривать задачу не с простым голосованием «за» и «против», а с выбором одного из К претендентов

167


по принципу большинства голосов. Это требует уже автоматов с четырьмя состояниями и восьми различ­ных рабочих сигналов. При последовательном голо­совании (например, сначала предлагается из трех претендентов B1, В2 и В3 выбрать либо B1, либо группу (В2, В3), и если выбран B1, то голосование заканчивается, а если группа, то на втором туре идет борьба между В2 и В3) требуется уже двумер­ная однородная структура. Такой же структуры требует и голосование, в котором каждый претендент на «призовое» место оценивается определенным коли-чеством очков.

Видов голосования человечество придумало очень много. Но интересно, что все они (по крайней мере, известные сегодня) можно промоделировать на одно­родных структурах, сложность элементов которых никак не зависит от числа голосующих.

Однородные структуры используются сейчас в самых разнообразных областях, хотя их применение и тормозится тем, что очень привычные вещи реали­зуются с их помощью весьма непривычным для чело­века образом. Возьмем, к примеру, операцию умно­жения. С детства мы привыкли умножать в столбик и верим, что этот способ самый простой и быстрый. На самом деле это совсем не так. Развитие вычи­слительной техники заставило нас перейти от деся­тичной системы к двоичной. В двоичной системе умножение оказалось куда более простым по своей структуре. Сдвиг на один разряд и сложение в опре­деленной последовательности дают тот же эффект умножения в столбик без необходимости помнить таблицу умножения. Вот как выглядит умножение 12 на 14 в двоичной системе:





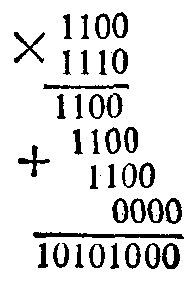
Здесь мы умножали, начиная со старшего разряда множителя, и производили сдвиги вправо. Конечно, можно было бы умножать, начиная с младшего раз­ряда множителя, и делать сдвиги влево. Результат

168

был бы одинаков. Как и при десятичном умножении, он равен 168.

Н
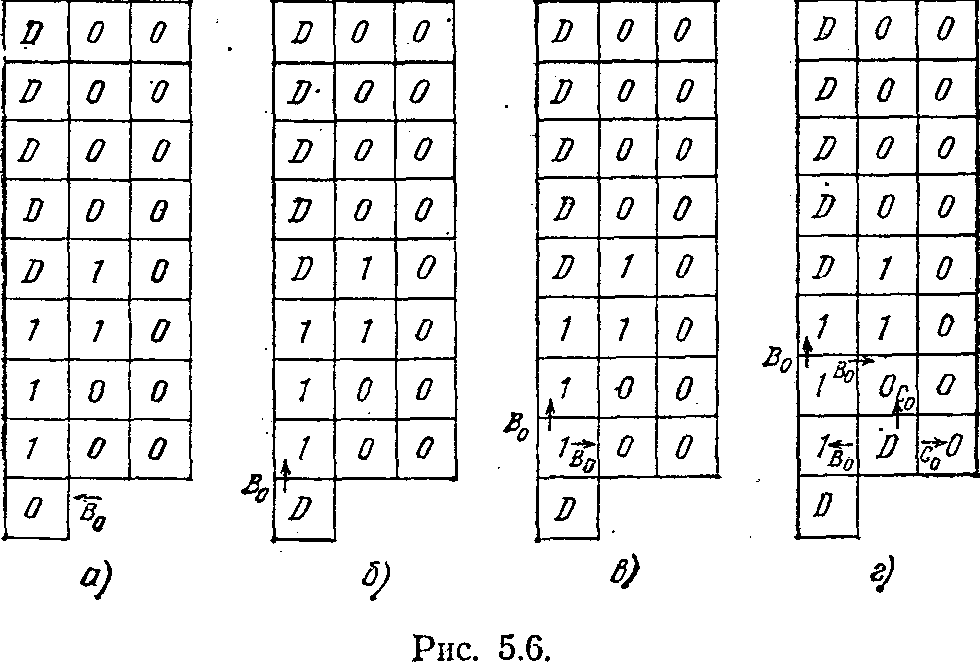
а рис. 5.6 показана однородная матрица, со­стоящая из трех столбцов, каждая клетка которых представляет собой однотипный автомат, имеющий три состояния D₀ , D₁ , D. Состояния D₀ и D₁ назы­ваются рабочими. Если автомат находится в них, то это означает, что он хранит в данной клетке значе­ние двоичной цифры 0 и 1 соответственно. Состоя­ние D является безразличным (нерабочим). Каждый


автомат имеет связи со всеми своими соседями. Эти входы и выходы мы будем обозначать буквами н, в, л, п (низ, верх, левый, правый). По ним могут передаваться сигналы пяти типов: безразличный (пустой) и B0, B1, Co, C1. Безразличный сигнал мы специально обозначать никак не будем. Сигналы Во и B1 несут информацию о значении цифр в со­ответствующем разряде множителя. Сигналы Со и С1, выдаваемые автоматами, соответствуют передаче соседу сигналов 0 и 1.

Число строк в матрице зависит от разрядности перемножаемых чисел. При n разрядах число строк в первом столбце равно 2n + 1, во втором и третьем столбцах —2n. Матрица, показанная на нашем ри­сунке, предназначена для перемножения четырех­разрядных двоичных чисел.

Все автоматы, образующие матрицу, функциони­руют одинаково. Этот принцип проистекает из одно-

169


родности среды. Работа автоматов иллюстрируется табл. 5.2.

Здесь индексы k, p, i могут принимать значения О или 1.

В этой таблице заполнены только те места, кото­рые соответствуют комбинациям сигналов и состоя­ний, встречающихся в процессе умножения. Звездочка означает, что этого сигнала может и не быть.

Как же происходит умножение? На рис. 5.6, а показано начальное заполнение матрицы. Множитель

Таблица 5.2

		Текущ	ий такт		По	следую	щий	такт
нет команды		вход		состо­яние		вход		состо­	Условие перехода
номер команды	п	л	н	авто­мата	п	в	л	яние
1			Ck	D				Dk
2			Ck	Dp		Ck		Dp
3	bo			Dp		Bp		D
4			Bk	Dp	Bk	Bk		Dp
5			Bk	D	Bk	Bk		D
6		B1		Dp	Cp	Cp	в»	D
7		Bо		Dp	Co	Cp	Во	D
8		Bl	Ck	Dp	Cp	Cp		Dk
9		Во	Ck	Dp	Co	Cp		Dk
10	Во			D				D
11		Ck	*Cp	Di		C1		D1	k + p + i = 3
		Ck	*Cp	Di		C1		D0	k + p + i = 2
		Ck	*Cp	Di		Co		D1	k + p + i = 1
		Ck	*Cp	Di		Co		Do	k + p + i = 0

записан в левом столбце так, что внизу находится младший разряд. Множимое написано в соседнем столбце. Правый столбец будет использоваться для получения произведения. Идея проста: если очеред­ная цифра множителя есть 0, то множимое надо сдви­нуть на один разряд вверх. Если же очередная цифра множителя есть 1, то до сдвига множителя его надо прибавить к той сумме, которая в этот момент будет накоплена в правом столбце матрицы.

Процесс начинается с подачи сигнала Во справа на младший разряд множителя. Этот сигнал как бы

170

считывает значение разряда. Появление после этого состояния D означает, что разряд считан (рис. 5.6, б). Далее сигнал Во распространяется вверх по левой колонке и на каждом уровне порождает сигнал Во направо. Эти сигналы сдвигают множимое без прибавления в накопленную сумму правой колон­ки матрицы. В нашем примере это происходит по­тому, что на начальном цикле разряд множителя был равен 0. На рис. 5.6, в, г показаны еще два такта работы однородной среды. Появление на рис. 5.6 г сигнала Во, приходящего в левую колонку, соответ­ствует началу работы с очередным разрядом множи­теля. Таким образом, на четвертом такте завершается микроцикл умножения.

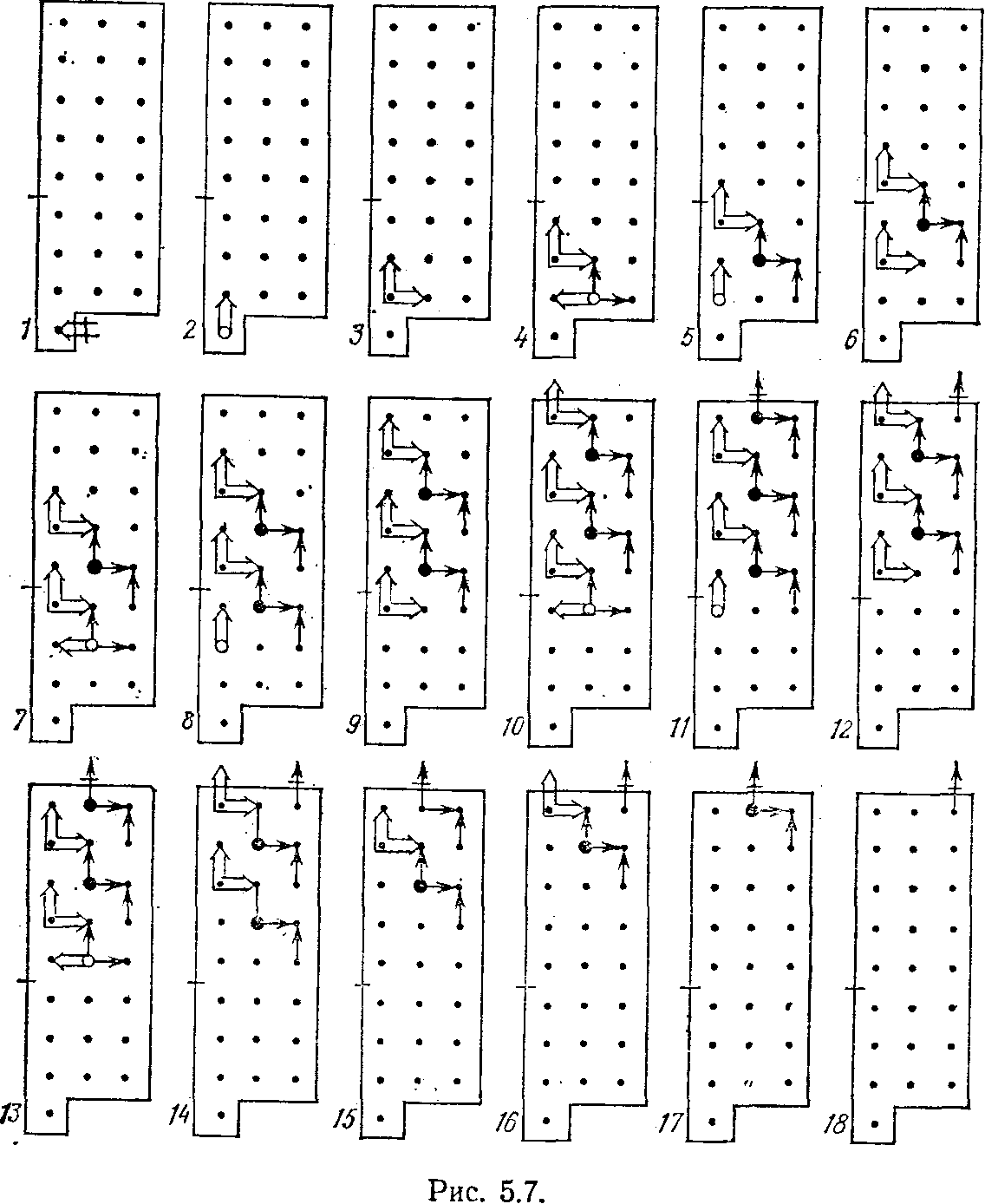
Общая картина распространения сигналов по однородной матрице при умножении двоичных чисел в столбик показана на рис. 5.7. На нем двойная стрелка изображает сигналы Bk, обычная стрелка — сигналы Ck. Светлый кружок означает переход автомата в данном такте в состояние D и выдачу вверх значения, соответствующего его состоянию, темный кружок — переход автомата в состояние Dp, соответствующего значению сигнала, поступив­шего на данный автомат снизу. Перечеркнутая стрел­ка означает, что передается либо сигнал Во, либо Со. За 18 тактов, как следует из рис. 5.7, цикл умноже­ния двух четырехразрядных двоичных чисел завер­шается. Состояния автоматов правой колонки хра­нят результат умножения. Сигналы, которые на рис. 5.7 как бы выходят за пределы матрицы, про­падают и не оказывают влияния на дальнейшее функционирование матрицы. Читатель, пользуясь табл. 5.2 и рис. 5.7, может самостоятельно завершить умножение 12 на 14 с помощью однородной мат­рицы.

Общее число тактов, которое нужно затратить на умножение двух n-разрядных двоичных чисел по предложенному методу, равно 8п+2. Если же отка­заться от привычной нам логики умножения и пе­рейти на более «изысканные» методы умножения, то однородная матрица позволяет найти произведение всего за 4n—1 такт работы. При этом сложность автоматов, образующих матрицу, даже меньше, чем при умножении в столбик. Правда, при умножении двух n-разрядных чисел потребуется в этом случае

171


n² + 1 автомат, а для рассмотренного нами случая — 6n + 1 автомат.

Кроме умножения, с помощью однородных мат­риц можно производить и деление. Один из способов





деления на однородной матрице с двумя столбцами требует автоматов той же сложности, что и для ум­ножения в столбик. Число необходимых автоматов равно 2п+3. Однородные среды открывают большие возможности в самых различных областях примене­ния. Например, они оказываются незаменимыми при обработке зрительной информации, отображаемой на

172

устройствах типа фотоматриц. Однородные автомат­ные структуры позволяют в этом случае выделять контуры отображаемых рисунков, находить вершины углов и точки пересечения, определять расстояние между изображениями на матрице и т. п. Развитие робототехники в последние годы стимулировало это направление исследований.

Для нас важно, что однородные структуры и од­нородные коллективы, состоящие из простых уст­ройств, способны решать многие задачи, для которых мы привыкли использовать традиционные последо­вательные (централизованные) способы решений. А трудность перехода к параллельным (децентрали­зованным) методам решения кроется, в частности, в нестандартности методов и алгоритмов, реализуемых в однородных структурах.

Наш гимн однородности не противоречит тому, что говорилось ранее о пользе неоднородности. В гл. 3 мы демонстрировали те новые качества, ко­торые неоднородность вносит в поведение коллекти­ва автоматов, решающих общую задачу. Ибо никто еще не доказал, что однородные коллективы и струк­туры могут эффективно решать все задачи, возника­ющие перед техническими системами. Но никто не доказал и противоположного!