Geum.ru

Учебно-методический комплекс дисциплины Бийск бпгу имени В. М. Шукшина

Вид материалаУчебно-методический комплекс

Содержание


Печатается по решениюредакционно-издательского советаБийского педагогического государственного университетаимени В.М. Шукшина
Д Дисциплина ДПП.Ф.08.
Рабочая программа
ДПП.Ф.08 Теория чисел
032100.00 (050201.65) «Математика» с дополнительной специальностью «Информатика»
Распределение по семестрам
ГОС направлений и специальностей высшего профессионального образования, утвержденного приказом Министерства образования и науки
Математики и методики обучения математике
Рабочая программа
2. Дидактические материалы (средства обучения)
3. Средства контроля
4. Методические рекомендации
1. Организационно-нормативная документация
Теория чисел
Содержание дисциплины
Модуль №2
Модуль №3.
Модуль №4.
1.1.4. учебно-методическая КАРТА дисциплины
1.1.5. Карта самостоятельной работы студента по дисциплине
...
Полное содержание
Подобный материал:
  1   2   3   4





Теория Чисел

Учебно-методический комплекс дисциплины


Бийск

БПГУ имени В.М. Шукшина

2008

Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

«Бийский педагогический государственный университет

имени В.М. Шукшина»


Теория Чисел


Учебно-методический комплекс дисциплины


Бийск

БПГУ имени В.М. Шукшина

2008


ББК Т

Печатается по решению
редакционно-издательского совета
Бийского педагогического государственного университета
имени В.М. Шукшина


Научный редактор:

канд. физ.-мат. наук, доцент А.М. Ерёмин


Рецензент:

канд. физ.-мат. наук, доцент Н.Н. Медведев


Д Дисциплина ДПП.Ф.08. Теория чисел: Учебно-методический комплекс дисциплины / Сост.: Л.М. Митрохина; Бийский пед. гос. ун-т им. В. М. Шукшина. – Бийск : БПГУ им. В. М. Шукшина, 2008 с….


Учебно-методический комплекс дисциплины разработан в соответствии с Государственным стандартом высшего профессионального образования. Он содержит учебную программу курса, материалы к лекционным и семинарским занятиям, методические рекомендации по организации самостоятельной работы студентов, контрольные задания для текущей и итоговой проверки знаний.

Для студентов педагогических вузов, обучающихся по специальности 032100.00 «математика – информатика».


 БПГУ им. В.М. Шукшина, 2008.

 Сост.: Л.М. Митрохина, 2008.

Утверждаю


Декан факультета

_______________

«_____» _______




Рабочая программа




Кафедра математики и методики обучения математике


(наименование кафедры, обеспечивающей преподавание дисциплины)


Шифр и наименование

дисциплины ДПП.Ф.08 Теория чисел

(шифр с указанием цикла подготовки (ГЭС, ЕН, ОПД, ДС, СД), наименование дисциплины)


Статус обязательная

(обязательная, элективная, факультативная)

Специальности 032100.00 (050201.65) «Математика» с дополнительной специальностью «Информатика»

(коды специальностей (направлений))


Формы обучения дневная

(дневная, заочная)


Объем дисциплины 90 часов

(общий объем дисциплины, час.)




Распределение по семестрам


Номер

семестра
Учебные занятия
Число

курсовых проектов (работ)

расчетных заданий
Форма итоговой аттестации (зачет, экзамен)

Общий объем
в том числе

аудиторные
Само-

стоят. работа

всего
из них

лекции
практич
кср.

4
90
46
18
28
4
40
1
зачет


Рабочая программа составлена на основании ГОС направлений и специальностей высшего профессионального образования, утвержденного приказом Министерства образования и науки РФ от 31.01.2005 года.


ДПП.Ф.08 Теория чисел


Делимость и простые числа. Основная теорема арифметики. Основное свойство простого числа. Неравенства Чебышева для (х). Теория сравнений. Кольцо и поле классов вычетов. Теоремы Эйлера и Ферма. Сравнения и системы сравнений с неизвестной величиной. Сравнения первой степени. Сравнения по простому модулю. Сравнения по степени простого числа. Редукция сравнения по составному модулю к сравнению по степени простого числа и к сравнению по простому модулю. Показатели чисел и классов по данному модулю. Число классов с заданным показателем. Теорема о существовании первообразного корня по простому модулю. Индексы чисел и классов по данному модулю. Двучленные сравнения по простому модулю. Квадратичные вычеты и невычеты. Символ Лежандра.

Арифметические приложения теории сравнений.

Цепные дроби. Существование и единственность значения цепной дроби. Представление действительных чисел цепными дробями. Теорема Лежандра о квадратичной иррациональности. Приближения действительных чисел подходящими дробями. Теорема Дирихле и ее применение к представлению простого числа р1(mod 4) в виде суммы двух квадратов.

Алгебраические и трансцендентные числа. Теорема Лиувилля и ее применение к построению трансцендентных чисел и к доказательству иррациональности.


Разработчик ст. преподаватель Л.М. Митрохина


Рабочая программа обсуждена на заседании кафедры


Математики и методики обучения математике


Заведующий кафедрой _____________________ Т.Д. Васильева.


Одобрена Ученым советом физико – математического факультета


«_______»_____________________ Председатель __________________________

Содержание

Рабочая программа



Пояснительная записка



1. Организационно-нормативная документация



1.1. Учебная программа



1.1.1. Цели и задачи дисциплины



1.1.2.Требования ГОС к содержанию курса



1.1.3. Содержание дисциплины



1.1.4. Учебно-методическая карта дисциплины



1.1.5. Карта самостоятельной работы студента по дисциплине



1.2. Карты ресурсов



1.2.1. Карта обеспечения дисциплины учебно-методической литературой

по дисциплине



1.2.2. Карта обеспечения дисциплины учебными материалами дисциплины



2. Дидактические материалы (средства обучения)



2.1. Печатные дидактические материалы



2.2. Электронные дидактические материалы



3. Средства контроля



3.1. Рейтинг-контроль

3.1. 1. Технологическая карта дисциплины

3.1.2. Рейтинговая книжка студента

3.2. Контрольно-измерительные материалы

3.2.1. Текущий контроль

3.2.2. Итоговый контроль




4. Методические рекомендации



4.1. Методические рекомендации для студентов

4.2. Методические рекомендации для преподавателей











Пояснительная записка

1. ОРГАНИЗАЦИОННО-НОРМАТИВНАЯ ДОКУМЕНТАЦИЯ

1.1. Учебная программа

1.1.1. Цели и задачи дисциплины

Теория чисел является наукой о числовых системах с их связями и законами. При этом наиболее подробно рассматривается арифметика целых чисел, поскольку этот раздел является базисом для дальнейшего построения самой теории чисел.

Теория чисел изучает числа с точки зрения их строения и внутренних связей, рассматривает возможности представления одних чисел через другие, более простые по своим свойствам.

Предмет знакомит с основными проблемами теории чисел и различными методами исследования ее задач. Предпочтение отдается элементарным методам, которые в основном используют сведения из элементарной математики. Это методы теории сравнений, методы непрерывных дробей и другие. В качестве арифметических приложений теории сравнений рассматриваются применения сравнений к выводу признаков делимости, к проверке результатов арифметических действий, к нахождению остатков от деления, к нахождению длины периода систематической дроби при помощи свойств показателя. Рассматриваются неопределенные уравнения. Дисциплина дает общее представление о приближении действительных чисел рациональными дробями.

Содержание дисциплины «Теория чисел» богата вопросами, интересными учителю, имеет непосредственное отношение к математике средней школы. Достаточное время отводится на решение задач, связанных со школьным курсом.

Прослушав курс «Теория чисел», студент должен уметь:
  • выполнять деление одного целого числа на другое с остатком, знать свойства делимости, иметь четкое представление о простых и составных числах, уметь разлагать составное число на простые множители, находить наибольший общий делитель и наименьшее общее кратное целых чисел, как по их каноническому разложению, так и с помощью алгоритма Евклида;
  • уметь доказывать основные теоремы теории чисел и применять их к решению задач (нахождение остатка от деления с помощью теорем Эйлера и Ферма и др.);
  • знать определение сравнимых по модулю чисел, основные свойства сравнений и уметь применять их к решению сравнений с одним неизвестным и решению неопределенных уравнений вида ах+by=c;
  • уметь решать системы сравнений первой степени;
  • уметь определять порядок числа (класса вычетов) по данному модулю, знать, что такое индекс числа (класса вычетов) по простому модулю, знать свойства индексов и уметь ими пользоваться при решении двучленных сравнений по простому модулю, уметь находить символ Лежандра;
  • знать, как представить рациональное число конечной цепной дробью, уметь применять свойства подходящих дробей к решению конкретных задач, уметь решать сравнения и неопределенные уравнения вида ах+by+с=0 с помощью подходящих дробей;
  • знать о представлении чисел цепными дробями, уметь определять погрешность замены;
  • иметь представление об алгебраических и трансцендентных числах;
  • знать признаки делимости, уметь определять длину периода и вид десятичной дроби, в которую обращается заданное рациональное число.



1.1.2. Требования ГОС к содержанию курса

ДПП.Ф.08 Теория чисел

Делимость и простые числа. Основная теорема арифметики. Основное свойство простого числа. Неравенства Чебышева для (х). Теория сравнений. Кольцо и поле классов вычетов. Теоремы Эйлера и Ферма. Сравнения и системы сравнений с неизвестной величиной. Сравнения первой степени. Сравнения по простому модулю. Сравнения по степени простого числа. Редукция сравнения по составному модулю к сравнению по степени простого числа и к сравнению по простому модулю. Показатели чисел и классов по данному модулю. Число классов с заданным показателем. Теорема о существовании первообразного корня по простому модулю. Индексы чисел и классов по данному модулю. Двучленные сравнения по простому модулю. Квадратичные вычеты и невычеты. Символ Лежандра.

Арифметические приложения теории сравнений.

Цепные дроби. Существование и единственность значения цепной дроби. Представление действительных чисел цепными дробями. Теорема Лежандра о квадратичной иррациональности. Приближения действительных чисел подходящими дробями. Теорема Дирихле и ее применение к представлению простого числа р1(mod 4) в виде суммы двух квадратов.

Алгебраические и трансцендентные числа. Теорема Лиувилля и ее применение к построению трансцендентных чисел и к доказательству иррациональности.


1.1.3. Содержание дисциплины

ДПП.Ф.08 Теория чисел

Модуль №1. Основные понятия и теоремы.


Раздел I.

Тема 1. Делимость целых чисел. Теорема о делении с остатком. Наибольший общий делитель. Наименьшее общее кратное. Простые и составные числа. Свойства простых чисел. Признак простоты числа. Основная теорема арифметики. Бесконечность множества простых чисел. Неравенство Чебышева для .


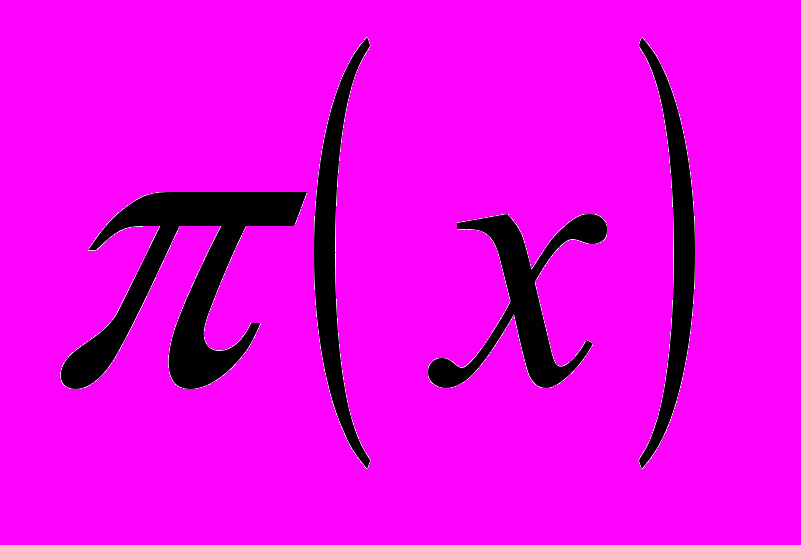МОДУЛЬ №2.Цепные дроби.


Раздел I.

Тема 1. Конечные цепные дроби. Разложение рационального числа в конечную цепную дробь. Подходящие дроби. Свойства подходящих дробей.


МОДУЛЬ №3.Сравнения в кольце целых чисел.


Раздел I.

Тема 1. Сравнения по модулю, их основные свойства. Кольцо классов вычетов. Полная и приведенная системы вычетов. Мультипликативная группа обратимых элементов в кольце классов вычетов. Поле классов вычетов по простому модулю. Функция Эйлера. Теоремы Эйлера и Ферма.

Тема 2. Сравнения с неизвестной величиной. Сравнения первой степени. Критерий разрешимости и число решений. Решение сравнений первой степени методом подбора, методом преобразования коэффициентов, по формуле Эйлера, с помощью подходящих дробей.

Тема 3. Сравнения по простому модулю. Сведение к наиболее простому виду. Максимальное число решений. Теорема Вильсона. Сравнения по степени простого числа. Редукция сравнения по составному модулю к сравнению по степени простого числа и к сравнениям по простому модулю.


Раздел II.

Тема 1. Показатели чисел и классов по данному простому модулю. Число классов с заданным показателем. Теорема о существовании первообразного корня по простому модулю. Индексы чисел и классов по данному модулю. Основные свойства индексов. Таблицы индексов. Применение индексов к решению двучленных сравнений по простому модулю. Квадратичные вычеты и невычеты. Символ Лежандра.


Раздел III.

Тема 1. Арифметические приложения теории сравнений. Вычисление остатков при делении на данное число. Признаки делимости. Определение длины периода, получающегося при обращении обыкновенной дроби в десятичную.


МОДУЛЬ №4. Бесконечные цепные дроби.

Раздел I.

Тема 1. Бесконечные цепные дроби. Сходимость бесконечных цепных дробей. Разложение действительных чисел в цепные дроби. Квадратичные иррациональности и периодические цепные дроби. Теорема Лагранжа о квадратичной иррациональности.

Тема 2. Приближение действительных чисел подходящими дробями. Теорема Дирихле, ее применение к представлению простого числа 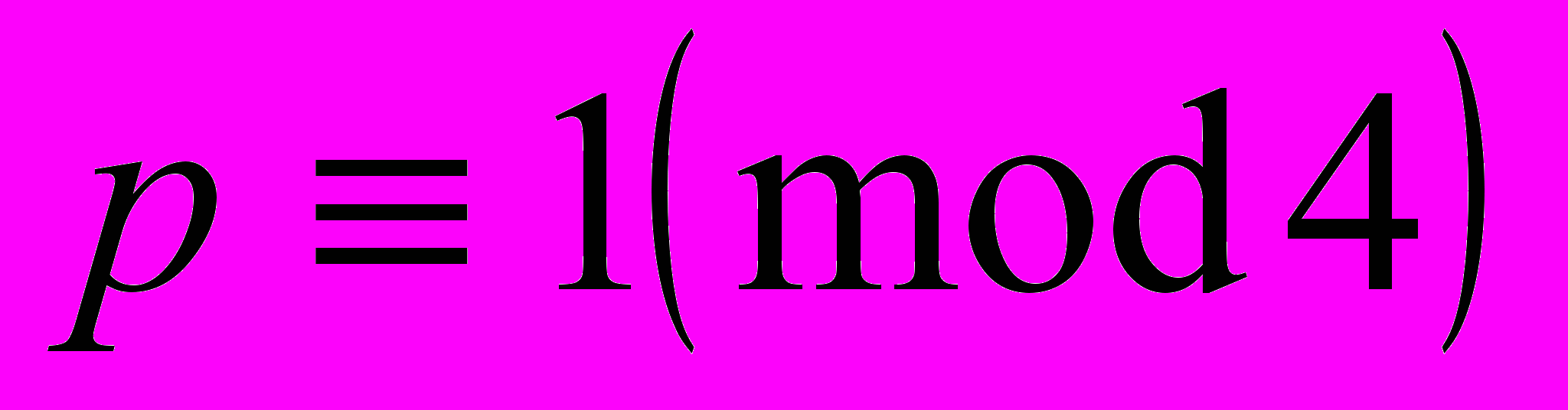в виде суммы двух квадратов. Алгебраические и трансцендентные числа. Теорема Лиувилля и ее применение к построению трансцендентных чисел и к доказательству иррациональности.


Таблица 1

1.1.4. учебно-методическая КАРТА дисциплины


__Ф__│__Р__│_­­­­_В____ ДПП.Ф.08.Теория чисел 90

(наименование) кол-во часов (общее)


для студентов образовательной профессиональной программы

специальность 032100.00 (050201.65) «Математика» с дополнительной специальностью «Информатика»

по дневной форме обучения


Модуль
Трудоемкость
№№ раздела,

темы
Лекционный курс
Занятия (номера)
Индивидуальные занятия

Самостоятельная работа студентов
Формы контроля

В кредитах
В часах
Вопросы, изучаемые на лекции
Часы
семинарские
Лабораторно-практические
Содержание

Часы
Содержание (или номера заданий)
Часы

№1



6
Раздел I,

Тема 1
Делимость целых чисел. Теорема о делении с остатком. Наибольший общий делитель. Наименьшее общее кратное. Простые и составные числа. Признак простоты числа. Основная теорема арифметики. Бесконечность множества простых чисел. Неравенство Чебышева для π(х).
2



Занятие 1.


Занятие 2.
.





(5) 1, 30, 31.

(6) 1-51.

Изучение теоретичес-кого материала, выполнение ИЗ.


(5) 22-29, 36-38.

Изучение теоретичес-кого материала, выполнение ИЗ.


3


3


Проверка на занятии.


Проверка на занятии. Самостоятельная работа.

№2



4
Раздел I,

Тема 1
Конечные цепные дроби. Разложение рационального числа в конечную цепную дробь. Подходящие дроби. Свойства подходящих дробей.
2



Занятие 3.






(6) 75-98, 125-162

(5) 249-254.

Работа с определениями и доказательствами теорем. Выполнение ИЗ.
3
Контрольный опрос.

№3



6
Раздел I,

Тема 1
Сравнения по модулю, их основные свойства. Кольцо классов вычетов. Полная и приведенная системы вычетов. Мультипликативная группа обратимых элементов в кольце классов вычетов. Поле классов вычетов по простому модулю. Функция Эйлера. Теоремы Эйлера и Ферма.
2



Занятие 4.


Занятие 5.






(6) 75-98, 125-162

(5) 249-254.

Выполнение ИЗ. Изучение теоретического материала.


(5) 97-101, 109-110, 152-159

(6) 367-388.
3


3
Проверка задания на занятии.


Самостоятельная работа.




6
Раздел I,

Тема 2
Сравнения с неизвестной величиной. Сравнения первой степени. Критерий разрешимости и число реше-ний. Решение методом подбора, методом преобразова-ния коэффи-циентов, по формуле Эйлера, с по-мощью подходящих дробей.
2



Занятие 6.


Занятие 7.








(5)174-176.

Подготовка к колок-виуму.


(5)179-181, 194-198.

(6)163-208, 253-304.

Подготовка к коллоквиуму.
3


3


Проверка задания на занятии.

Теоретичес-кий опрос.


Проверка задания на занятии.




6
Раздел I,

Тема 3
Сравнения по простому мо-дулю. Сведе-ние к наиболее простому виду. Макси-мальное число решений. Сравнения по степени простого числа. Редук-ция сравнения по составному модулю к сравнению по степени простого числа и к сравне-ниям по прос-тому модулю.
2



Занятие 8.
Коллоквиум
2


(5)184-186, 199-202, 209-211.

(6)305-330
4


Теоретичес-кий опрос.

Проверка заданий на занятии.




4
Раздел II,

Тема 1
Показатели чисел и классов по данному модулю. Число классов с заданным показателем. Теорема о су-ществовании первообразно-го корня по простому модулю. Индексы чисел и классов по простому модулю. Основные свойства индексов. Таблицы индексов. Применение индексов к ре-шению дву-членных срав-нений по простому мо-дулю. Квадра-тичные выче-ты и невычеты Символ Лежандра.






Занятие 9.








(5) 246

(6) 389-391

Изучение теоретического материала.
3


Проверка заданий на занятии.







4
Раздел III,

Тема 1
Арифметические приложения теории сравнений. Вычисление остатков при делении на данное число. Признаки делимости. Определение длины периода, получающегося при обра-щении обыкновенной дроби в десятичную.
2



Занятие 10.








(5) 229-232

Подготовка теоретического материала. Выполнение ИЗ.

3


Проверка заданий на занятии.

Самостоятельная работа



№4



8
Раздел I,

Тема 1
Бесконечные цепные дроби. Сходимость бесконечных цепных дро-бей. Разложе-ние действии-тельных чисел в цепные дроби. Квад-ратичные иррациональности и пери-одические цепные дроби. Теорема Лагранжа о квадратичной иррациональности.
2



Занятие 11.


Занятие 12.


Защита ИЗ.


2


(5) 234-242.

Выполнение ИЗ. Изучение теоретического материала.


(5) 212-217, 243.

Подготовка к контрольной работе.
3


4


Проверка заданий на занятии.


Контрольный опрос.




6
Раздел I,

Тема 2
Приближение действительных чисел подхо-дящими дро-бями. Теорема Дирихле, ее применение к представле-нию простого числа 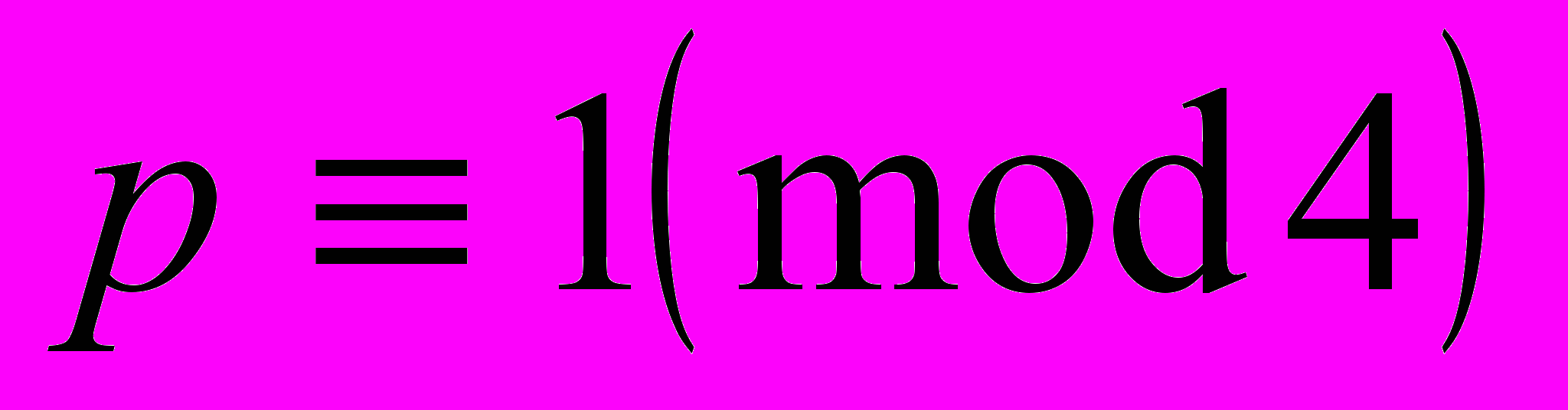в виде суммы двух квадратов

Алгебраичес-кие и транс-цендентные числа. Теорема Лиувилля и ее применение к построению трансцендент-

ных чисел и к доказательству иррациональности.
2



Занятие 13.


Занятие 14.








(5) 255-260, 264-266

(6) 99
3


3


Контрольная работа.


Таблица 2

1.1.5. КАРТА САМОСТОЯТЕЛЬНОЙ РАБОТЫ СТУДЕНТА ПО ДИСЦИПЛИНЕ


__Ф__│__Р__│_­­­­_В____ ДПП.Ф.08.Теория чисел 90

(наименование) кол-во часов (общее)


для студентов образовательной профессиональной программы

специальность 032100.00 (050201.65) «Математика» с дополнительной специальностью «Информатика»

по дневной форме обучения


Модуль
Номер раздела, темы
Самостоятельная работа студентов
Формы контроля

Содержание работы, формы работы
Сроки выполнения
Общая трудоемкость

№1
I; 1
(5) 1, 30, 31.

(6) 1-51.

Изучение теоретического материала, выполнение ИЗ.



3
Проверка задания на занятии.

№1
I; 2
(5) 22-29, 36-38.

Изучение теоретического материала, выполнение ИЗ.



3
Проверка на занятии. Самостоятельная работа.

№2
I; 1
(6) 75-98, 125-162

(5) 249-254.

Работа с определениями и доказательствами теорем. Выполнение ИЗ.



3
Контрольный опрос.

№3
I; 1
(6) 75-98, 125-162

(5) 249-254.

Выполнение ИЗ. Изучение теоретического материала.



3
Проверка задания на занятии.

№3
I; 1
(5) 97-101, 109-110, 152-159

(6) 367-388.



3
Самостоятельная работа.

№3
I; 2
(5)174-176.

Подготовка к колоквиуму.



3
Проверка задания на занятии.

№3
I; 2
(5)179-181, 194-198.

(6)163-208, 253-304.

Подготовка к коллоквиуму.



3
Проверка задания на занятии.

№3
I; 3
(5)184-186, 199-202, 209-211.

(6)305-330



4
Коллоквиум.

№3
II; 1
(5) 246

(6) 389-391

Изучение теоретического материала.



3
Проверка заданий на занятии.

№3
III; 1
(5) 229-232

Подготовка теоретического материала. Выполнение ИЗ.



3
Проверка заданий на занятии.

Самостоятельная работа

№4
I; 1

(5) 234-242.

Выполнение ИЗ. Изучение теоретического материала.



3
Проверка заданий на занятии.

№4
I; 1
(5) 212-217, 243.

Подготовка к контрольной работе



4
Проверка заданий на занятии.

№4
I; 2






3
Проверка заданий на занятии.

№4
I;2
(5) 255-260, 264-266

(6) 99



3




Таблица 3

1.2. КАРТЫ РЕСУРСОВ

1.2.1. Карта обеспечения дисциплины учебно-методической литературой по дисциплине

__Ф__│__Р__│_ В Теория чисел (90 часов)\


для студентов образовательной профессиональной программы

специальность 032100.00 (050201.65) «Математика» с дополнительной специальностью «Информатика»

по дневной форме обучения


№

п/п
Наименование
Наличие

место/ (кол-во экз.)
Потребность
Примечания




Основная литратура.












Модуль №1









1.
Сизый С.В. Лекции по теории чисел.-М.: Физматлит, 2007.
20
35
Библиотека БПГУ

2.
Грибанов В.У., Титов П.И.. Сборник упражнений по теории чисел.-М.: Просвещение, 1964.
65
35
Библиотека БПГУ

3.
Смолин Ю.Н. Алгебра и теория чисел.-М.: Флинта, 2006.
20
35
Библиотека БПГУ

4.
Шнеперман Л.Б.Сборник задач по алгебре и теории чисел. Учебное пособие.3-еизд., стер.-СПб.:Лань, 2008.-224 с.
20
20
Библиотека БПГУ




Модуль №2









5.
Грибанов В.У., Титов П.И.. Сборник упражнений по теории чисел.-М.: Просвещение, 1964.
65
35
Библиотека БПГУ

6.
Сизый С.В. Лекции по теории чисел.-М.: Физматлит, 2007.
20
35
Библиотека БПГУ

7.
Смолин Ю.Н. Алгебра и теория чисел.-М.: Флинта, 2006.
20
35
Библиотека БПГУ

8.
Шнеперман Л.Б.Сборник задач по алгебре и теории чисел. Учебное пособие.3-еизд., стер.СПб.:Лань,2008.-224 с.
20
20
Библиотека БПГУ




Модуль №3









9.
Грибанов В.У., Титов П.И.. Сборник упражнений по теории чисел.-М.: Просвещение, 1964.
65
35
Библиотека БПГУ

10.
Сизый С.В. Лекции по теории чисел.-М.: Физматлит, 2007.
20
35
Библиотека БПГУ

11.
Смолин Ю.Н. Алгебра и теория чисел.-М.: Флинта, 2006.
20
35
Библиотека БПГУ

12.
Шнеперман Л.Б.Сборник задач по алгебре и теории чисел. Учебное пособие.3-еизд., стер.-СПб.:Лань, 2008.-224 с.
20
20
Библиотека БПГУ

13.
Грибанов В.У., Титов П.И.. Сборник упражнений по теории чисел.-М.: Просвещение, 1964.
65
35
Библиотека БПГУ




Модуль №4









14.
Грибанов В.У., Титов П.И.. Сборник упражнений по теории чисел.-М.: Просвещение, 1964.
65
35
Библиотека БПГУ

15.
Сизый С.В. Лекции по теории чисел.-М.: Физматлит, 2007.
20
35
Библиотека БПГУ




Дополнительная литература












Модуль №1









16.
Кочева А.А. Задачник-практикум по алгебре и теории чисел. Часть III.- М.:Просвещение,
5
5
Кабинет математики

17.
Виноградов И.М. Основы теории чисел.-М.: Наука, 1972.
64



Библиотека БПГУ

18.
Бухштаб А.А. Теория чисел.-М.: Просвещение, 1966.
35
35
Библиотека БПГУ




Модуль №2









19.
А.А. Кочева Задачник-практикум по алгебре и теории чисел. Часть III.- М.:Просвещение, 1984.
5
5
Кабинет математики

20.
Виноградов И.М. Основы теории чисел.-М.: Наука, 1972.
64
35
Библиотека БПГУ

21.
Бухштаб А.А. Теория чисел.-М.: Просвещение, 1966.
35
35
Библиотека БПГУ




Модуль №3









22.
Кочева А.А. Задачник-практикум по алгебре и теории чисел.. Часть III.- М.:Просвещение, 1984.
5
5
Кабинет математики

23.
Виноградов И.М. Основы теории чисел.-М.: Наука, 1972.
64
35
Библиотека БПГУ

24.
Бухштаб А.А. Теория чисел.-М.: Просвещение, 1966.
35
35
Библиотека БПГУ




Модуль №4.









25.
Михелович Ш.Х. Теория чисел.-М.:Высшая школа, 1962.
2
2
Библиотека БПГУ

26.

Феферман С.Ф. Числовые системы.-М.; Просвещение, 1971.



35



27.
Виноградов И.М. Основы теории чисел.-М.: Наука, 1972.
64
35
Библиотека БПГУ


Таблица 4

1.2.2. Карта обеспечения дисциплины учебными материалами дисциплины

__Ф__│__Р__│_ В Теория чисел (90 часов)\


для студентов образовательной профессиональной программы

специальность 032100.00 (050201.65) «Математика» с дополнительной специальностью «Информатика»

по дневной форме обучения


№

п/п
Наименование
Вид
Форма доступа
Рекомендуемое

использование
Потребность

1
Борзенко Е.К. Функции комплексного переменного. – Бийск: БПГУ им. В. М. Шукшина,2008. – 54 с.
Печатный,

электронный
Библиотека БПГУ,(50экз.).


(Внутренний сайт ФМФ)
Очная форма - печатное

Заочная форма – печатное

40 экземпляров

2
Конспекты лекций/ Борзенко Е.К.

Электронный (Word).
Кабинет методики математики, ФМФ
Очная, заочная формы – электронное



3
Математика. Избранные вопросы ТФКП.

ссылка скрыта moodle 2008.
(Word).

Сетевой
Портал УИНФ БПГУ
Электронное

Сетевое




2. Дидактические материалы (средства обучения)

2.1. Печатные дидактические материалы

Обязательная литература

  1. Виноградов И.М. Основы теории чисел. – М.: Наука, 1972.
  2. Бухштаб А.А. Теория чисел. – М.: Просвещение, 196
  3. Сизый С.В. Лекции по теории чисел. - М.: Флинта, 2006.
  4. Смолин Ю.Н. Алгебра и теория чисел. - М.: Флинта, 2006.
  5. Грибанов В.У., Титов П.И. Сборник упражнений по теории чисел. – М.: Просвещение, 1964.


Дополнительная литература
  1. Кочева А.А. Задачник-практикум по алгебре и теории чисел. Часть III. – М., Просвещение, 1984.
  2. Михелович Ш.Х. Теория чисел. – М.: Высшая школа, 1962.
  3. Куликов Л.Я. Алгебра и теория чисел. – М.: Высшая школа, 1979.
  4. Феферман С.Ф. Числовые системы. – М.: Наука, 1971.
  5. Нечаев В.А. Числовые системы. – М., Просвещение, 1975.


2.2. Электронные дидактические материалы

1. Борзенко Е.К. Математика. Избранные вопросы ТФКП. ссылка скрыта.

2. Борзенко Е.К. Функции комплексного переменного. www.fmf.bigpi.biysk.ru

3. СРЕДСТВА КОНТРОЛЯ

3.1. РЕЙТИНГ-КОНТРОЛЬ

3.1. 1. Технологическая карта дисциплины

Наименование

дисциплины/курса
Уровень/ступень образования

(бакалавриат, магистратура)
Статус дисциплины

в рабочем учебном плане

(А, В, С)
Количество зачетных единиц/кредитов

Теория чисел

Специалист



кредита (ЗЕТ)

Смежные дисциплины по учебному плану

Предшествующие: математический анализ, алгебра, геометрия




Последующие: курсы по выбору, числовые системы




Входной МОДУЛЬ

(проверка «остаточных» знаний по ранее изученным смежным дисциплинам)

Форма работы*
Количество баллов 3 %

min
max

Тест 1
0
3

Итого
0
3




БАЗОВЫЙ МОДУЛЬ № 1. Основные понятия и теоремы.




Форма работы*
Количество баллов 11 %

min
max

Текущая работа:









Лекция
посещение
0
1

Практические занятия
посещение
0
3




работа у доски
0
3

Промежуточный контроль
самостоятельная работа
0
4

Итого
0
11

БАЗОВЫЙ МОДУЛЬ № 2. Цепные дроби.




Форма работы*
Количество баллов 17 %

min
max

Текущая работа:









Лекция
посещение
0
1

Практическое занятие
посещение
0
1




работа у доски
0
1

Промежуточный контроль
Самостоятельная работа

коллоквиум
0
4

10

Итого



0
17

БАЗОВЫЙ МОДУЛЬ № 3. Сравнения в кольце целых чисел.




Форма работы
Количество баллов 35%

Текущая работа:









Лекции
посещение
0
5

Практические занятия
посещение
0
8




работа у доски
0
8

Промежуточный контроль
самостоятельная работа

коллоквиум
0
4

10

Итого



0
35

БАЗОВЫЙ МОДУЛЬ № 4. Бесконечные цепные дроби.




Форма работы
Количество баллов 10 %

Текущая работа:









Лекции
посещение
0
2

Практические занятия
посещение
0
2




работа у доски
0
2

Промежуточный контроль
Самостоятельная работа
0
4




1






Итого



0
10

Всего зо 4 модуля



0
76




Итоговый модуль

тестирование** (итоговое)






Контрольная работа
0
9

Индивидуальное задание
0
15

Итого



24




Общее количество баллов по дисциплине

(по итогам изучения всех модулей, без учета дополнительного модуля)
min
Max

60
100

*Перечень форм работы текущей аттестации определяется кафедрой или ведущим преподавателем

** Дополнительная возможность повысить рейтинг.


ФИОпреподавателя:__МитрохинаЛ.М..______________________________________

Утверждено на заседании кафедры «___»_______200__г. Протокол №______

Зав.кафедрой________________________

3.1.2. Рейтинговая книжка студента

по дисциплине «Теория чисел»


Максимальное количество баллов – 100%

Минимальное количество баллов – 60 %


Формы рейтингового оценивания:

I.

Вид теста
КОЛ-ВО БАЛЛОВ

Тест 1. Разложение на простые множители, НОД, НОК, признаки делимости.

(Тест на проверку «остаточных» знаний по школьной математике)