Учебно-методический комплекс дисциплины Бийск бпгу имени В. М. Шукшина
| Вид материала | Учебно-методический комплекс |
- Учебно-методический комплекс дисциплины Бийск бпгу имени В. М. Шукшина, 2836.1kb.
- Учебно-методический комплекс дисциплины Бийск бпгу имени В. М. Шукшина, 2979.19kb.
- Учебно-методический комплекс дисциплины Бийск бпгу имени В. М. Шукшина, 2143.51kb.
- Учебно-методический комплекс дисциплины Бийск бпгу имени В. М. Шукшина, 785.31kb.
- Учебно-методический комплекс дисциплины Бийск бпгу имени В. М. Шукшина, 793.69kb.
- Учебно-методический комплекс дисциплины Бийск бпгу имени В. М. Шукшина, 901.29kb.
- Учебно-методический комплекс дисциплины Бийск бпгу имени В. М. Шукшина, 2591.69kb.
- Учебно-методический комплекс дисциплины Бийск бпгу имени В. М. Шукшина, 814.76kb.
- Учебно-методический комплекс дисциплины Бийск бпгу имени В. М. Шукшина, 2075.7kb.
- Учебно-методический комплекс дисциплины Бийск бпгу имени В. М. Шукшина, 1147.22kb.
Максимальное количество баллов – 3% (3 балла)
Минимальное количество баллов – 0 %
II.
| ТЕМА ЛЕКЦИИ | КОЛ-ВО ЧАСОВ | ПОСЕЩ-ТЬ | КОЛ-ВО БАЛЛОВ |
| Лекция № 1 Делимость целых чисел. Теорема о делении с остатком. Наибольший общий делитель. Наименьшее общее кратное. Простые и составные числа. Свойства простых чисел. Признак простоты числа. Основная теорема арифметики.
| 2 | | |
| Лекция № 2 Конечные цепные дроби. Разложение рационального числа в конечную цепную дробь. Подходящие дроби. Свойства подходящих дробей | 2 | | |
| Лекция № 3. Сравнения по модулю, их основные свойства. Кольцо классов вычетов. Полная и приведенная системы вычетов. Мультипликативная группа обратимых элементов в кольце классов вычетов. Поле классов вычетов по простому модулю. Функция Эйлера. Теоремы Эйлера и Ферма | 2 | | |
| Лекция № 4. Сравнения с неизвестной величиной. Сравнения первой степени. Критерий разрешимости и число решений. Решение методом подбора, методом преобразования коэффициентов, по формуле Эйлера, с помощью подходящих дробей. | 2 | | |
| Лекция № 5Сравнения по простому модулю. Сведение к наиболее простому виду. Максимальное число решений. Теорема Вильсона. Сравнения по степени простого числа. Редукция сравнения по составному модулю к сравнению по степени простого числа и к сравнениям по простому модулю | 2 | | |
| Лекция № 6Показатели чисел и классов по данному простому модулю. Число классов с заданным показателем. Теорема о существовании первообразного корня по простому модулю. Индексы чисел и классов по данному модулю. Основные свойства индексов. Таблицы индексов. Применение индексов к решению двучленных сравнений по простому модулю. Квадратичные вычеты и невычеты. Символ Лежандра | 2 | | |
| Лекция № 7. Арифметические приложения теории сравнений. Вычисление остатков при делении на данное число. Признаки делимости. Определение длины периода, получающегося при обращении обыкновенной дроби в десятичную. | 2 | | |
| Лекция № 8Бесконечные цепные дроби. Сходимость бесконечных цепных дробей. Разложение действительных чисел в цепные дроби. Квадратичные иррациональности и периодические цепные дроби. Теорема Лагранжа о квадратичной иррациональности | 2 | | |
| Лекция № 9Приближение действительных чисел подходящими дробями. Теорема Дирихле, ее применение к представлению простого числа 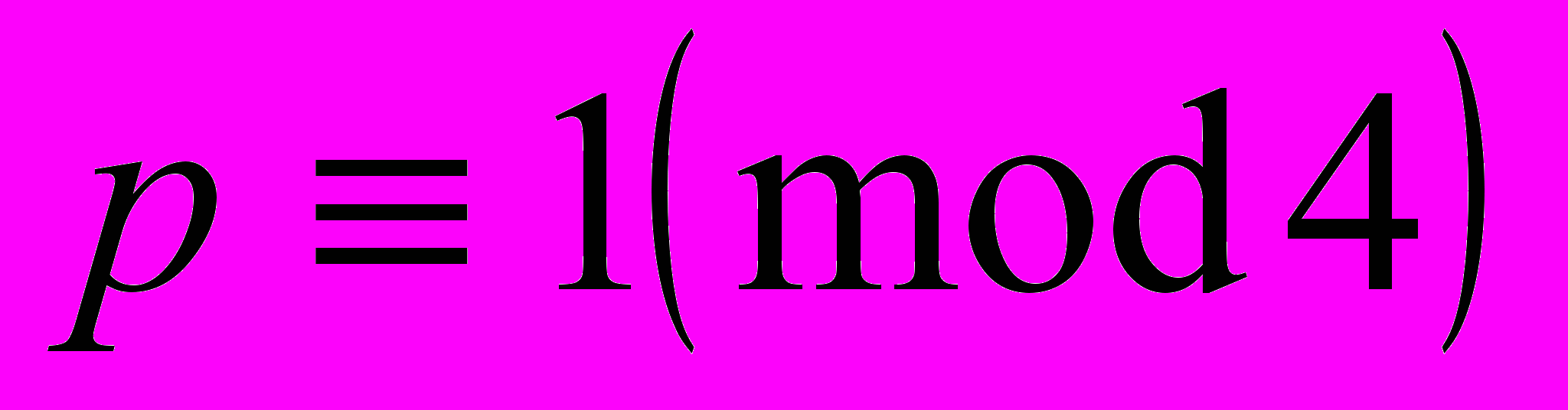 в виде суммы двух квадратов в виде суммы двух квадратовАлгебраические и трансцендентные числа. Теорема Лиувилля и ее применение к построению трансцендентных чисел и к доказательству иррациональности | 2 | | |
| Общее кол-во баллов | | | |
Посещение одного занятия – 1 балла. Учитывается количество пропусков по неуважительной причине.
Пропуск одного занятия – ( -1) балла.
Максимальное количество баллов – 9 % (9 баллов)
Минимальное – 0 %
III.
| ТЕМА ПРАКТИЧЕСКОГО ЗАНЯТИЯ | КОЛ-ВО ЧАСОВ | ПОСЕЩ-ТЬ | РАБОТА У ДОСКИ | КОЛ-ВО БАЛЛОВ |
| Тема 1. Деление с остатком. Наибольший общий делитель двух целых чисел. Алгоритм Евклида. Линейное представление наибольшего общего делителя чисел a,b в виде d=ax+by. Наименьшее общее кратное. | 2 | | | |
| Тема 2. Простые и составные числа. Признак простого числа. Решето Эратосфена. Разложение натурального числа в произведение простых множителей. Нахождение наибольшего общего делителя (наименьшего общего кратного) целых чисел по их каноническому разложению. | 2 | | | |
| Тема 3. Систематические числа. | 2 | | | |
| Тема 4. Сравнения по модулю, их основные свойства. Полная и приведенная системы вычетов. Кольцо классов вычетов. Обратимые классы. Нахождение класса вычетов, обратного данному, с помощью подходящих дробей. | 2 | | | |
| Тема 5. Сравнения по модулю, их основные свойства. Полная и приведенная системы вычетов. Кольцо классов вычетов. Обратимые классы. Нахождение класса вычетов, обратного данному, с помощью подходящих дробей. | 2 | | | |
| Тема 6. Функция Эйлера. Теоремы Эйлера и Ферма. Нахождение остатка от деления на заданное число. | 2 | | | |
| Тема 7. Сравнения с неизвестной величиной. Класс решений. Равносильные преобразования. Критерий разрешимости и число решений сравнения первой степени. Решение сравнений испытанием элементов полной системы вычетов и методом преобразования коэффициентов. | 2 | | | |
| Тема 8. Решение сравнений первой степени по формуле Эйлера, с помощью подходящих дробей. Сравнения первой степени и неопределенные уравнения. | 2 | | | |
| Тема 9. Системы сравнений первой степени. Сравнения по простому модулю. Сравнения по степени простого числа. Редукция сравнения по составному модулю к сравнению по степени простого числа и к сравнениям по простому модулю. | 2 | | | |
| Тема 10 Признаки делимости. Общий признак делимости Паскаля. Признаки делимости на 2, 3, 4, 5, 10к, 7, 11, 13 в десятичной системе счисления. Определение длины периода десятичной дроби. | 2 | | | |
| Тема 11.Порядок (показатель) числа и класса вычетов по данному модулю, его свойства. Число классов с заданным показателем по простому модулю. Нахождение первообразных корней. Индексы чисел и классов по данному простому модулю. Свойства индексов. Построение таблиц индексов. Применение индексов к решению двучленных сравнений 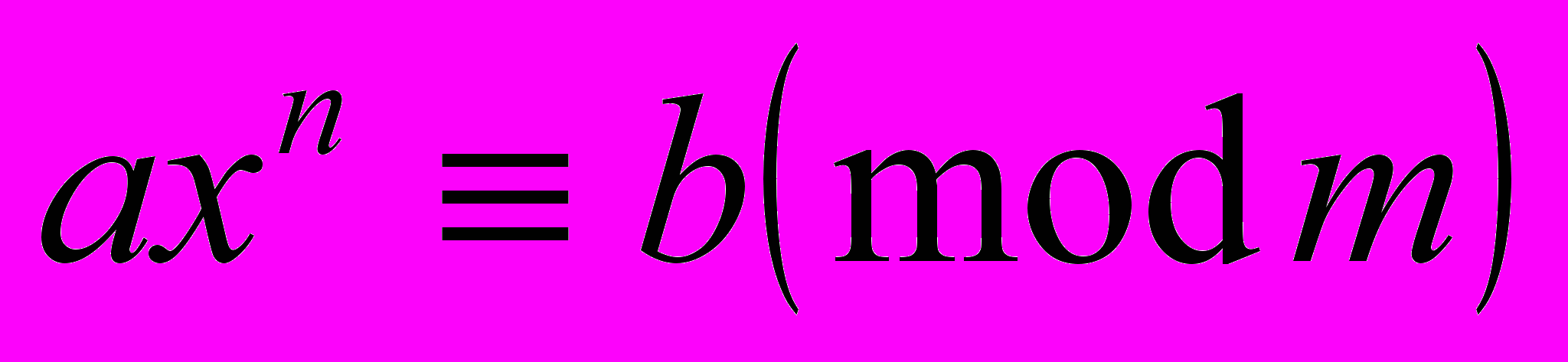 и показательных сравнений вида и показательных сравнений вида 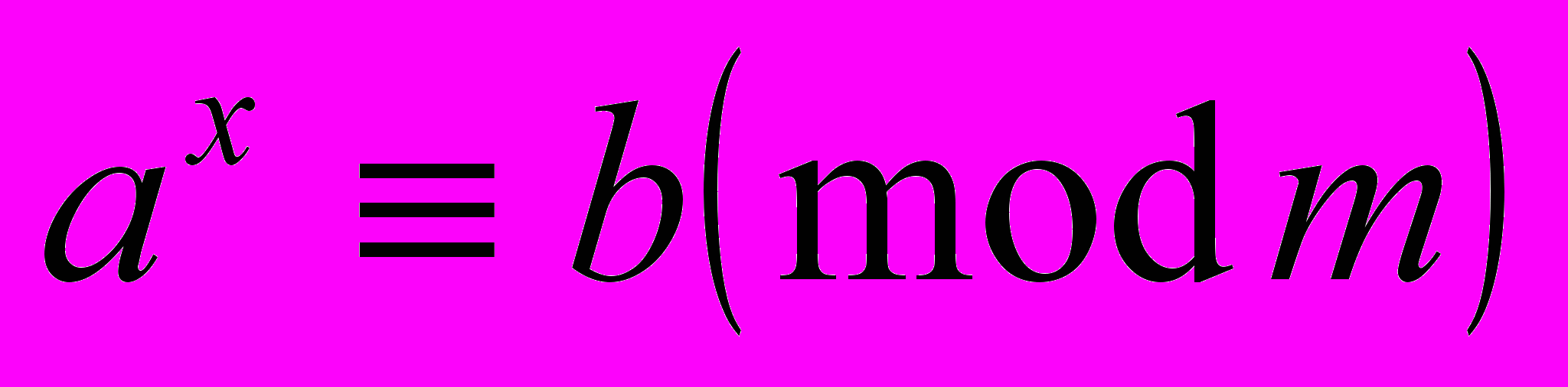 . . | 2 | | | |
| Тема 12. Квадратичные вычеты и невычеты. Критерий Эйлера. Символ Лежандра. | 2 | | | |
| Тема 13. Контрольная работа. | 2 | | | |
| Тема 14. Квадратичные иррациональности. Теорема Лагранжа. Алгебраические и трансцендентные числа. | 2 | | | |
Ответы оцениваются на каждом семинаре (максимальная оценка за практическое занятие- 1 балл (1 %)):
1. Посещаемость – 1 балл
2. Работа у доски– 1 балл
5. Отсутствие на семинарском занятии по неуважительной причине -1 балла
Максимальное количество баллов за работу на семинарских занятиях – 28% (28 баллов)
Минимальное – 0%.
IV.
| САМОСТОЯТЕЛЬНАЯ РАБОТА | КОЛ-ВО БАЛЛОВ |
| Коллоквиум №1 | |
| Коллоквиум №2 | |
| Индивидуальное задание | |
1. Коллоквиум – 10 баллов
2. Индивидуальное задание-15 баллов
Максимальное кол-во баллов за самостоятельную работу –35% (35 баллов).
| ПИСЬМЕННЫЕ РАБОТЫ | ОБЩЕЕ КОЛ-ВО БАЛЛОВ | |
| №1 | | |
| №2 | | |
| №3 | | |
Тест (максимальное количество баллов за тест – %)
Критерии оценки теста:
Оценка «отлично» - 3 %.
Оценка «хорошо» - 2%.
Оценка «удовлетворительно» - 1 %.
Оценка «неудовлетворительно» - 0 %.
Контрольная работа (максимальное количество баллов за контрольную работу – 9 %), проводится в конце семестра.
Критерии оценки:
Оценка «отлично» -9 %.
Оценка «хорошо» - 7 %.
Оценка «удовлетворительно» - 5 %.
Оценка «неудовлетворительно» - 2 %.
В конце семестра суммируются результаты 5 аспектов, входящих в рейтинговую книжку студента:
Максимальное количество баллов – 100% (отметка «отлично»)
- 75 % (отметка «хорошо»)
Минимальное количество баллов – 60 % (отметка «удовлетворительно») При условии согласия студента с оценкой студент освобождается от экзамена, если же студент претендует на более высокую оценку – он сдает экзамен. Примечание: на экзамене студент может улучшить свою оценку лишь на один балл.
3.2. КОНТРОЛЬНО-ИЗМЕРИТЕЛЬНЫЕ МАТЕРИАЛЫ
3.2.1. Текущий контроль
Вопросы к зачету
- Отношение делимости в Z, его простейшие свойства.
- Теорема о делении с остатком.
- Простые числа. Бесконечность множества простых чисел.
- Разложение целых чисел на простые множители, его единственность.
- Наибольший общий делитель двух целых чисел. Алгоритм Евклида. Свойства НОД.
- Наименьшее общее кратное двух целых чисел.
- Цепные дроби. Свойства подходящих дробей.
- Сравнения по модулю, их основные свойства.
- Полная и приведенная системы вычетов по модулю т.
- Мультипликативная группа классов вычетов, взаимно простых с модулем.
- Поле классов вычетов по простому модулю.
- Кольцо классов вычетов по модулю т.
- Функция Эйлера. Теоремы Эйлера и Ферма.
- Сравнения первой степени с одной переменной.
- Порядок числа и класса вычетов по модулю.
- Первообразные корни. Существование первообразных корней по простому модулю.
- Индексы по простому модулю. Свойства индексов. Таблицы индексов, их применение.
- Понятие о степенных вычетах. Квадратичные вычеты и невычеты. Символ Лежандра.
- Представление действительных чисел цепными дробями.
- Теорема Лежандра о квадратичной иррациональности.
- Признаки делимости.
- Обращение обыкновенной дроби в десятичную. Длина периода десятичной периодической дроби.
3.2.2. Итоговый контроль
Образцы индивидуального задания
Вариант 1
- Доказать, что для любого натурального п
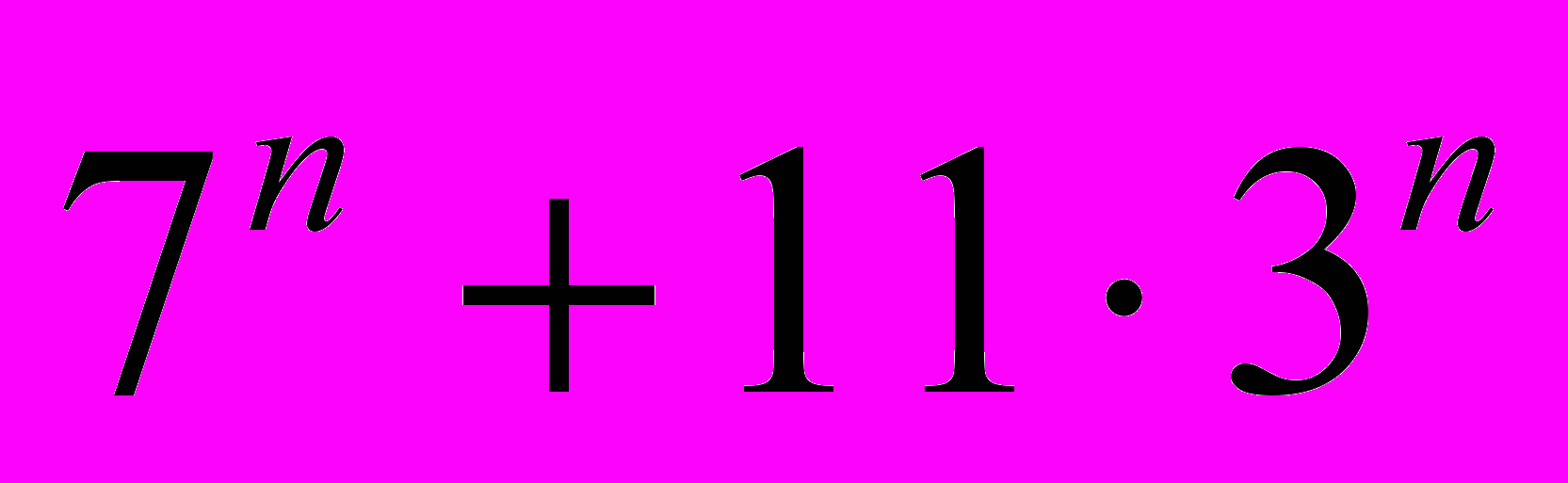 кратно 4.
кратно 4.
- Найти НОД
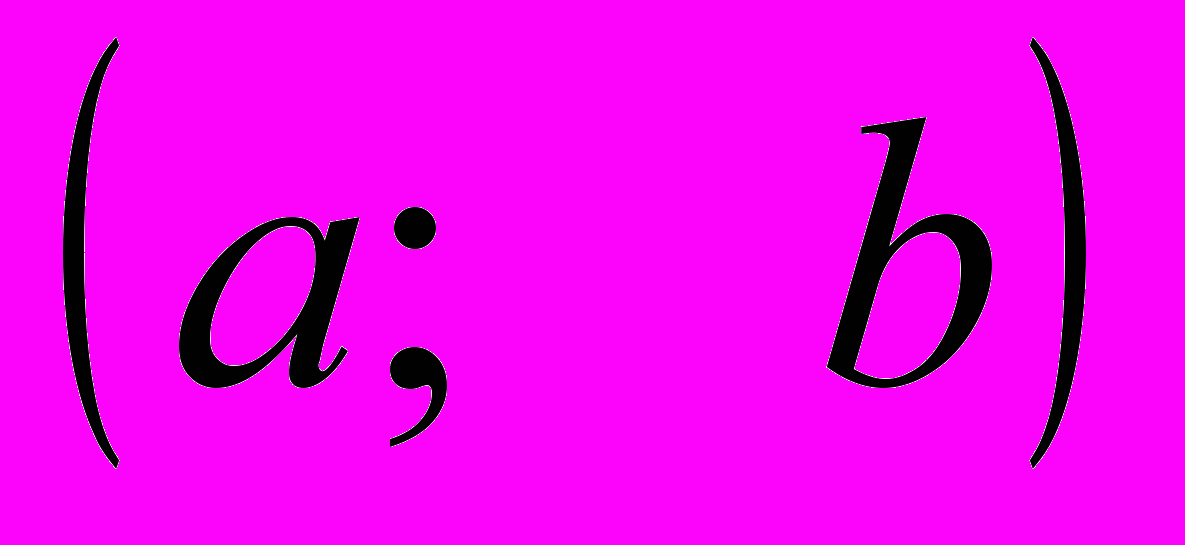 , НОК
, НОК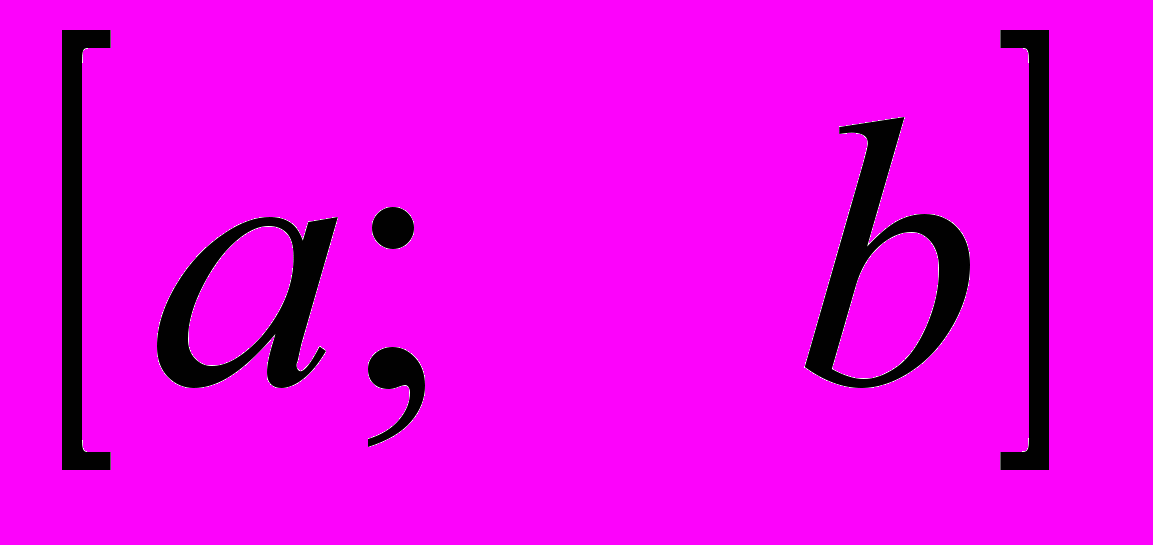 , выразить наибольший общий делитель через а и b.
, выразить наибольший общий делитель через а и b. 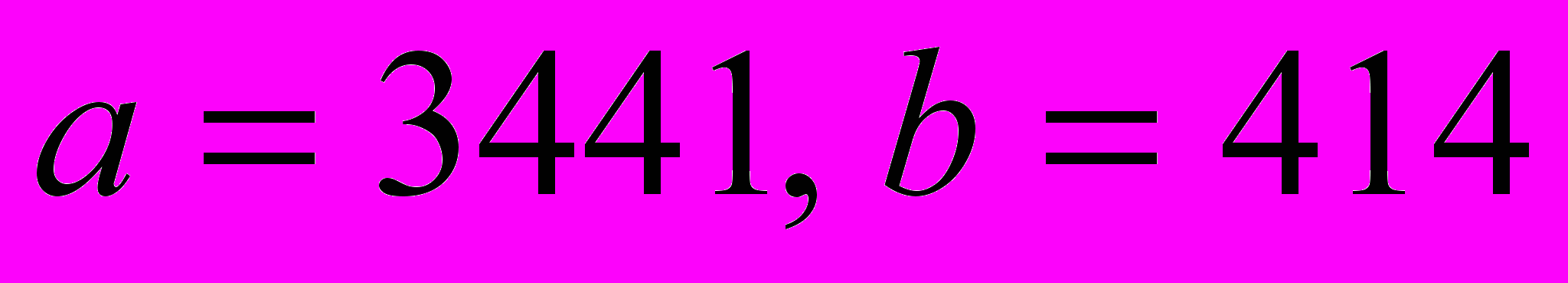 .
.
- Решить сравнения (использовать метод преобразования коэффициентов, формулу Эйлера, подходящие дроби).
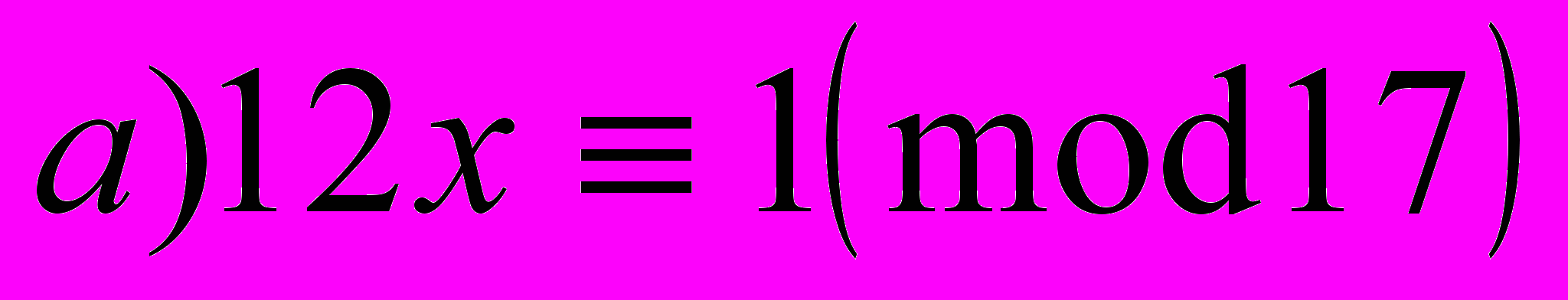
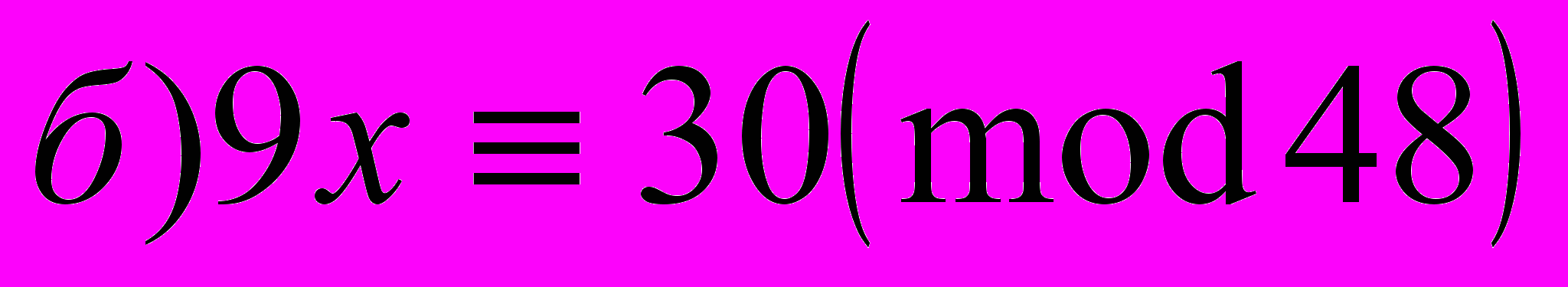 .
.- Решить уравнение с помощью сравнений (с помощью подходящих дробей)
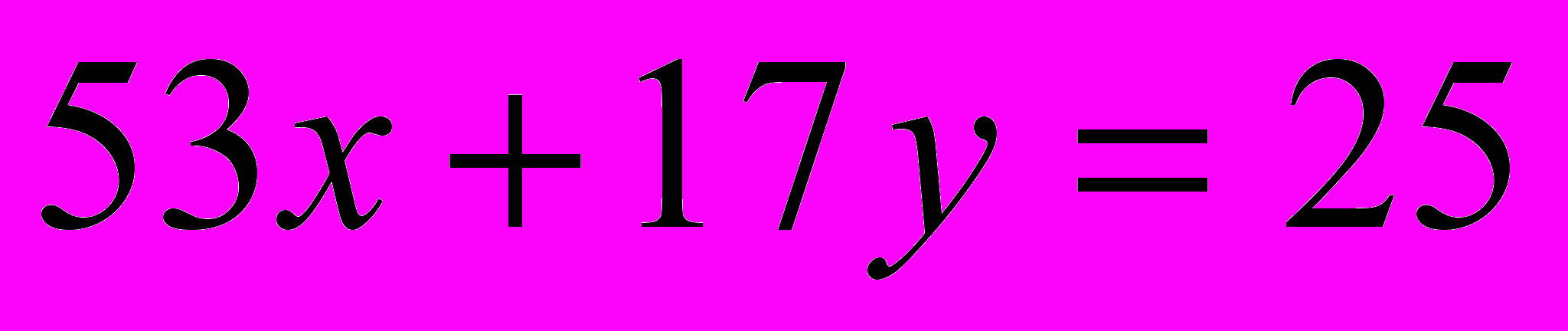 .
.
- Найти остаток от деления
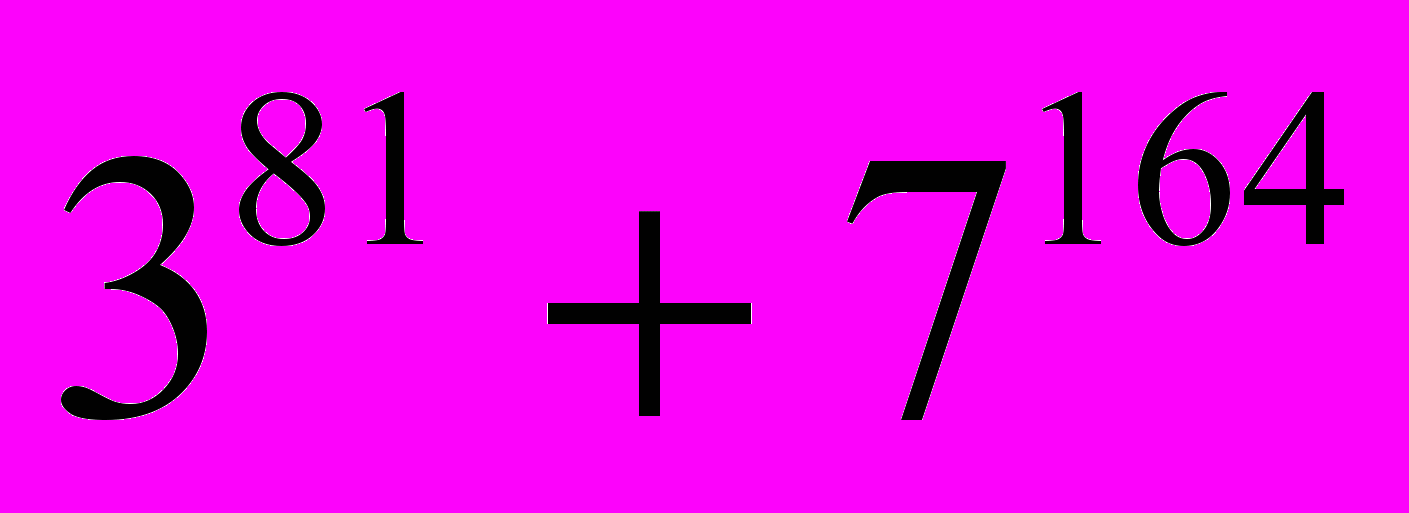 на 25.
на 25.
- Найти порядок класса вычетов
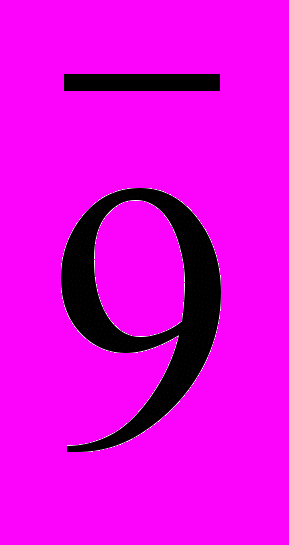 по модулю 19. Какие еще классы вычетов по модулю 19 имеют тот же порядок?
по модулю 19. Какие еще классы вычетов по модулю 19 имеют тот же порядок?
- Разложить в цепную дробь
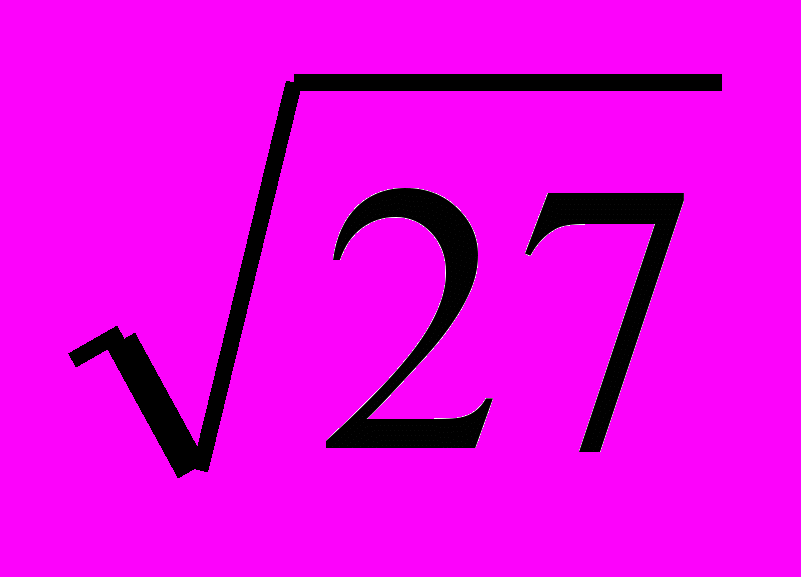 и заменить ее подходящей дробью с точностью до 0,001.
и заменить ее подходящей дробью с точностью до 0,001.
- Найти действительное число, которое обращается в цепную дробь
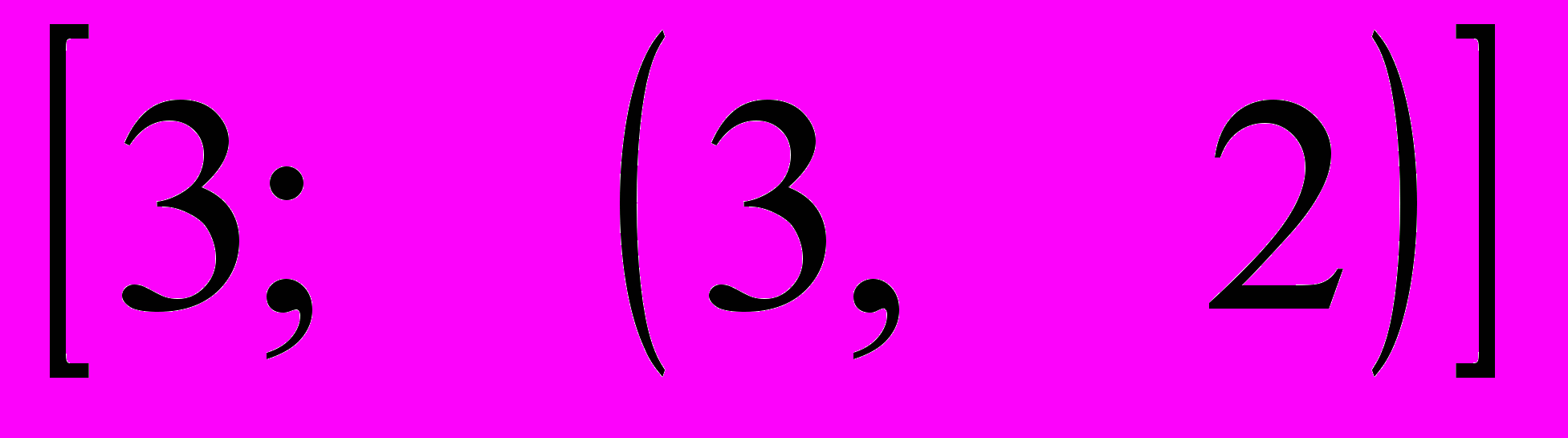 .
.
- Выбрать простые числа из отрезка натурального ряда от 610 до 650.
- Решить систему сравнений:
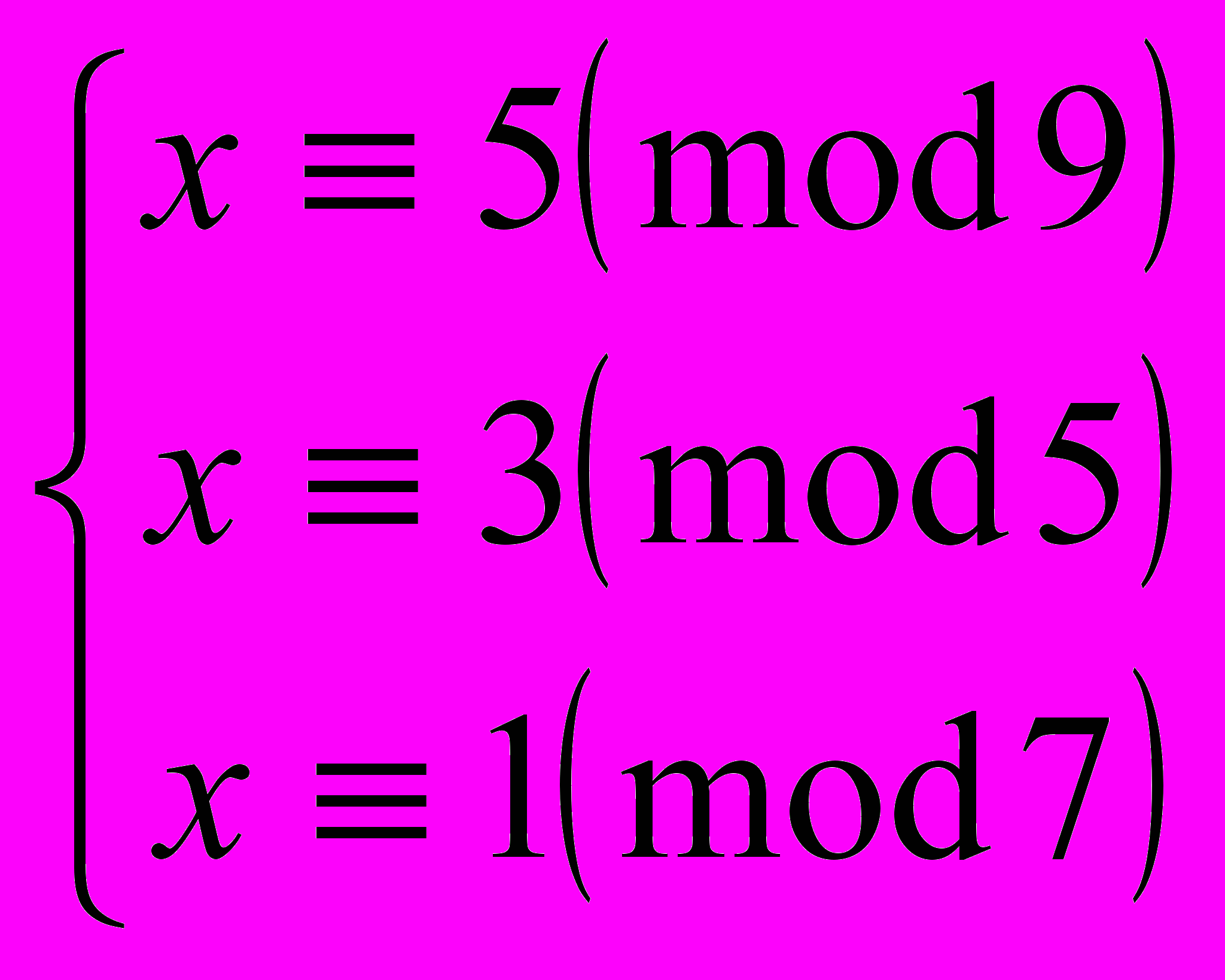
Вариант 2
- Доказать, что для любого натурального п
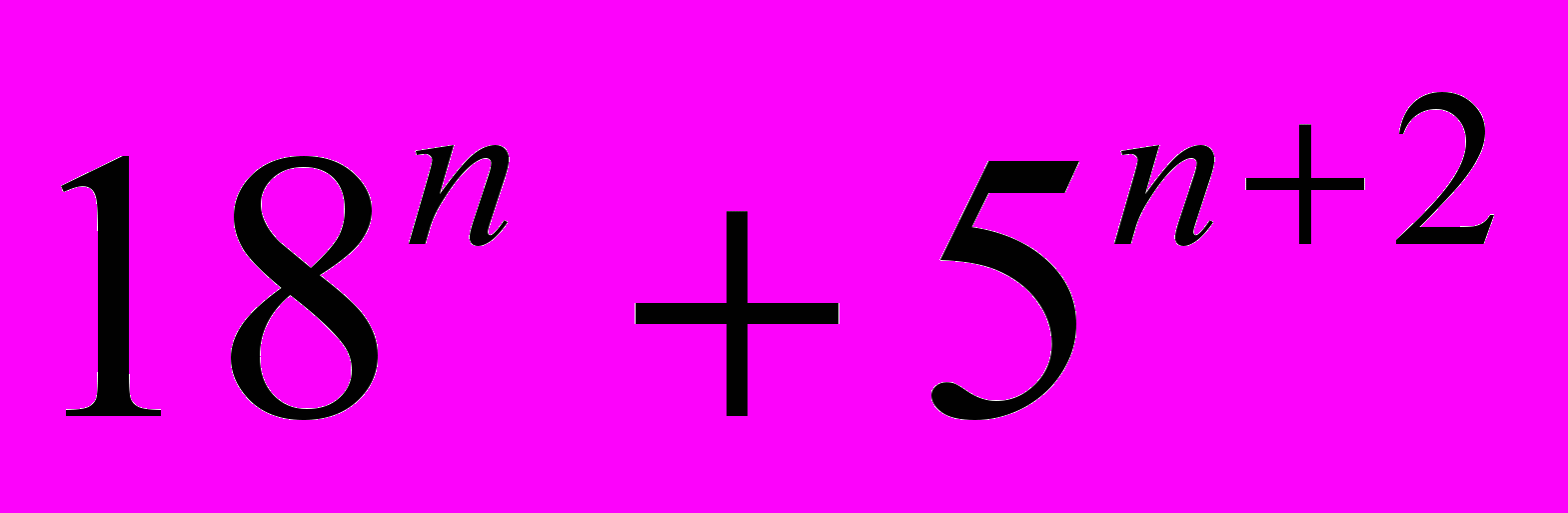 кратно 13.
кратно 13.
- Найти НОД
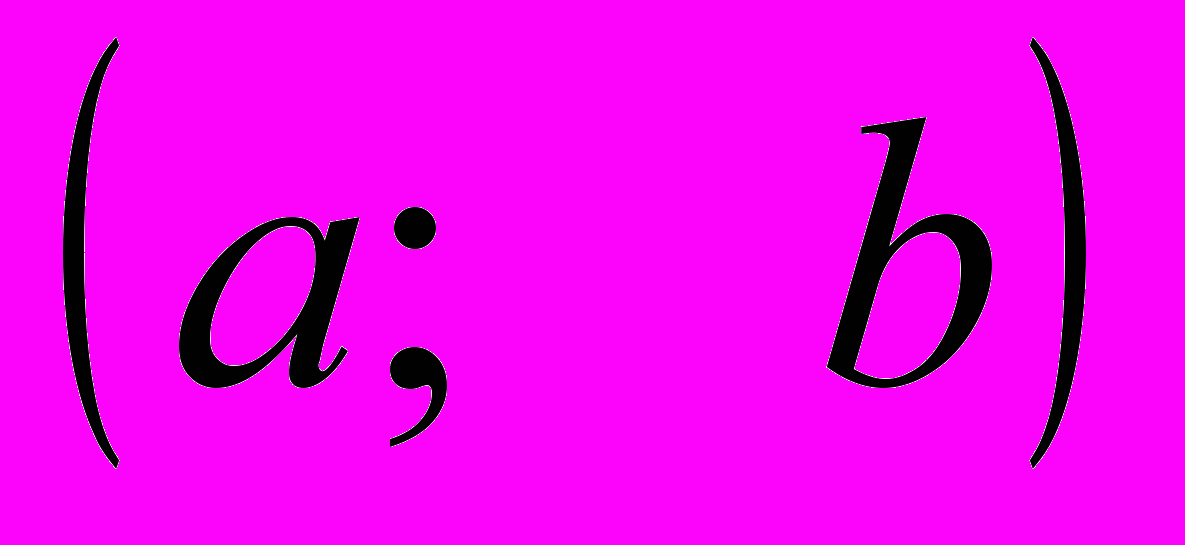 , НОК
, НОК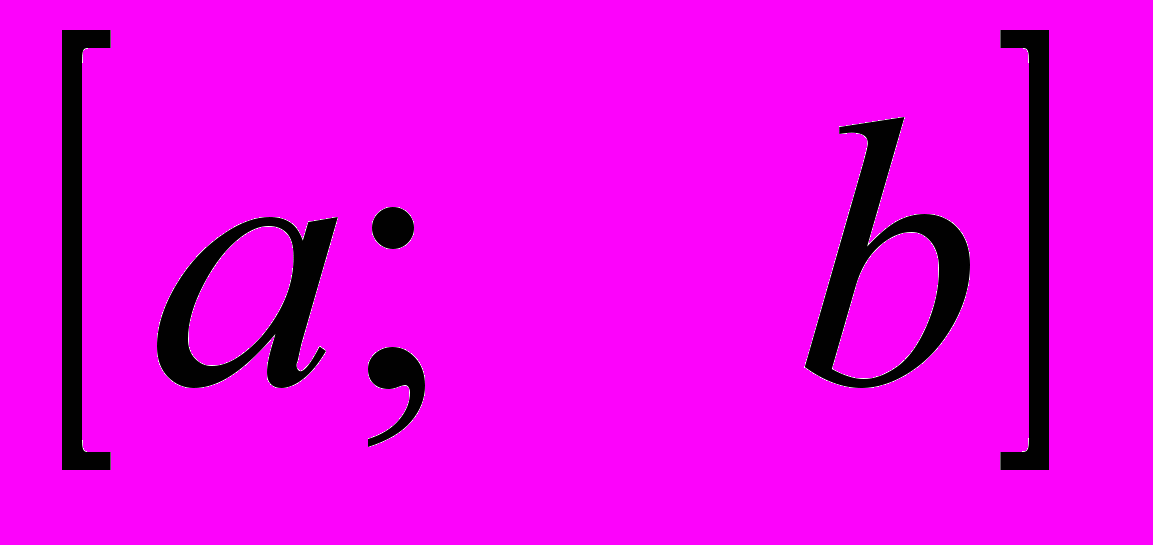 , выразить наибольший общий делитель через а и b.
, выразить наибольший общий делитель через а и b. 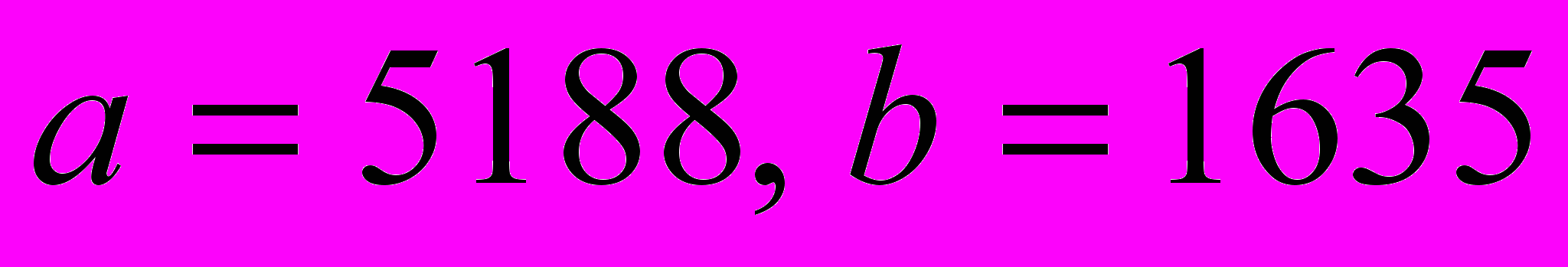 .
.
- Решить сравнения (использовать метод преобразования коэффициентов, формулу Эйлера, подходящие дроби).
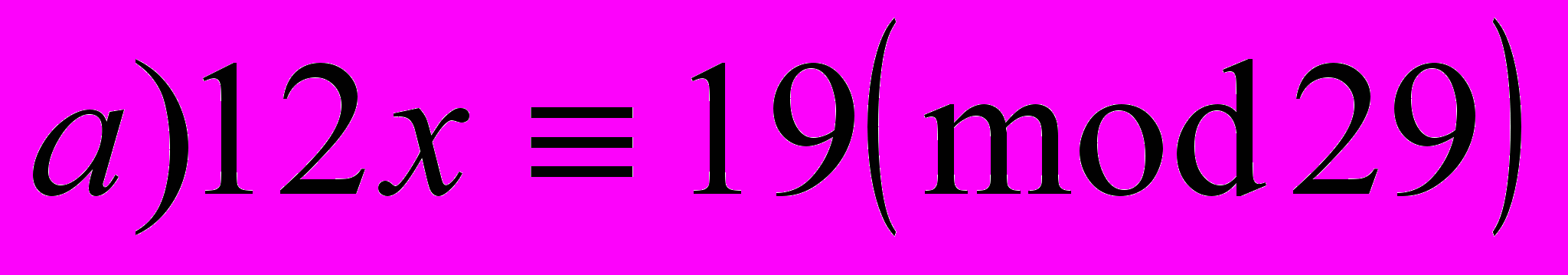
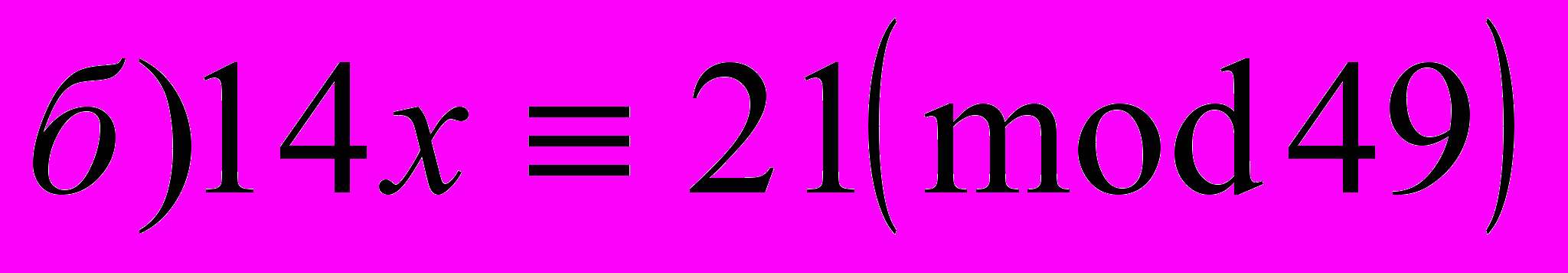 .
.- Решить уравнение с помощью сравнений (с помощью подходящих дробей)
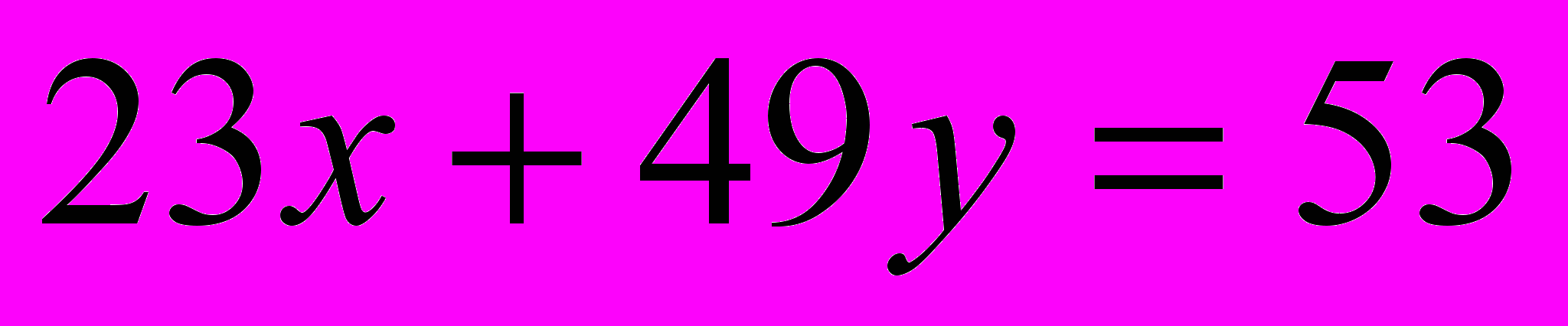 .
.
- Найти остаток от деления
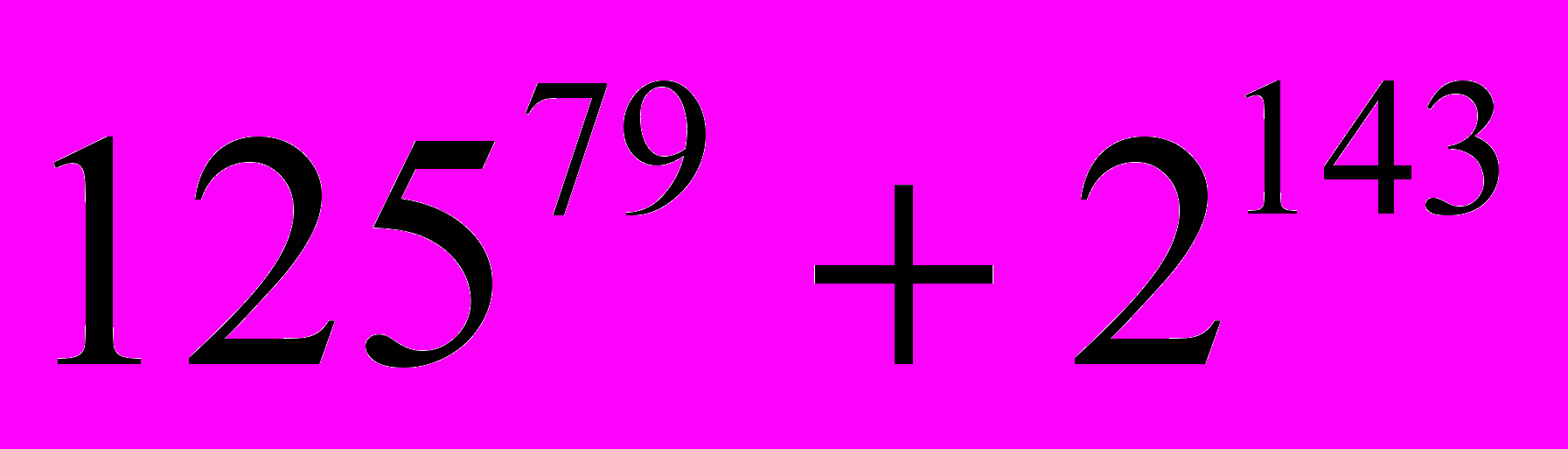 на 34.
на 34.
- Найти порядок класса вычетов
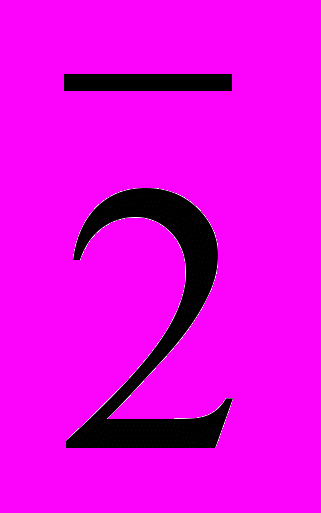 по модулю 17. Какие еще классы вычетов по модулю 17 имеют тот же порядок?
по модулю 17. Какие еще классы вычетов по модулю 17 имеют тот же порядок?
- Разложить в цепную дробь
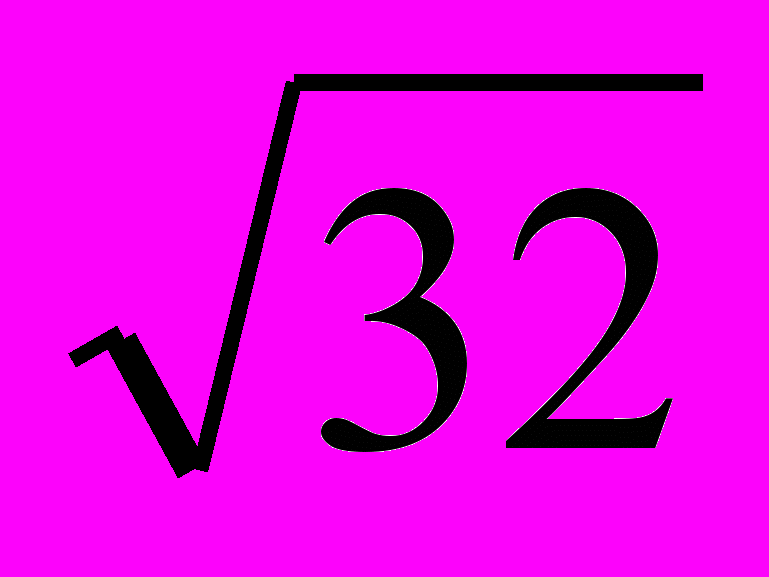 и заменить ее подходящей дробью с точностью до 0,001.
и заменить ее подходящей дробью с точностью до 0,001.
- Найти действительное число, которое обращается в цепную дробь
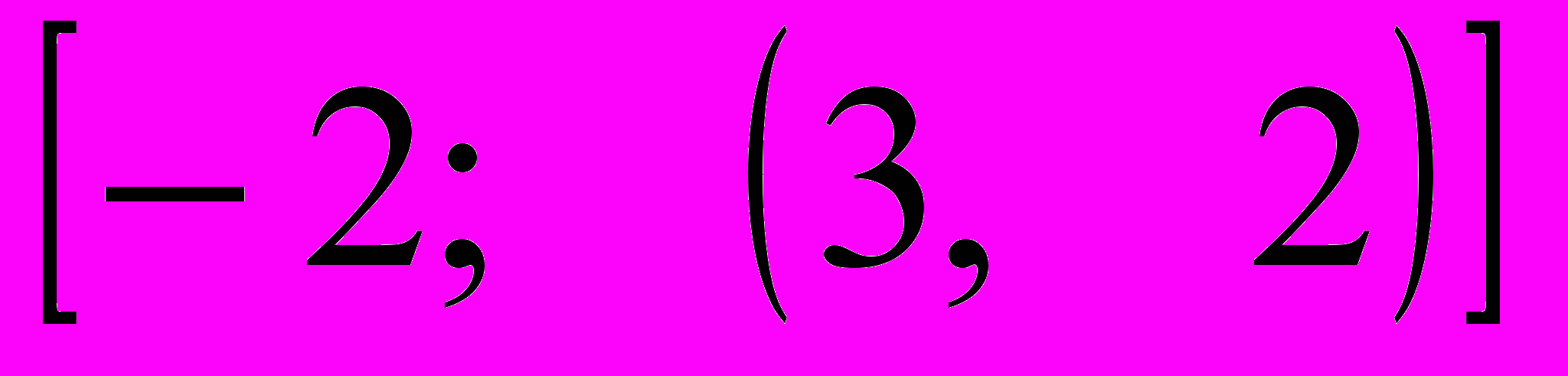 .
.
- Выбрать простые числа из отрезка натурального ряда от 570 до 610.
- Решить систему сравнений:
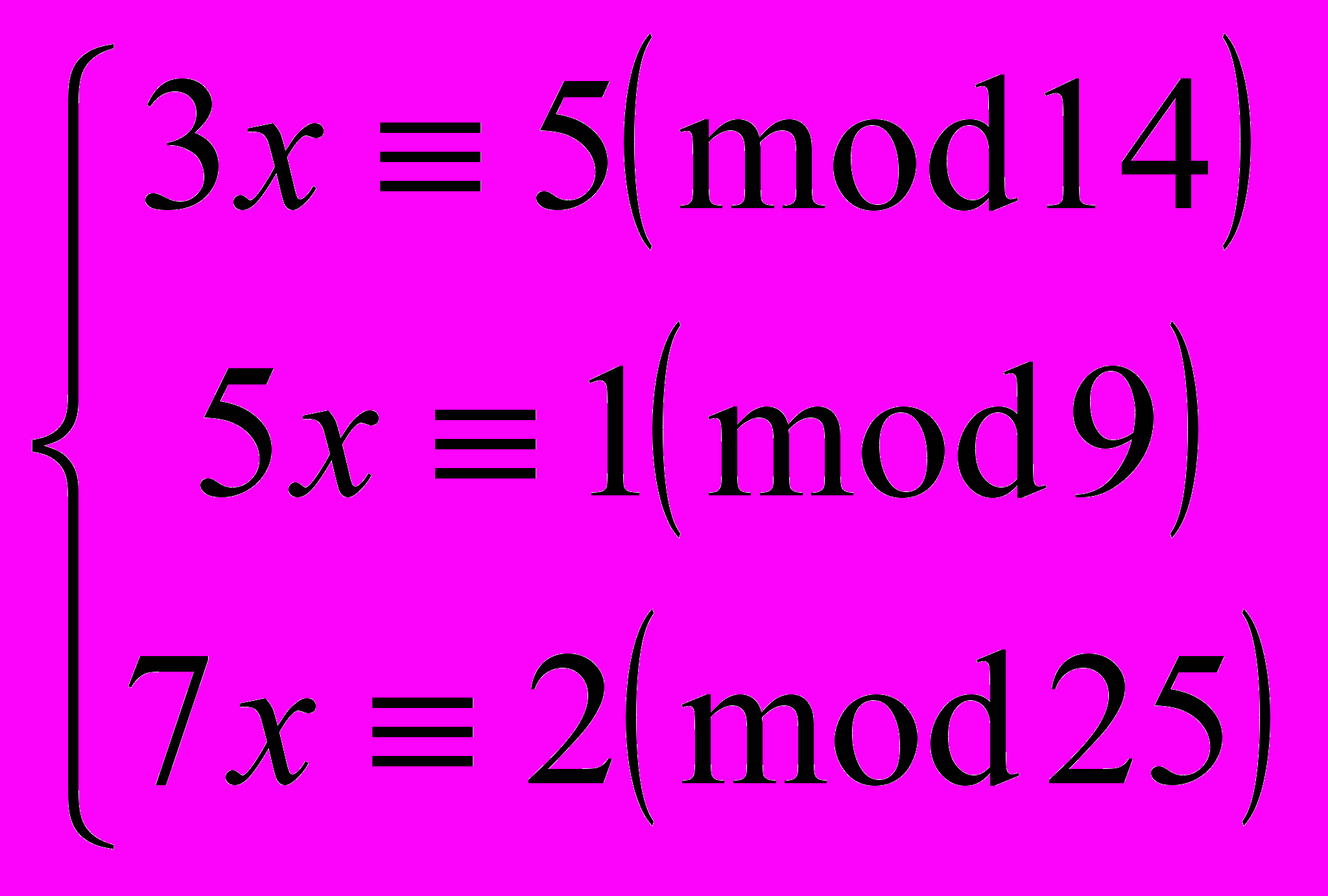
Образцы контрольных работ
Контрольная работа №1
Вариант 1
- Доказать (двумя способами) (
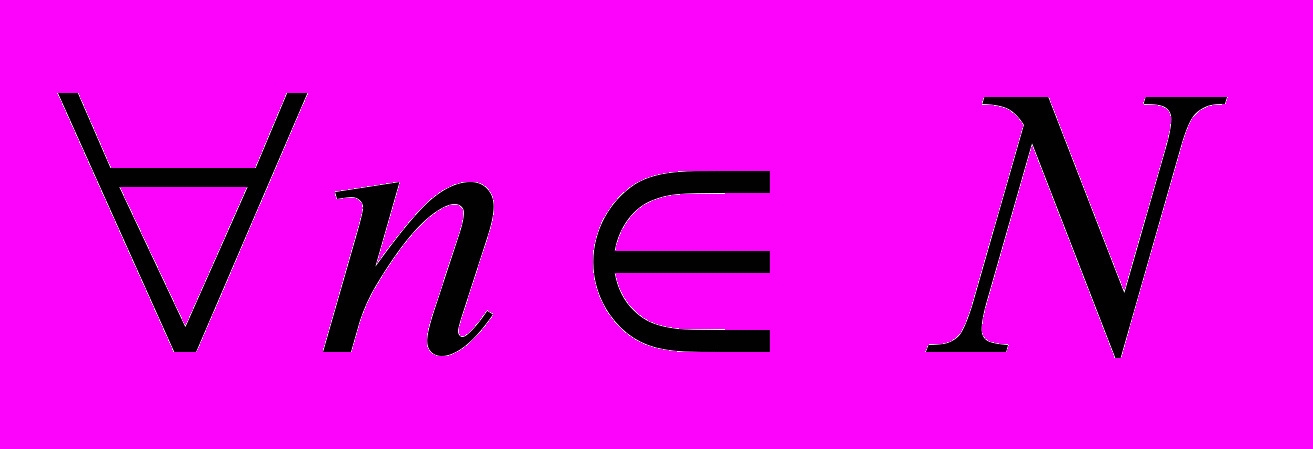 ) (
) (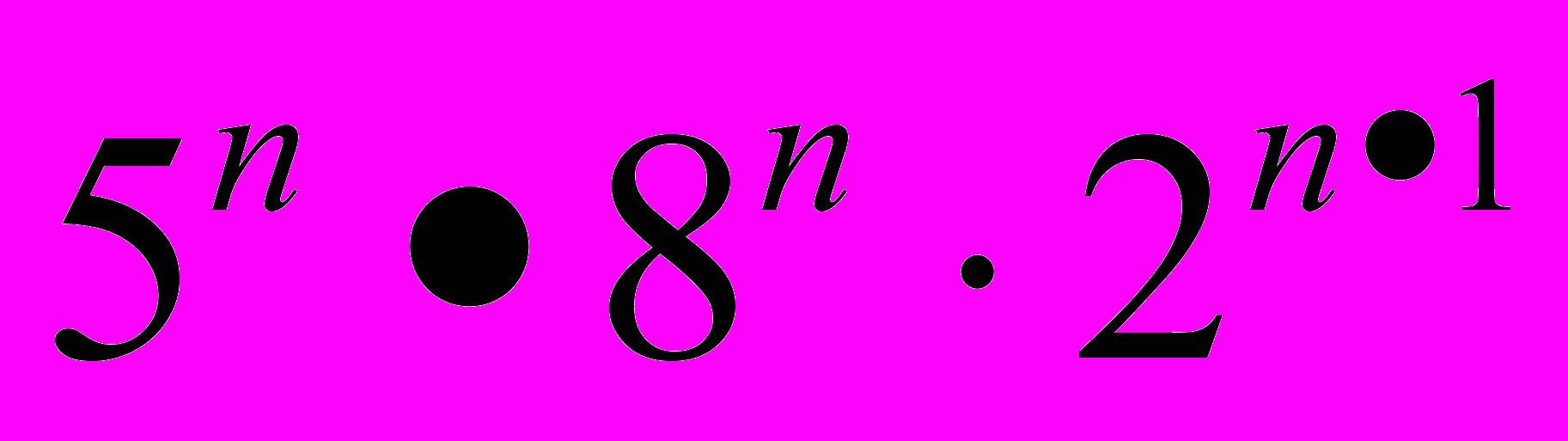 )
)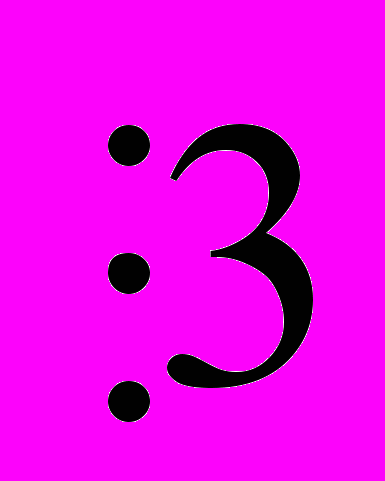 .
.
- Найти наибольший общий делитель чисел а=3731, b=2988 b =2988 и выразить его через а и b.
- Выбрать простые числа из отрезка натурального ряда от 1000 до 1050.
- Найдите двузначное число, равное утроенному произведению его цифр.
- Сократить с помощью разложения в непрерывную дробь
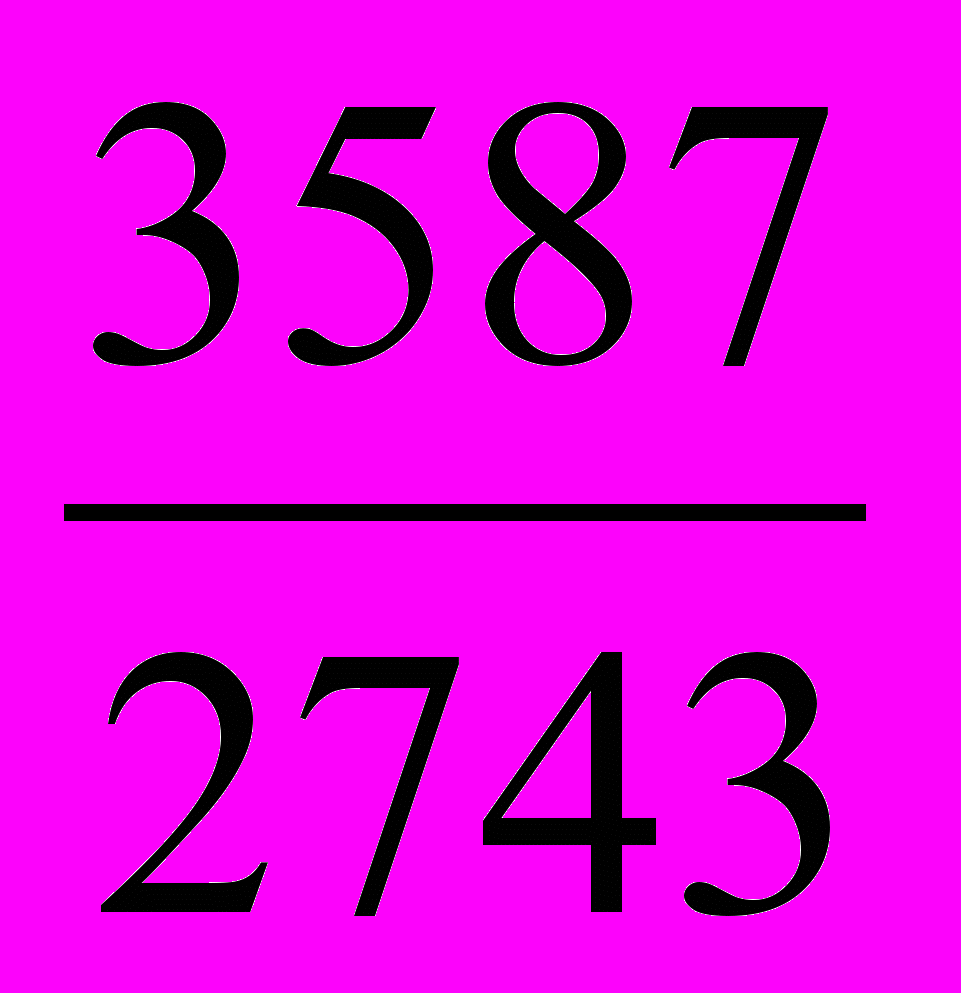 .
.
Вариант 2
- Доказать (двумя способами) (
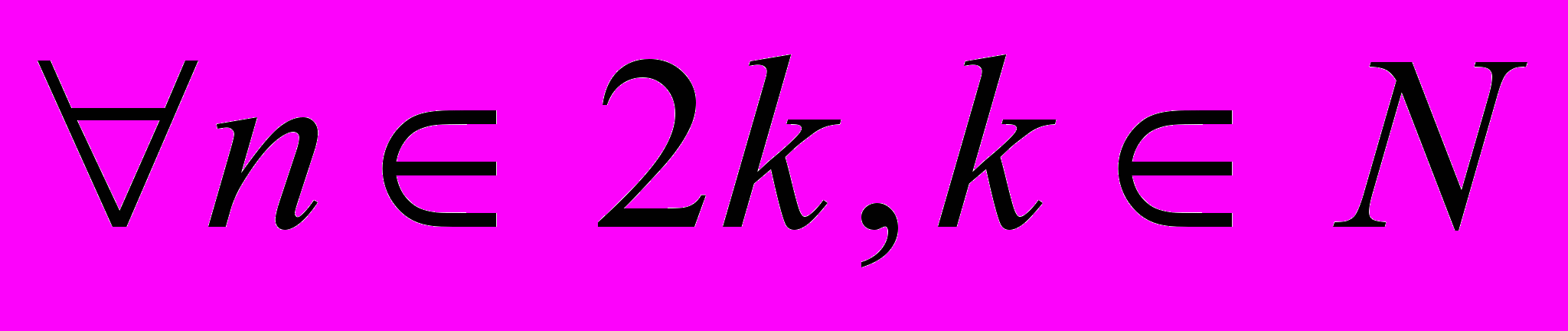 ) (
) (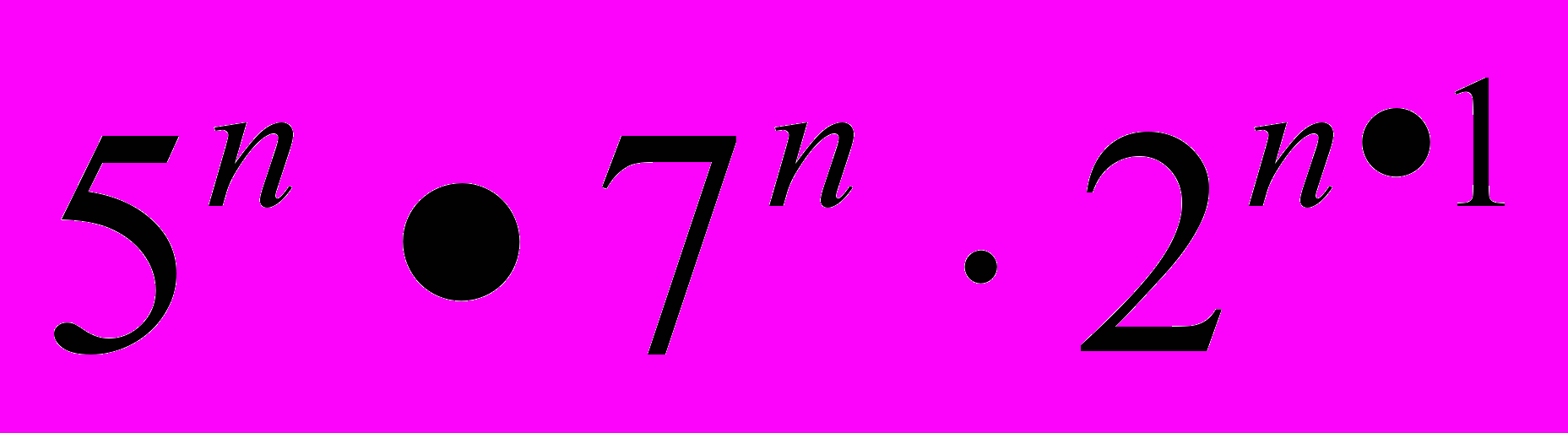 )
)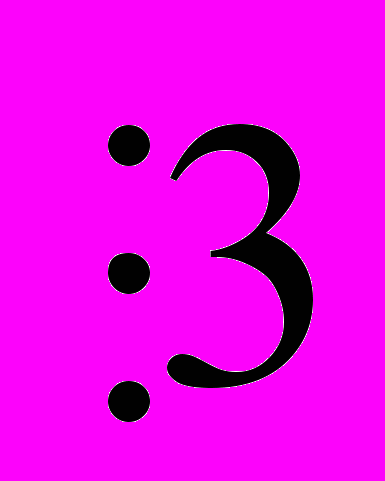
- Найти наибольший общий делитель чисел а=836, b=2988 b =111 и выразить его через а и b.
- Выбрать простые числа из отрезка натурального ряда от 1050 до 1100
- Докажите, что не существует трехзначного числа, частное от деления которого на сумму его цифр равно13, а остаток равен 23.
- Сократить с помощью разложения в непрерывную дробь
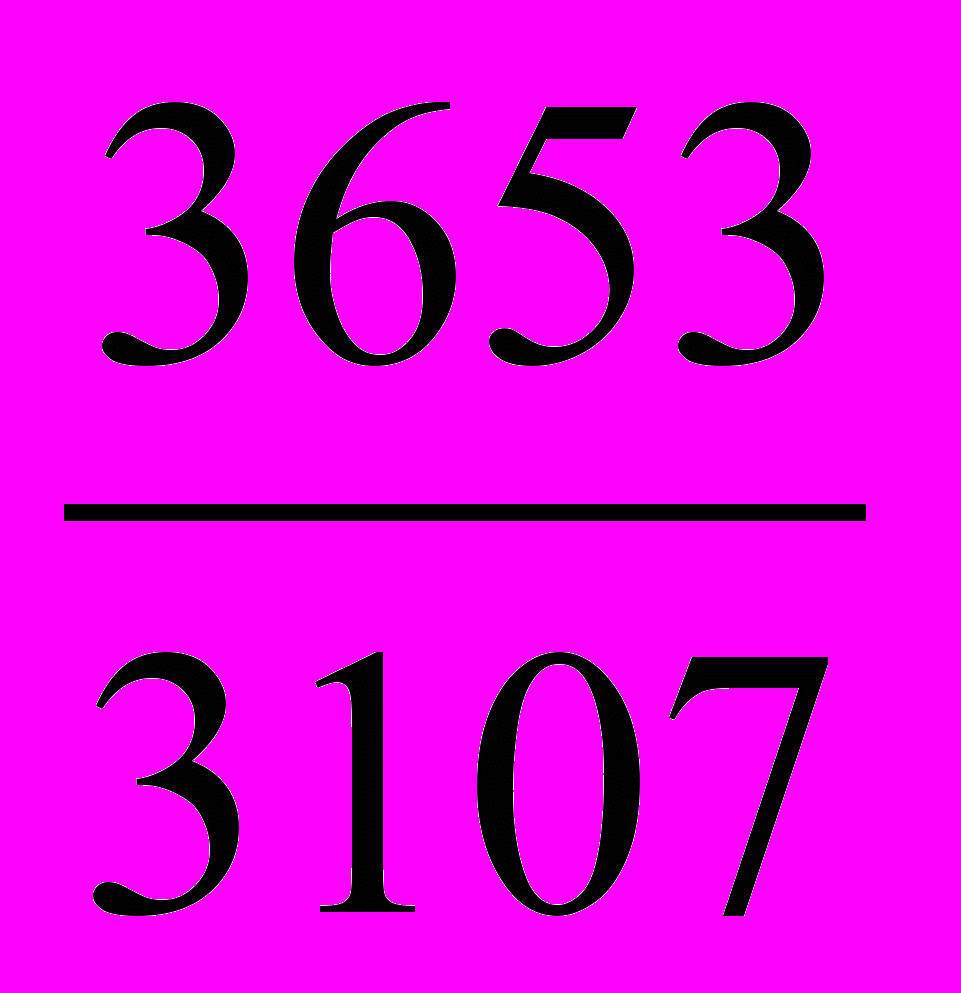 .
.
Контрольная работа №2
Вариант 1
- Составить сравнение по модулю 21, имеющее три решения.
- Решить сравнение
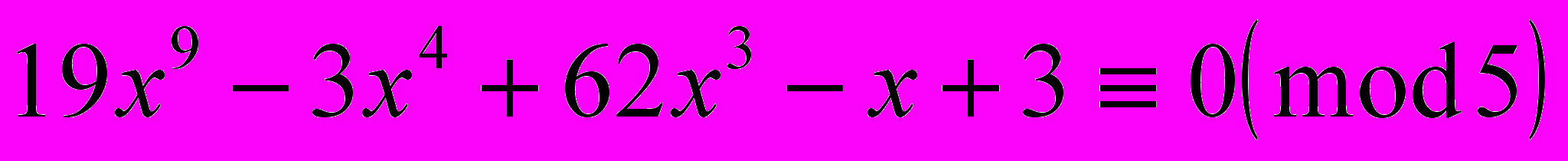
- Решить сравнения:
а)
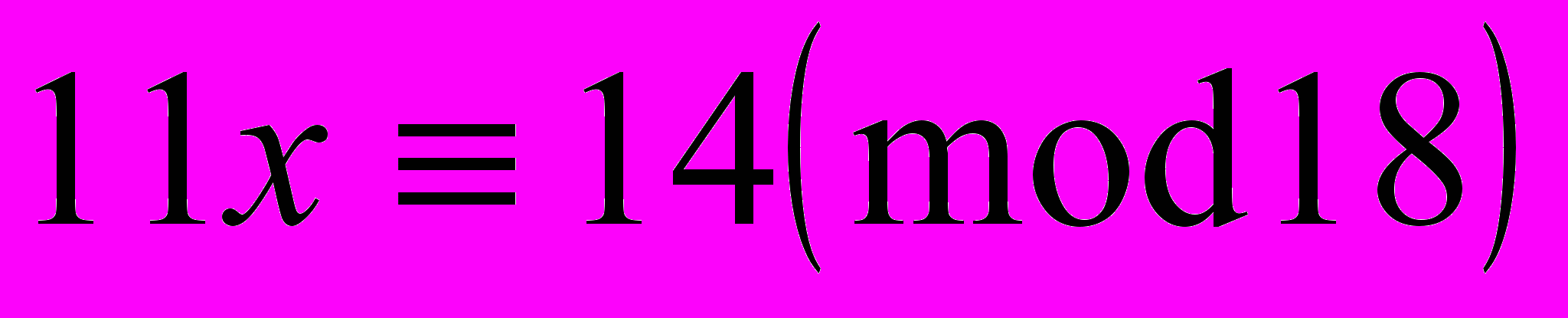
б)
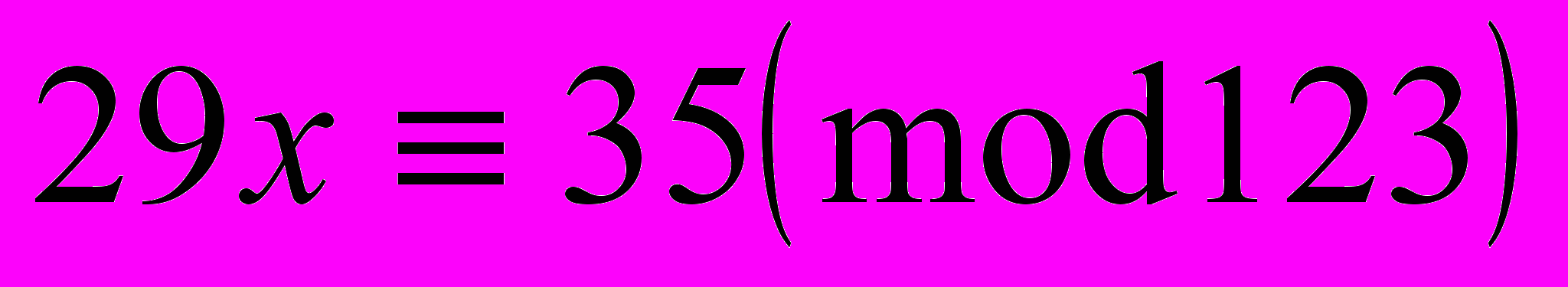
в)
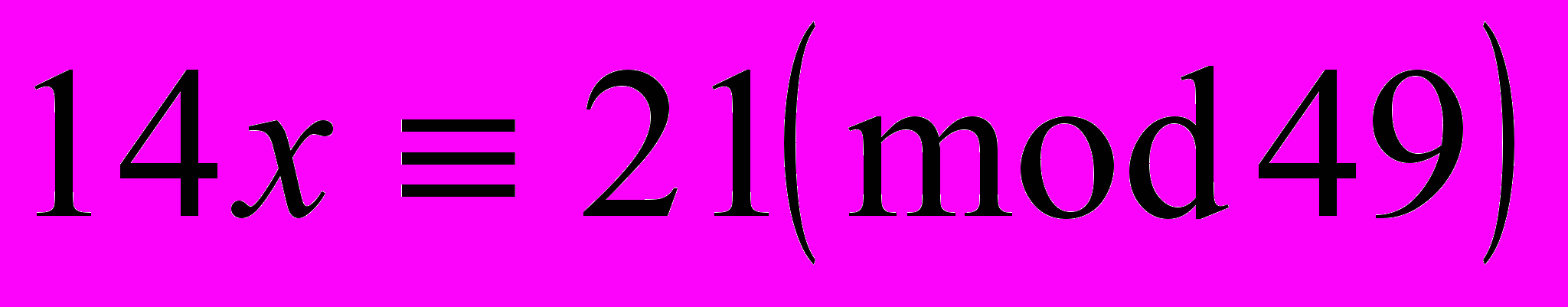
4. Решить уравнение :
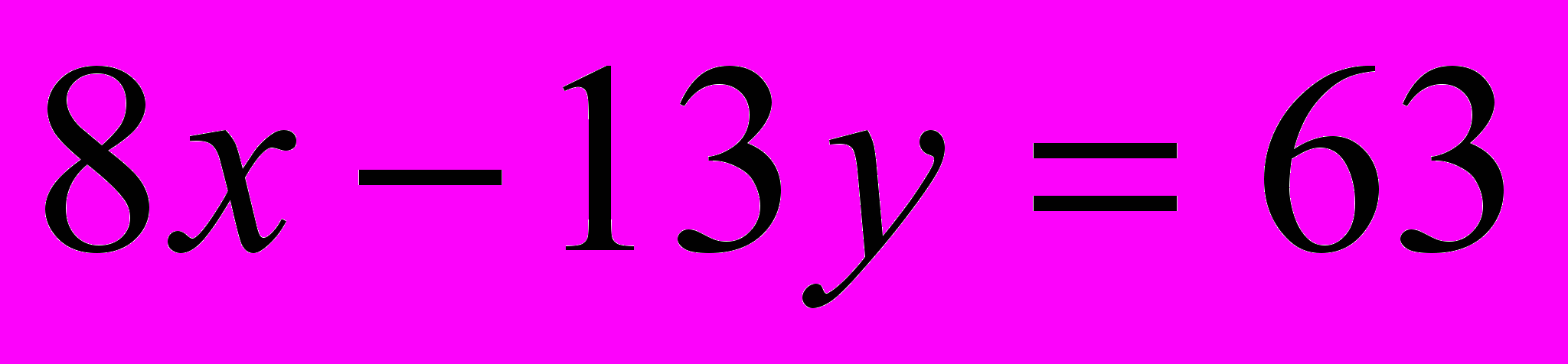 ;
;5. Решить систему:
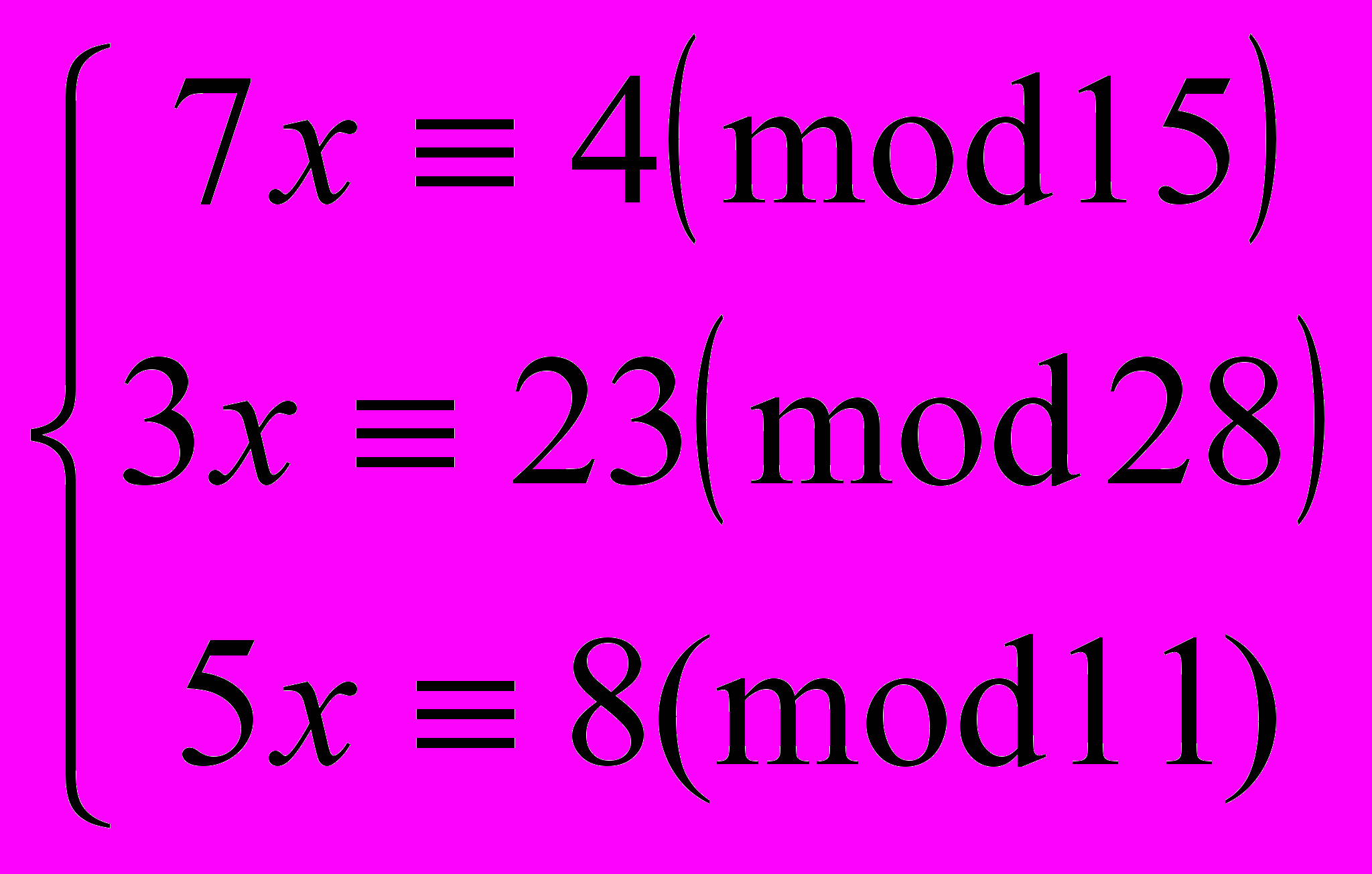
Вариант 2
1. Составить сравнение по модулю 21, не имеющее решений.
2. Решить сравнение
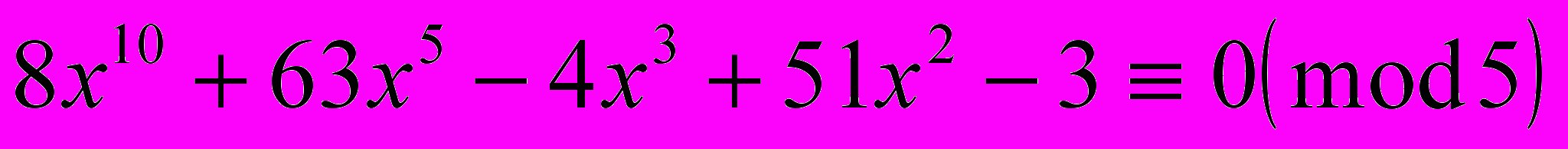
3. Решить сравнения:
а)
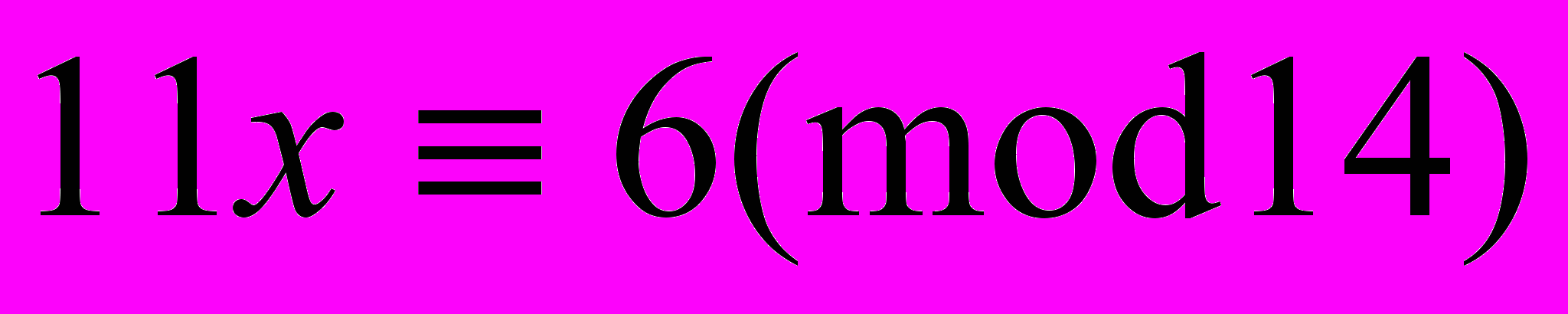
б)
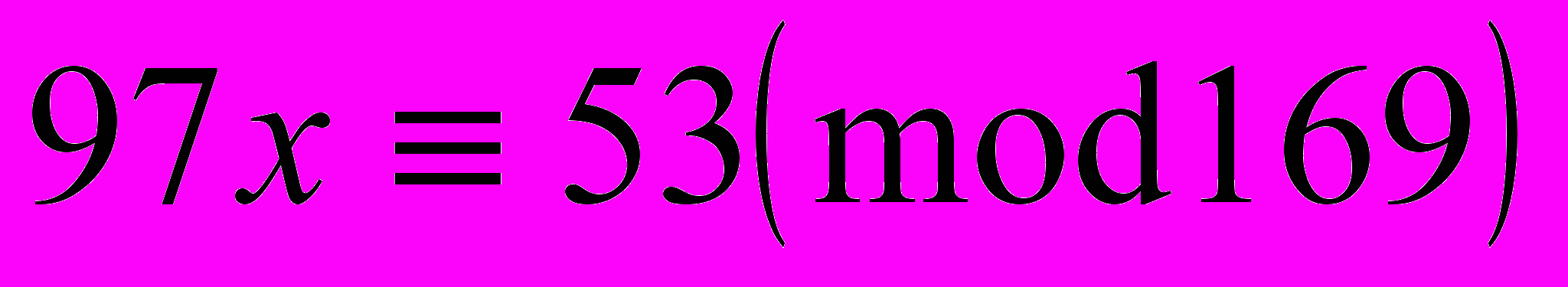
в)
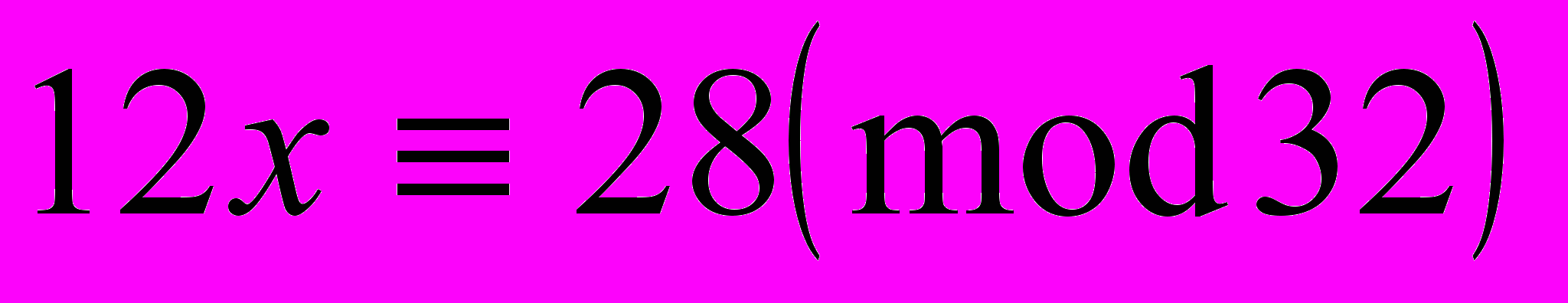
4. Решить уравнение: 16x+19y=7.
5. Решить систему:
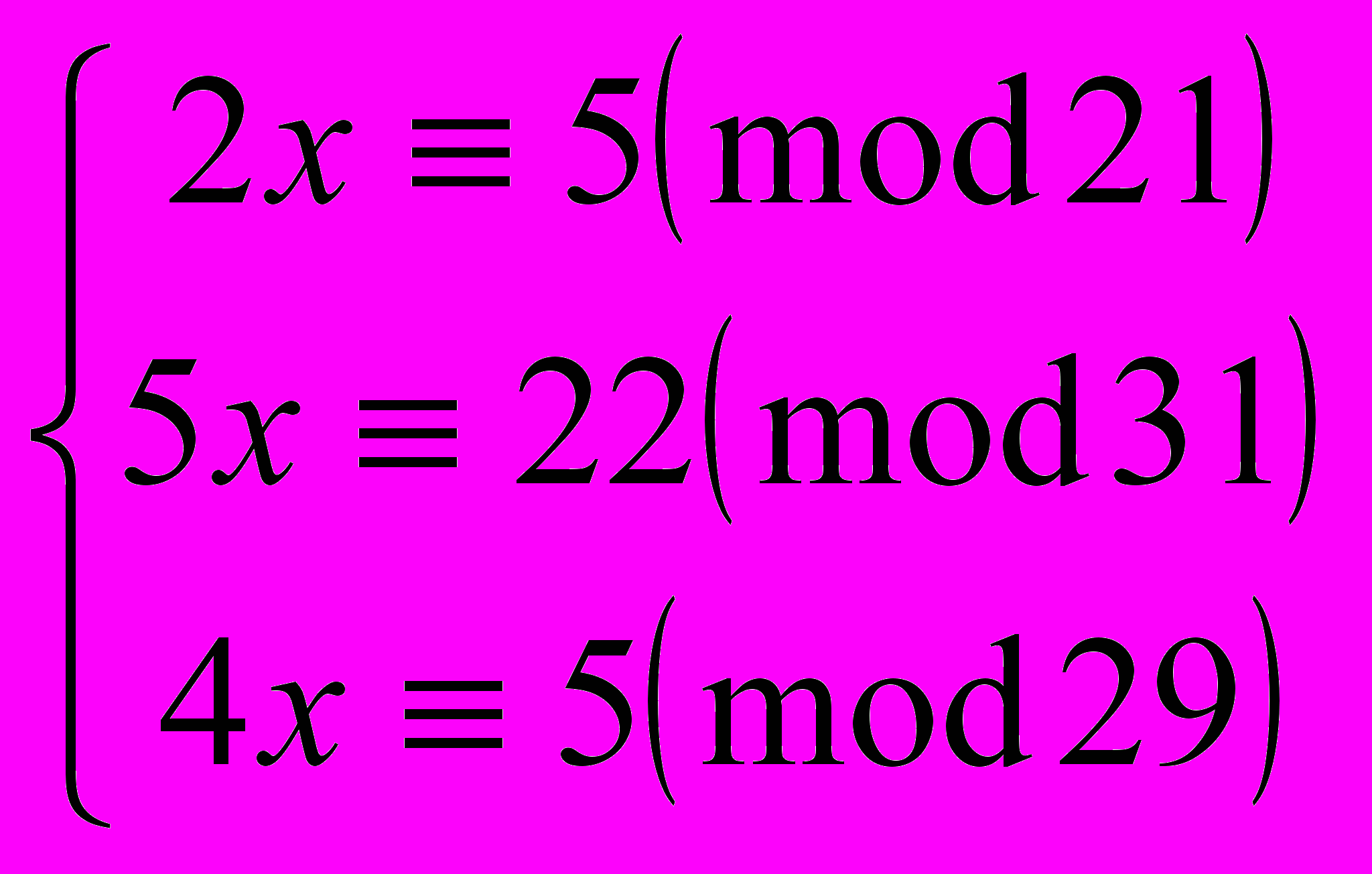

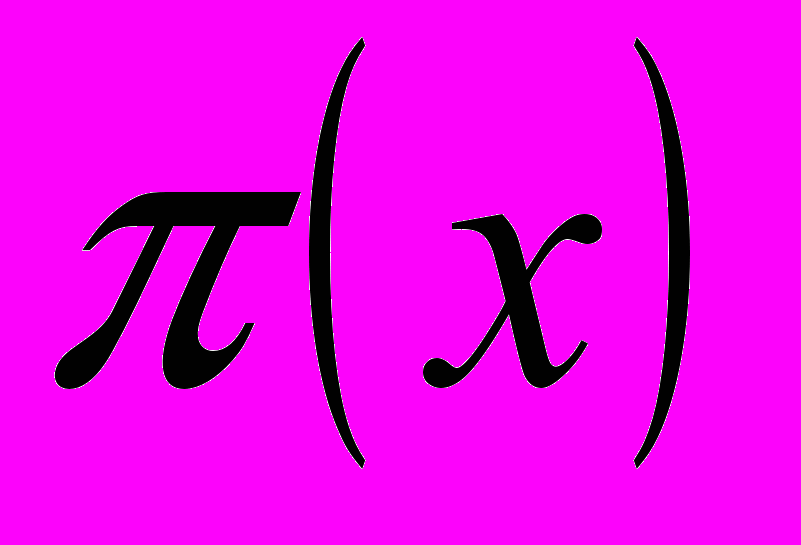 .
.