Geum.ru

Учебно-методический комплекс дисциплины Бийск бпгу имени В. М. Шукшина

Вид материалаУчебно-методический комплекс

Содержание


4. Методические рекомендации
2.1. Лекционный курс (18 часов)
2.2. Практические ЗАНЯТИЯ (28 часов)
Литература и задания
2.3. САМОСТОЯТЕЛЬНАЯ РАБОТА СТУДЕНТОВ (44 часа)
4. Учебно-методическая карта
Номер недели
Подобный материал:
1   2   3   4

4. МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ

4.1. Методические рекомендации для студентов


4.2. Методические рекомендации для преподавателей


2.1. Лекционный курс (18 часов)


№
Содержание лекции
часы
Литература


1
Делимость целых чисел. Теорема о делении с остатком. Наибольший общий делитель. Наименьшее общее кратное.

Простые и составные числа. Свойства простых чисел. Признак простоты числа. Основная теорема арифметики.

Бесконечность множества простых чисел. Неравенство Чебышева для .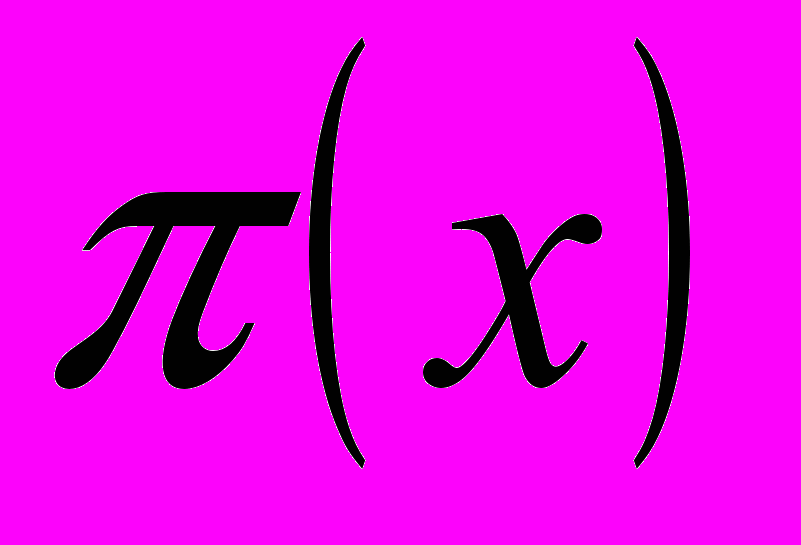


2

(1),

(2),

(3),

(4)


2
Конечные цепные дроби. Разложение рационального числа в конечную цепную дробь. Подходящие дроби. Свойства подходящих дробей.

2
(1), (2),

(3), (4)


3
Сравнения по модулю, их основные свойства. Кольцо классов вычетов. Полная и приведенная системы вычетов.

Мультипликативная группа обратимых элементов в кольце классов вычетов. Поле классов вычетов по простому модулю. Функция Эйлера. Теоремы Эйлера и Ферма.

2

(1), (2),

(3), (4)


4
Сравнения с неизвестной величиной. Сравнения первой степени. Критерий разрешимости и число решений. Решение методом подбора, методом преобразования коэффициентов, по формуле Эйлера, с помощью подходящих дробей.

2

(1), (2),

(3), (4)


5
Сравнения по простому модулю. Сведение к наиболее простому виду. Максимальное число решений. Теорема Вильсона. Сравнения по степени простого числа. Редукция сравнения по составному модулю к сравнению по степени простого числа и к сравнениям по простому модулю.

2

(1), (2),

(3), (4)


6
Показатели чисел и классов по данному простому модулю. Число классов с заданным показателем. Теорема о существовании первообразного корня по простому модулю.

Индексы чисел и классов по данному модулю. Основные свойства индексов. Таблицы индексов. Применение индексов к решению двучленных сравнений по простому модулю. Квадратичные вычеты и невычеты. Символ Лежандра.

2

(1), (2),

(3), (4)

7
Арифметические приложения теории сравнений. Вычисление остатков при делении на данное число. Признаки делимости. Определение длины периода, получающегося при обращении обыкновенной дроби в десятичную.

2

(1), (2),

(3), (4)


8
Бесконечные цепные дроби. Сходимость бесконечных цепных дробей. Разложение действительных чисел в цепные дроби. Квадратичные иррациональности и периодические цепные дроби. Теорема Лагранжа о квадратичной иррациональности.

2

(1), (2), (4)


9
Приближение действительных чисел подходящими дробями. Теорема Дирихле, ее применение к представлению простого числа 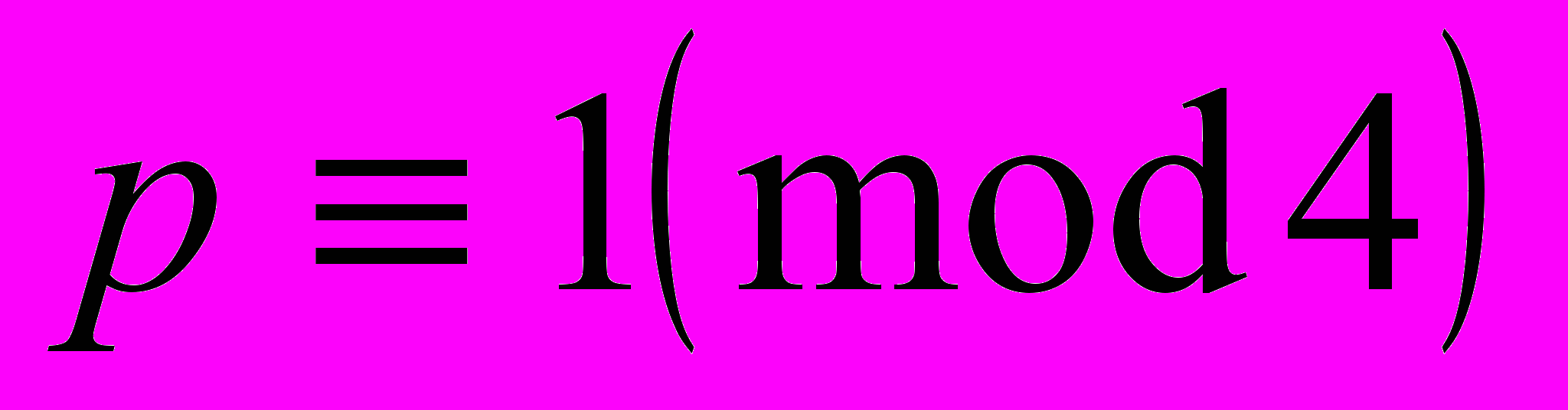в виде суммы двух квадратов

Алгебраические и трансцендентные числа. Теорема Лиувилля и ее применение к построению трансцендентных чисел и к доказательству иррациональности.

2

(2), (3), (4)


2.2. Практические ЗАНЯТИЯ (28 часов)


№
Содержание занятия
часы
Литература и задания

для СР

1
Деление с остатком. Наибольший общий делитель двух целых чисел. Алгоритм Евклида. Линейное представление наибольшего общего делителя чисел a,b в виде d=ax+by. Наименьшее общее кратное.
2
(5), 1, 30-31,

(6), 1-51

2
Простые и составные числа. Признак простого числа. Решето Эратосфена. Разложение натурального числа в произведение простых множителей. Нахождение наибольшего общего делителя (наименьшего общего кратного) целых чисел по их каноническому разложению.
2
(5), 22-29, 36-38

3
Систематические числа.
2
(5) 249-254;

(6), 75-98;

125-162

4
Конечные цепные дроби. Разложение рационального числа в конечную цепную дробь. Подходящие дроби. Таблица подходящих дробей. Погрешность замены рационального числа подходящей дробью.
2
(5), 124-135, 139-151

5
Сравнения по модулю, их основные свойства. Полная и приведенная системы вычетов. Кольцо классов вычетов. Обратимые классы. Нахождение класса вычетов, обратного данному, с помощью подходящих дробей.
2
(5), 97-101, 109-110, 152-159;

(6) 367-388

6
Функция Эйлера. Теоремы Эйлера и Ферма. Нахождение остатка от деления на заданное число.
2
(5), 174-176

7
Сравнения с неизвестной величиной. Класс решений. Равносильные преобразования. Критерий разрешимости и число решений сравнения первой степени. Решение сравнений испытанием элементов полной системы вычетов и методом преобразования коэффициентов.
2
(5) 179-181, 194-198;

(6) 163-208, 253-304

8
Решение сравнений первой степени по формуле Эйлера, с помощью подходящих дробей. Сравнения первой степени и неопределенные уравнения.
2
(5) 184-186, 199-202, 209-211;

(6) 305-330

9
Системы сравнений первой степени. Сравнения по простому модулю. Сравнения по степени простого числа. Редукция сравнения по составному модулю к сравнению по степени простого числа и к сравнениям по простому модулю
2
(5) 246,

(6) 389-391

10
Признаки делимости. Общий признак делимости Паскаля. Признаки делимости на 2, 3, 4, 5, 10к, 7, 11, 13 в десятичной системе счисления. Определение длины периода десятичной дроби.
2
(5) 229-232

11
Порядок (показатель) числа и класса вычетов по данному модулю, его свойства. Число классов с заданным показателем по простому модулю. Нахождение первообразных корней. Индексы чисел и классов по данному простому модулю. Свойства индексов. Построение таблиц индексов. Применение индексов к решению двучленных сравнений 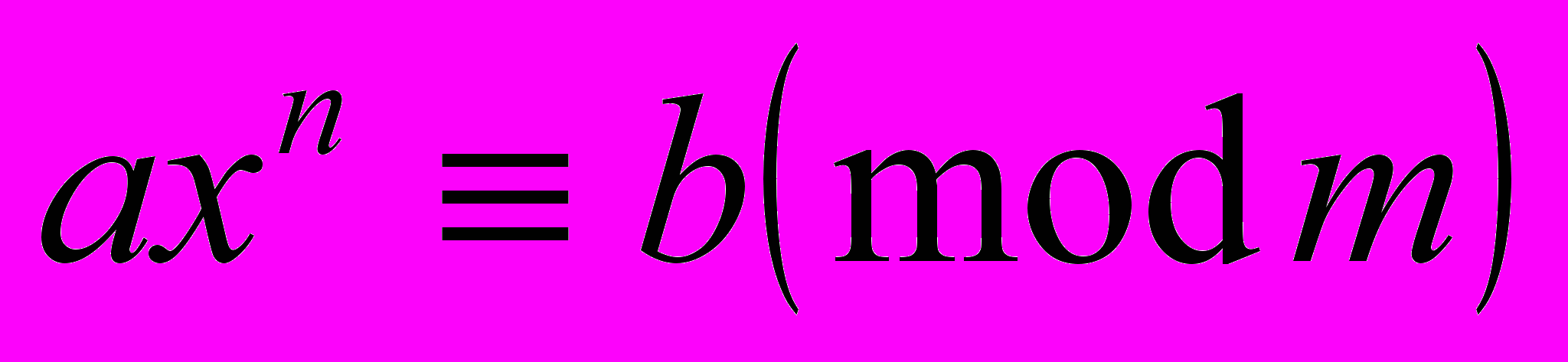и показательных сравнений вида .
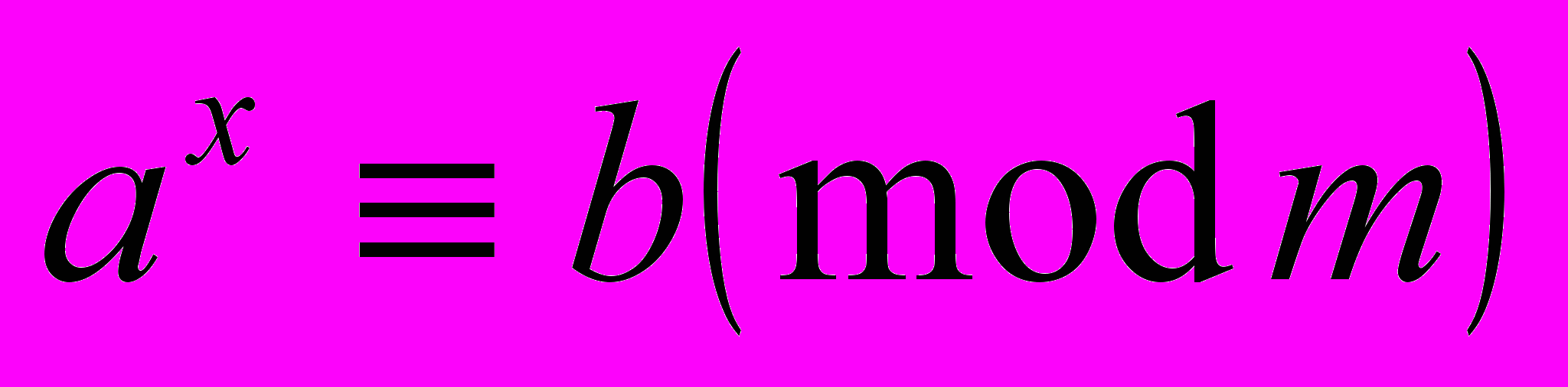2
(5) 234-242

12
Квадратичные вычеты и невычеты. Критерий Эйлера. Символ Лежандра.

2
(5) 212-243

13
Контрольная работа
2



14
Квадратичные иррациональности. Теорема Лагранжа. Алгебраические и трансцендентные числа.
2
(5) 255-260;

264-266;

(6), 99



2.3. САМОСТОЯТЕЛЬНАЯ РАБОТА СТУДЕНТОВ (44 часа)
  1. Подготовка к практическим занятиям, отработка теоретического материала и выполнение домашнего задания. (30 часов)
  2. Подготовка к лекциям. (8 часов)
  3. Подготовка к коллоквиуму: повторение и систематизация изученного материала, решение типовых задач по программе коллоквиума. (6 часов)
  4. Самостоятельное изучение материала, более подробное рассмотрение материала лекций.(10 часов)
  5. Выполнение индивидуального задания.(6 часов)


Рейтинг-контроль.

Точка № 1 - 50% , 11 апреля.

1.Самостоятельныеработы: № 1 ( делимость целых чисел, НОД и НОК, простые и составные числа )

№2 (систематические числа, конечные цепные дроби, подходящие дроби ) – 35%

2. Контрольный опрос по лекциям №1 и №2 – 10%

3. Коллоквиум – 40%

4. Посещаемость занятий, выполнение домашних заданий – 15%

Точка № 2 – 50%, 5 июня.

1. Самостоятельная работа № 3 (сравнения по модулю m, кольцо классов вычетов по модулю m, линейные сравнения с одним неизвестным) – 20%

2. Контрольная работа – 30%

3. Защита индивидуального задания – 25%

4. Теоретический опрос по лекции № 6 – 10%

5. Посещение занятий, выполнение домашних заданий – 15%

Зачёт по конрольным точкам №1 и №2.


4. УЧЕБНО-МЕТОДИЧЕСКАЯ КАРТА

дисциплины ДПП Ф.08 «Теория чисел»


на IV семестр


График аудиторных занятий и самостоятельной работы студентов


Наименование

вида работ
Номер недели

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

Лекции

2
2
2
2
2
2
2
2
2



























Практические занятия

2
2
2
2
2
2
2
2
2
2
2
2
КР
2












Контрольные работы






КО












К












КР















Индивидуальные задания
ВЗ






























ЗЗ