За последние годы в области вычислительной техники произошли существенные изменения
| Вид материала | Лекция |
- А. В. Воронин ПетрГУ, г. Петрозаводск За последние годы в лесопромышленном комплексе, 48.78kb.
- Информатизация образовательного учреждения, 20.47kb.
- «Материаловедение», 378.79kb.
- Закупочная логистика содержание, 151.07kb.
- Тема: «Система складирования в логистической системе», 157.07kb.
- Гильдия Управляющих Документацией, о задача, 36.6kb.
- Общественное мнение о деятельности судебных и правоохранительных органов в Республике, 79.71kb.
- Уважаемые участники семинара, коллеги, 137.99kb.
- Программа дисциплины по кафедре Вычислительной техники микропроцессорные системы, 464.96kb.
- Программа дисциплины по кафедре Вычислительной техники Теория автоматов, 406.16kb.
ВВЕДЕНИЕ
За последние годы в области вычислительной техники произошли существенные изменения. Они были вызваны, прежде всего, тем, что персональные компьютеры превратились из простейших ЭВМ в мощные 64 разрядные вычислительные машины, способные решать самые сложные вычислительные задачи. Во многом такой прогресс в области персональных компьютеров обусловлен успехами микроэлектроники. Уже сейчас количество элементов, расположенных на кристалле микросхемы, перешагнуло рубеж 10 миллионов транзисторов и продолжает увеличиваться. Таким образом, современные СБИС представляют собой сложные функциональные изделия. Наряду с этими схемами продолжается выпуск микросхем малой и средней степени интеграции. В этих условиях требования к подготовке специалистов по вычислительной технике смещаются в область принципов функционирования типовых узлов ЭВМ, технически грамотного применения стандартных микросхем, проектирования полузаказных БИС на основе базовых матричных кристаллов и программируемых логических интегральных схем.
В настоящем учебном пособии рассматриваются основные серии стандартных микросхем, приводятся рекомендации по их применению, методы проектирования и практические схемы функциональных узлов ЭВМ на основе стандартных микросхем, типовые устройства вычислительных машин, реализуемых в виде БИС. По многим микросхемам приведены краткие справочные данные.
ЛЕКЦИЯ 1. ОСНОВЫ АЛГЕБРЫ ЛОГИКИ
Теоретической основой проектирования цифровых систем является алгебра логики или булева алгебра. В булевой алгебре различные логические выражения могут принимать только два значения - “истинно” или “ложно”. Для обозначения истинности или ложности высказываний используют символы “1” или “0”.
В общем случае логические выражения являются функциями логических переменных A, B, C и т. д., каждая из которых может принимать значения “0” или “1”. Если имеется n логических переменных, то они образуют 2n возможных логических наборов из “0” и “1”. При n = 1: A = 0 и A = 1, при n = 2: AB = 00, AB = 01, AB = 10, AB = 11 и т. д. Для каждого набора переменных логическая функция F также может принимать значение “0” или “1”. Тогда для n переменных можно образовать L = 22 различных логических функций. Для n = 2 можно получить L = 16 функций, для n = 3 - L = 256 функций, а для n = 3 - L = 65536 функций. Как следует из приведенного примера, число различных логических функций резко увеличивается с ростом числа переменных.
Все возможные логические функции n переменных можно образовать с помощью трех основных операций: логическое отрицание (инверсия); логическое сложение (дизъюнкция, операция ИЛИ), которая обозначается символами “+”, “\/”; логическое умножение (конъюнкция, логическое И), обозначаемая символами “Ч”, “/\”. Для обозначения эквивалентности логических выражений используется знак равенства “=”. В табл. 1.1...1.3 дано табличное представление логических операций “отрицание”, “сложение” и “умножение”.
| Таблица 1.1 | |
| A | F = 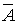 |
| 0 | 1 |
| 1 | 0 |
| Таблица 1.2 | Таблица 1.3 | ||||
| B | A | F =A+B | B | A | F =A B |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 | 0 |
| 1 | 0 | 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 |
Основные законы алгебры логики приведены в табл.1.4
Таблица 1.4. Основные аксиомы и законы алгебры логики
| Аксиомы (тождества) | 1 + A = 1 0 A = 1 |
| 0 + A = A 1 A = A | |
| A + A = A A A = A | |
| A + A = 1 A 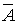 = 0 = 0 | |
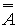 = A = A | |
| Законы коммутативности | A + B = B + A A B = B A |
| Законы ассоциативности | A + B + C = A + (B + C) A B C = A (B C) |
| Законы дистрибутивности | A (B + C) = A B + A C A + (B C) = (A + B) (A + C) |
| Законы дуальности (теоремы де-Моргана) | 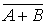 = =  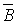 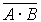 = =  + + 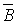 |
| Законы поглощения | A + A B = A A (A+B) = A |
Логические функции могут иметь различные формы представления: словесное, табличное, алгебраическое, графическое. Например для функции равнозначности словесное описание будет выглядеть следующим образом: функция равнозначности истинна тогда, когда А = В и ложна тогда, когда А не равно В.
В табличном виде это будет выглядеть так, как представлено в табл.1.5, а в алгебраической форме: F = А Ч В + A Ч B.
| Таблица 1.5 | ||
| B | A | F |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Для того чтобы совершить переход от табличной формы представления к алгебраической, каждому набору переменных ставится в соответствие минтерм (конституента единицы) - конъюнкция всех переменных в минтерм в прямом виде, если значение данной переменной равно “1” и в инверсном, если значение переменной равно “0”. Для n переменных составляются q = 2n минтермов: m0, m1, ... , mq-1. Функция двух переменных представлена в табл. 1.6.
| Таблица 1.6 | ||||
| A | B | минтермы | макстермы | F |
| 0 | 0 | m0 =  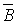 | M0 = A + B | f0 = 1 |
| 0 | 1 | m1 = A 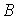 | M1 =  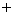 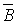 | f1 = 0 |
| 1 | 0 | m2 =  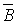 | M2 = 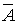 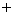 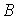 | f2 = 0 |
| 1 | 1 | m3 =  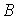 | M3 =  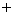 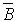 | f3 = 1 |
Как видно из табл.1.5, 1.6 алгебраическое представление функции F является суммой минтермов, соответствующих наборам переменных, для которых
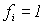 .
.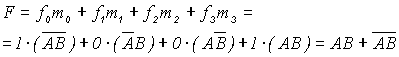 (1.1)
(1.1)В общем случае алгебраическое выражение функции можно представить в следующем виде:
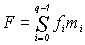 , (1.2)
, (1.2)где
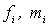 - значение функции (“0” или “1”) и минтерм, соответствующие i-му набору переменных. Такое представление функции называют совершенной дизъюнктивной нормальной формой (СДНФ).
- значение функции (“0” или “1”) и минтерм, соответствующие i-му набору переменных. Такое представление функции называют совершенной дизъюнктивной нормальной формой (СДНФ).Другая алгебраическая форма представления функции, получается при использовании макстермов. Макстермом (конституентой 0) называется дизъюнкция всех переменных, которые входят в прямом виде, если значение переменной равно 0, либо в инверсном виде, если значение переменной равно 1. Число макстермов, как и число минтермов, для функции n переменных равно q = 2n.
Алгебраическое выражение функции получается в виде произведения:
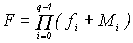 , (1.3)
, (1.3)где
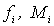 - значение функции и макстерм, соответствующие i-му набору переменных. Такое представление функции называют совершенной конъюнктивной нормальной формой (СКНФ). Например, для функции F получим СКНФ:
- значение функции и макстерм, соответствующие i-му набору переменных. Такое представление функции называют совершенной конъюнктивной нормальной формой (СКНФ). Например, для функции F получим СКНФ: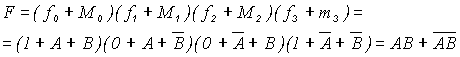 (1.4)
(1.4)Функции, представленные в СДНФ или СКНФ, часто не являются наиболее простыми их выражениями. Используя логические тождества и законы, можно, во многих случаях, получить более простые формы представления функции, которые называются минимизированными.
При относительно небольшом числе переменных (n , 6) весьма удобным и наглядным является графическое представление логической функции в виде так называемых карт минтермов, наиболее распространенной формой которых являются карты Карно. Карта Карно содержит q = 2n клеток, каждая из которых соответствует одному из qi минтермов. Примеры карт Карно для функции двух, трех и четырех переменных представлены на рис.1.1.
| |  |  | | | |  | 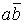 | 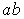 | 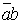 |
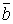 | | | | 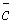 | | | | | |
 | | | | 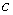 | | | | |
| | 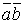 | 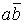 | 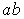 | 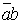 |
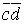 | | | | |
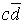 | | | | |
 | | | | |
 | | | | |
Рисунок 1.1 Карты Карно для функции 2-х, 3-х и 4-х переменных.
Для каждого значения функции, равного “1”, в карте на пересечении соответствующих строк и столбцов ставится “1”. Для минимизации логических выражений все клетки, содержащие “1”, объединяются в замкнутые области. Каждая область должна представлять собой прямоугольник с числом клеток 2, 4, 8 и т. д. Области могут пересекаться, и одни и те же клетки могут входить в разные области. Соседними клетками являются не только клетки, расположенные рядом по горизонтали и вертикали, но и клетки, находящиеся на противоположных границах карты.
При охвате клеток замкнутыми областями следует стремиться к минимальному числу областей, каждая из которых содержала бы возможно большее число клеток. Каждый член минимальной дизъюнктивной нормальной формы (МДНФ) составляют лишь из тех переменных, которые для соответствующей области имеют одно значение: без инверсии или с инверсией. Если же переменная для одной клетки области имеет значение без инверсии, а для другой клетки этой же области - с инверсией, то она в соответствующем члене МДНФ не присутствует.
Рассмотрим пример минимизации функции трех переменных, заданной картой Карно (рис.1.2). СДНФ минимизируемой функции описывается выражением (1.5), а МДНФ - выражением (1.6).
| | 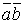 | 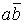 | 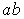 | 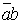 |
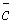 | | | 1 | 1 |
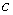 | 1 | | | 1 |
Рисунок 1.2 Пример минимизации функции трех переменных.
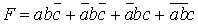 (1.5)
(1.5)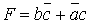 (1.6)
(1.6)Рассмотренные выше логические функции были определены, т. е. имели определенное значение Fi = 0 или Fi = 1 при всех возможных наборах логических переменных. Такие логические функции называются полностью определенными. Кроме них имеется большой класс функций, значение которых определено только для части логических наборов переменных. Такие функции называются частично определенными. Наборы переменных, для которых функция определена, называются рабочими, а для которых не определена - безразличными. Значения функции, соответствующие безразличным наборам, будем обозначать в таблицах истинности и на картах Карно знаком “Х”. Если частично определенная функция представляется в виде СДНФ или СКНФ, то указываются также минтермы (макстермы), соответствующие безразличным наборам.
На практике безразличными являются такие наборы значений логических переменных, которые при работе данного цифрового устройства никогда не реализуются. Частично определенную функцию можно сделать полностью определенной (доопределить), присвоив безразличным наборам какие-либо значения функции: Fi = 0 или 1. Доопределение функции проводится таким образом, чтобы упростить ее алгебраическое выражение, а следовательно и практическую реализацию.
Как уже указывалось выше, любую логическую функцию можно представить в виде СДНФ или СКНФ, т.е. с помощью соответствующей комбинации простейших логических функций “И”, “ИЛИ”, “НЕ”. Набор простейших функций, с помощью которых можно выразить любые, сколь угодно сложные функции - называется функционально полным или логическим базисом.
Логический базис называется минимальным, если удаление хотя бы одной из входящих в него функций превращает этот набор в функционально неполный. Логический базис “И”, “ИЛИ”, “НЕ” не является минимальным, поскольку удаление из него функции “И” либо “ИЛИ” может быть восполнено с помощью законов дуальности. В результате получаем минимальные базисы: “И”, “НЕ” и “ИЛИ”, “НЕ”. Имеются минимизированные логические базисы содержащие только одну функцию: Штрих Шеффера - (И-НЕ), Стрелка Пирса - (ИЛИ-НЕ).
