За последние годы в области вычислительной техники произошли существенные изменения
| Вид материала | Лекция |
- А. В. Воронин ПетрГУ, г. Петрозаводск За последние годы в лесопромышленном комплексе, 48.78kb.
- Информатизация образовательного учреждения, 20.47kb.
- «Материаловедение», 378.79kb.
- Закупочная логистика содержание, 151.07kb.
- Тема: «Система складирования в логистической системе», 157.07kb.
- Гильдия Управляющих Документацией, о задача, 36.6kb.
- Общественное мнение о деятельности судебных и правоохранительных органов в Республике, 79.71kb.
- Уважаемые участники семинара, коллеги, 137.99kb.
- Программа дисциплины по кафедре Вычислительной техники микропроцессорные системы, 464.96kb.
- Программа дисциплины по кафедре Вычислительной техники Теория автоматов, 406.16kb.
В зависимости от технологии изготовления, ИС подразделяются на серии, различающиеся физическими параметрами базовых элементов, а также числом и функциональным назначением входящих в их состав микросхем. В настоящее время наибольшее распространение получили ИС, изготавливаемые по ТТЛ и КМОП технологиям.
В табл. 4.1. представлены основные технические характеристики микросхем ТТЛ- типа.
Таблица 4.1.Основные технические характеристики ТТЛ микросхем
| Обозначение серии (аналог) | tp нс | Pcc мВт | IIH мкА | IIL мА | F МГц | IOH мА | IOL мА | N |
| 155 (SN74) | 10 | 10 | 40 | 1,6 | 10 | 0,4 | 16 | 10 |
| 158 (SN74L) | 33 | 1 | 10 | 0,18 | 3 | 0,2 | 3,6 | 10 |
| 131 (SN74H) | 6 | 22 | 50 | 2 | 33 | 0,5 | 20 | 10 |
| 555 (SN74LS) | 9,5 | 2 | 20 | 0,36 | 30 | 0,4 | 8 | 20 |
| 531 (SN74S) | 3 | 19 | 50 | 2 | 100 | 1 | 20 | 10 |
| 1533 (SN74ALS) | 4 | 1 | 10 | 0,2 | 75 | 0,4 | 8 | 40 |
| 1531 (SN74AS) | 1,5 | 22 | 20 | 0,6 | 130 | 1 | 20 | 33 |
Все серии, указанные в табл. 4.1, совместимы по уровням входных и выходных сигналов. Однако при использовании микросхем из разных серий необходимо учитывать их взаимную нагрузочную способность. Это означает, что к выходу ИС можно подключить столько входов, чтобы их суммарный входной ток не превышал ток нагрузки выхода, т.е. выполнялись условия (4.1) и (4.2).
IOL і N ґ IIL , (4.1)
IOH і N ґ IIH , (4.2)
где IOL, IOH - выходные токи нагрузок, IIL, IIH - входные токи.
В табл. 4.2 приведены основные технические характеристики стандартных КМОП ИС.
Таблица 4.2. Основные технические характеристики КМОП микросхем
| Обозначение серии (аналог) | tp, нс | IOL, мА | Vcc, В |
| 176 (CD4000) | 80 | 0,5 | 9 |
| 561 (CD4000A) | 80 | 0,5 | 3...15 |
| 1561 (CD4000B) | 25 | 1,0 | 3...18 |
| 1564 (MC14000) | 10 | 5,0 | 2...6 |
Микросхемы ЭСЛ типа используются при построении сверхбыстродействующих цифровых устройств и менее распространены, чем ИС ТТЛ или КМОП. Это вызвано прежде всего тем, что они потребляют значительно большую мощность и требуют для своего питания, как правило, двух источников с напряжением -5.2 В (-4.5 В) и -2.2 В. Кроме того, аппаратура, построенная на ЭСЛ микросхемах, обычно проектируется с принудительным воздухообменом (скорость воздушного потока должна быть не менее 2.5 м/с). В табл. 4.3 приведены основные параметры ЭСЛ ИС.
Таблица 4.3. Основные технические характеристики ЭСЛ микросхем
| Обозначение серии (аналог) | tp, нс | Pcc, Вт | Vcc, В |
| 500 (M10K) | 2 | 25 | 5.2 |
| 1500 (M100K) | 0.75 | 40 | 4.5 |
ЛЕКЦИЯ 5. КОМБИНАЦИОННЫЕ УСТРОЙСТВА
Цифровое комбинационное устройство представляет собой функциональный узел, у которого совокупность выходных сигналов в любой момент времени однозначно определяется входными сигналами, поступающими на входы в тот же момент времени. Закон функционирования комбинационных устройств определен, если задано соответствие между его входными и выходными сигналами в любой из возможных форм (алгебраическая, табличная и др.)
5.1 ПРОСТЕЙШИЕ КОМБИНАЦИОННЫЕ УСТРОЙСТВА
К простейшим комбинационным устройствам относятся схемы, реализующие такие логические операции как: И, ИЛИ, ИЛИ-НЕ, И-НЕ, И-ИЛИ-НЕ, Иск. ИЛИ и т.д. На рис. 5.1 показаны условные графические изображения логических элементов (ЛЭ) НЕ, И-НЕ, ИЛИ-НЕ и Искл. ИЛИ, а также их соответствующие изображения, приводящиеся в зарубежной литературе. В табл. 5.1 приведен состав и обозначение ЛЭ, входящих в стандартные ТТЛ серии микросхем.
Таблица 5.1
| Обозначение | Логическая функция | Число входов |
| ЛН1, ЛН2 ЛИ1, ЛИ2 ЛА3, ЛА9, ЛА11, ЛА12, ЛА13 ЛЛ1 ЛЕ1 ЛП5, ЛП12 ЛА1, ЛА6, ЛА7 ЛИ3, ЛИ4 ЛА4, ЛА10 ЛЕ4 ЛП3 ЛА2 | НЕ И И-НЕ ИЛИ ИЛИ-НЕ Искл.ИЛИ И И-НЕ И И-НЕ ИЛИ-НЕ И-НЕ | 1 2 2 2 2 2 4 4 3 3 3 8 |
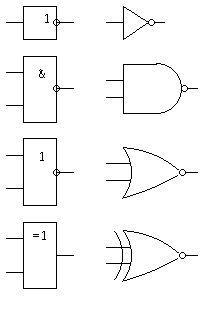
Рисунок 5.1. УГО основных ЛЭ
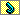
5.2. ДЕШИФРАТОРЫ И ДЕМУЛЬТИПЛЕКСОРЫ
Дешифраторы представляют собой функциональный узел, преобразующий двоичный n - разрядный код в унитарный код “1 из N”. В общем случае дешифратор с n адресными входами имеет 2n выходов. При каждой входной комбинации только один выход Fi принимает значение, равное 1. При этом все остальные выходы находятся в состоянии логического 0 (табл. 5.2). На рис. 5.2 представлена электрическая схема дешифратора 2 х 4, который реализует четыре минтерма двух переменных Х1 и Х2. Если в схеме на рис. 5.2 заменить ЛЭ И на ЛЭ И-НЕ, то получится дешифратор с инверсными выходами. Такие дешифраторы называются полными.
Таблица 5.2. Таблица истинности дешифратора
| x1 | x2 | F1 | F2 | F3 | F4 |
| 0 0 1 1 | 0 1 0 1 | 1 0 0 0 | 0 1 0 0 | 0 0 1 0 | 0 0 0 1 |
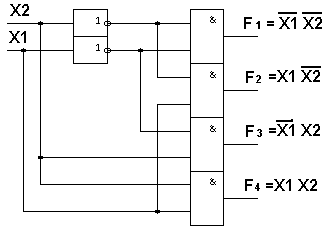
Рисунок 5.2. Схема дешифратора 2 в 4
Если же дешифратор реализует N < 2n минтермов, то он называется неполным. В виде стандартных ИС выпускаются неполные дешифраторы 4 в 10, такие как К155ИД1, К555ИД6 (ИД10) , К561ИД1 и др.
Демультиплексоры представляют собой функциональный узел, коммутирующий управляющий сигнал Е на один из 2n выходов. Электрическая схема демультиплексора показана на рис. 5.3. Он имеет один информационный вход Е, n адресных входов и 2n выходов.
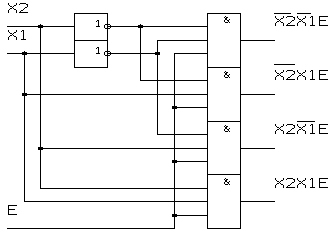
Рисунок 5.3. Схема демультиплексора.
Из сравнения электрических схем дешифратора и демультиплексора видно, что демультиплексор может выполнять функцию дешифратора, если на вход Е подана логическая единица. Если же на вход Е подан низкий уровень, то на всех его выходах также будут низкие уровни независимо от состояния адресных входов. Поэтому вход Е называют еще входом стробирования.
В состав логических серий входят демультиплексоры 1 в 4, 1 в 8, 1 в 16 типа ИД3, ИД4, ИД7, ИД14 и др., которые, как правило, имеют инверсные выходы. Наличие входа Е позволяет строить схемы дешифраторов на значительно большее количество выходов, чем у стандартных демультиплексоров.
В качестве примера рассмотрим электрическую схему дешифратора 4 в 16, построенную на демультиплексорах 1 в 4 (рис. 5.4).
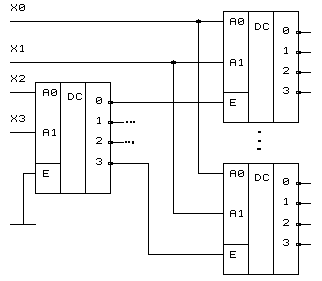
Рисунок 5.4 Схема каскадирования демультиплексоров
На адресные входы демультиплексора первой ступени поданы старшие разряды входного слова Х2, Х3, а адресные входы демультиплексоров второй ступени объединены и на них поступают младшие разряды входного слова Х0, Х1. В зависимости от состояния старших разрядов Х2, Х3 только на одном из выходов демультиплексора первой ступени будет сформирован лог. 0, на остальных же - лог. 1. Эти единицы, поступая на входы стробирования демультиплексоров второй ступени переведут их выходы в единичное состояние и только на одном выходе одного из демультиплексоров, у которого на вход стробирования подан лог. 0, будет присутствовать низкий уровень. Именно таким образом и функционирует дешифратор 4 в 16 с инверсией. Если же на вход Е демультиплексора первой ступени подать управляющий сигнал, то получим демультиплексор 1 в 16.
5.3. МУЛЬТИПЛЕКСОРЫ
Мультиплексором называется функциональный узел, осуществляющий передачу информации с одного из 2n входов (n - число адресных входов) на один выход, т.е. выполняет функцию, обратную демультиплексору. Рассмотрим работу мультиплексора, имеющего два адресных входа S0, S1 и четыре информационных D0... D4 (рис. 5.5)
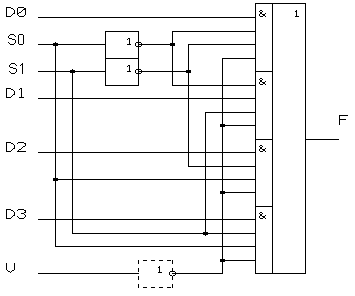
Рисунок 5.5. Схема мультиплексора
В зависимости от состояния входов S0, S1 выбирается один из элементов “И”, т.е. на двух его входах формируется лог.1. В это время на входах остальных элементов “И” присутствует хотя бы один 0. Наличие двух единиц на входах выбранного элемента позволяет передать информацию с информационного входа Di на выход. В мультиплексорах со стробированием каждый элемент И содержит дополнительный вход (пунктирная линия на рис. 5.5). Если на вход V подан высокий уровень, то на 4 в 1 выходе мультиплексора будет низкий уровень независимо от состояния адресных и информационных входов. Управляемая передача информации в таких мультиплексорах будет осуществляться, если на вход V будет подана лог. 0. В состав стандартных серий ИС входит большое количество мультиплексоров, начиная от мультиплексора 2 в 1 (КП11, КП13, КП14, КП16) и заканчивая 16 в 1 (К155КП1), отличающихся друг от друга прямой или инверсной передачей данных, а также схемами выходов (стандартный или с тремя состояниями).
Мультиплексоры на большее число входов приходится строить из мультиплексоров меньшей размерности. Если необходим мультиплексор “N в 1”, а имеются схемы с числом информационных входов N1, то для его реализации потребуется L микросхем в первой ступени, где L = N/N1. Во второй же ступени должен использоваться мультиплексор, у которого число информационных входов должно быть больше L. На рис. 5.6 в качестве примера показана схема построения мультиплексора 16 в 1 на основе ИМС 4 в 1.
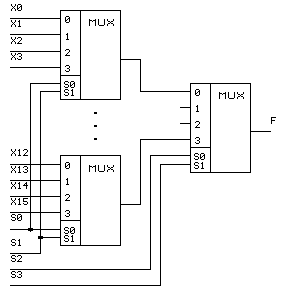
Рисунок 5.6 Схема каскадирования мультиплексоров
Адресные входы мультиплексоров первой ступени объединены и на них подаются младшие разряды адреса S0, S1. Старшие разряды адреса S2, S3 заведены на мультиплексор второй ступени. В зависимости от состояния входов S0, S1 все мультиплексоры первой ступени будут передавать информацию на свои выходы с тех входов данных, которые определены адресным кодом (например, при комбинации S0 = 0, S1 = 1 на выходах мультиплексоров будут присутствовать данные Х2, Х6, Х10, Х14, соответственно). Однако на выход схемы поступят только те данные, которые определены старшей частью адресного кода. Так, если на адресные входы мультиплексора второй ступени подана комбинация S0 = 1, S1 = 1, то на выходе схемы будут присутствовать данные, поступившие на вход Х14 (код входа 1110).
Еще одним из применений мультиплексоров в вычислительной технике является построение на их основе комбинационных сдвигателей. На рис. 5.7 представлен фрагмент электрической схемы сдвигателя вправо на 4 разряда. В табл. 5.3 приведены разряды данных, поступающих на выходы сдвигателя, в зависимости от состояния адресных входов.
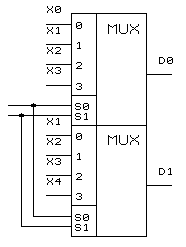
Рисунок 5.7 Фрагмент схемы сдвигателя на мультиплексорах
Таблица 5.3. Таблица функционирования состояния адресных входов.
| S0 | S1 | D0 | D1 |
| 0 | 0 | X0 | X1 |
| 0 | 1 | X1 | X2 |
| 1 | 0 | X2 | X3 |
| 1 | 1 | X3 | X4 |
Важной особенностью рассматриваемых сдвигателей является то, что они могут осуществлять сдвиг сразу на N разрядов, где N - число информационных входов мультиплексора, используемого в комбинационном сдвигателе. Коммутируя соответствующим образом информационные входы мультиплексоров можно строить сдвигатели как вправо, так и влево. Для построения комбинационных сдвигателей была разработана специализированная микросхема К531ИР21, позволяющая сдвигать четырехразрядные данные на 1, 2 или 3 разряда влево или вправо.
Мультиплексор можно использовать в качестве универсального ЛЭ для реализации любой функции от числа аргументов, равного числу адресных входов мультиплексора. Схема, показанная на рис. 5.8, реализует функцию, заданную табл. 5.4. Для этого информационные входы мультиплексора подключены к источникам 0 и 1 в такой последовательности, которая полностью копирует последовательность нулей и единиц в таблице истинности. Однако этот метод реализации логических функций становится весьма громоздким при числе аргументов больше 5.
Таблица 5.4
| S2 | S1 | S0 | F |
| 0 0 0 0 1 1 1 1 | 0 0 1 1 0 0 1 1 | 0 1 0 1 0 1 0 1 | 0 1 1 0 1 0 0 0 |
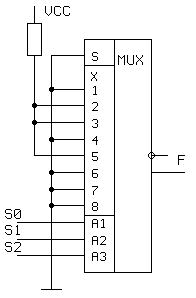
Рисунок 5.8. Реализация заданной функции на мультиплексоре
5.4. ШИФРАТОРЫ
Шифратором называется комбинационная схема, преобразующая код один из N в двоичный код, т.е. выполняющая функцию, обратную дешифратору. При активизации одного из входов шифратора (и только одного входа) на выходах схемы формируется двоичный код, соответствующий номеру активизируемого входа.
Полный двоичный шифратор имеет 2n входов и n выходов. На рис. 5.9 показана электрическая схема шифратора 8 в 3, а в табл.5.5 - его таблица истинности.
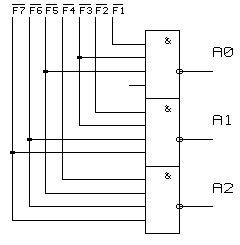
Рисунок 5.9 Схема шифратора 8 в 3
Таблица 5.5
| активный вход | выходы | ||
| A2 | A1 | A0 | |
| F0 F1 F2 F3 F4 F5 F6 F7 | 0 0 0 0 1 1 1 1 | 0 0 1 1 0 0 1 1 | 0 1 0 1 0 1 0 1 |
Из таблицы легко получить выражения, описывающие функционирование выходов шифратора:
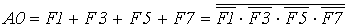, (5.1)
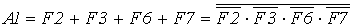, (5.2)
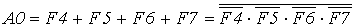. (5.3)На схеме вход F0 никуда не подключен, поскольку сигналу на этом входе соответствует комбинация “все нули”. При этом создается впечатление, что схема не различает ситуаций “подан сигнал на вход F0” или “не подано ни одного сигнала”. Однако это совсем не так, поскольку в определении шифратора присутствует требование об обязательном присутствии сигнала на одном из входов. Одно из основных применений шифратора - ввод данных с клавиатуры.
В устройствах нормализации чисел с плавающей точкой, системах обслуживания приоритетных запросов широкое применение находят схемы выделения старшей единицы. Эти схемы преобразуют n-разрядное слово следующим образом: все старшие нули и самая старшая единица входного кода пропускаются на выход без изменения; все разряды, более младшие, чем старшая единица, заменяются нулями, например: входной код - 001011, выходной код - 001000.
Один из возможных вариантов схемы выделения старшей единицы показан на рис. 5.10. На входы А0, А1, А2 поступает преобразуемое слово (А0 - младший разряд, А2 - старший), на вход EI - входной сигнал разрешения. При EI = 1 схема работает следующим образом. Любое число старших нулей порождает на выходах своих разрядов единицы и никак не влияет на работу более младших элементов И-НЕ. Самая старшая единица генерирует на выходе своего разряда нуль, который поступая на входы более младших элементов И-НЕ устанавливает их выходы в единичное состояние, не зависящее от входной информации. Одновременно на выходе EO (выход разрешения) также установится низкий уровень. Заметим, что на выходах схемы Х0, Х1, Х2 формируются активно низкие уровни.
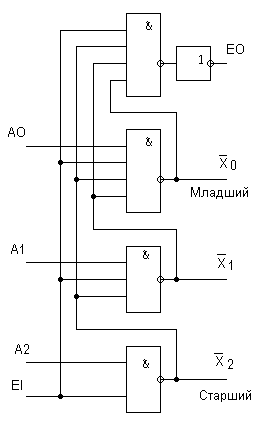
Рисунок 5.10 Схема выделения старшей единицы
Если разрядность обрабатываемого слова превышает разрядность схемы, то используется каскадирование схем, при котором выход EO более старшей схемы соединяется со входом EI более младшей схемы. При таком способе наращивания разрядности любая самая старшая единица, поступившая на вход старшей схемы, установит в неактивное единичное состояние не только свои более младшие разряды, но по цепочке EO-EI и выходы младших схем.
Если к выходу схемы выделения старшей единицы подключить шифратор, то в сумме получится функциональный узел, называемый приоритетным шифратором, формирующий в двоичном коде номер самой старшей единицы из всех присутствующих во входном слове.
На рис. 5.11 показана схема восьмивходового приоритетного шифратора.
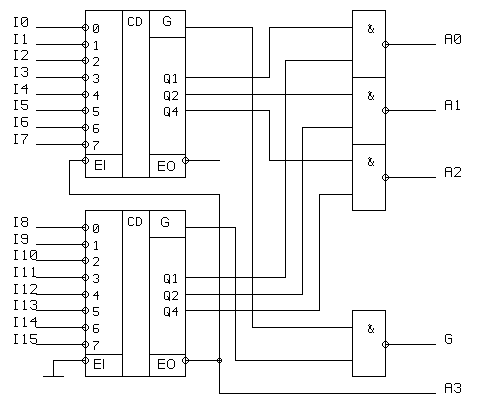
Рисунок 5.11. Схема 8-входового приоритетного шифратора
Собственно приоритетный шифратор построен в соответствии с принципами, изложенными выше. Новым здесь является тракт групповых переносов, к которым относятся вход EI и два выхода EO и G. Вход EI активно низкий. Если на него подана логическая 1, то на всех выходах шифратора устанавливаются высокие уровни. Это свидетельствует о том, что входы приоритета I0 - I7 - блокированы. Сигнал на выходе G (G = 0) свидетельствует о наличии хотя бы одного возбужденного входа Ii при включенном состоянии шифратора. Низкий уровень напряжения на выходе EO говорит о том, что на все входы приоритета поданы неактивные высокие уровни напряжения. Таким образом, его можно использовать для каскадирования приоритетных шифраторов. На рис. 5.12 показана схема приоритетного шифратора 16 в 4, построенного на микросхемах типа К155ИВ1. Наивысший приоритет имеет вход I15. Верхний шифратор включается только в том случае, если не возбужден ни один из входов приоритета нижнего шифратора. Логические элементы 2И-НЕ выполняют функцию “ИЛИ” в отрицательной логике для выходных сигналов А0 - А3, G двух шифраторов.
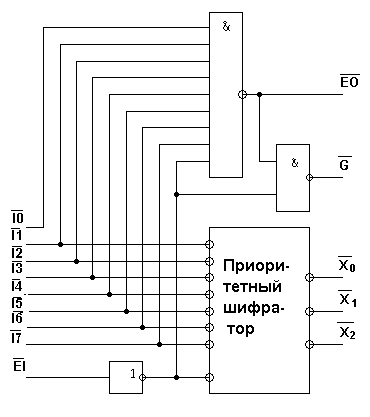
Рисунок 5.12 Каскадирование приоритетных шифраторов
В состав практически всех серий микросхем входят приоритетные шифраторы, различающиеся типом выхода и возможностью наращивания. Так, например, в серию 555 входит 3 приоритетных шифратора ИВ1 - 8 в 3, ИВ2 - 8 в 3, выходы которого имеют три состояния, ИВ3 - 10 в 4 (без наращивания).
Для правильного функционирования многоразрядных схем сравнения на дополнительные входы младшей микросхемы A>B и A
Логические компараторы широко используются в устройствах автоматики для сигнализации о выходе контролируемых величин за пределы допуска, в приводах следящих систем для определения направления воздействия, а также в устройствах контроля и диагностики ЭВМ.
5.5. ЛОГИЧЕСКИЕ КОМПАРАТОРЫ
Логическим компаратором называется функциональный узел, позволяющий определить отношение между двумя двоичными числами. Основным отношением можно считать отношение типа равно, обозначающееся Fа = b и отношение больше Fа >b.
Остальные отношения можно получить из основных. Например: функцию неравенства Fа-b можно получить отрицанием Fа = b, а функцию “меньше” можно получить из функции “больше” путем перестановки аргументов Fа >b = Fb < а. Нестрогие неравенства получаются согласно выражениям:
Fа
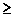b= Fа= b + Fа > b, (5.4)Fа
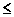b = Fа= b + Fа < b. (5.5)Устройства сравнения на равенство строятся на основе поразрядных операций над одноименными разрядами сравниваемых слов. Признак равенства Ri- го разряда будет равен единице в том случае, если в сравниваемых разрядах содержатся либо 0, либо единицы, т.е.
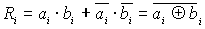(5.6)Поскольку выражение (5.6) содержит как прямые, так и инверсные значения переменных, то преобразуем его к виду:
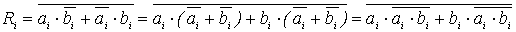(5.7)Полученное соотношение приводит к схеме на рис. 5.13, где входные переменные присутствуют только в прямом виде.
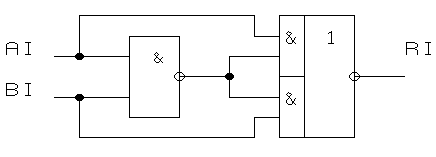
Рисунок 5.13 Один разряд схемы сравнения.
Для сравнения многоразрядных слов выходы полученной схемы объединяются логическим И. Функция сравнения на “больше”, “меньше” для одноразрядных слов определяется табл. 5.6. Из таблицы видно, что
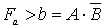.Таблица 5.6
| A | B | Ri | Fа > b |
| 0 0 1 1 | 0 1 0 1 | 1 0 0 1 | 0 0 1 0 |
Для двухразрядных чисел функцию Fа > b можно получить из следующих рассуждений. Если в старшем разряде слова A единица, а в слове B - 0, то независимо от младших разрядов А > В и функция Fа > b = 1. Если же старшие разряды идентичны, то следует анализировать информацию в младших разрядах по тем же правилам, что и для старших разрядов. Тогда выражение для функции Fа > b можно записать в виде:
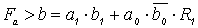, (5.8) где
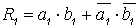- признак равенства второго разряда.Рассуждая аналогичным образом, можно получить выражение для сравнения n - разрядных слов:
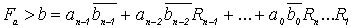(5.9)В соответствии с 5.9 можно реализовать схему сравнения двух n-разрядных слов, с формированием признаков Fа > b и Fа = b. Однако, как следует из приведенного выражения, количество аргументов последнего члена выражения 5.9 для функции Fа > b быстро растет с увеличением разрядности сравниваемых операндов. Поэтому на практике разрядность сравниваемых чисел на одной микросхеме ограничивается четырьмя разрядами. А для сравнения чисел большей разрядности в эти микросхемы вводятся три дополнительных входа: A>B, A=B, A
5.6. СХЕМЫ КОНТРОЛЯ ЧЕТНОСТИ И НЕЧЕТНОСТИ
Схемы контроля четности или нечетности предназначены для контроля передачи данных в информационных каналах. В основе их лежит принцип подсчета единиц в передаваемом слове. Причем, заранее оговаривается условие контроля. Например: в 9-ти разрядном слове количество единиц четное.
При этом 8 разрядов несут информацию о действительном значении числа или его части, а 9-ый разряд формируется специальной схемой так, чтобы количество единиц было четным. На приемном конце устанавливается схема, подсчитывающая количество единиц в переданном слове и вырабатывающая признак четности или нечетности. В качестве такой схемы чаще всего используют пирамидальную схему свертки по модулю 2 (рис.5.15).
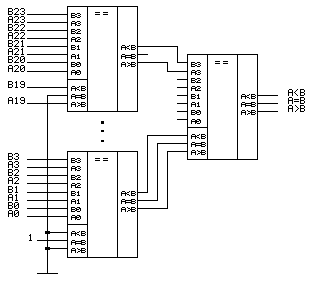
Рисунок 5.14. Фрагмент схемы сравнения 24-х разрядных чисел.
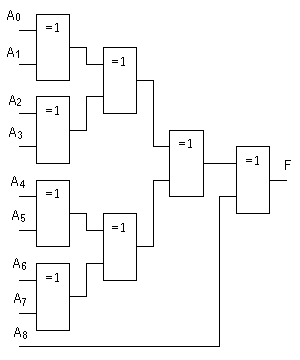
Рис. 5.15. Схема свертки по модулю 2
В стандартные серии ИС входят 9-ти разрядные схемы контроля четности (нечетности) типа ИП5, имеющие два выхода - четности и нечетности. Каскадирование этих микросхем также осуществляется по пирамидальной схеме.
5.7. СХЕМЫ АРИФМЕТИЧЕСКИХ УСТРОЙСТВ
Схемы арифметических устройств являются неотъемлемой частью любой ЭВМ. До последнего времени эти устройства строились на основе дискретных элементов, таких как полные одноразрядные сумматоры, арифметико-логические устройства и матричные умножители. Однако в современных средствах вычислительной техники арифметические операции реализуются, в основном, на микропроцессорах, в состав которых входят указанные блоки. В связи с этим работу и принципы построения арифметических устройств будем рассматривать в минимальном объеме с точки зрения функционирования в составе микропроцессорных средств.
Простейшим арифметическим устройством является полный одноразрядный сумматор, который выполняет арифметическое сложение двух двоичных чисел Ai и Bi и входного переноса Ci, образуя на выходе сигналы суммы Si и выходного переноса Ci+1. Таблица истинности полного одноразрядного сумматора приведена в табл. 5.7, а один из вариантов его схемы на рис. 5.16.
Таблица 5.7
| Ai | Bi | Ci | Si | Ci+1 |
| 0 0 0 0 1 1 1 1 | 0 0 1 1 0 0 1 1 | 0 1 0 1 0 1 0 1 | 0 1 1 0 1 0 0 1 | 0 0 0 1 0 1 1 1 |
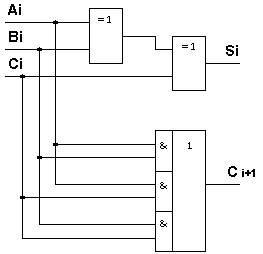
Рисунок 5.16 Схема полного одноразрядного сумматора
Из табл. 5.7 легко получить логические выражения для сигналов Si и Ci+1:
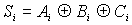, (5.10)
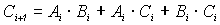. (5.11)В состав ряда стандартных серий ИС входят микросхемы полных одноразрядных сумматоров типа ИМ1, ИМ2, ИМ3, содержащих в одном корпусе от одного до четырех сумматоров.
Одноразрядные сумматоры являются основой для построения многоразрядных сумматоров. В зависимости от способа организации переноса между разрядами различают сумматоры с последовательным, параллельным , групповым, параллельно-параллельным переносом и т.д.
Наиболее простой структурой обладают многоразрядные сумматоры с последовательным переносом, электрическая схема которого показана на рис. 5.17, а. Вычитание в цифровых системах выполняется суммированием чисел в обратном или дополнительном коде. Поэтому в арифметических устройствах обычно используются универсальные сумматоры - вычитатели, выполняющие обе эти операции.
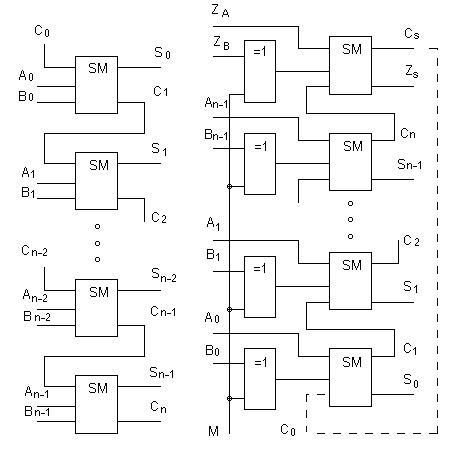
| а) | б) |
Рисунок 5.17 Структура n-разрядного сумматора (а) и сумматора-вычитателя (б)
При вычитании с использованием дополнительного кода структура сумматора-вычитателя имеет вид, показанный на рис. 5.17, б. Включенный на входе сумматора преобразователь в обратный код, реализованный на элементах Искл. ИЛИ, при выполнении вычитания (М = 1) инвертирует число В, а при сложении пропускает его на вход сумматора без изменения. При вычитании с использованием обратного кода числа А и В поступают на вход сумматора в обратном коде, если они отрицательны, и в прямом, если положительны. В таком же коде образуется и результат операции S. При этом для получения правильного результата вводится цепь циклического переноса (штриховая линия на рис. 5.17, б).
Сигналы переноса распространяются в схеме последовательно от сумматора к сумматору и определяют время формирования суммы ts, которое можно оценить по формуле
ts = tpa + (n-2)tpc + tps, (5.12)
где tpa - время задержки распространения сигнала от входов сумматора до выхода переноса;
tps, tpc - время задержки распространения сигнала от входа переноса до выходов суммы и переноса, соответственно; n - разрядность сумматора.
Основным недостатком сумматоров с последовательным переносом является их низкое быстродействие. С целью повышения быстродействия многоразрядных сумматоров в них обычно используются, так называемые, ускоренные методы формирования переноса. Если обозначить через Pi = Ai + Bi и Gi = AiЧBi, то легко видеть, что сигнал Ci+1 в соответствии с выражением (5.11) может быть записан в виде:
Ci+1 = Gi + Pi Ч Ci . (5.13)
Сигналы переноса в каждом разряде формируются одновременно в соответствии с выражениями:
C1 = G0 + P0 Ч C0
C2 = G1 + P1 Ч C1 = G1 + P1 Ч G0 + P1 Ч P0 Ч C0.
В обобщенном виде получим:
Ci+1 = Gi + PiGi-1 + PiPi-1Gi-2 +...+ PiPi-1...P1P0C0. (5.14)
Как видно из выражения (5.14), сложность функции и соответственно схем формирования переноса Ci+1 быстро возрастает при увеличении i. Поэтому на практике разрядность таких схем, получивших название схем ускоренного переноса, не превышает четырех. Функция Si образуется в соответствии с выражением (5.10) в следующей форме:
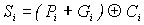.В соответствии с изложенными принципами построены стандартные микросхемы четырехразрядных сумматоров с ускоренным переносом типа ИМ6, входящие в состав многих серий ИС. Кроме того, в виде отдельных ИС выпускаются схемы ускоренного переноса (ИП4).
Эти микросхемы предназначены для построения многоразрядных сумматоров (n = 8, 12, 16, ...), у которых разряды объединены в группы, обычно по четыре разряда. Формирование же переносов между группами осуществляет схема ускоренного переноса. На рис. 5.18 показана структура 16-разрядного сумматора, построенного на микросхемах четырехразрядных сумматоров и схеме ускоренного переноса.
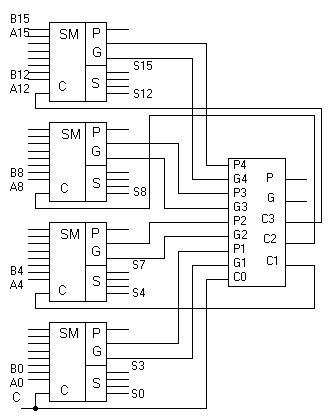
Рисунок 5.18 Структура 16-разрядного сумматора с ускоренным переносом.
Для организации ускоренного переноса между группами из четырех разрядов используются два вспомогательных сигнала - CRP и CRG (групповые сигналы распространения переноса и генерации переноса), формируемые в соответствии с выражениями:
,
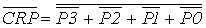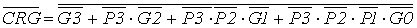.В процессе обработки информации в ЭВМ возникает необходимость выполнения как арифметических, так и логических операций над двумя операндами. Эта задача решается с использованием арифметико-логических устройств (АЛУ). Обычно АЛУ выполняют некоторый набор логических и арифметических операций, причем число логических операций обычно равно числу арифметических операций.
Выпускаемое в виде стандартной ИС АЛУ типа ИП3 позволяет выполнять 16 логических и 16 арифметических операций над двумя 4-х разрядными операндами. Условное графическое изображение АЛУ на электрических схемах показано на рис. 5.18.
АЛУ имеет по четыре входа данных (А0...А3 и В0...В3), вход переноса (CRN) и пять входов управления (М0 и SED0...SED3).
Сигнал на входе М0 определяет арифметические или логические операции будет выполнять АЛУ, а сигналы на входах SED0...SED3 - тип операции. Для каскадирования схем АЛУ в ней предусмотрены выходы последовательного переноса (CRN+4) и групповых переносов (CRP и CRG), которое осуществляется точно также, как и при наращивании разрядности сумматоров. При построении АЛУ с разрядностью более 16 бит используется еще один дополнительный ярус схем ускоренного переноса.
Умножение является одной из наиболее распространенных операций, выполняемых в современных цифровых системах. Традиционным для ЭВМ является способ перемножения чисел путем последовательного выполнения операций сложения и сдвига в течение n машинных тактов, где n - разрядность операндов. Однако время умножения при этом оказывается весьма значительным, что является недопустимым для ряда приложений. Поэтому были разработаны различные варианты быстродействующих “однотактных” умножителей, получивших название матричных умножителей.
Структура матричных умножителей тесно связана со структурой математических выражений, описывающих эту операцию. В качестве примера рассмотрим схему перемножения двух целых двоичных чисел:
| | | | x | a3 | a2 | a1 | a0 |
| | | | b3 | b2 | b1 | b0 | |
| | | + | | a3 b0 | a2 b0 | a1 b0 | a0 b0 |
| | | a3 b1 | a2 b1 | a1 b1 | a0 b1 | | |
| | | a3 b2 | a2 b2 | a1 b2 | a0 b2 | | |
| | a3 b3 | a2 b3 | a1 b3 | a0 b3 | | | |
| P7 | P6 | P5 | P4 | P3 | P2 | P1 | P0 |
Члены вида aibj, где i = 0, m-1 и j = 0, n-1, легко могут быть получены с помощью двухвходовой схемы И. Сложение же частичных произведений легко осуществить на матрице полных одноразрядных сумматоров (рис. 5.20).
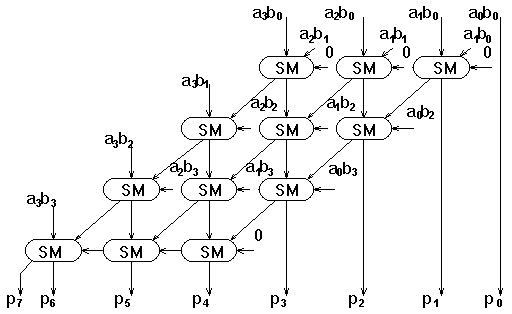
Рисунок 5.20 Структура матричного умножителя
В настоящее время разработано значительное количество структур матричных умножителей, отличающихся друг от друга способами организации цепей переноса, подачи частичных произведений и их формированием, организацией матрицы сумматоров и т.д. Эти функциональные блоки выпускаются как в виде отдельных СИС и БИС, так и входят в состав микропроцессоров в виде операционных блоков. Среди стандартных микросхем выделим следующие ИС: К564ИП5 - умножитель 2х2, К555ИП8 - 4х2, К531ИК1 - 4х2. В состав микропроцессорного комплекта серии 1802 входят 3 БИС матричных умножителей: ВР3 - 8х8, ВР4 - 12х12, ВР5 - 16х16 разрядов.