Методическое пособие для абитуриентов по специальности 080505 управление персоналом
| Вид материала | Методическое пособие |
- Учебно-методическое пособие по курсу «социальная психология» для студентов специальности, 835.23kb.
- Одобрено учебно-методическим советом факультета управления Управление организацией, 2001.44kb.
- Учебно-методический комплекс Для специальностей: 080505 Управление персоналом Москва, 466.07kb.
- Учебно-методический комплекс Для специальности 080505 Управление персоналом, 427.67kb.
- Министерство образования и науки российской федерации, 1182.35kb.
- Учебно-методический комплекс Для специальности 080505 Управление персоналом Москва, 1405.6kb.
- Программа междисциплинарного экзамена по специальности 080505 «Управление персоналом», 251.94kb.
- Учебно-методический комплекс Для специальности 080505 Управление персоналом, 813.21kb.
- Программа вступительного собеседования для специальности 080505 «Управление персоналом», 83.73kb.
- Учебно-методический комплекс Специальность: 080505 Управление персоналом Москва 2009, 1080.32kb.
Геометрия
- Прямая. Луч. Отрезок. Ломаная. Длина отрезка. Угол. Величина угла. Вертикальные и смежные углы.
- Окружность и круг. Центр, радиус, хорда, диаметр. Касательная к окружности, секущая. Дуга окружности. Круговой сектор. Центральные и вписанные углы. Длина окружности, длина дуги окружности. Радианная мера угла.
- Многоугольник. Вершины, стороны, диагонали. Правильный многоугольник.
- Треугольник, его медиана, биссектриса, высота. Виды треугольников. Соотношения между сторонами и углами прямоугольного треугольника.
- Четырехугольники: параллелограмм, прямоугольник, ромб, квадрат, трапеция.
- Площадь треугольника, прямоугольника, параллелограмма, ромба, квадрата, трапеции.
- Площадь круга, площадь сектора.
- Равенство и подобие фигур. Отношение площадей подобных фигур. Симметрия.
- Вписанные и описанные фигуры на плоскости.
- Прямые в пространстве. Параллельность и перпендикулярность прямых. Скрещивающиеся прямые. Угол между прямыми.
- Прямая и плоскость в пространстве. Параллельность и перпендикулярность прямой и плоскости. Угол между прямой и плоскостью. Перпендикуляр к плоскости.
- Плоскости в пространстве. Двугранные углы. Линейный угол двугранного угла. Параллельность и перпендикулярность двух плоскостей.
- Многогранник. Вершины, ребра, грани, диагонали. Прямая и наклонная призмы, пирамиды. Правильная призма и правильная пирамида. Параллелепипеды.
- Фигуры вращения: цилиндр, конус, сфера, шар. Центр, радиус, диаметр сферы и шара. Плоскость, касательная к сфере.
- Вписанные и описанные фигуры в пространстве. Сечение фигуры плоскостью.
- Площадь поверхности и объем призмы, пирамиды, цилиндра, конуса, шара.
- Координатная прямая. Числовые промежутки. Декартовы координаты на плоскости и в пространстве. Векторы. Операции над векторами.
Требования к абитуриенту
На письменном экзамене по математике поступающий должен оформлять решение логически правильно, последовательно и полно, с необходимыми пояснениями. Он должен уметь:
- выполнять (без калькулятора) действия над числами и числовыми выражениями;
- сравнивать числа и находить их приближенные значения (без калькулятора);
- переводить одни единицы измерения величин в другие;
- преобразовывать буквенные выражения;
- доказывать тождества и неравенства;
- решать уравнения, неравенства, системы уравнений и системы неравенств;
- исследовать функции, строить графики функций;
- выполнять действия над векторами (сложение, умножение на число, скалярное произведение);
- пользоваться свойствами чисел, векторов, функций и их графиков, свойствами арифметической и геометрической прогрессий;
- изображать геометрические фигуры на чертеже; строить сечения; исследовать взаимное расположение фигур; применять признаки равенства и подобия фигур;
- пользоваться свойствами геометрических фигур, их характерных точек, линий, частей, свойствами равенства, подобия и взаимного расположения фигур;
- пользоваться соотношениями и формулами, содержащими модули, степени, корни, логарифмические, тригонометрические выражения, величины углов, длины, площади, объемы;
- составлять уравнения, неравенства и системы уравнений и неравенств для нахождения значения величин, исходя из условия задачи.
Содержание тестовых заданий
1 уровень
1. Нахождение значения выражения, содержащего иррациональности, степени с рациональным показателем.
2. Область определения функции. Множество значений функции.
3. Свойства функции и графики функции.
4. Решение неравенства методом интервалов.
5. Преобразование иррациональных, степенных, логарифмических и тригонометрических выражений.
6. Производная функции: таблица производных, правила дифференцирования.
2 уровень
7. Уравнение с модулем.
8. Решение иррациональных, показательных, логарифмических, тригонометрических уравнений.
9. Решение иррациональных, показательных, логарифмических, тригонометрических неравенств.
10. Производная функции: геометрический смысл, физический смысл.
11.Текстовая задача на проценты, движение, работу.
3 уровень
12. Задача на нахождение наибольшего и наименьшего значений функции. Задача на нахождение экстремального значения функции с помощью производной.
13. Задача по планиметрии. Задача по стереометрии.
14. Задачи с параметром.
Демонстрационный вариант тестовых заданий
| № | Текст задания | Варианты ответов |
| 1 уровень | ||
| К каждой задаче первого уровня предложены 4 варианта ответа, один из которых является правильным. Задачи считаются решенными, если выбран правильный ответ. | ||
| 1 | Упростите выражение:  . . | А)  ; ;Б)  ; ;В) 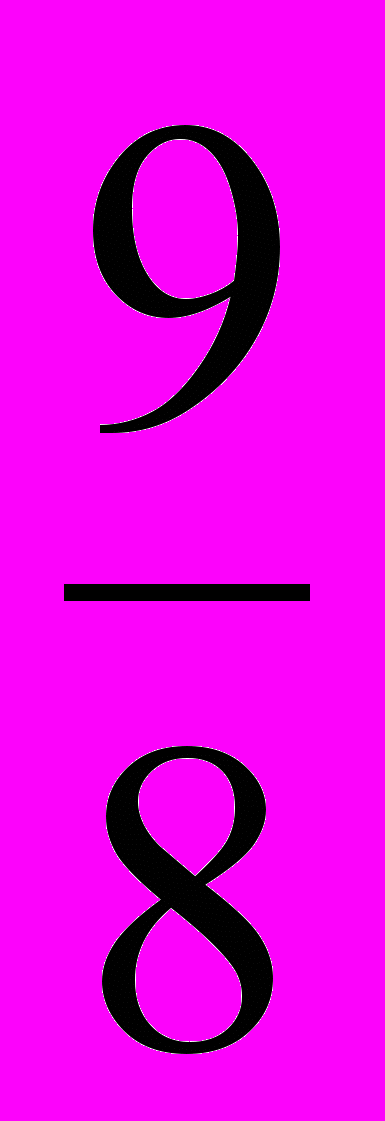 ; ;Г)  . . |
| 2 | Укажите наибольшее значение функции:  . . | А) 11; Б) –5; В) 1; Г) 6. |
| 3 | Укажите область определения функции:  . . | А)  ; ;Б)  ; ;В)  ; ;Г)  . . |
| 4 | Решите неравенство:  . . | А) 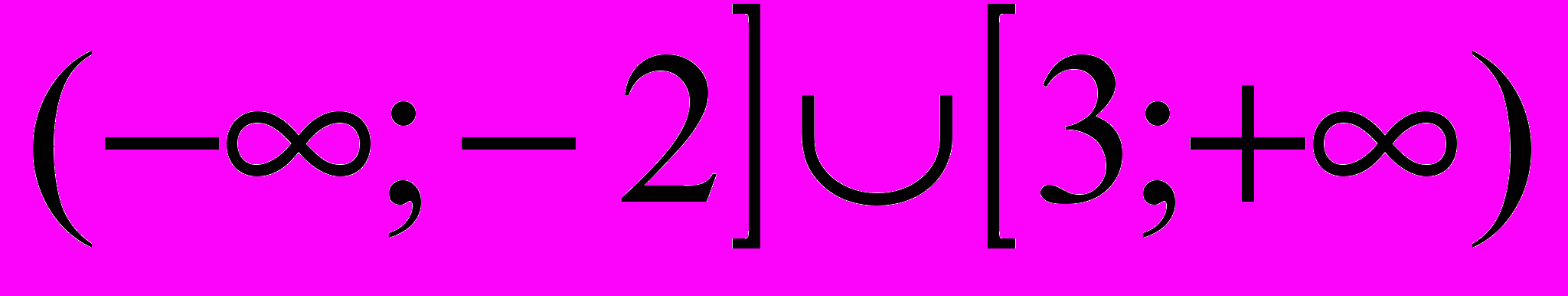 ; ;Б) 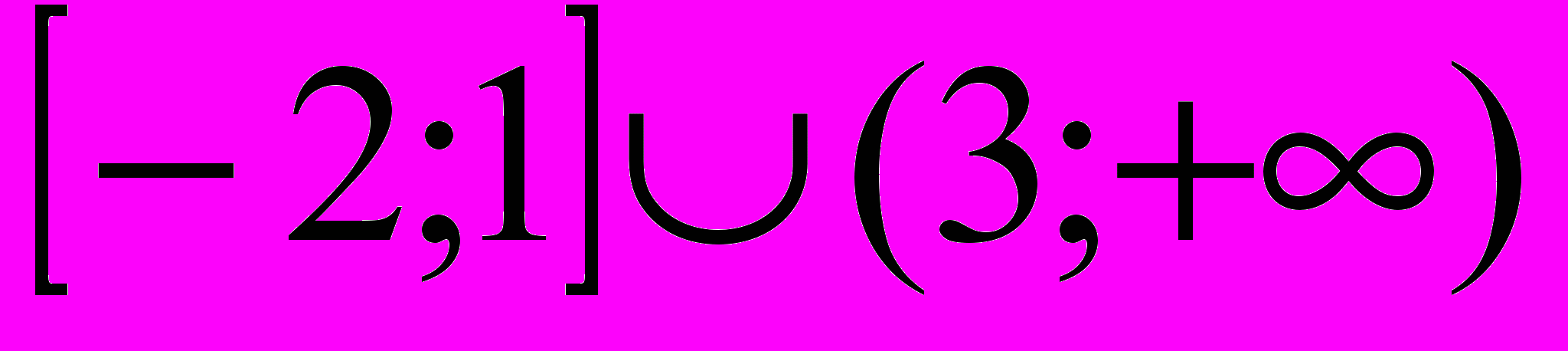 ; ;В) 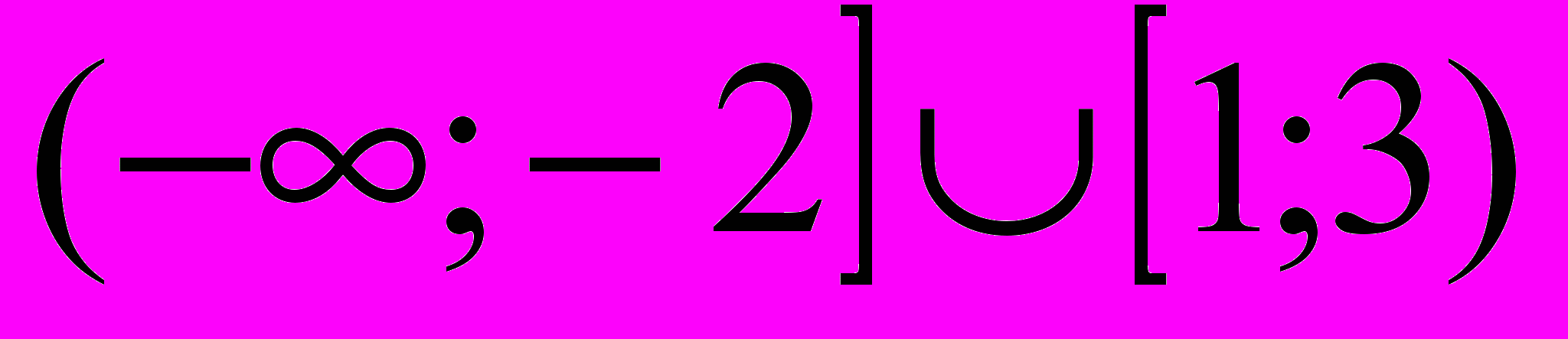 ; ;Г)  . . |
| 5 | Найдите значение выражения 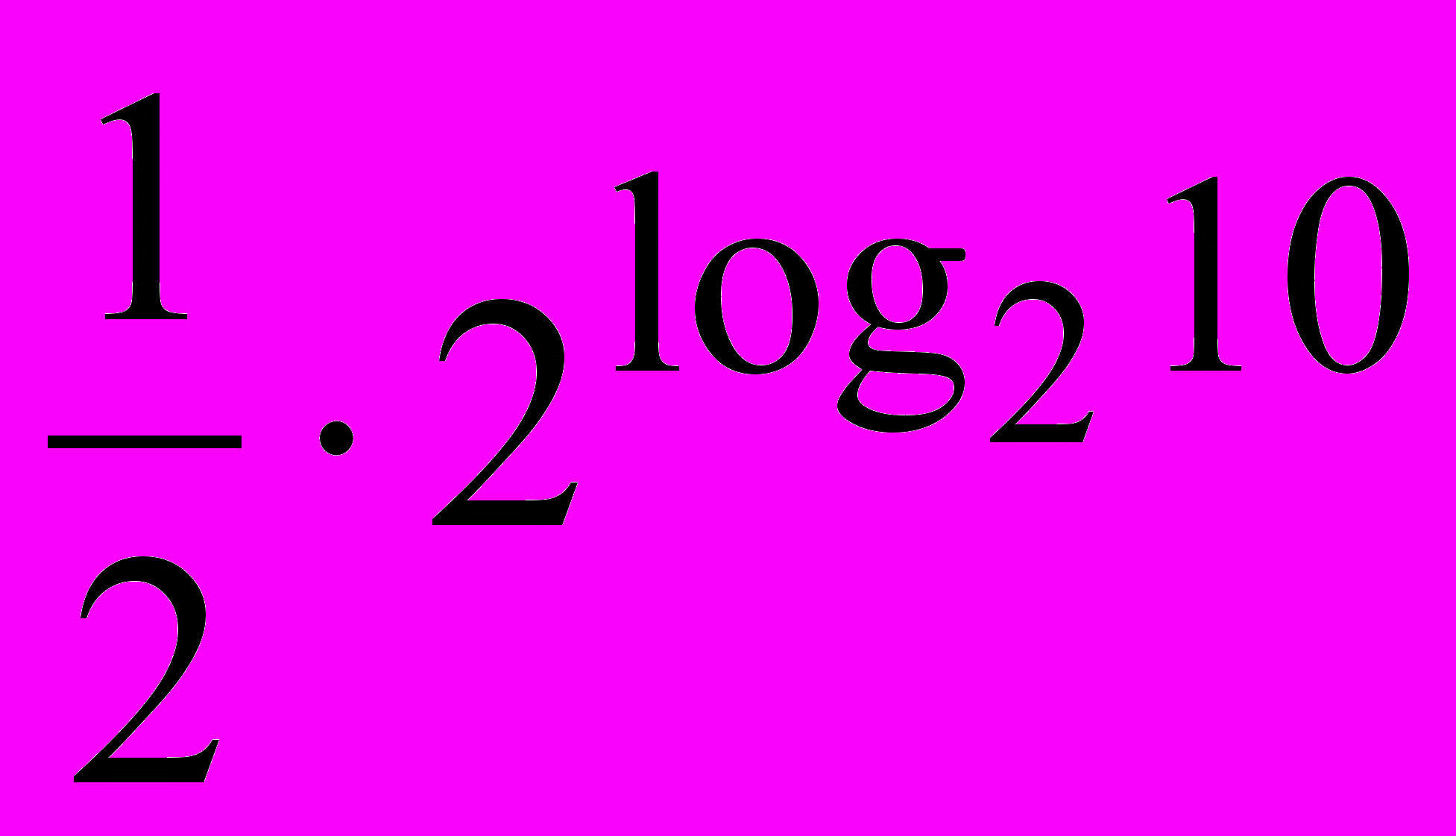 | А) 10; Б) 5; В)  ; ;Г) 20. |
| 6 | Найдите производную функции:  . . | А)  ; ;Б)  ; ;В)  ; ;Г)  . . |
| 2 уровень | ||
| При решении задач второго уровня решением является число. Задача считается решенной, если дан правильный числовой ответ. | ||
| 7 | Найдите наименьший корень уравнения  . . | |
| 8 | Решите уравнение:  | |
| 9 | Найдите наименьшее целое решение неравенства:  . . | |
| 10 | Найдите абсциссу точки графика функции  , в которой угловой коэффициент касательной равен 0. , в которой угловой коэффициент касательной равен 0. | |
| 11 | По пенсионному вкладу банк выплачивает 10% годовых. По истечении каждого года начисляются проценты, и начисленная сумма добавляется к вкладу. Клиент открыл счет на 50000 рублей, который не пополнял и не снимал с него деньги в течение 3 лет. Какой доход был получен по истечении этого срока? | |
| 3 уровень | ||
| При решении задач 3 уровня необходимо привести развернутую запись решения. Задача считается решенной, если приведена развернутая запись решения с обоснованием каждого этапа и получен правильный ответ. | ||
| 12 | Найти количество точек экстремумов функции  . . | |
| 13 | Стороны основания прямого параллелепипеда равны 1 см и 3 см, а синус угла между ними равен  . Найдите угол, который образует большая диагональ параллелепипеда с основанием, если боковое ребро параллелепипеда равно . Найдите угол, который образует большая диагональ параллелепипеда с основанием, если боковое ребро параллелепипеда равно 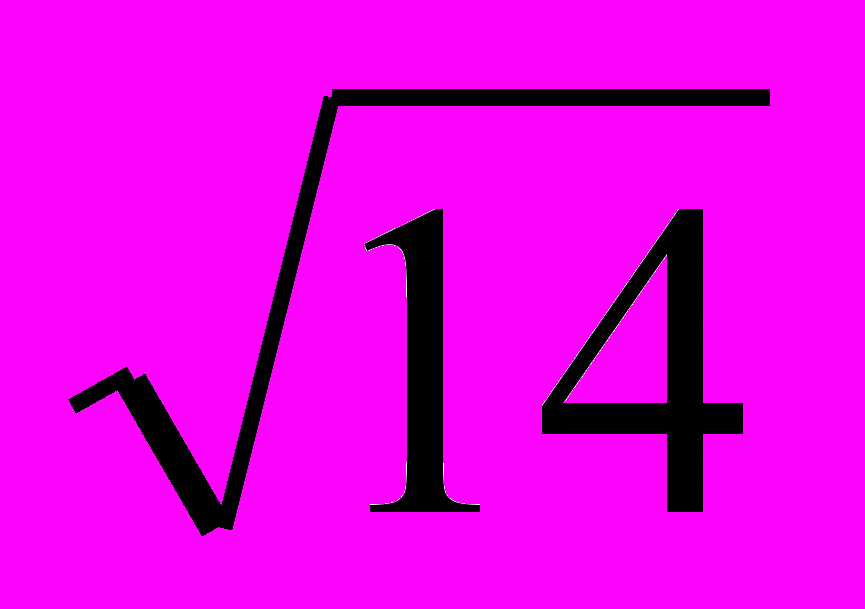 см. см. | |
| 14 | При каком b отношение корней уравнения  равно 5? равно 5? | |
Ответы к заданиям демонстрационного варианта
| № задания | Ответ |
| 1 | А |
| 2 | В |
| 3 | Г |
| 4 | В |
| 5 | Б |
| 6 | В |
| 7 | –8 |
| 8 | 6 |
| 9 | 1 |
| 10 | 2 |
| 11 | 16550 |
| 12 | 1 |
| 13 |  |
| 14 | |
Критерии выставления баллов за тестовые задания:
| Уровень | № заданий | Количество баллов |
| 1 | 1–6 | 4 |
| 2 | 7–11 | 8 |
| 3 | 12–14 | 12 |
