Програми для загальноосвітніх навчальних закладів Математика
| Вид материала | Документы |
- Атики в 5-9 класах загальноосвітніх навчальних закладів вивчатиметься за програмами,, 164.05kb.
- Особливості навчальної програми для учнів 8 класу загальноосвітніх навчальних закладів, 602.24kb.
- «Математика в школі», 894.13kb.
- «Математика в школі», 804.81kb.
- Програма для загальноосвітніх навчальних закладів (класів) з поглибленим вивченням, 717.77kb.
- Програми та рекомендації до розподілу програмного матеріалу загальноосвітніх навчальних, 2950.56kb.
- Програми та рекомендації до розподілу програмного матеріалу загальноосвітніх навчальних, 2719.13kb.
- Програми та рекомендації до розподілу програмного матеріалу загальноосвітніх навчальних, 1209.62kb.
- Програми та рекомендації до розподілу програмного матеріалу загальноосвітніх навчальних, 2778.79kb.
- Методичні рекомендації щодо викладання математики в 2010-2011 навчальному році, 805.17kb.
Програма з геометрії
(2 год на тиждень, у І семестрі — 32 год, у II семестрі — 38 год, усього 70 год)
| № | Тема, мета вивчення, зміст навчального матеріалу | Основні вимоги до математичної підготовки учнів |
| | Чотирикутники (24 год) | |
| І | Мета. Дати систематизовані відомості про чотирикутники та їх властивості. Чотирикутник та його елементи. Паралелограм і його властивості. Ознаки паралелограма. Прямокутник, ромб, квадрат і їх властивості. Теорема Фалеса. Середня лінія трикутника, її властивості. Трапеція. Середня лінія трапеції, її властивості. [Теорема про пропорційні відрізки. Побудова четвертого пропорційного відрізка до трьох даних відрізків]. | Учні повинні: • мати уявлення — про опуклі і неопуклі чотирикутники; • знати — означення і властивості вивчених чотирикутників; — ознаки паралелограма; — властивості середньої лінії трикутника і трапеції; • вміти — застосовувати властивості і ознаки зазначених у змісті програми чотирикутників до розв’язування задач на доведення, обчислення і побудову. |
| ІІ | Теорема Піфагора (16 год) | |
| | Мета. Сформувати апарат розв’язування прямокутних трикутників, необхідний для знаходження елементів геометричних фігур, доведення теорем планіметрії і стереометрії. Синус, косинус і тангенс гострого кута прямокутного трикутника. Теорема Піфагора. Перпендикуляр і похила. Співвідношення між сторонами і кутами прямокутного трикутника. Значення синуса, косинуса і тангенса деяких кутів. Розв’язування прямокутних трикутників. Прикладні задачі. | Учні повинні: • мати уявлення про — синус, косинус, тангенс гострого кута прямокутного трикутника; • знати — доведення теореми Піфагора; — співвідношення між сторонами і кутами прямокутного трикутника; алгоритми розв’язування прямокутних трикутників; • вміти — розв’язувати прямокутні трикутники; — застосовувати алгоритми їх розв’язування до розв’язування найпростіших прикладних задач. |
| ІІІ | Декартові координати, рухи і вектори на площині (20 год) | |
| | Мета. Повторити, систематизувати і розширити відомості про прямокутну систему координат на площині. Ознайомити учнів із елементами векторної алгебри та застосуванням методу координат у геометрії. Прямокутна система координат на площині. Координати середини відрізка. Відстань між двома точками із заданими координатами. Рівняння кола і прямої. Розміщення прямої відносно системи координат. Кутовий коефіцієнт у рівнянні прямої. Синус, косинус, тангенс кутів від 0° до 180°. Перетворення фігур. Рух та його властивості. Симетрія відносно точки і прямої. Поворот. Паралельне перенесення. [Співнапрямлені промені]. Рівність фігур. Вектор. Модуль і напрям вектора. Рівність векторів. Координати вектора. Додавання і віднімання векторів. Властивості додавання. Множення вектора на число, його властивості. Колінеарні вектори. [Кут між векторами. Скалярний добуток векторів, його властивості. Розв’язування задач за допомогою координат та векторів]. | Учні повинні: • мати уявлення про — рівняння геометричної фігури; — перетворення геометричних фігур, узагальнене поняття рівності фігур; — поняття вектора; • знати — означення понять, зазначених у змісті програми; — означення і властивості переміщень; — формули відстані між точками, координат середини відрізка; рівняння кола і прямої; — дії над векторами та їх властивості; • вміти — знаходити точку на координатній площині за її координатами та розв’язувати обернену задачу; — обчислювати за формулами відстань між двома точками, координати середини відрізка; — застосовувати властивості рухів до розв’язування простих задач; — застосовувати вектори до розв’язування простих задач. |
| IV | Резерв навчального часу (8 год) | |
9-й клас
Програма з алгебри
(3 год на тиждень у І семестрі — 48 год, 2 год на тиждень у II семестрі — 38 год, усього 86 год)
| № | Тема, мета вивчення, зміст навчального матеріалу | Основні вимоги до математичної підготовки учнів |
| І | Нерівності (18 год) | |
| | Мета. Ввести поняття числових нерівностей та обґрунтувати їх основні властивості; ввести поняття нерівності зі змінною, лінійної нерівності і систем лінійних нерівностей з однією змінною та навчити їх розв’язувати. Числові нерівності. Основні властивості числових нерівностей. Почленне додавання і множення нерівностей. Застосування властивостей числових нерівностей для оцінювання значення виразу. Нерівності зі змінними. Лінійні нерівності. Числові проміжки. Розв’язування лінійних нерівностей з однією змінною. Системи лінійних нерівностей з однією змінною, їх розв’язування. Геометрична інтерпретація множини розв’язків нерівності та систем нерівностей. Доведення нерівностей. | Учні повинні: • знати — означення числової нерівності; — властивості числових нерівностей; — означення розв’язку нерівності з однією змінною; • вміти — оцінювати значення виразів за властивостями нерівностей; — розв’язувати лінійні нерівності з однією змінною та їх системи; — давати геометричну інтерпретацію розв’язків нерівності на числовій прямій; — доводити нерівності. |
| ІІ | Квадратична функція (30 год) | |
| | Мета. Ввести поняття квадратного тричлена та його коренів; навчити розкладати квадратний тричлен на лінійні множники та виділяти з нього квадрат двочлена. Ввести означення квадратичної функції, розглянути її графік і властивості; навчити учнів розв’язувати нерівності другого степеня з однією змінною та системи рівнянь другого степеня з двома змінними; застосовувати набуті уміння до розв’язування текстових задач. Функції. Властивості функцій. Найпростіші перетворення графіків функцій. Квадратний тричлен, його корені. Розкладання квадратного тричлена на лінійні множники. Виділення квадрата двочлена із квадратного тричлена. Функція 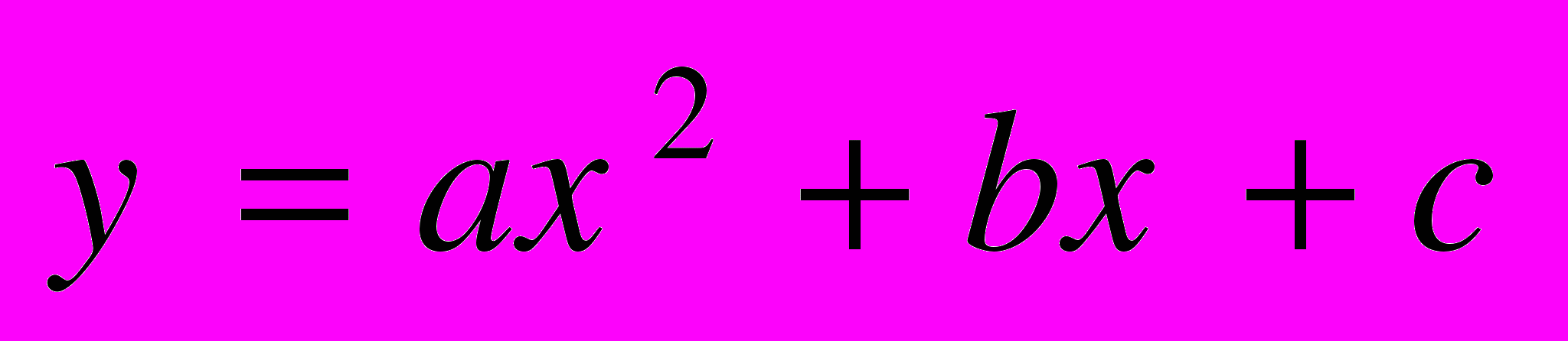 , , 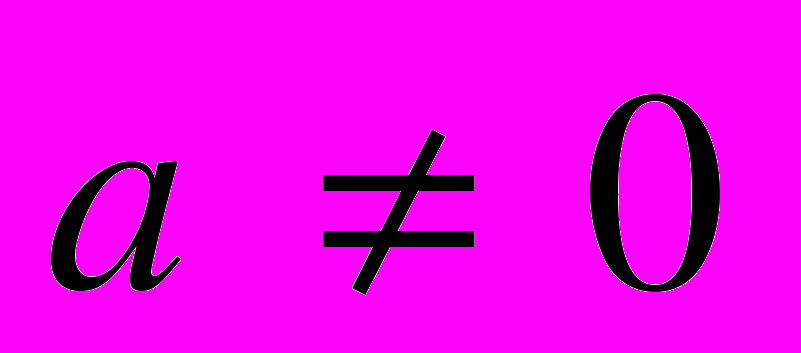 , її графік і властивості. , її графік і властивості.Квадратична нерівність. Розв’язування нерівностей другого степеня з однією змінною графічним способом. [Метод інтервалів]. Розв’язування систем рівнянь другого степеня з двома змінними. Розв’язування текстових задач за допомогою систем рівнянь. | Учні повинні: • знати — означення квадратного тричлена; — формулу розкладання квадратного тричлена на лінійні множники; — означення квадратичної функції; — формулу для обчислення абсциси вершини параболи; — алгоритм побудови графіка квадратичної функції; — означення квадратичної нерівності з однією змінною; • вміти — знаходити корені квадратного тричлена; — розкладати квадратний тричлен на лінійні множники; — будувати графік квадратичної функції; — знаходити за графіком квадратичної функції нулі функції, проміжки знакосталості, проміжки зростання і спадання функції; — розв’язувати квадратичні нерівності графічним способом [та методом інтервалів]; — розв’язувати системи рівнянь другого степеня з двома змінними. |
| ІІІ | Числові послідовності (16 год) | |
| | Мета. Ввести поняття числової послідовності, означення арифметичної і геометричної прогресій, нескінченно спадної геометричної прогресії; вивести формули п-го члена та суми перших п членів арифметичної та геометричної прогресій; суми нескінченно спадної геометричної прогресії; навчити розв’язувати вправи і задачі на застосування вивченого матеріалу. Числові послідовності. Арифметична прогресія, її властивості. Формула п-го члена арифметичної прогресії. Сума перших п членів арифметичної прогресії. Геометрична прогресія, її властивості. Формула п-го члена геометричної прогресії. Сума перших п членів геометричної прогресії. Нескінченно спадна геометрична прогресія. Сума нескінченно спадної геометричної прогресії. Періодичні дроби. Розв’язування вправ і задач на прогресії, в тому числі прикладного змісту. | Учні повинні: • мати уявлення про — числову послідовність; • знати — означення арифметичної і геометричної прогресій; — формули п-го члена арифметичної і геометричної прогресій; — формули суми перших п членів арифметичної і геометричної прогресій; • вміти — розпізнавати арифметичну і геометричну прогресії серед інших послідовностей; — знаходити будь-який член послідовності за формулою п-го члена; — знаходити суму перших п членів арифметичної і геометричної прогресій; — розв’язувати задачі на арифметичну і геометричну прогресії. |
| IV | Елементи прикладної математики (10 год) | |
| | Мета. Ввести поняття про математичне моделювання. Розглянути загальну задачу математичного моделювання, проілюструвати прикладами. Ввести поняття про наближене значення чисел і величин, абсолютну та відносну похибки, правильну цифру наближення, оцінку похибок. Сформулювати правила арифметичних дій з наближеними значеннями за способом підрахунку правильних цифр та навчити застосовувати їх під час розв’язування задач. Математичне моделювання. Приклади математичного моделювання. Наближені значення чисел і величин. Абсолютна [і відносна] похибки наближення. Оцінка похибок. Додавання, віднімання, множення і ділення наближених значень. Відсоткові розрахунки. Формули простих і складних відсотків. | Учні повинні: • мати уявлення про — математичне моделювання і його загальну задачу; — наближені значення чисел і величин; — абсолютну [і відносну] похибки, точність наближення; • знати — правила округлення чисел, виконання арифметичних дій з наближеними значеннями; — правила подання відповіді до прикладної задачі; • вміти — складати моделі до прикладних задач та розв’язувати їх; — знаходити абсолютну [і відносну] похибки, точність наближення; — виконувати дії над наближеними значеннями, в тому числі і за допомогою комп’ютера; — застосовувати набуті знання до розв’язування прикладних задач; — розв’язувати найпростіші задачі на відсоткові розрахунки. |
| V | Повторення і систематизація навчального матеріалу (12 год) | |
