Програми для загальноосвітніх навчальних закладів Математика

Вид материала

Документы

Содержание Найпростіші геометричні фігури та їх властивості (12 год) Учні повинні Трикутники (20 год) Учні повинні Геометричні побудови (14 год) Учні повинні Резерв навчального часу (8 год) Раціональні вирази (30 год) Учні повинні Квадратні корені. Дійсні числа (18 год) Учні повинні Квадратні рівняння (20 год) Учні повинні Функції (12 год) Резерв навчального часу (6 год)

Подобный материал:

• Атики в 5-9 класах загальноосвітніх навчальних закладів вивчатиметься за програмами,, 164.05kb.
• Особливості навчальної програми для учнів 8 класу загальноосвітніх навчальних закладів, 602.24kb.
• «Математика в школі», 894.13kb.
• «Математика в школі», 804.81kb.
• Програма для загальноосвітніх навчальних закладів (класів) з поглибленим вивченням, 717.77kb.
• Програми та рекомендації до розподілу програмного матеріалу загальноосвітніх навчальних, 2950.56kb.
• Програми та рекомендації до розподілу програмного матеріалу загальноосвітніх навчальних, 2719.13kb.
• Програми та рекомендації до розподілу програмного матеріалу загальноосвітніх навчальних, 1209.62kb.
• Програми та рекомендації до розподілу програмного матеріалу загальноосвітніх навчальних, 2778.79kb.
• Методичні рекомендації щодо викладання математики в 2010-2011 навчальному році, 805.17kb.

Програма з геометрії

(1 год на тиждень у І семестрі — 16 год, 2 год на тиждень у II семестрі — 38 год, усього 54 год)

№	Тема, мета вивчення, зміст навчального матеріалу	Основні вимоги до математичної підготовки учнів
1	Найпростіші геометричні фігури та їх властивості (12 год)
	Мета. Систематизувати наочні уявлення учнів про основні властивості найпростіших геометричних фігур. Геометрична фігура. Точка і пряма та їх властивості. Відрізок. Основні властивості вимірювання відрізків. [Півплощина.] Півпряма. Кут. Основні властивості вимірювання кутів. [Відкладання відрізків і кутів]. Трикутник. Рівні трикутники. [Існування трикутника, що дорівнює даному]. Суміжні і вертикальні кути, їх властивості. Бісектриса кута. Паралельні і перпендикулярні прямі та їх властивості.[Доведення від супротивного. Аксіома. Теорема, її доведення].	Учні повинні: • мати уявлення про — аксіоми, теореми, доведення; • знати — означення геометричних фігур, вказаних у змісті програми; — основні властивості належності точок і прямих, взаємного розміщення точок на прямій і на площині, вимірювання та відкладання відрізків і кутів, паралельних і перпендикулярних прямих; — теореми про суміжні і вертикальні кути; • вміти — зображати та знаходити на малюнках точки, прямі, відрізки, півпрямі, встановлювати і характеризувати взаємне розміщення вказаних у змісті фігур; — застосовувати одержані знання до розв’язування задач на обчислення і доведення.
ІІ	Трикутники (20 год)
	Мета. Розширити відомості про трикутники та їх властивості, паралельні та перпендикулярні прямі; ознайомити учнів з ознаками рівності трикутників; виробити вміння доводити рівність трикутників, спираючись на ознаки. Ознаки рівності трикутників. Рівнобедрений трикутник та його властивість. [Обернена теорема.] Висота, бісектриса і медіана трикутника. Властивість медіани рівнобедреного трикутника. Кути, утворені при перетині двох прямих січною. Ознаки паралельності прямих. Властивості кутів, утворених при перетині паралельних прямих січною. Сума кутів трикутника. Зовнішній кут трикутника та його властивості. Прямокутний трикутник. [Ознаки рівності прямокутних трикутників]. Існування і єдиність перпендикуляра до прямої.	Учні повинні: • мати уявлення про — рівність трикутників, термін «ознака»; • знати — означення різних видів трикутників; — означення бісектриси, висоти, медіани трикутника та їх властивості; — властивість рівнобедреного трикутника; — ознаки рівності трикутників; — ознаки паралельних прямих; — властивості кутів, утворених при перетині паралельних прямих січною; — суму внутрішніх кутів трикутника; — властивість зовнішнього кута трикутника; • вміти — зображати та знаходити на малюнках рівносторонні, рівнобедрені, прямокутні трикутники та їх елементи; — застосовувати властивості трикутників та їх елементів, паралельних прямих, кутів, утворених при перетині паралельних прямих січною до розв’язування задач; — доводити рівність трикутників, паралельність прямих, спираючись на відповідні ознаки.
ІІІ	Геометричні побудови (14 год)
	Мета. Дати систематизовані відомості про коло і фігури, пов’язані з ним. Ознайомити учнів з поняттям задачі на побудову; сформувати вміння розв’язувати основні задачі на побудову за допомогою циркуля і лінійки. Коло. [Властивості серединного перпендикуляра відрізка]. Коло, описане навколо трикутника. Дотична до кола, її властивості. [Властивість бісектриси кута]. Коло, вписане в трикутник. Основні задачі на побудову: — побудова трикутника за трьома сторонами; — побудова кута, що дорівнює даному; — побудова бісектриси даного кута; — поділ даного відрізка навпіл; — побудова перпендикулярної прямої; — побудова паралельних прямих. Поняття про геометричне місце точок. [Метод геометричних місць].	Учні повинні: • мати уявлення про — побудову геометричної фігури за допомогою циркуля і лінійки; • знати — означення кола, радіуса, діаметра і хорди, дотичної до кола; властивість дотичної до кола; — способи виконання основних побудов; • вміти — зображати на малюнках коло та його елементи; — застосовувати властивості вписаного (описаного) кола до розв’язування задач; — розв’язувати основні задачі на побудову.
IV	Резерв навчального часу (8 год)

8-й клас

Програма з алгебри

(3 год на тиждень у І семестрі — 48 год, 2 год на тиждень у II семестрі — 38 год, усього 86 год)

№	Тема, мета вивчення, зміст навчального матеріалу	Основні вимоги до математичної підготовки учнів
І	Раціональні вирази (30 год)
	Мета. Ввести поняття степеня з цілим показником та його властивості, алгебраїчного дробу, раціонального виразу і дробового раціонального виразу; навчити виконувати тотожні перетворення дробів і раціональних виразів. Ділення степенів. Алгебраїчні дроби, раціональні вирази і дробові раціональні вирази. Допустимі значення змінних. Основна властивість дробу. Скорочення дробів. Додавання і віднімання дробів. Множення дробів. Піднесення дробу до степеня. Ділення дробів. Степінь з цілим показником і його властивості. Стандартний вигляд числа. Тотожні перетворення раціональних виразів. Раціональні рівняння.	Учні повинні: • мати уявлення про — степінь з нульовим показником, цілим від’ємним показником, його властивості; — стандартний вигляд числа; — алгебраїчний дріб, раціональний і дробовий вирази; — тотожні перетворення виразів із алгебраїчними дробами; — раціональні рівняння; • знати — правила виконання дій над степенями з цілим показником; — правило ділення степенів з цілим показником; — основну властивість дробу; • вміти — спрощувати числові і найпростіші буквені вирази з цілим показником; — записувати числа в стандартному вигляді; — розпізнавати алгебраїчний дріб серед інших буквених виразів; — використовувати основну властивість алгебраїчного дробу; — знаходити суму, різницю, добуток і частку двох алгебраїчних дробів; — виконувати тотожні перетворення раціональних виразів: — розв’язувати нескладні раціональні рівняння.
ІІ	Квадратні корені. Дійсні числа (18 год)
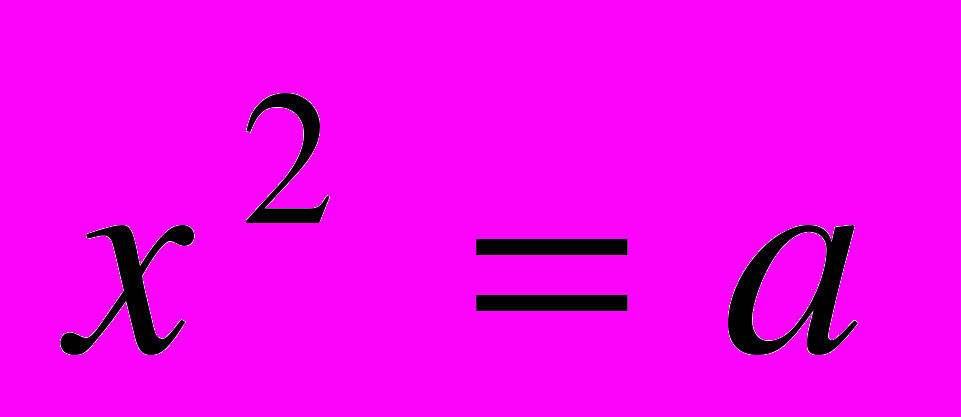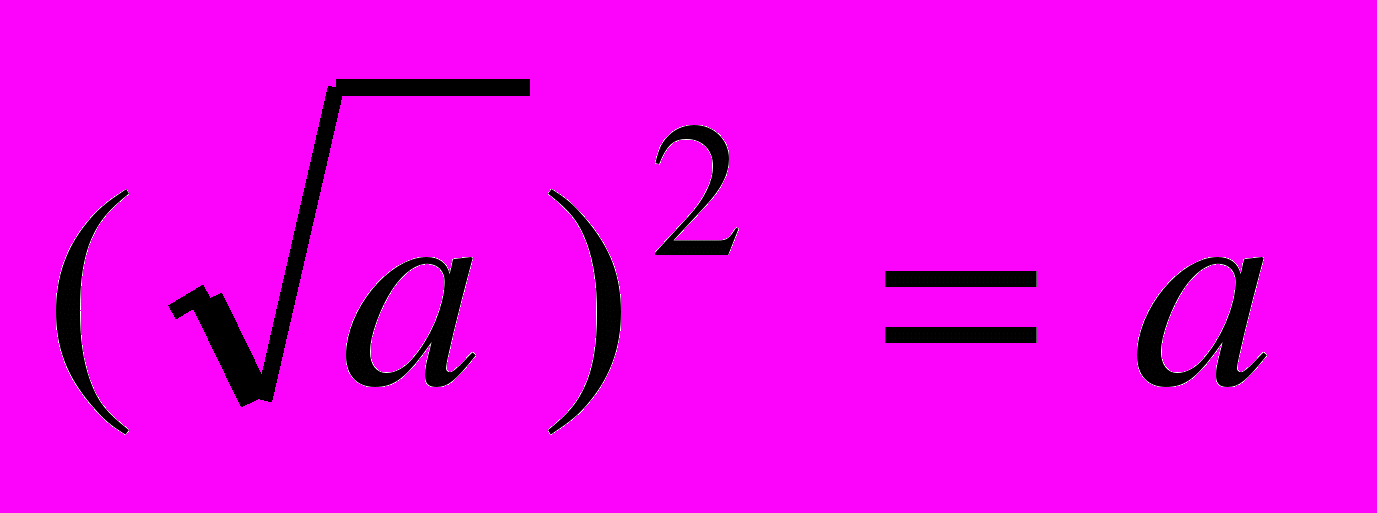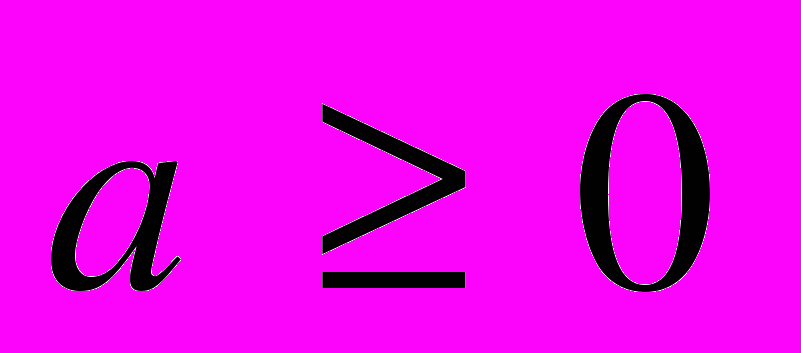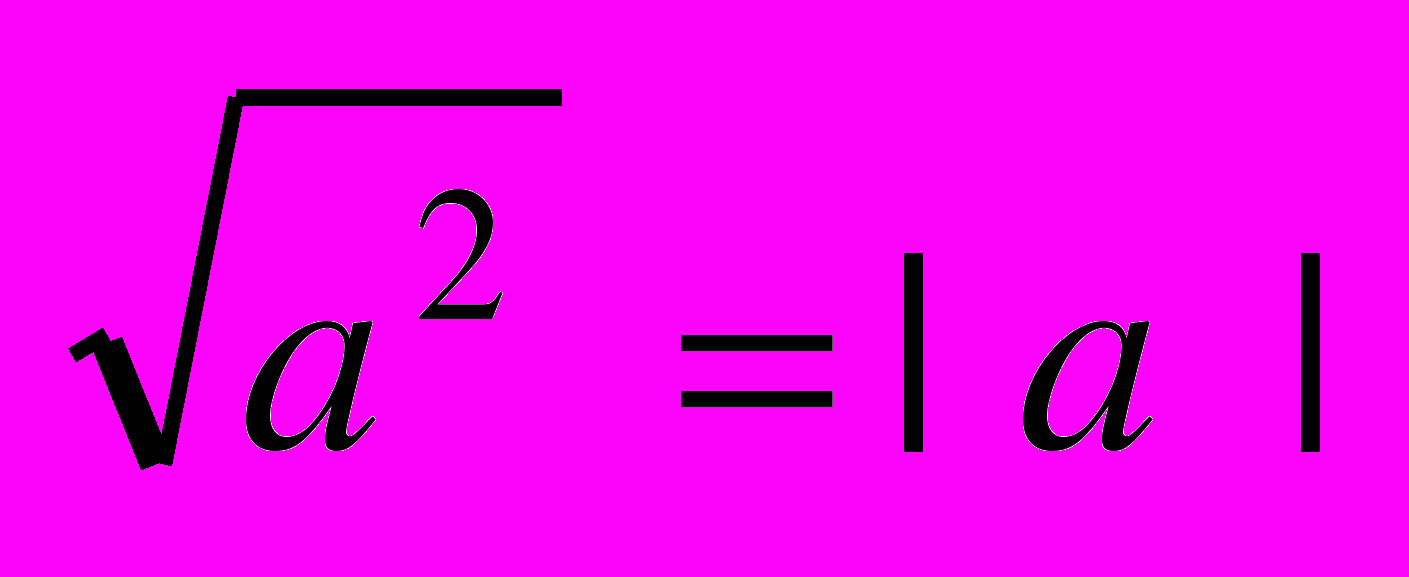	Мета. Ввести поняття квадратного кореня, арифметичного квадратного кореня і його властивості; ірраціонального числа і дійсного числа; навчити виконувати тотожні перетворення виразів, що містять квадратні корені. Квадратні корені. Арифметичний квадратний корінь і його властивості. Рівняння . Ірраціональні числа. Дійсні числа. Тотожності , ; . Квадратний корінь з добутку, частки і степеня. Перетворення виразів, що містять квадратні корені.	Учні повинні: • мати уявлення про — квадратний корінь; — арифметичний квадратний корінь; — розширення поняття числа; — ірраціональні та дійсні числа: • знати — властивості арифметичного квадратного кореня; — тотожності 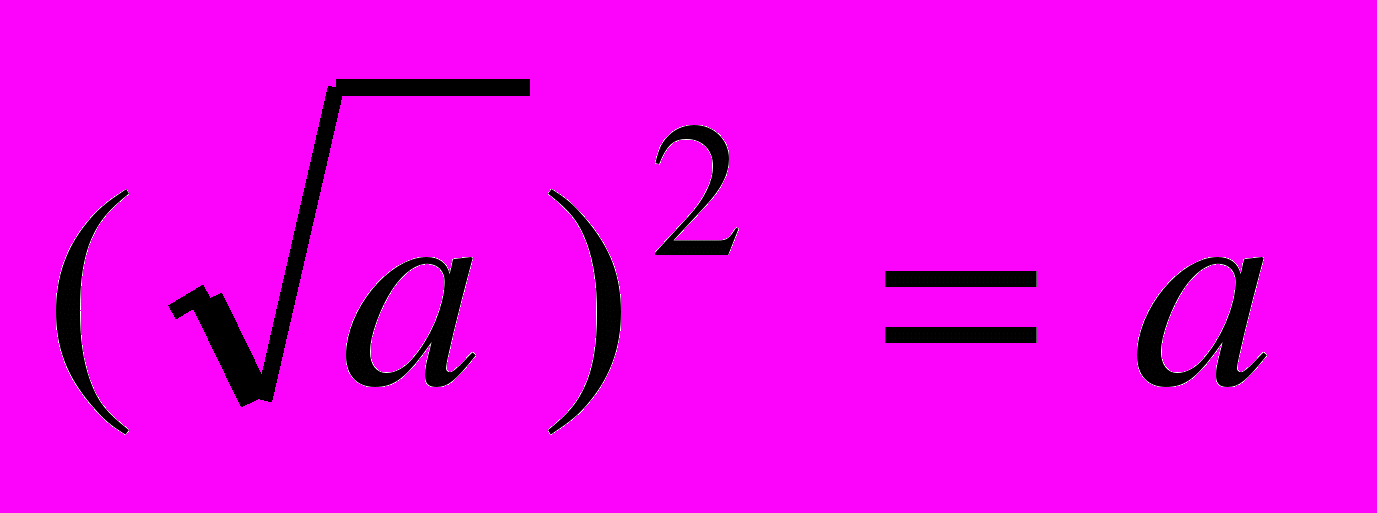, 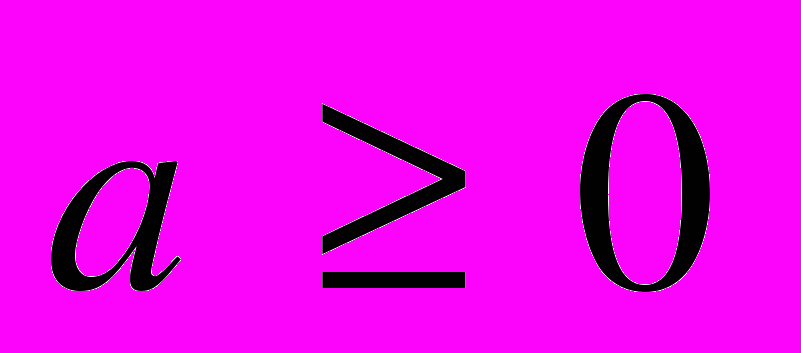; ; 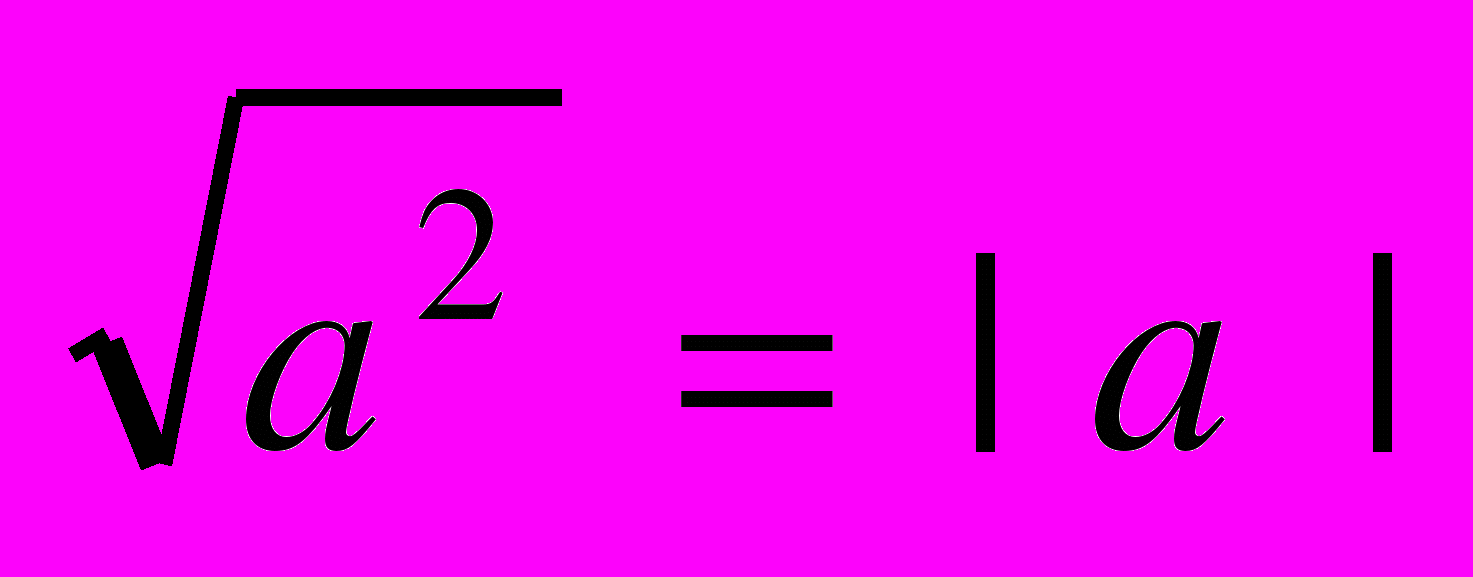• вміти — знаходити значення арифметичного квадратного кореня; — застосовувати властивості арифметичного квадратного кореня для спрощення виразів.
ІІІ	Квадратні рівняння (20 год)
	Мета. Ввести означення квадратного рівняння і вивести формулу його коренів; сформувати вміння розв’язувати квадратні рівняння і застосовувати їх до розв’язування задач. Квадратні рівняння. Неповні квадратні рівняння, їх розв’язування. Формула коренів квадратного рівняння. Теорема Вієта. Розв’язування рівнянь, що зводяться до квадратних. Розв’язування задач за допомогою квадратних рівнянь.	Учні повинні: • знати — означення квадратного рівняння; — формули дискримінанта, коренів квадратного рівняння; — залежність між значенням дискримінанта та кількістю коренів квадратного рівняння; • вміти — розпізнавати квадратні рівняння серед інших рівнянь; — розв’язувати неповні квадратні рівняння, квадратні рівняння за формулою коренів квадратного рівняння; — знаходити суму та добуток коренів зведеного квадратного рівняння за теоремою Вієта; — розв’язувати раціональні рівняння, що зводяться до квадратних рівнянь; — розв’язувати нескладні, зокрема біквадратні рівняння за допомогою заміни змінної; — розв’язувати нескладні текстові задачі на складання квадратних рівнянь і рівнянь, що зводяться до квадратних.
IV	Функції (12 год)
	Мета. Ввести поняття функції, області визначення і області значень функції; способи задання функції; розглянути функції, зазначені в програмі, їх графіки та властивості. Функція. Аргумент і значення функції. Область визначення і область значень функції. Способи задання функції. Графік функції. Лінійна функція. Графік лінійної функції, її властивості. Функці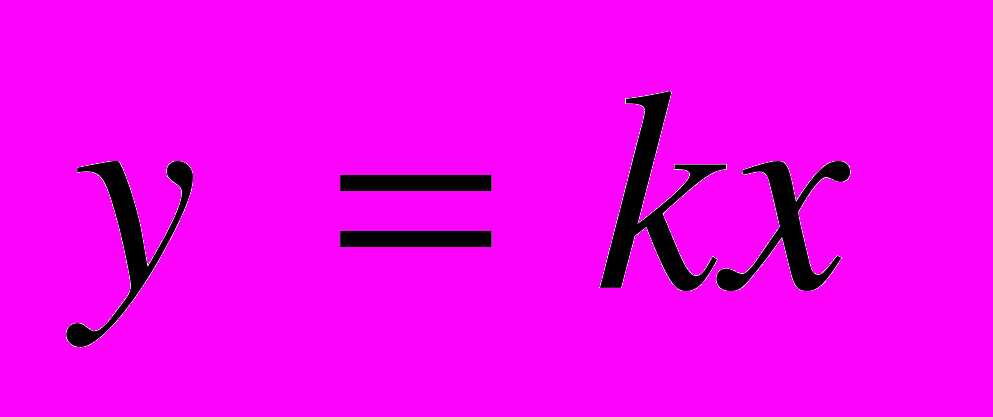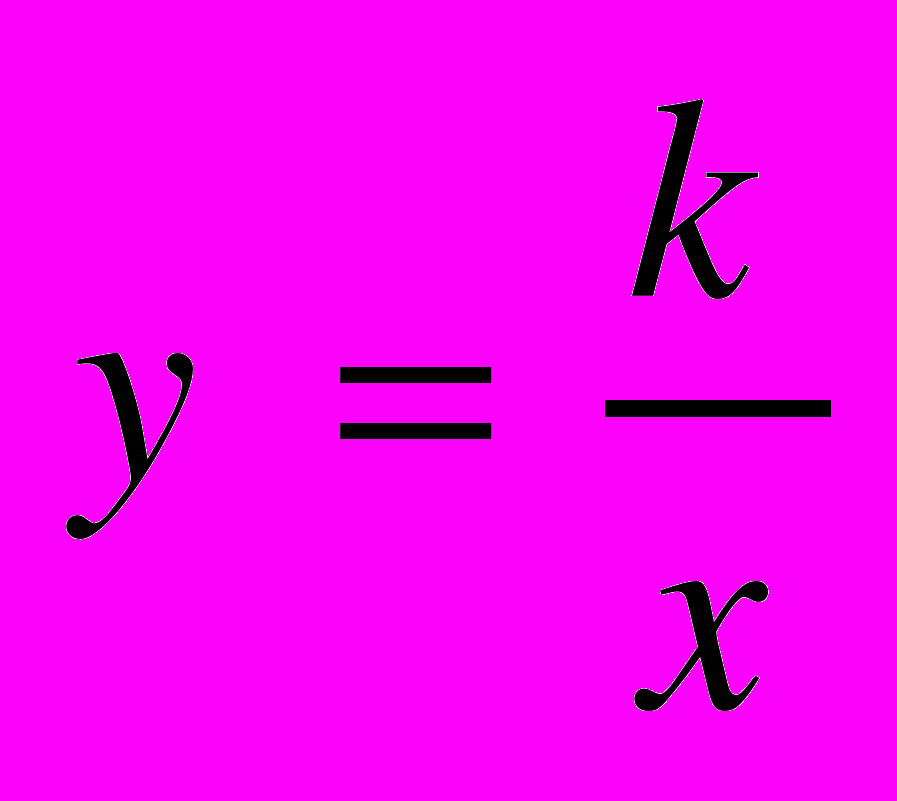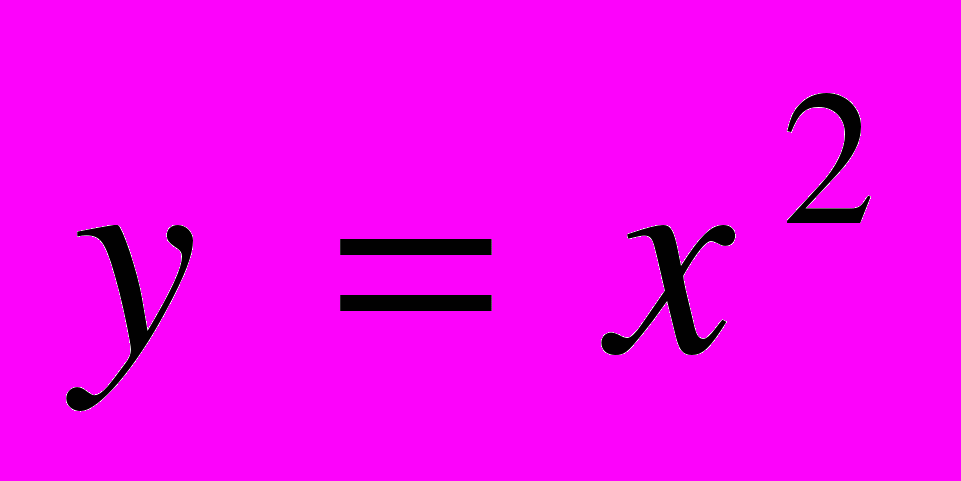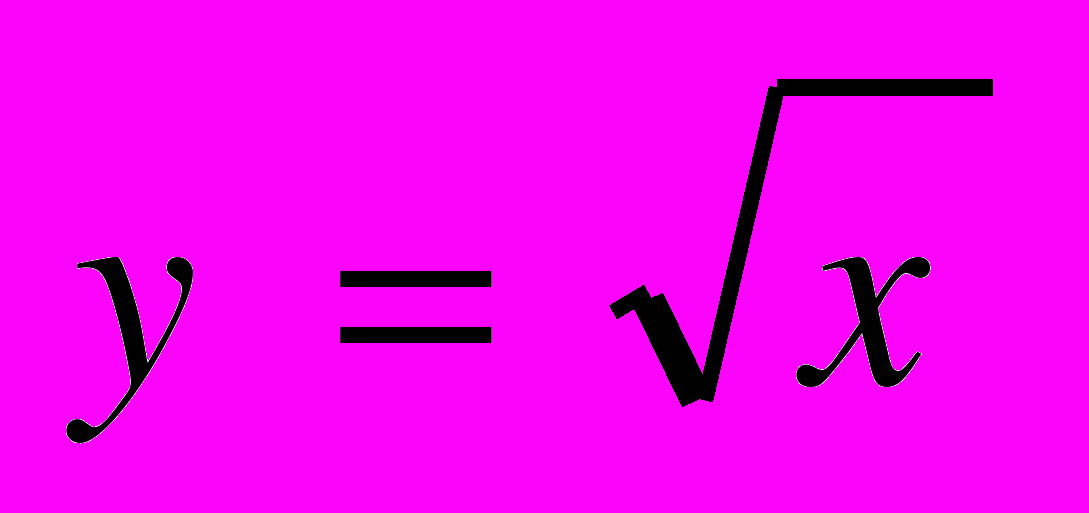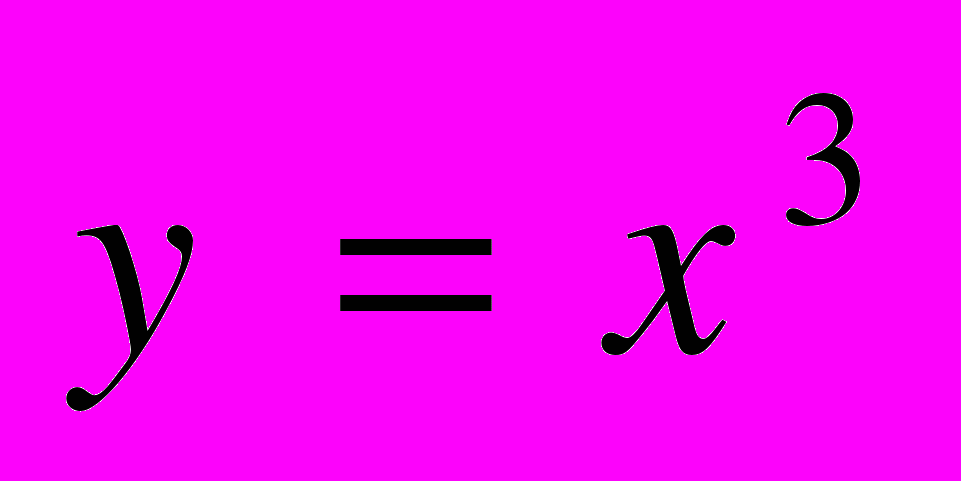ї , , , , [], їх графіки і властивості.	Учні повинні: • мати уявлення про — функцію, аргумент і значення функції, область визначення, область значень, нулі функції, графік функції; • знати — означення функції; — три основні способи задання функції; — означення лінійної функції, прямої і оберненої пропорційностей; — основні властивості зазначених функцій та функцій 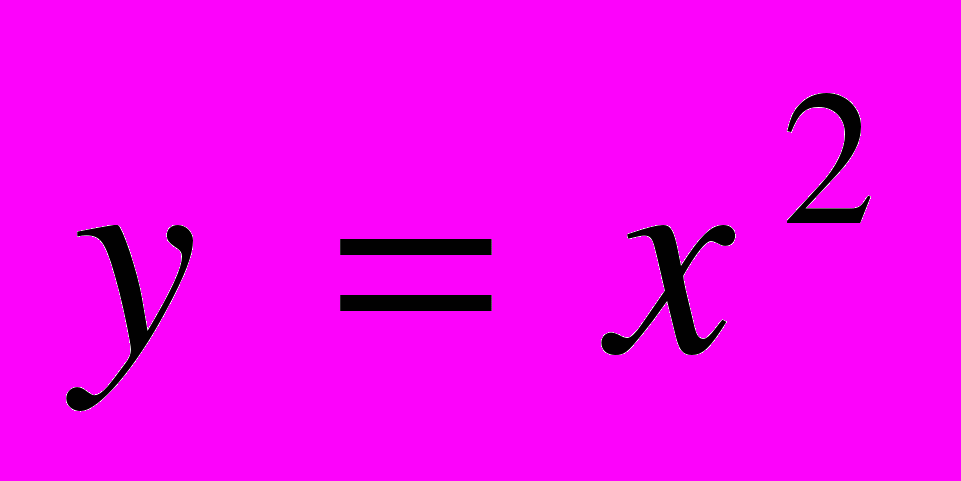, , 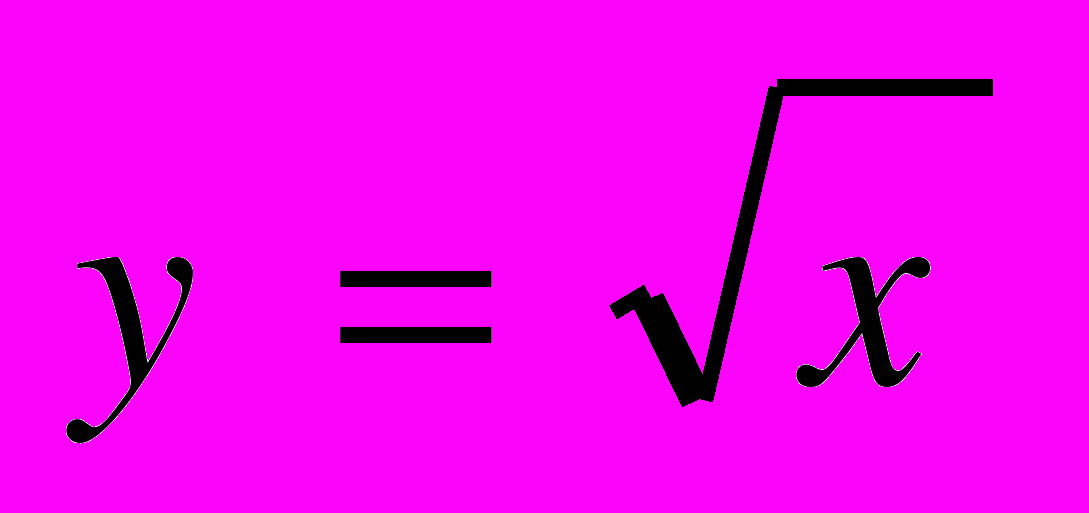[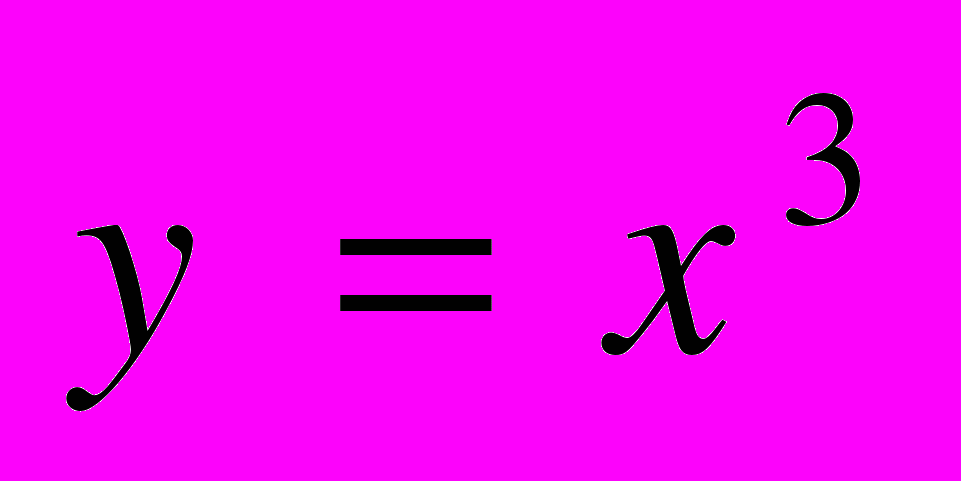]; — знаходити область значення і область значень функції; — знаходити значення функції, заданої графіком, таблицею або формулою; — будувати графіки зазначених функції.
V	Резерв навчального часу (6 год)