Geum.ru

Програми для загальноосвітніх навчальних закладів Математика

Вид материалаДокументы

Содержание


Подільність чисел (14 год)
Учні повинні
Звичайні дроби (30 год)
Учні повинні
Відношення і пропорції (20 год)
Учні повинні
Геометричні фігури (20 год)
Учні повинні
Раціональні числа та дії над ними (60 год)
Учні повинні
Повторення і систематизація навчального матеріалу (15 год)
Подобный материал:
1   2   3   4   5   6   7   8   9   ...   12
Програма з математики

(4 год на тиждень у І семестрі — 64 год, 5 год на тиждень у II семестрі — 95 год, усього 159 год)

№
Тема, мета вивчення, зміст навчального матеріалу
Основні вимоги до математичної підготовки учнів

І
Подільність чисел (14 год)






Мета. Продовжити вивчення

натуральних чисел, підготувати основу для засвоєння дій із звичайними дробами.

Дільники натурального числа. Парні й непарні натуральні числа. Подільність чисел. Ознаки подільності на 2, 5 і 10.

Ознаки подільності на 3 і 9. Прості і складені числа.

Розкладання чисел на прості

множники. Спільні дільники кількох чисел. Найбільший спільний дільник. Взаємно прості числа. Спільне кратне кількох чисел. Найменше спільне кратне.
Учні повинні:

• мати уявлення про

— подільність чисел;

— прості і складені числа;

• знати

— означення дільника, кратного, простого і складеного чисел, найбільшого спільного дільника і

найменшого спільного кратного;

— ознаки подільності на 2, 3, 5, 9, 10;

• вміти

— розпізнавати парні і непарні числа;

— розкладати натуральні числа (у межах тисячі) на прості множники;

— користуватися ознаками подільності чисел на 2, 3, 5, 9, 10;

— знаходити спільні дільники та спільні кратні двох-трьох чисел; найбільший спільний дільник (НСД) і найменше спільне кратне (НСК) двох чисел.

ІІ
Звичайні дроби (30 год)






Мета. Сформувати міцні навички виконання чотирьох арифметичних дій над звичайними дробами, розв’язування текстових задач на дроби.

Повторення відомостей про звичайні дроби. Основна властивість дробу. Скорочення дробу. Найменший спільний знаменник. Зведення дробів до спільного знаменника. Порівняння дробів.

Додавання і віднімання звичайних дробів. Додавання і віднімання цілих і дробових чисел.

Множення звичайних дробів. Множення цілих і дробових чисел. Знаходження дробу від числа.

Взаємно обернені числа. Ділення дробів. Ділення цілих і дробових чисел. Знаходження числа за його дробом.

Перетворення звичайних дробів у десяткові і навпаки. [Нескінченні періодичні десяткові дроби].

Розв’язування текстових задач.
Учні повинні:

• мати уявлення про звичайний дріб;

• знати

— основну властивість дробу та

ілюструвати її на прикладах;

— правила додавання, віднімання, множення і ділення дробів;

— правила знаходження дробу від числа та числа за його дробом;

• вміти

— читати і записувати звичайні дроби;

— застосовувати основну властивість дробу до скорочення дробів і зведення дробів до спільного знаменника;

— додавати і віднімати звичайні дроби, виконувати множення і ділення звичайних дробів;

— порівнювати дроби;

— записувати звичайні дроби у вигляді десяткових і навпаки;

— розв’язувати основні задачі на дроби.

ІІІ
Відношення і пропорції (20 год)






Мета. Сформувати поняття відношення, пропорції, прямої [і оберненої] пропорційних залежностей; навчити розв’язувати задачі на використання основної властивості пропорції та використання прямої [і оберненої] пропорційних залежностей; розв’язувати три основні задачі на відсотки.

Відношення. Основна властивість відношення.

Пропорція. Члени пропорції. Основна властивість пропорції. Розв’язування рівнянь на основі властивості пропорції.

Відсоткове відношення двох чисел. Знаходження відсоткового відношення двох чисел. Відсоткові розрахунки.

Пряма [і обернена] пропорційні залежності. Задачі на пропорційний поділ. Розв’язування задач на пряму [і обернену] пропорційні залежності.
Учні повинні:

• мати уявлення про відношення, пропорцію, пряму [і обернену] пропорційність величин;

• знати

— означення відсотка (процента), відношення і пропорції,

— основну властивість пропорції;

• вміти

— записувати відсотки у вигляді звичайного і десяткового дробів та будь-яке число у вигляді відсотка;

— розв’язувати три основні задачі на відсотки;

— знаходити невідомий член пропорції;

— розв’язувати задачі на пропорційні величини.

IV
Геометричні фігури (20 год)






Мета. Продовжити формувати на наочно-оперативному рівні уявлення про основні геометричні фігури та їх властивості. Навчити обчислювати геометричні величини за формулами.

Перпендикулярні і паралельні прямі. Побудова перпендикулярних і паралельних прямих за допомогою лінійки і косинця.

Паралелограм. Площа трикутника і паралелограма. Коло. Довжина кола. Круг. Площа круга. Круговий сектор. Кругові діаграми.

Пряма призма. Основа і висота призми. Розгортка поверхні призми. Формули площі поверхні і об’єму прямої призми.

Циліндр. Основа і висота циліндра. Розгортка поверхні циліндра. Формули площі поверхні і об’єму циліндра.

Куля. Центр, радіус, діаметр кулі. [Формули площі поверхні і об’єму кулі.]
Учні повинні:

• мати уявлення про

— перпендикулярні і паралельні прямі;

— паралелограм, коло, круг, пряму призму, циліндр, кулю;

— розгортку поверхні призми і циліндра;

• знати

— назви зазначених у змісті геометричних фігур;

— формули довжини кола і площі круга;

— наближене значення числа ;

— формули площі поверхні та об’єму прямої призми, циліндра;

• вміти

— будувати перпендикуляр до прямої і паралельні прямі за допомогою лінійки і косинця;

— обчислювати за формулами довжину кола, площу паралелограма, трикутника, круга, площу поверхні прямої призми, циліндра;

— обчислювати за формулами об’єм прямої призми, циліндра.

V
Раціональні числа та дії над ними (60 год)






Мета. Розширити уявлення учнів про число шляхом введення від’ємних чисел. Сформувати навички виконання чотирьох арифметичних дій над додатними і від’ємними числами, обчислення значень виразів, що містять додатні і від’ємні числа.

Додатні та від’ємні числа. Число 0.

Координатна пряма.

Протилежні числа. Модуль числа. Відстань між двома точками на координатній прямій.

Цілі числа. Раціональні числа.

Порівняння раціональних чисел.

Знаки «», «».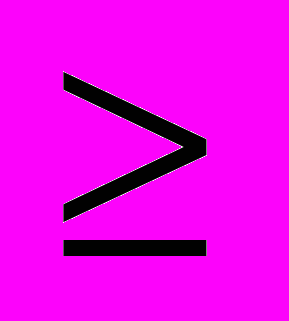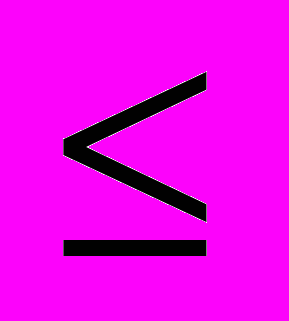

Додавання раціональних чисел.

Властивості додавання.

Віднімання раціональних чисел.

Заміна віднімання додаванням.

Множення раціональних чисел.

Квадрат і куб від’ємного числа.

Властивості множення. Розкриття дужок.

Подібні доданки та їх зведення.

Ділення раціональних чисел.

Рівняння. Основна властивість рівняння. Розв’язування задач за допомогою рівнянь.

Координатна площина. Абсциса і координата точки. Приклади графіків залежностей між величинами.
Учні повинні:

• мати уявлення про

— додатні та від’ємні числа і нуль;

— протилежні числа; модуль числа;

— координатну пряму; прямокутну систему координат на площині;

— числові і буквені вирази;

— коефіцієнт;

— подібні доданки;

• знати

— що нуль не належить ні до додатних, ні до від’ємних чисел;

— правила виконання чотирьох арифметичних дій над додатними і

від’ємними числами, властивості дій;

— правило перенесення членів рівняння з однієї частини в іншу;

— правила розкриття дужок і зведення подібних доданків;

назви координат;

• вміти

— розрізняти додатні і від’ємні числа;

— знаходити і записувати число,

протилежне даному;

— будувати координатну пряму;

зображати раціональні числа на

координатній прямій;

— знаходити і записувати координати точок на прямій і виконувати обернену задачу;

— знаходити і записувати значення

модуля числа;

— порівнювати раціональні числа;

— виконувати додавання і віднімання, множення і ділення раціональних чисел;

— обчислювати значення числових

виразів, що містять додатні і від’ємні числа;

— розкривати дужки, зводити подібні доданки;

— розв’язувати нескладні рівняння з однією змінною та застосовувати їх до розв’язування текстових задач;

— знаходити точку на координатній площині за даними її координатами і розв’язувати обернену задачу.

VI
Повторення і систематизація навчального матеріалу (15 год)




7-й клас