Geum.ru

Програми для загальноосвітніх навчальних закладів Математика

Вид материалаДокументы
Подобный материал:
1   2   3   4   5   6   7   8   9   ...   12
Алгебра

Мета вивчення алгебри в 7—9-х класах — удосконалення обчислювальних навичок; формування в учнів навичок виконання тотожних перетворень різних видів виразів, розв’язування рівнянь і нерівностей; засвоєння апарату рівнянь і нерівностей як основного засобу математичного моделювання прикладних задач; формування поняття функції і вивчення властивостей функцій, зазначених у програмі; застосування одержаних знань і умінь до вивчення суміжних предметів (фізики, хімії, основ інформатики та обчислювальної техніки тощо.)

Шкільний курс алгебри істотно відрізняється від сучасної науки алгебри (науки про групи, кільця, поля та інші алгебраїчні структури).

Шкільна алгебра складається з кількох провідних ліній:

— числа і обчислення,

— вирази та їх перетворення,

— рівняння, нерівності та їх системи,

— функції і графіки,

— елементи прикладної математики.

Алгебру в 7-му класі краще починати з вивчення рівнянь. Це дає можливість переконливо і легко мотивувати вивчення перших розділів: рівняння треба вміти розв’язувати для розв’язування важливих задач, а вирази перетворювати — щоб уміти розв’язувати нові види рівнянь. Така послідовність вивчення перших розділів алгебри дає змогу вже на перших уроках пояснити походження назви «алгебра», а також полегшити навчальний процес і зробити його продуктивнішим.

Дотримуючись принципів науковості і доступності навчання, на уроках алгебри бажано пропонувати учням означення деяких понять і обґрунтування найважливіших тверджень. Але не слід строго означати поняття «вираз», «рівняння», «формула». Не обов’язково розглядати в основній школі, що таке алгебраїчний вираз, алгебраїчний дріб, алгебраїчне рівняння, алгебраїчне число.

Бажано розрізняти квадратні рівняння і рівняння, які зводяться до квадратних. Немає потреби вводити термін «повне квадратне рівняння», формула коренів правильна для будь-яких квадратних рівнянь, зокрема і неповних. Теорему Вієта можна розглядати тільки для зведених квадратних рівнянь. Формули коренів квадратного рівняння можна виводити різними способами. Учитель може обрати той спосіб, який йому здається кращим. Це стосується також доведення інших теорем і формул.

Наближені обчислення в програмі пропонуються в дещо зменшеному обсязі. Із появою мікрокалькуляторів та інших ЕОМ їх роль істотно змінилася, тепер досить навчити учнів грамотно округляти числа. Про обчислення з точним урахуванням похибок досить дати тільки уявлення, застосовуючи подвійні нерівності.
Алгебра і початки аналізу

Мета вивчення алгебри і початків аналізу в 10—11-х класах — систематичне вивчення функцій засобами алгебри і математичного аналізу. Вивчаючи властивості тригонометричних, показникової, логарифмічної, степеневої функцій, учні повинні навчитися виконувати відповідні тотожні перетворення виразів і застосовувати їх до розв’язування тригонометричних, показникових, логарифмічних, ірраціональних рівнянь і нерівностей. Засвоєння понять похідної, первісної, інтеграла дасть змогу досліджувати елементарні функції, розв’язувати найпростіші геометричні, фізичні та інші задачі прикладного змісту.

Матеріал з алгебри і початків аналізу програма пропонує в мінімальному обсязі, враховуючи, що на його вивчення відводиться тільки 2 год на тиждень. Якщо вчитель має можливість виділити більше годин, то можна повніше розглянути питання про границю і неперервність функції, диференціальні рівняння, теорії ймовірностей і математичної статистики.

Опрацьовуючи розділ «Тригонометричні функції», не слід намагатися доводити і примушувати учнів запам’ятовувати всі формули, які традиційно розглядалися раніше. Важлива і потрібна наука в минулому, сьогодні тригонометрія втратила свою колишню роль. І логарифми у зв’язку з поширенням мікрокалькуляторів відійшли в історію. Також розв’язування сотень тригонометричних, логарифмічних, показникових рівнянь, непов’язаних з будь-якими прикладними задачами, — традиція, від якої бажано поступово звільнятися. Вивільнені години доцільно використати для розв’язування важливих прикладних задач.
Геометрія

Мета вивчення геометрії в 7—9-х класах — систематичне вивчення властивостей геометричних фігур та їх перетворення на площині; формування просторових уявлень і уяви, розвиток логічного мислення і використання геометричного апарату для вивчення суміжних предметів (фізика, креслення, географія, трудове навчання та ін.) У цьому курсі учні розширюють свої знання про координатний метод і ознайомлюються з векторами на площині та їх застосуванням до розв’язування задач, тригонометричними функціями та їх застосуванням до розв’язування трикутників.

Мета вивчення геометрії в 10—11-х класах — систематичне вивчення властивостей просторових геометричних фігур; розвиток просторових уявлень і уяви; засвоєння способів зображення просторових фігур на площині; обчислення площ поверхонь і об’ємів геометричних тіл і подальший розвиток логічного мислення.

У процесі вивчення стереометричного матеріалу систематизуються, узагальнюються і закріплюються геометричні знання, навички і вміння, одержані під час вивчення планіметрії в 7—9-х класах. Прикладна спрямованість вивчення матеріалу забезпечується широким використанням наочності, зверненням до життєвого досвіду учнів, розв’язуванням задач практичного змісту.

У 7—11-х класах загальноосвітньої школи учні вивчають досвідно-дедуктивний курс геометрії. Його основні поняття запозичуються з досвіду, а обґрунтування теорем пропонуються дедуктивні з використанням неповної системи аксіом. Були спроби вже на початку вивчення геометрії формулювати всі аксіоми, достатні для побудови геометрії, і дотримуватися строгого аксіоматичного викладу. Але такий курс геометрії для учнів виявився надто абстрактним, формальним і непривабливим. Багаторічний досвід показав, що в загальноосвітній школі спочатку краще формулювати тільки частину аксіом і не дотримуватися строгого аксіоматичного викладу. Не виправдала себе і надмірна переоцінка ролі доведень за рахунок недооцінки інших складових частин геометрії: геометричних понять, їх означень і класифікацій, геометричних фігур і їх побудов, вимірювань і обчислень. За висловенням Д.Гільберта справжня геометрія схожа на гарний сад, а «у величезному саду геометрії кожний може підібрати собі букет за смаком». То, якщо один учитель більше полюбляє геометричні побудови, інший — означення і класифікації геометричних понять, ще інший — теореми і їх доведення чи розв’язування цікавих геометричних задач, то нехай кожний прививає любов учнів до того, що йому найбільше до вподоби. Це зробить навчання геометрії набагато цікавішим і ефективнішим, ніж коли всі будуть дбати тільки про доведення.

Не обов’язково всі теореми, передбачені програмою, доводити за традиційною схемою: «Дано... Довести... Доведення». Принаймні половину їх можна доводити інскриптивним методом, напівусно. Бажано також усно чи напівусно розв’язувати якомога більше геометричних задач, і не тільки в молодших і середніх класах.

Розділ «Елементи стереометрії» у 9-му класі пропонується для того, щоб випускники основної школи, які не продовжуватимуть навчання в старших класах, мали хоч деякі уявлення про просторові фігури, про обчислення об’ємів і площ поверхонь найважливіших геометричних тіл. Інше його призначення — пропедевтичне (для підготовки до вивчення геометрії в старших класах).

Формули для знаходження об’ємів геометричних тіл у 11-му класі можна виводити різними способами: з використанням границь, інтегралів чи аксіом Кавальєрі. Учитель може обрати той спосіб, який йому здається кращим.

Традиційне виведення формул для обчислення площ поверхонь тіл обертання (на основі різних означень для різних тіл) містить приховану логічну помилку. Тому в слабших класах ці формули краще виводити через розгортки, а в сильніших — на основі загального означення площі поверхні (як границі відношення об’єму шару товщини t цієї поверхні до t за умови, що ).
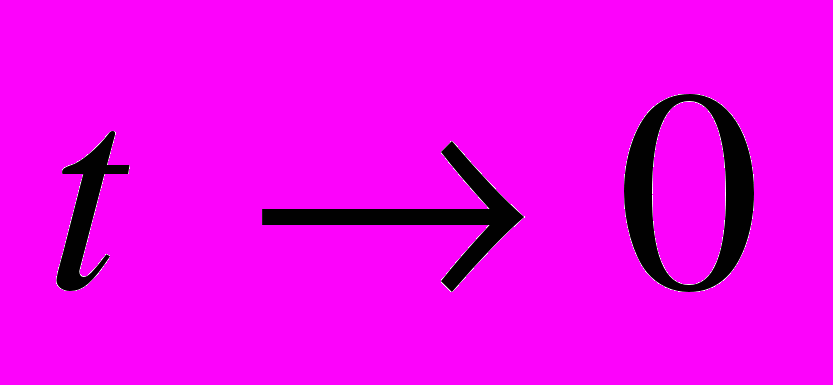