Програми для загальноосвітніх навчальних закладів Математика
| Вид материала | Документы |
- Атики в 5-9 класах загальноосвітніх навчальних закладів вивчатиметься за програмами,, 164.05kb.
- Особливості навчальної програми для учнів 8 класу загальноосвітніх навчальних закладів, 602.24kb.
- «Математика в школі», 894.13kb.
- «Математика в школі», 804.81kb.
- Програма для загальноосвітніх навчальних закладів (класів) з поглибленим вивченням, 717.77kb.
- Програми та рекомендації до розподілу програмного матеріалу загальноосвітніх навчальних, 2950.56kb.
- Програми та рекомендації до розподілу програмного матеріалу загальноосвітніх навчальних, 2719.13kb.
- Програми та рекомендації до розподілу програмного матеріалу загальноосвітніх навчальних, 1209.62kb.
- Програми та рекомендації до розподілу програмного матеріалу загальноосвітніх навчальних, 2778.79kb.
- Методичні рекомендації щодо викладання математики в 2010-2011 навчальному році, 805.17kb.
Програма з алгебри та початків аналізу
(2 год на тиждень, у І семестрі — 32 год, у II семестрі — 38 год, усього 70 год)
| № | Тема, мета вивчення, зміст навчального матеріалу | Основні вимоги до математичної підготовки учнів |
| І | Тригонометричні функції (16 год) | |
| | Мета. Повторити і розширити основні відомості про функції, набуті в основній школі. Ввести поняття тригонометричних функцій числового аргументу, навчити будувати графіки і розглянути основні властивості тригонометричних функцій. Ввести основні тригонометричні тотожності та навчити застосовувати їх до виконання тотожних перетворень. Числові функції. Зростаючі і спадні, парні і непарні функції. Побудова графіків функцій за допомогою геометричних перетворень. Тригонометричні функції кута. Радіанна міра кутів і дуг. Тригонометричні функції числового аргументу. Періодичність тригонометричних функцій. Властивості тригонометричних функцій. Побудова графіків тригонометричних функцій. Співвідношення між тригонометричними функціями одного аргументу. Тригонометричні тотожності: формули зведення, формули додавання, формули подвійного аргументу, [формули перетворення суми і різниці тригонометричних функцій у добуток, формули пониження степеня, формули перетворення добутку тригонометричних функцій у суму, формули половинного аргументу]. | Учні повинні: • мати уявлення — про радіанні міри кутів і дуг; — про тригонометричні функції числового аргументу 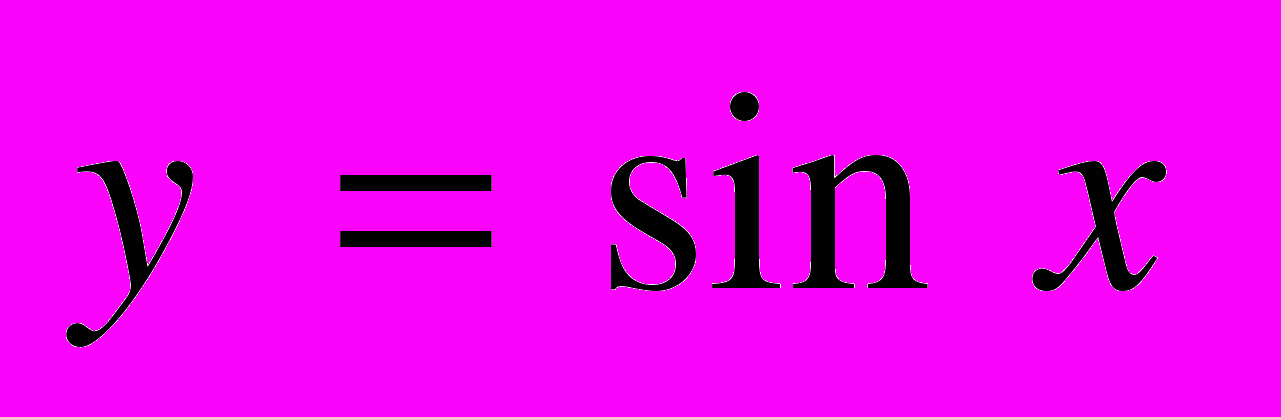 , , 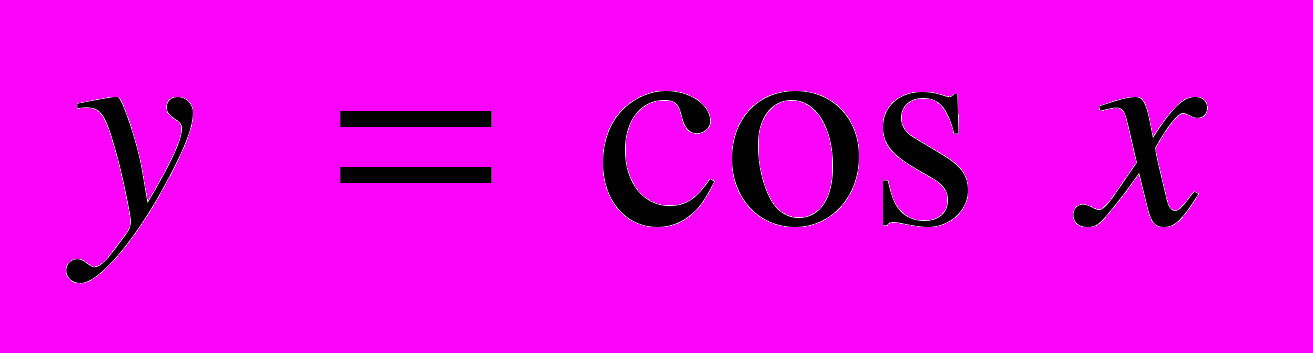 , , 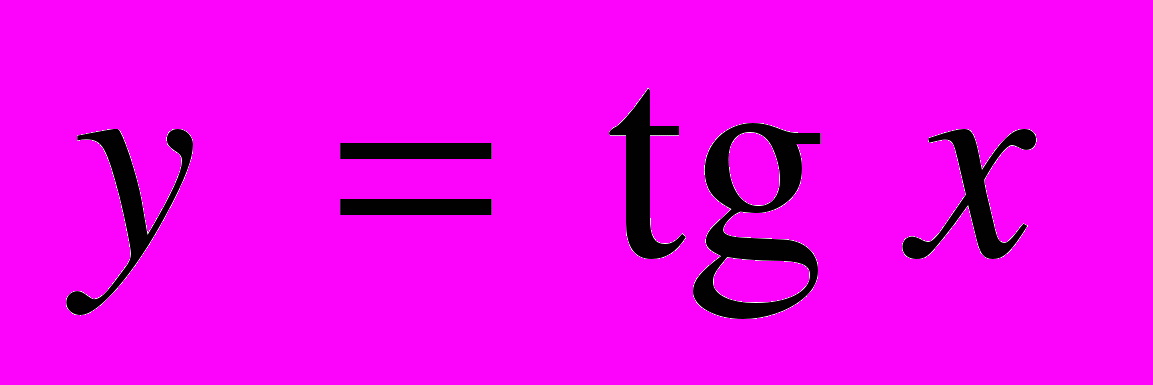 , , 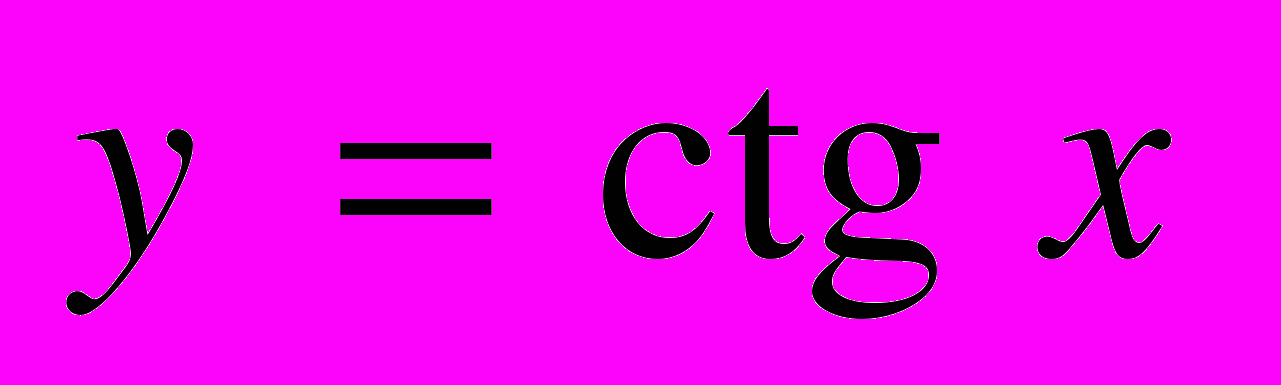 ; ;• знати — означення числової функції, зростаючої і спадної, парної і непарної, періодичної функції; — найменший додатний період і властивості кожної з тригонометричних функцій; — радіанні міри кутів 0°, 30°, 45°, 60°, 90°, 180°, 360°; — співвідношення між тригонометричними функціями одного аргументу; • вміти — доводити за означенням монотонність, парність, непарність вивчених раніше функцій; — переводити градусну міру в радіанну і навпаки; — будувати графіки тригонометричних функцій числового аргументу; — доводити співвідношення між тригонометричними функціями одного аргументу; — доводити тригонометричні тотожності та виконувати тотожні перетворення тригонометричних виразів. |
| ІІ | Тригонометричні рівняння нерівності (16 год) | |
| | Мета. Ввести поняття оберненої функції, обернених тригонометричних функцій; розглянути їх графіки і властивості. Ввести поняття тригонометричного рівняння і нерівності. Навчити розв’язувати найпростіші рівняння і нерівності та окремі види тригонометричних рівнянь, що зводяться до найпростіших. Обернена функція. Обернені тригонометричні функції [Їх графіки і властивості]. Розв’язування найпростіших тригонометричних рівнянь. Основні способи розв’язання рівнянь [та їх систем]. [Розв’язування найпростіших тригонометричних нерівностей]. | Учні повинні: • мати уявлення про — обернену функцію і обернені тригонометричні функції; — область визначення і область значень обернених тригонометричних функцій [і побудову їх графіків]; — тригонометричне рівняння і тригонометричну нерівність; • знати — формули загального розв’язку найпростіших тригонометричних рівнянь: 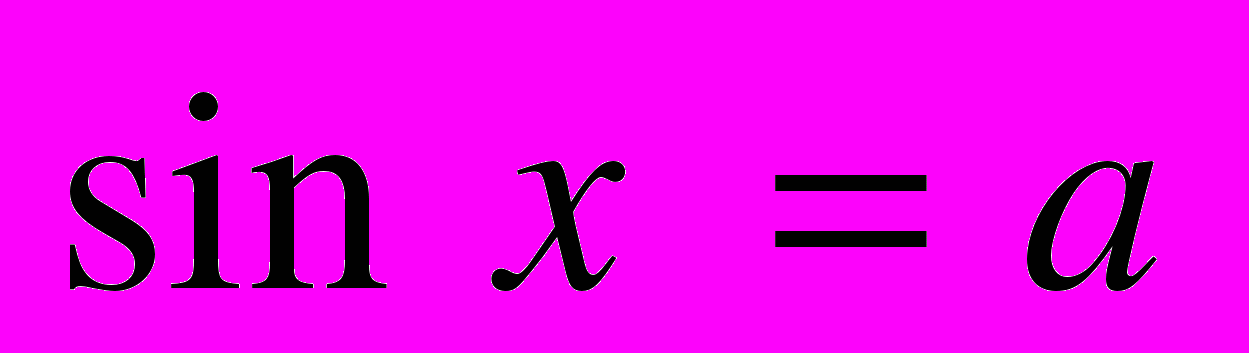 , , 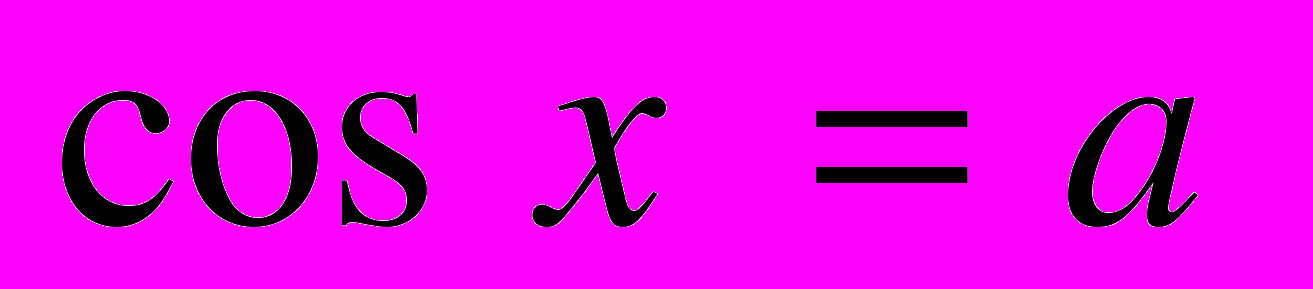 , , 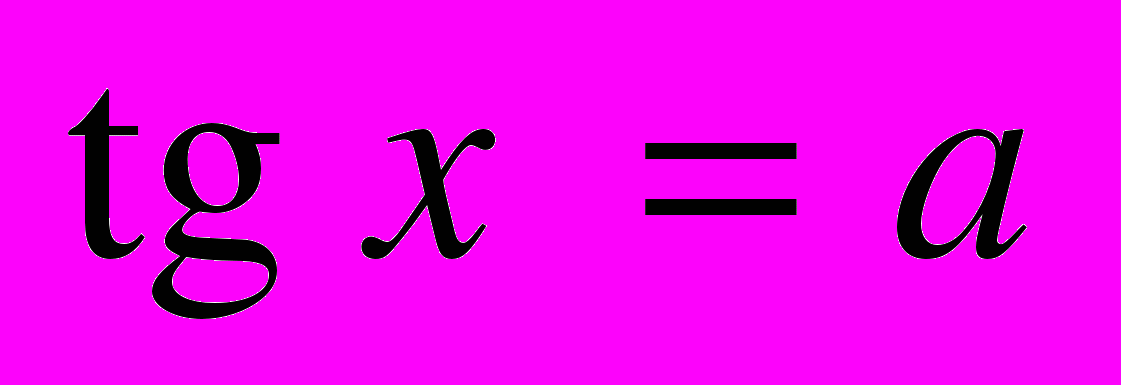 , , 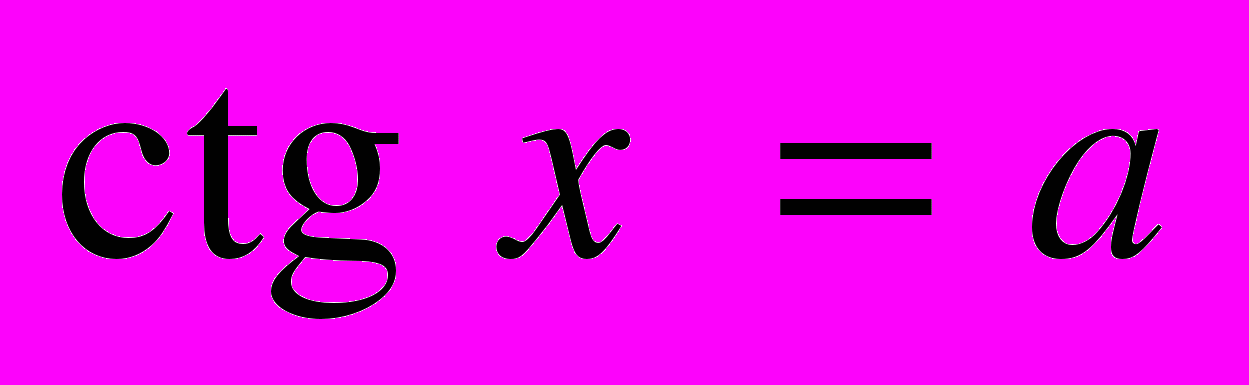 ; ;• вміти — розв’язувати тригонометричні рівняння і найпростіші тригонометричні нерівності. |
| ІІІ | Степенева функція (10 год) | |
| | Мета. Ввести означення кореня п-го степеня, арифметичного кореня п-го степеня; розглянути перетворення коренів та дії над коренями. Ввести означення ірраціонального рівняння [та нерівності]; навчити розв’язувати найпростіші ірраціональні рівняння [і нерівності]. Ввести поняття степеня з раціональним показником та розглянути його властивості. Ввести означення степеневої функції, розглянути її графік і властивості. Корінь п-го степеня. Арифметичний корінь п-го степеня та його властивості. Перетворення коренів. Дії над коренями. Ірраціональні рівняння [і нерівності]. [Система ірраціональних рівнянь]. Степінь з раціональним показником та його властивості. Узагальнення поняття степеня. Степенева функція, її графік і властивості. | Учні повинні: • мати уявлення про — ірраціональні рівняння [і нерівності]; — степінь з раціональним показником; • знати — означення кореня п-го степеня і арифметичного кореня п-го степеня; — властивості арифметичних коренів; — найпростіші перетворення коренів; — дії над коренями; — означення степеня з раціональним показником та його властивості; — означення степеневої функції, її графік і властивості; • вміти — виконувати основні перетворення коренів і дії над ними; — розв’язувати найпростіші ірраціональні рівняння [і нерівності]; — застосовувати властивості степеня з раціональним показником до перетворення виразів; — будувати ескізи графіків степеневих функцій і «читати» за графіками властивості функцій. |
| IV | Показникова і логарифмічна функції (20 год) | |
| | Мета. Ввести означення показникової і логарифмічної функцій, розглянути їх графіки і властивості. Розглянути способи розв’язування показникових рівнянь. нерівностей [та їх систем]. Ввести означення логарифма числа, довести основні логарифмічні тотожності та властивості логарифмів. Розглянути способи розв’язування логарифмічних рівнянь, нерівностей [та їх систем]. Показникова функція, її графік і властивості. Розв’язування показникових рівнянь, нерівностей [та їх систем]. Логарифм числа. Основна логарифмічна тотожність. Властивості логарифмів. Логарифмічна функція, її графік і властивості. Розв’язування логарифмічних рівнянь, нерівностей [та їх систем]. | Учні повинні: • знати — значення показникової функції, логарифма числа та логарифмічної функції; — основну логарифмічну тотожність і властивості логарифмів; — означення показникового і логарифмічного рівнянь, нерівностей; • вміти — будувати ескізи графіків показникової і логарифмічної функцій і «читати» за графіками властивості функцій; — спрощувати показникові та логарифмічні вирази, доводити найпростіші тотожності; — розв’язувати нескладні показникові і логарифмічні рівняння і нерівності. |
| V | Резерв навчального часу (8 год) | |
