Решение перечисленных задач требует применения методов, с помощью которых можно было бы провести оценку (расчёт) наиболее важных процессов, имеющих место в проектируемом изделии. Это достигается математическим моделированием

Вид материала

Подобный материал:

1 ... 14 15 16 17 18 19 20 21 ... 27

Подставляя численные значения, имеем: f⁽¹⁾ = [29 29 0 29 0 0]^T

Таким образом, результирующая система уравнений для первого конечного элемента примет вид: [K⁽¹⁾] {Ф} = {f⁽¹⁾}

½	1	-1	0		Ф₁	=	29
	-1	2	-1		Ф₂		29
	0	0	0		Ф₃		0	(13.40)
	0	-1	1		Ф₄		29	(13.40)
	0	0	0		Ф₅		0
	0	0	0		Ф₆		0

Системы уравнений для второго, третьего и четвертого элемента примут вид:

[K⁽²⁾] {Ф} = {f⁽²⁾}

½	0	0	0		Ф₁	=	0
	1	-1	0		Ф₂		29
	-1	2	-1		Ф₃		29	(13.40-а)
	0	0	0		Ф₄		0	(13.40-а)
	0	-1	1		Ф₅		29
	0	0	0		Ф₆		0

[K⁽³⁾] {Ф} = {f⁽³⁾}

½	0	0	0		Ф₁	=	0
	1	-1	0		Ф₂		29
	0	0	0		Ф₃		0	(13.40-б)
	-1	2	-1		Ф₄		29	(13.40-б)
	0	-1	1		Ф₅		29
	0	0	0		Ф₆		0

[K⁽⁴⁾] {Ф} = {f⁽⁴⁾}

½	0	0	0		Ф₁	=	0
	0	0	0		Ф₂		0
	0	0	0		Ф₃		0	(13.40-в)
	-1	-1	0		Ф₄		29	(13.40-в)
	-1	2	-1		Ф₅		29
	0	-1	1		Ф₆		29

Окончательная система уравнений примет вид: [K] {Ф} = {f}

½	1	-1	0	0	0	0		Ф₁	=	29
	-1	4	-1	-2	0	0		Ф₂		87
	0	-1	2	0	-1	0		Ф₃		29	(13.40-г)
	0	-2	0	4	-2	0		Ф₄		87	(13.40-г)
	0	0	-1	-2	4	-1		Ф₅		87
	0	0	0	0	-1	1		Ф₆		29

Величины Ф₃, Ф₅ и Ф₆ равны нулю, так как соответствующие им узлы расположены на внешней границе. Преобразуя и решая систему, получим:

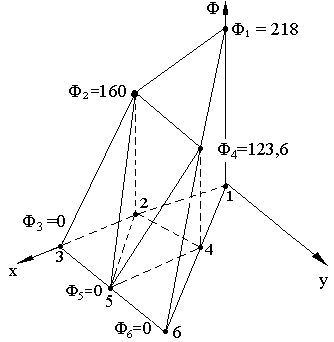
{Ф}^Т = {218 160 0 123,6 0 0}^Т

Представляет особый интерес поверхность , соответствующая полученному множеству узловых значений. Эта поверхность представлена на рисунке 13.10. Дело в том, что объем тела, ограниченный этой поверхностью, пропорционален не найденному пока моменту М, закручивающему стержень на один градус на длине 1 метр. Кроме того, не определены еще сдвиговые напряжения.

1. Вычисляем сдвиговые напряжения, связанные с найденной функцией напряжений формулами (13.27). Согласно выражениям (13.27) и (13.30), запишем выражение для матрицы–столбца сдвиговых напряжений первого элемента, выраженное через определенную уже матрицу градиентов (13.37):

					218
					160
 ⁽¹⁾ =	x	= [B⁽¹⁾]{Ф} =	-4 4 0 0 0 0		0	=	-232,6
 ⁽¹⁾ =		= [B⁽¹⁾]{Ф} =	0 –4 0 4 0 0		123,6	=	-145,4
	y				0
					0

_zy⁽¹⁾ = -		= 232,6(н/см²); _zy⁽¹⁾ =		= -145,4(н/см²);
	x		y

Компоненты тензора напряжений для других элементов вычислим аналогично:

_ZY⁽²⁾ =640,0(н/см²); _ZX⁽²⁾ =0,0(н/см²);

_ZY⁽³⁾ =494,0(н/см²); _ZX⁽³⁾ = -145,4(н/см²);

_ZY⁽⁴⁾ =494,0(н/см²); _ZX⁽⁴⁾ =0,0(н/см²);

Полученные компоненты тензора напряжений схематически показаны на рисунке. 13.11. Внутри каждого конечного элемента сдвиговые напряжения постоянны, так как интерполяционные полиномы взяты линейными по Оx и Оy.


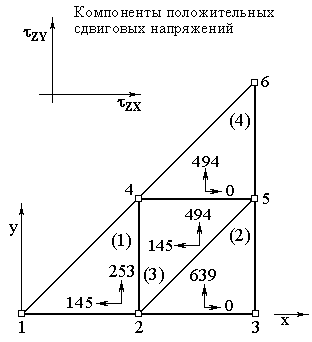Рис. 13.10	Рис. 13.11

2. Вычисляем момент, который согласно определению равен:

		М = 2		 dS
		М = 2	S

где: S – площадь поперечного сечения стержня.

Учитывая аддитивный характер момента, можно записать выражение для части момента, действующего в пределах рассматриваемого участка стержня:

		М_О=	М ^(е) =			2^(е)dА		(13.41)
			е	е	А^(е)

Поскольку площади всех четырех конечных элементов равны, обозначим:

А⁽¹⁾=А⁽²⁾=А⁽³⁾=А⁽⁴⁾=А

Величины ^(е)при известных функциях формы определяются по (13.29).

Для первого элемента имеем:

М ⁽¹⁾	= 2 	^(е)dА	= 2 	[N₁⁽¹⁾ N₂⁽¹⁾ 0 N₄⁽¹⁾ 0 0] {Ф}dA
	А		А

Откуда:

М ⁽¹⁾	= 2 {Ф}^Т	[N⁽¹⁾] ^Т dА
	А

Интеграл в полученном выражении идентичен вычисленному ранее интегралу (13.39). Поэтому можно сразу записать:

М ⁽¹⁾ =	2	А {Ф}^Т[ 1 1 0 1 0 0] =	2	А (Ф₁ + Ф₂ + Ф₄)
	3		3

Подставляя значения , найденные в узловых точках, имеем:

М ⁽¹⁾ = 0,67 А (218 + 160 +123,63) = 0,67 А (501,8)

Аналогично находим для остальных элементов:

М ⁽²⁾ =	0,67 А (Ф₂ + Ф₃ + Ф₅) = 0,67 А (160)

М ⁽³⁾ =	0,67 А (Ф₂ + Ф₅ + Ф₄) = 0,67 А (283,6)

М ⁽⁴⁾ =	0,67 А (Ф₄ + Ф₅ + Ф₆) = 0,67 А (123,6)

Суммируя эти соотношения по формуле (13.40), получим:

М_О= 0,67 А (501,8 + 160 + 283,6 + 123,6) = 0,67 А (1069)

Поскольку на элементы разбивалась только 1/8 часть поперечного сечения стержня и А=1/32, полный крутящий момент M составит:

М = 8 М_О = 8 (0,67)  (1/32)  (1069) = 178,16 (нсм)

Это означает, что крутящий момент величиной 178 Хнсм) вызовет закручивание на 1^о стального стержня длиной 1 м. Теоретическое значение связи между приложенным крутящим моментом и углом закручивания квадратного стержня со стороной, равной L (м), дается формулой:

М = 0,1406GL⁴ =0,1406810⁶[н/м²]1(рад/м)1(м)=196,3(нсм)

Полученное расхождение в 9,5% объясняется выбором грубой сетки разбиения.

13.4 Метод прямой жесткости

Применение метода конечных элементов, как показано на ряде примеров, приводит к системе алгебраических уравнений. Порядок системы уравнений совпадает с числом неизвестных узловых значений и может достигать сотен тысяч. Метод построения глобальной матрицы жесткости, рассмотренный в разделе 13.3, весьма неэффективен, если в таком виде пытаться реализовать его ЭВМ. Дело в том, что матрица жесткости отдельного конечного элемента [k⁽^e⁾] (назовем ее локальной матрицей жесткости – ЛМ), имеет такое же число строк и столбцов, что и глобальная матрица жесткости (ГМ) [K], однако, большинство коэффициентов ЛМ равно нулю. Действительно, на рисунке 13.12 показана область, разбитая на 16 элементов и имеющая 15 узловых точек. Матрица жесткости для первого элемента этой области, показанная на рисунке 13.13, содержит 15 х 15 = 225 коэффициентов. Видно, что только девять из них - ненулевые, что составляет 4% от общего числа ячеек, занимаемых в ОЗУ матрицей ЛМ.


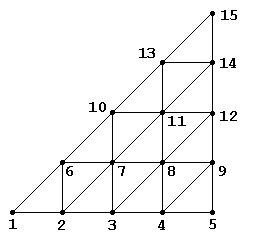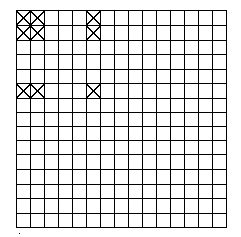Рис.13.12	Рис.13.13

С ростом числа узлов процент нулевых элементов резко увеличивается. Например, для 75 узлов он составляет (75 х 75 –9)/(75 х 75) 100% = 99,84%. Кроме того, матрица элемента [k⁽^e⁾] должна быть вычислена отдельно от глобальной матрицы [K] и затем прибавлена к последней. Это, в свою очередь, требует запоминания в ОЗУ обеих матриц: и [k⁽^e⁾] и [k⁽^e⁾].

В эффективных программах процедура построения ГМ использует сокращенную форму локальных матриц элементов [N⁽^e⁾] при получении уравнений для элементов. Такой метод известен как метод прямой жесткости (МПЖ).

Рассмотрим процедуру кодирования ЛМ в методе МПЖ. С этой целью перепишем систему интерполяционных полиномов (13.29), исключив из неё все глобальные степени свободы , не относящиеся к конкретному элементу:

⁽¹⁾ = N₁⁽¹⁾Ф₁ + N₂⁽¹⁾Ф₂ + N₄⁽¹⁾Ф₄

⁽²⁾ = N₂⁽²⁾Ф₂ + N₃⁽²⁾Ф₃ + N₅⁽²⁾Ф₅

⁽³⁾ = N₂⁽³⁾Ф₂ + N₄⁽³⁾Ф₄ + N₅⁽³⁾Ф₅

⁽⁴⁾ = N₄⁽⁴⁾Ф₄ + N₅⁽⁴⁾Ф₅ + N₆⁽⁴⁾Ф₆

(13.42)

Blog