Решение перечисленных задач требует применения методов, с помощью которых можно было бы провести оценку (расчёт) наиболее важных процессов, имеющих место в проектируемом изделии. Это достигается математическим моделированием
| Вид материала | Решение |
- Решение. Из анализа схемы следует, что резисторы, 80.22kb.
- Биохимия нервной ткани, 139.51kb.
- Как провести анализ урока, 130.36kb.
- Решение задач одно из важных применений Excel. Системы линейных уравнений решаются, 39.61kb.
- Контрольные вопросы по дисциплине " экономико- математические методы и модели", 19.66kb.
- Рабочая программа учебной дисциплины компьютерные технологии в науке Кафедра-разработчик, 180.63kb.
- Элективный курс «Компьютерное моделирование физических процессов с помощью математического, 342.03kb.
- Рабочая программа учебной дисциплины компьютерные технологии в науке и производстве, 153.39kb.
- Решение задач по стереометрии, 236.55kb.
- Сопровождение программы: доработка программы для решения конкретных задач, 167.56kb.
наконец, обозначая среднюю площадь элемента как Â =(Ai+Aj)/2, имеем:
| | KV(е) = | Â(е) | [ | 1 | -1 | ] | (12.23) |
| | L | -1 | 1 |
Формулы (12.23) = (12.6) с точностью замены площади ее средним значением.
Матрица KS(е) с учетом (12.9) примет вид:
| | | | [N]T[N] dS = | | L | | | |
| KS(е) = | h | | h | | Ni2 | Ni Nj | P(x)dx | |
| Ni Nj | Nj2 | |||||||
| | | S | | 0 | | | ||
Вычислим первый коэффициент, определяемый выражением:
| L | Ni2 P(x)dx = | L | (Ni3 Pi + Ni2 NjPj) dx = | | |
| | | L | (3 Pi +Pj) | ||
| 12 | |||||
| 0 | 0 | | |||
Вычисляя остальные коэффициенты, получим окончательное выражение для поверхностной составляющей матрицы теплопроводности элемента:
| KS(е) = | h L | (3 Pi +Pj) | (Pi +Pj) | (12.24) |
| 12 | (Pi +Pj) | (3 Pi +Pj) |
Сумма (12.23) и (12.24) и определит выражение для искомой матрицы теплопроводности рассматриваемого конечного элемента.
3. Составляем матрицу вектора сил элемента. Согласно формуле (12.11), матрица вектора сил примет вид:
| | | | [N]T dS = h TOC | L | | |
| FS(е) = | h TOC | | | Ni | (NiPi + NiNjPj)dx | |
| Nj | ||||||
| | | S | 0 | | ||
Откуда, перемножая матрицу-столбец на коэффициент, имеем:
| | h TOC | L | | |
| FS(е) = | | Ni(NiPi + NiNjPj) | dx | |
| Nj(NiPi + NiNjPj) | ||||
| | 0 | | ||
Вычислим интеграл для верхнего коэффициента матрицы-столбца:
| L | Ni2Pidx + | L | Ni NjPj dx = | | |||||||||||||
| | | Pi | (1 - | х | )3 | L | + | Pj х2 | | L | - | Pj х3 | | L | = | ||
| 3 | L | 0 | 2L2 | 0 | 3L3 | | 0 | ||||||||||
| 0 | 0 | | | | |||||||||||||
Подставляя пределы и записывая результат в матричном виде, получим:
-
=
Pi
+
Pj
=
1
[2 1] {
Pi
}
3
6
6
Pj
Вычисляя остальные коэффициенты, получим окончательное выражение для вектора нагрузки произвольного конического стержня:
| | | | [N]T dS = | | | | | | ||
| FS(е) = | h TOC | | hLTOC | 2 | 1 | { | Pi | } | (12.25) | |
| 6 | 1 | 2 | Pj | |||||||
| | | S | | | | | | |||
Пример 12.2. Вычислить распределение температур в стержне из примера 12.1, имеющего коническую форму, если температура большего по диаметру основания конуса постоянна и равна 150оС.
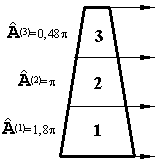 | X4 =7,5см ( R4=0,5; A4=0,25; P4 = ) X3 =5см ( R3=0,83; A3=0,71; P3=1,66 ) X2=2,5см ( R2=1,16; A2=1,35; P2=2,32 ) X1=0 ( R1=1,5; A1=2,25; P1=3 ) |
| Рис. 12.5 | |
Решение.
- Разбиваем стержень на три конечных элемента длиной по L=2,5см.
- Рассчитываем геометрические характеристики (Â(e), Рq, Аq, Rq, где q=1,…,4) – результаты расчета приведены на рисунке 12.5.
- Рассчитываем значения коэффициентов, входящих в выражения для матриц выделенных конечных элементов (12.23 – 12.25):
/L = 75[Вт/(смОС)]/2,5(см)=30(Вт/см2 ОС);
hL/12 = 10[Вт/(см2 ОС)]2,5(см)/12=2,1(Вт/см2 ОС);
hTocL/6 = 10[Вт/(см2 ОС)] 40ОС2,5(см)/6=166,7(Вт/см);
- Вычисляем согласно (12.23) объемную составляющую матрицы теплопроводности элементов:
| KV(1) = | 301,8 | 1 | -1 | = | 54 | -54 | | |
| -1 | 1 | -54 | 54 |
| KV(2) = | 301,0 | 1 | -1 | = | 30 | -30 | | |
| -1 | 1 | -30 | 30 |
| KV(3) = | 300,48 | 1 | -1 | = | 14,4 | -14,4 | | |
| -1 | 1 | -14,4 | 14,4 |
- Складывая полученные матрицы по методу прямой жесткости, получаем объемную матрицу теплопроводности всего стержня:
KV =
54
-54
0
0
-54
84
-30
0
0
-30
44,4
-14,4
0
0
-14,4
14,4
- В соответствии с выражением (12.24) вычисляем поверхностную матрицу теплопроводности элементов:
| KS(1) = | 2,1 | (9+2,32) | (5,32) | = | 23,8 | 11,2 | | |
| (5,32) | (9+2,32) | 11,2 | 21 |
| KS(2) = | 2,1 | 8,66 | 4 | = | 18,2 | 8,4 | | |
| 4 | 7,32 | 8,4 | 15,4 |
| KS(3) = | 2,1 | 6 | 2,66 | = | 12,6 | 5,6 | | |
| 2,66 | 4,66 | 5,6 | 9,8 |
- Складывая полученные матрицы по методу прямой жесткости, получаем поверхностную матрицу теплопроводности всего стержня:
KS(1) +KS(2) +KS(3) =
23,8
11,2
0
0
11,2
39,2
8,4
0
0
8,4
28,0
5,6
0
0
5,6
9,8
- К полученной матрице необходимо добавить поверхностный интеграл, взятый по площади А4,=0,25 (см2). Используя выражение (12.19), имеем:
| K(3)S=А4 = | 100,25 | 0 | 0 | = | 0 | 0 | | |
| 0 | 1 | 0 | 2,5 |
- Складывая все матрицы, приходим к общей матрице теплопроводности стержня:
| KV +KS(1) +KS(2) +KS(3) +K(3)S=А4 = | 77,8 | -42,8 | 0 | 0 |
| -42,8 | 123,2 | -21,6 | 0 | |
| 0 | -21,6 | 72,4 | -8,8 | |
| 0 | 0 | -8,8 | 26,7 |
10. По формуле (12.25) вычисляем вектор нагрузки для каждого элемента:
| FS(1) = 166,7 | 2 | 1 | { | 3 | }= 166,7 { | 6+2,32 | } = { | 1376 | } |
| 1 | 2 | 2,32 | 3+4,64 | 1273 |
| FS(2) = 166,7 | 2 | 1 | { | 2,32 | }= 166,7 { | 4,64+1,66 | }= { | 1050 | } |
| 1 | 2 | 1,66 | 2,32+3,32 | 940 |
| FS(3) = 166,7 | 2 | 1 | { | 1,66 | }= 166,7 { | 3,32+1,0 | }= { | 720 | } |
| 1 | 2 | 1,0 | 1,66+2,0 | 610 |
11. К полученной матрице необходимо добавить поверхностный интеграл, взятый по площади А4= 0,25 (см2). Чтобы воспользоваться выражением (12.21), вычислим произведение:
(hTOCА4) = 10[Вт/(см2 ОС)]40(oC)0,25(см2)= 100
| F(3)S=А4 = | 100 { | 0 | } | = | { | 0 | } |
| 1 | 100 |
12. Приходим к системе уравнений:
-
77,8
-42,8
0
0
T1
=
1376
-42,8
123,2
-21,6
0
T2
2323
0
-21,6
72,4
-8,8
T3
1660
0
0
-8,8
26,7
T4
710
13. Решать данную систему уравнений есть смысл только для того, чтобы проверить правильность ее получения. Действительно, поскольку она не содержит сведений о действительной нагрузке стержня, мы должны получить:
T1= T2 =T3 =T4=40оС
По условию температура T1= 150оС, следовательно, первое и второе уравнение системы должны быть преобразованы. В частности, первое уравнение: (77,8150 – 42,8 T2 = 1376) не должно зависеть от величины температуры T2 , что возможно в единственном случае, когда: (– 42,8T2 = 0). Эта цель достигается принудительным присвоением первому коэффициенту вектора сил системы уравнений, полученной в пункте 12, величины F1=(77,8150 =11670). Второе уравнение также нуждается в преобразовании: после подстановки в него значения T1=150 оно принимает вид:
(– 42,8150 + 123,2T2– 21,6T3 = 2323)
откуда: F2=(2323+42,8150)=8743.
14. Приходим к окончательной системе уравнений:
-
77,8
-42,8
0
0
150
=
11670
-42,8
123,2
-21,6
0
T2
8743
0
-21,6
72,4
-8,8
T3
1660
0
0
-8,8
26,7
T4
710
- Решением системы с точностью до десятых долей градуса является вектор:
