Решение перечисленных задач требует применения методов, с помощью которых можно было бы провести оценку (расчёт) наиболее важных процессов, имеющих место в проектируемом изделии. Это достигается математическим моделированием
| Вид материала | Решение |
- Решение. Из анализа схемы следует, что резисторы, 80.22kb.
- Биохимия нервной ткани, 139.51kb.
- Как провести анализ урока, 130.36kb.
- Решение задач одно из важных применений Excel. Системы линейных уравнений решаются, 39.61kb.
- Контрольные вопросы по дисциплине " экономико- математические методы и модели", 19.66kb.
- Рабочая программа учебной дисциплины компьютерные технологии в науке Кафедра-разработчик, 180.63kb.
- Элективный курс «Компьютерное моделирование физических процессов с помощью математического, 342.03kb.
- Рабочая программа учебной дисциплины компьютерные технологии в науке и производстве, 153.39kb.
- Решение задач по стереометрии, 236.55kb.
- Сопровождение программы: доработка программы для решения конкретных задач, 167.56kb.
Вычислим далее значение частной производной Т(е) по координате х:
| | | дT[e] | = | дNi [e] | Ti + | дNj [e] | Tj | (12.4) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| | дx | дx | дx | |||||||||||
| Введем обозначение: | Bi[e] = | дNi [e] | | |||||||||||
| дx | | |||||||||||||
| и запишем (12.4) в матричной форме: | дT[e] | = [B[e]]{T} | (12.5) | |||||||||||
| дx | ||||||||||||||
Это позволяет получить выражение для функционала (е) в матричной форме. Согласно (12.2), (12.3) и (12.5) имеем:
| [e] = | | | [B[e]]{T}[B[e]]{T}dV | + | | q [N[e]]{T} dS + | ||||
| 2 | ||||||||||
| | V[e] | | S1[e] | | | |||||
-
+
(
h
[N[e]] {T} [N[e]] {T} – hTOC[N[e]]{T} +
(TOC)2
)
dS
(12.6)
2
2
S2[e]
Для вычисления искомых производных, в соответствии с исходной формулой (12.1), покажем предварительно, что в матричном виде:
-
д( [B[e]] {T} [B[e]] {T} )
= 2 B i [e] [B[e]] {T}
(12.7)
дx
Действительно, левая часть приведенного тождества представляет собой искомую частную производную от квадрата частной производной Т(е) по Ti , представленную в матричной форме, которая по определению производной от сложной функции и с учетом (12.5) равна:
| д | ( | ( | дT[e] | )2 | ) | = 2 | | | д | ( | дT[e] | ) | = 2 Bi[e] ( Bi[e]Ti + Bj[e]Tj ) |
| дx | дT[e] | | дx | ||||||||||
| дTi | дx | дTi | |||||||||||
Откуда, переходя к матричной форме, получаем выражение (12.7).
Итак, мы подготовили все необходимое для вычисления и представления в матричной форме искомой системы уравнений (12.1). Вычисления проведем в два этапа: на первом получим матрицы для конечных элементов, а на втором – объединим их в матрицы ИТО.
Первый этап состоит в вычислении частных производных от элементарного функционала [e] (12.7) по всем узловым значениям температуры. Последовательно находим для конечного элемента 1.
-
д[e]
=
B1[e][B[e]]{T}dV
+
q N1[e] dS +
дT1
V[e]
S1[e]
-
+
hN1[e][N[e]] {T} dS -
– hTOCN1[e] dS
(12.6)
S2[e]
S2[e]
Вектор {T} не зависит от переменных интегрирования, поэтому, объединяя первое и третье слагаемое, вынося этот вектор за скобки и вычисляя производные для остальных узловых переменных конечного элемента 1, приходим к системе:
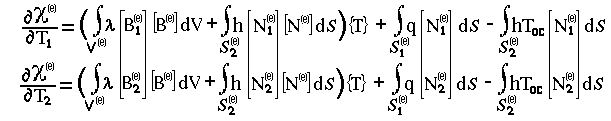 |
В данной системе выделены элементы, представляющие собой транспонированные матрицы [В(е)]T и [N(e)]T. Такое выделение позволяет записать вклад отдельного конечного элемента в общую сумму (12.1) в более общем матричном виде:
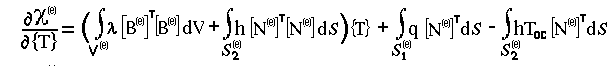 |
Введем обозначения:
-
KV[e] =
[B[e]]T [B[e]]dV
(12.8)
V[e]
-
KS[e] =
h [N[e]]T [N[e]]dS
(12.9)
S2 [e]
-
FS1[e] =
q [N[e]]T dS
(12.10)
S1[e]
-
FS2[e] =
h TOC[N[e]]T dS
(12.11)
S2 [e]
и запишем в матричной форме соотношение, представляющее вклад отдельного конечного элемента в общую сумму (12.1):
| д[e] | = ( [KV[e] ] + [KS[e] ] ) {T} + {FS1(e)} + {FS2(e)} = [K[e] ] {T} + {F(e)} | (12.12) |
| дT |
Здесь матрица теплопроводности конечного элемента[ K(e)] и его вектор нагрузки { F(e)} называются далее матрицами е-го конечного элемента. Приравнивая данное выражение нулю, запишем окончательную систему уравнений в краткой форме:
| [ K ] { T } = { F } | (12.13) |
где:
-
Е
[K] =
е=1
[K[e]]
(12.14)
и:
-
Е
[F] = -
е=1
{F[e]}
(12.15)
Рассмотрим методику получения матриц конечных элементов на нескольких примерах решения задачи переноса тепла в стержне.
Пример 12.1. Одномерный случай переноса тепла
Требуется вычислить температуру TХ на правом конце стержня, если температура его левого конца поддерживается равной величине T1=150оС. Радиус стержня R=1(см), длина L=7,5 (см). Коэффициенты теплопроводности материала стержня и конвективного теплообмена по всей поверхности стержня соответственно равны: =75 Вт/(см ОС), h = 10 Вт/(см2 ОС). Температура окружающей среды равна ТОС=40 ОС.
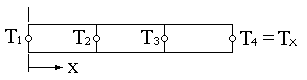 | 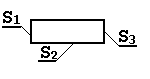 |
| Рис. 12.1 | Рис.12.2 |
