Решение перечисленных задач требует применения методов, с помощью которых можно было бы провести оценку (расчёт) наиболее важных процессов, имеющих место в проектируемом изделии. Это достигается математическим моделированием

Вид материала

Решение

Содержание For i:=1 to n do If defX[i]=1 Then UppCase(i) Метод конечных элементов (МКЭ) Симплекс - элементам Комплекс – элементам Функции формы.

Подобный материал:

• Решение. Из анализа схемы следует, что резисторы, 80.22kb.
• Биохимия нервной ткани, 139.51kb.
• Как провести анализ урока, 130.36kb.
• Решение задач одно из важных применений Excel. Системы линейных уравнений решаются, 39.61kb.
• Контрольные вопросы по дисциплине " экономико- математические методы и модели", 19.66kb.
• Рабочая программа учебной дисциплины компьютерные технологии в науке Кафедра-разработчик, 180.63kb.
• Элективный курс «Компьютерное моделирование физических процессов с помощью математического, 342.03kb.
• Рабочая программа учебной дисциплины компьютерные технологии в науке и производстве, 153.39kb.
• Решение задач по стереометрии, 236.55kb.
• Сопровождение программы: доработка программы для решения конкретных задач, 167.56kb.

Здесь, согласно условию задачи, фиксирована одна степень свободы узлового параметра {Т₁=150}. Преобразование системы проводим по шагам:

• коэффициенты 1-й строки, кроме диагонального коэффициента, равного К₁₁=46.6, приравниваем нулю:
  
• 46,6T₁ + 0 + 0 + 0 = 1000
  
• свободный член в 1-й строке заменяем произведением: (К₁₁Т₁)=6990:
  
• 46,6T₁ + 0 + 0 + 0 = 6990
  
• переменная Т₁ входит еще во второе уравнение, поэтому вычитаем из левой и правой части 2-го уравнения произведение К₂₁Т₁=(-21,7150):
  

0 + 93,2T₂ – 21,7T₃ + 0 = 2000–(-3255)= 5255

Таким образом, искомая система для решения примет вид:

46,6T₁ + 0 + 0 + 0 = 6990

0 + 93,2T₂ – 21,7T₃ + 0 = 5255

0 - 21,7T₂ + 93,2T₃ – 21,7T₄ = 2000

0 + 0 – 21,7T₃ + 56,6T₄ = 1400

что совпадает с системой из раздела 12.

В программе решения системы уравнений, приводимой на стр.27, преобразование выполняется оператором:

For i:=1 to n do If defX[i]=1 Then UppCase(i);

Собственно преобразование выполняется подпрограммой UppCase, которая в качестве параметра принимает номер фиксированной степени свободы. Последний выбирается из исходного линейного массива defX, в котором каждый фиксированный параметр должен быть заранее помечен единицей. Учебная pascal-программа преобразования и решения системы из n ЛАУ приведена в приложении:

5. Метод конечных элементов (МКЭ)

5.1. Типы конечных элементов.

Используемые в настоящее время численные методы рассматривают ДУ непосредственно в той форме, в которой в которой они были выведены (без каких-либо дальнейших математических преобразований и манипуляций) при помощи: (а) аппроксимации дифференциальных операторов конечно-разностными алгебраическими операторами, действующими в последовательности узлов, находящихся в области; (б) при помощи представления самой области элементами среды, не являющимися бесконечно малыми (то есть конечными элементами), которые в совокупности аппроксимируют реальную систему. Наиболее громоздкой и трудно программируемой операцией в МКЭ является учет граничных условий задачи, причем точность полученного численного решения полностью зависит от степени измельченности сетки, определяющей узловые точки. Отсюда следует, что в процессе решения задачи программисту приходится иметь дело с системами алгебраических уравнений очень высокого порядка.

В настоящее время наиболее популярным является второй подход, состоящий в возврате к характерному для физики разбиению ИТО на элементы конечных размеров, причем, чем больше по размерам эти элементы, тем лучше для минимизации числа получаемых уравнений. Поведение каждого элемента приближенно воспроизводит поведение малой области ИТО, которую он представляет. Однако условие полной непрерывности между элементами налагается только в узлах, а не на всем протяжении границ раздела. Диапазон применимости МКЭ, его высокая эффективность и сравнительная простота, с которой могут быть учтены реальные граничные условия, делают МКЭ серьезным соперником для любого конкурирующего метода.

К недостаткам метода следует отнести: (а) в основе МКЭ лежит дискретизация всего ИТО, что неизбежно ведет к очень большому количеству конечных элементов (особенно в трехмерных задачах); (б) МКЭ часто приводит к нереальным разрывам значений физических величин между смежными элементами.

При решении задач методом КЭ используются одномерные, 2 и 3-мерные КЭ. Одномерный КЭ показан на рисунке 9.1. Площадь поперечного сечения одномерного КЭ может изменяться по длине, но в большинстве практических задач ее считают постоянной. Наиболее часто такой элемент используется в одномерных задачах распространения тепла и в задачах строительной механики.

Рис. 9.1

Для построения дискретной модели двумерной области используют треугольники и 4-хугольники, которые могут иметь как прямолинейные, так и криволинейные стороны.

Собственно процесс дискретизации ИТО может быть разделен на два этапа: (а) разбиение ИТО на КЭ и (б) нумерация элементов и узлов. Последний этап может существенно повлиять на эффективность вычислений.

Требование простоты КЭ связано с тем, что при моделировании области должно быть использовано большое число элементов, поэтому деление области на треугольники является наилучшим способом разбиения.

МКЭ основан на аппроксимации непрерывной функции (температура, давление, перемещение и др.) дискретной моделью, которая строится на множестве кусочно-непрерывных функций, определенных на конечном числе подобластей, называемых элементами. В качестве функции, действующей внутри границ (и на границах) элемента обычно применяется полином, порядок которого и определяет тип элемента.

На практике используются три типа элементов: симплекс-элемент, комплекс-элемент и мультиплекс-элемент.

Симплекс - элементам соответствуют полиномы, содержащие константу и линейные члены. Число коэффициентов в таком полиноме на 1 больше размерности координатного пространства. Например, полином:  = ₁ +₂ x +₃ y представляет собой симплексную функцию для двумерного треугольного элемента. Этот полином линеен по X и Y и содержит три коэффициента, потому что треугольник имеет три узла.

Комплекс – элементам соответствуют полиномиальные функции, содержащие константу, линейные члены, а также члены второго, третьего и более высоких порядков, если это необходимо. Форма комплекс – элементов может быть такой же как у симплекс - элементов, но с дополнительными граничными (и даже внутренними) узлами. Число узлов в комплекс – элементе должно быть больше размерности координатного пространства + 1. Интерполяционный полином для 2-мерного треугольного комплекс – элемента имеет вид:

 = ₁ + ₂x + ₃y + ₄x² + ₅ xy + ₆y² (9.2)

Это соотношение включает шесть коэффициентов, поэтому рассматриваемый элемент должен иметь шесть узлов.

Для мультиплекс – элементов также используются полиномы, содержащие члены высокого порядка, Однако, для обеспечения непрерывности при переходе от одного мультиплекс – элемента к другому границы элементов должны быть параллельны осям координат. Примером мультиплекс – элемента является прямоугольный элемент.

5.2 . Функции формы.

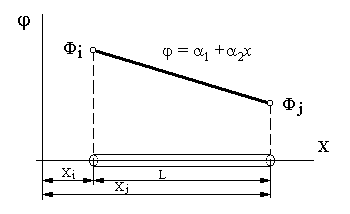Рис. 9.2

Одномерный симплекс – элемент представляет собой прямолинейный отрезок длины L с двумя узлами – по одному на каждом конце отрезка (рисунок 9.2). Узлы обозначаются индексами i и j, значения функции в узлах – через Фi и Фj соответственно. Начало системы координат располагается вне КЭ. Полиномиальная функция  для скалярной величины (например, температуры – Т или давления – Р) такова:

 = ₁ +₂ x (9.3)

Коэффициенты ₁ и ₂ определяются с помощью условий в узловых точках:

 = Ф_i при x = X_i и  = Ф_j при x = X_j.

Эти узловые условия приводят к системе двух уравнений:

Ф_i = ₁ +₂ X_i Ф_j = ₁ +₂

решение которой дает: ₁= (Ф_i X_j - Ф_j X_i)/L; ₂ = (Ф_j - Ф_i )/L

Подставляя найденные значения ₁ и ₂ в формулу (9.3), получим:

 = (Ф_iX_j-Ф_jX_i)/L +{(Ф_j-Ф_i)/L}x

Данное уравнение может быть переписано в виде:

 = [(X_j-x)/L]Ф_i+[(x-X_i)/L]Ф_j (9.4)

Линейные функции от х в формуле (9.5) называются функциями формы (ФФ) или интерполяционными функциями. Далее эти функции обозначаются через N. Каждая ФФ должна быть снабжена нижним индексом для обозначения узла, к которому она относится. Произвольную ФФ будем обозначать через N_. В формулу (8.5) входят следующие ФФ:

Ni =	Xj-x	;	и	Nj =	x-Xi
	L				L

Используя эти ФФ, запишем выражение (9.5) в матричной форме:

 = NiФi + NjФj = [N]{Ф} = [Ni Nj]	Фi	= [Ni Nj] [Фi Фj]Т	(9.6)
	Фj

Функция Ni = 1 в узле с номером i и равна нулю в j-м узле. Аналогично функция Nj = 1 в узле с номером j и равна нулю в i-м узле. Эти значения характерны для функций формы. Они равны 1 в одном определенном узле и обращаются в 0 в остальных узлах.

Пример 9.1. Одномерный симплекс-элемент используется для аппроксимации температуры в стержне. Узлы 1 и 2 имеют координаты 1,5 и 6 см соответственно. Известно, что температура в узлах 1 и 2 равна 120 и 90 градусов соответственно. Требуется определить температуру в точке х = 4 см и градиент температуры внутри элемента.

Решение: Пользуясь выражением (9.5) для одномерного симплекс – элемента, можно записать закон изменения температуры внутри КЭ:

t =	(Xj-x)	Ti +	(x-Xi)	Tj
	L		L

Данные КЭ: Xi=1,5 см; Ti=120^oC; X j=6,0 см;

Tj=90^oC; x=4 см; L = (Xj – Xj ) = 4,5 см.

Подставляя данные в формулу для температуры получаем:

t =	(1,5 - 4)	120o +	(4 – 1,5)	90o = 103,33 oC
	4,5		4,5

Для градиента температуры имеем:

dt	= -	Ti	+	Tj	= -	120o	+	90o	= -6,67 oC/см
dx		L		L		4,5		4,5

Двумерный симплекс – элемент показан на рисунке 9.3 – это треугольник с прямолинейными сторонами и тремя узлами, по одному в каждой вершине. Примем последовательную логическую нумерацию узлов элемента против часовой стрелки, начиная от произвольно выбранного i-го узла. Узловые значения скалярной величины  обозначим через Фi, Фj, Фk, а координатные пары трех узлов - через (Xi, Yi), (Xj, Yj), (Xk, Yk).

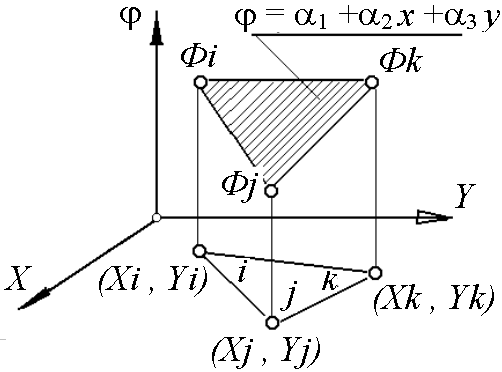
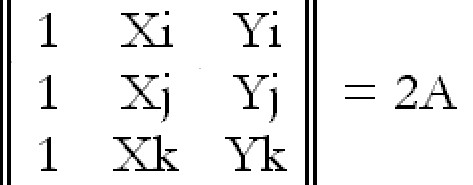
Рис. 5.3	Рис. 5.4

Интерполяционный полином в данном случае примет вид:

 = ₁ +₂ x +₃ y (5.7)

В узлах выполняются следующие условия:  = Фi при x = Xi и y = Yi

 = Фj при x = Xj и y = Yj  = Фk при x = Xk и y = Yk

Подстановка их в (9.7) приводят к системе трех уравнений:


Фi = 1 + 2 Xi + 3 Yi

Ф j = 1 + 2 Xj + 3 Yj (9.8)

Фk = 1 + 2 Xk + 3 Yk

Обозначим площадь симплекс – треугольника буквой А. Можно показать, что определитель системы (9.8) связан с А (рис. 5.4) соотношением:

[XjYk – XkYj + XiYj – XiYk + XkYi – XjYi] =2A


Решая систему (9.8) с учетом (9.8) и вводя обозначения:

Ai=(Xj Yk – Xk Yj); Bi=(Yj – Yk); Ci=(Xk – Xj),

Aj = (Xk Yi – Xi Yk), Bj = (Yk – Yi), Cj =(Xi – Xk), (9.9)

Ak =(Xi Yj – Xj Yi), Bk = (Yi – Yj), Ck = (Xj – Xi),

получим значения искомых коэффициентов:

1 = 0,5 А ^–1 [ Ai Фi + Aj Фj + Ak Фk ]

2 = 0,5 А ^–1 [ Bi Фi + Bj Фj + Bk Фk ]

3 = 0,5 А ^–1 [ Ci Фi + Cj Фj + Ck Фk ]

Подставляя значения 1, 2, 3 в (9.7) и преобразуя получаемые выражения к виду, подобному (9.6), получим выражение для скалярной величины :

 = Ni Фi + Nj Фj + Nk Фk (9.10)

где:

Ni =	Ai+Bix+Ciy	; Nj =	Aj+Bjx+Cjy	; Nk =	Ak+Bkx+Cky	(9.11)
	2A		2A		2A

Значение Ni в i-м узле составит: Ni = 0,5 А ^–1 [Ai + Bi x + Ci y] =

= 0,5 А ^–1 [Xj Yk – Xk Yj + (Yj – Yk) Xi + (Xk – Xj) Yi] =

= 0,5 А ^–1 [XjYk – XkYj + XiYj – XiYk + XkYi – XjYi] = 1

Непосредственной проверкой можно показать, что в остальных узлах Ni = 0.

Из (9.11) видно, что ФФ линейны по x и y, то есть, градиенты этой величины в направлениях Ox и Oy будут постоянны. Заметим, что:

	дN	= В	( = j, j, k)
	дx

поэтому градиент  в направлении оси Ох составит:

дФ	=	дNi	Фi +	дNi	Фj +	дNk	Фk =	BiФi + BjФj + BkФk	(9.12)
дx		дx		дx		дx