Решение перечисленных задач требует применения методов, с помощью которых можно было бы провести оценку (расчёт) наиболее важных процессов, имеющих место в проектируемом изделии. Это достигается математическим моделированием

Вид материала

Решение

Подобный материал:

• Решение. Из анализа схемы следует, что резисторы, 80.22kb.
• Биохимия нервной ткани, 139.51kb.
• Как провести анализ урока, 130.36kb.
• Решение задач одно из важных применений Excel. Системы линейных уравнений решаются, 39.61kb.
• Контрольные вопросы по дисциплине " экономико- математические методы и модели", 19.66kb.
• Рабочая программа учебной дисциплины компьютерные технологии в науке Кафедра-разработчик, 180.63kb.
• Элективный курс «Компьютерное моделирование физических процессов с помощью математического, 342.03kb.
• Рабочая программа учебной дисциплины компьютерные технологии в науке и производстве, 153.39kb.
• Решение задач по стереометрии, 236.55kb.
• Сопровождение программы: доработка программы для решения конкретных задач, 167.56kb.

Здесь через x обозначено несуществующее число (обычно в ЭВМ оно заменяется нулем при начальной чистке). При этом первая строка соответствует членам главной диагонали, а второй заполнен коэффициентами диагонали, следующей за главной диагональю.

При использовании одномерного массива в его начало помещаются искомые узловые значения {Т}, затем следует глобальный вектор нагрузки {F} и далее строка за строкой следует матрица жесткости в виде (14.4) . Таким образом, в ОЗУ система (14.3) будет помещена в следующем порядке:

T1	T2	T3	T4	1000	2000	2000	1400	47	93	93	57	-22	-22	-22	x
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16

В нижней строке приведены адреса ячеек ОЗУ. Порядковые номера расположения первых коэффициентов {T} являются указателями, пользуясь которыми возможно программное восстановление любого уравнения и его части для обработки в процессе решения системы. Пусть, например, необходимо восстановить (для просмотра) третье уравнение системы из n=4 уравнений, пользуясь ее машинным представлением. В данном случае три – индекс (i=3), по которому в ОЗУ храниться третья компонента вектора решения (T₃). Далее, по индексу (n + i)=(4+3)=7 в ОЗУ расположен третий элемент вектора нагрузки (2000). Ширина полосы равна двум, поэтому индексы I_p(k) коэффициентов (k) искомого уравнения, отмеченных в (14.3) квадратами, примут вид: I₂(-27)=(3n+i-1)=12+3-1=14; I₃(93)=(2n+i)=8+3=11, I₄(-27)=(3n+i)=12+3=15. Индекс p соответствует номеру переменной. Те же формулы позволяют восстановить второе уравнение системы (i=2). Действительно, адрес верхнего подчеркнутого коэффициента (–27) равен I₁(-27)=(3n+i-1)=12+2-1=13; I₂(93)=(2n+i)=8+2=10, I₃(-27)=(3n+i)=12+2=14.

В качестве второго, более общего примера можно рассмотреть размещение в ОЗУ системы уравнений из задачи кручения стержня (13.40-г). Матрица жесткости системы имеет ширину, равную четырем, поэтому:

Ф1	Ф2	Ф3	Ф4	Ф5	Ф6	29	87	29	87	87	29
1	2	3	4	5	6	7	8	9	10	11	12

1	-1	0	0	4	-1	-2	0	2	0	-1	0
13	14	15	16	17	18	19	20	21	22	23	24

4	-2	0	х	4	-1	х	х	1	х	х	х
25	26	27	28	29	30	31	32	33	34	35	36

15. Метод сопряженной аппроксимации

Уточнить значения сдвиговых напряжений внутри стержня, полученные для каждого конечного элемента, позволяет теория сопряженной аппроксимации.

Пусть требуется уточнить значение сдвиговых напряжений _ZY в узлах сечения стержня. Искомые узловые значения обозначим вектором:

{}^T = {₁, ₂ , … , ₆} (15.1)

Для вычисления _i в соответствии с методом сопряженной аппроксимации необходимо решить следующую систему уравнений:

[C] {} = {R} (15.2)

В системе (15.2) матрицы [C] и {R} представляют собой сумму (по методу прямой жесткости) матриц элементов вида:

[C ^(e)] = _V [N ^(e)]^T [N ^(e)]dV (15.3)

[R ^(e)] = _V _ZY ^(e)[N ^(e)]^T dV (15.4)

В выражении (15.4) _ZY ^(e) представляют следующие, определенные ранее, сдвиговые напряжения для каждого конечного элемента:

{_ZY ^(e)}^T = {233, 639 , 494 , 494} [Н/см²] (15.5)

Поскольку внутри конечного элемента эти величины не изменяются, их можно вынести за знак интеграла. Само интегрирование в (15.4) может быть выполнено через L – координаты. Вспоминая выражение (13.39) и интегральную формулу (13.38), имеем для первого элемента:

						N1(1)
						N2(1)
			R(1) =		ZY (e)	0	dV		(15.6)
						N4(1)
				V		0
						0

Заменяя ФФ L – координатами:

L₁=N₁ ⁽¹⁾,L₂=N₂ ⁽¹⁾, L₃=N₄ ⁽¹⁾, (15.7)

имеем:

			R(1) =	А(1) ZY (e)	[ 1 1 0 1 0 0 ]T
				3

Подставляя численные значения, имеем: R⁽¹⁾ = А⁽¹⁾ [78 78 0 78 0 0]^T

Аналогичные вычисления для остальных конечных элементов приводят к следующим результатам:

R⁽²⁾ = А⁽²⁾ [0 213 213 0 213 0]^T

R⁽³⁾ = А⁽³⁾ [0 165 0 165 165 0]^T

R⁽⁴⁾ = А⁽⁴⁾ [0 0 0 165 165 165]^T

Объединяя матрицы по методу прямой жесткости и принимая А = А⁽¹⁾ = А⁽²⁾ = А⁽³⁾ = А⁽⁴⁾ =получим выражение для столбца свободных членов в (15.2):

R = А [78 456 213 408 543 165]^T

Для получения матрицы [C⁽¹⁾] выразим ФФ первого конечного элемента через L – координаты и воспользуемся выражением (15.7):

N⁽¹⁾ = [N₁⁽¹⁾ N₂⁽¹⁾ 0 N₄⁽¹⁾ 0 0] = [L₁ L₂ 0 L₃ 0 0]

Тогда произведение матриц в выражении (15.3) примет вид:

[N⁽¹⁾]^T[N⁽¹⁾] = [L₁ L₂ 0 L₃ 0 0]^T [L₁ L₂ 0 L₃ 0 0]=

				L12	L1 L2	0	L1 L3	0	0
				L1 L2	L22	0	L2 L3	0	0
			=	0	0	0	0	0	0
				L1 L3	L2 L3	0	L32	0	0
				0	0	0	0	0	0
				0	0	0	0	0	0

Запишем интегральную формулу для элемента а₁₁ полученной матрицы:

		S	L12 dS =	2A(1) 2!	=	A(1)	[ 2 ]
				(2+2)!		12

Аналогично вычислим интеграл для элемента а₁₂:

		S	L1L2 dS =	2A(1) 1! 1! 0!	=	A(1)	[ 1 ]
				(1+1+2)!		12

Вычисляя аналогично остальные интегралы, получаем матрицу [C⁽¹⁾]:

		2	1	0	1	0	0
		1	2	0	1	0	0
[C(1)] =	A(1)	0	0	0	0	0	0
	12	1	1	0	2	0	0
		0	0	0	0	0	0
		0	0	0	0	0	0

Таким образом, приходим к следующей системе уравнений:

		2	1	0	1	0	0		1	=	78
		1	2	0	1	0	0		2		456
	1	0	0	0	0	0	0		3		213
	12	1	1	0	2	0	0		4		408
		0	0	0	0	0	0		5		543
		0	0	0	0	0	0		6		165

Решение дает следующий результат: { } _ZY ^T = [71 437 724 354 671 476]^T.

Рассмотрим еще один пример, иллюстрирующий применение метода сопряженной аппроксимации.

Пример 15.1. Стальной конический стержень, показанный на рисунке 13.3-а, имеет длину 90 см и площадь поперечного сечения: у широкого закрепленного в стене основания S=12см², у свободного узкого торца 6 см². Стержень подвержен двум видам нагружения: а) в осевом направлении силой F=42 кН, приложенной с узкому торцу, и б) воздействию температуры t=40^oC, действующей равномерно по всей длине.

Требуется определить значение напряжений в основаниях стержня и в точках А и В, делящих стержень на 3 равные части, если Т_ОС=20⁰C, а температурный коэффициент расширения материала стержня равен: ТКС=710^–6 [⁰C]^–1

Решение.

Разбиваем стержень на три конечных элемента по L=30 см. Задачу решаем в два этапа: на первом вычисляем перемещения в узлах, а на втором – вычисляем напряжения в элементах и методом сопряженной аппроксимации находим значения напряжений в заданных точках.
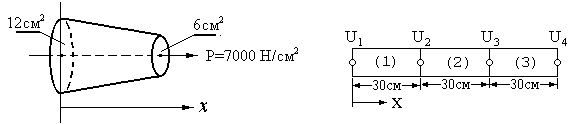