Решение перечисленных задач требует применения методов, с помощью которых можно было бы провести оценку (расчёт) наиболее важных процессов, имеющих место в проектируемом изделии. Это достигается математическим моделированием

Вид материала

Решение

Подобный материал:

• Решение. Из анализа схемы следует, что резисторы, 80.22kb.
• Биохимия нервной ткани, 139.51kb.
• Как провести анализ урока, 130.36kb.
• Решение задач одно из важных применений Excel. Системы линейных уравнений решаются, 39.61kb.
• Контрольные вопросы по дисциплине " экономико- математические методы и модели", 19.66kb.
• Рабочая программа учебной дисциплины компьютерные технологии в науке Кафедра-разработчик, 180.63kb.
• Элективный курс «Компьютерное моделирование физических процессов с помощью математического, 342.03kb.
• Рабочая программа учебной дисциплины компьютерные технологии в науке и производстве, 153.39kb.
• Решение задач по стереометрии, 236.55kb.
• Сопровождение программы: доработка программы для решения конкретных задач, 167.56kb.

4) Глобальная система после добавления сюда локальных матриц для четвертого последнего конечного элемента приобретает окончательный вид:

½	1	-1	0	0	0	0		Ф1	=	29
	-1	4	-1	-2	0	0		Ф2		87
	0	-1	2	0	-1	0		Ф3		29
	0	-2	0	4	-2	0		Ф4		87
	0	0	-1	-2	4	-1		Ф5		87
	0	0	0	0	-1	1		Ф6		29

Как и следовало ожидать, мы получили ту же самую систему (13.40-г).

13.5 Задача изгиба опертой балки

Задача изгиба опертой балки с точки зрения метода конечных элементов представляет частный случай рассмотренной выше задачи о кручении бруса.

Условие задачи. Балка длиной L=150см, закрепленная по обоим концам, подвержена действию постоянного изгибающего момента М=6,7510⁵(Нсм). Точки А, В и С делят балку на 4 равные части. Прогиб балки Y(x) описывается дифференциальным уравнением вида (13.43). Требуется определить прогибы балки в точках А, В и С, если ее изгибная жесткость равна:

EJ = 8,510⁸(Нсм²)

	2y	+	M	= 0;	y(0) = 0; y(L) = 0 (13.43)
	x2		EJ

Решение.

1. Сравнивая дифференциальное уравнение (13.43) с уравнением (13.28), замечаем, второе уравнение является частным случаем первого, поэтому, вводя в рассмотрение кривизну балки  формулой:

(M[нсм]/E[нсм^-2]J[м⁴]) = [см^-1]=0,00079[см^-1]

можно сразу записать выражение для минимизируемого функционала:

		 =			[	1	(	y	)2	-y]dV
						2		x			(13.44)
			V

2. Обозначим искомую величину прогиба в точке i через Y_i. Точки А, В и С разбивают стержень на 4 конечных одномерных симплекс – элемента , поэтому назначим узлы Y₂ Y₃ Y₄ соответственно в точках А, В и С и узлы Y₁ и Y₅ – в крайних закрепленных точках стержня. Учитывая факт закрепления крайних точек, имеем нулевые перемещения в них под действием момента М, то есть:

Y₁ = 0 и Y₅ = 0

3. Обозначим S – площадь поперечного сечения стержня, L₀ =L/4 – длину конечного элемента. Далее, после замены в формулах (13.32) и (13.33) dV=(Sdx), матрицы элементов примут вид:

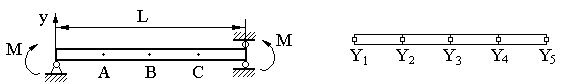Рис. 13.14

[K(е)] = S				{В(e)}T{В(e)}dx		(13.45)
	L(e)
[F(е)] = S					[N(е)]T dх	(13.46)
	L(e)

4. Вычисляем матрицы элементов по указанным формулам.

а) ФФ для каждого элемента в матричной форме примут вид:

[N⁽¹⁾] = [ {1– x/L₀} {x/L₀} ]

[N⁽²⁾] = [ {2 – (x/L₀)} {(x/L₀)–1} ]

[N⁽³⁾] = [ {3 – (x/L₀)} {(x/L₀)–2} ]

[N⁽⁴⁾] = [ {4 – (x/L₀)} {(x/L₀)–3} ]

б) вычисляем матрицы градиентов:

[B⁽¹⁾] = [B⁽²⁾] =[B⁽³⁾] =[B⁽⁴⁾] = [ (–1/L₀) (1/L₀)]

в) учитывая, что элементы матриц градиентов не зависят от координаты x, получим подробно матрицу жесткости для первого конечного элемента:

	L0
[K(1)] = S{В(1)}T{В(1)}		dx = S{В(1)}T{В(1)}L0
	0

Произведение матриц {В⁽¹⁾}^T{В⁽¹⁾} дает следующий результат:

	{В(1)}T{В(1)} =	-1/L0		(-1/L0 ) (1/L0)	=	1/L02	-1/L02
		1/L0				-1/L02	1/L02

Следовательно:

(1)	К(1) =	S	1/L0	- 1/L0
(2)			-1/L0	1/L0

Аналогично получаем матрицы жесткости для остальных конечных элементов

(2)	К(2) =	S	1/L0	- 1/L0
(3)			-1/L0	1/L0
(3)	К(3) =	S	1/L0	- 1/L0
(4)			-1/L0	1/L0
(4)	К(4) =	S	1/L0	- 1/L0
(5)			-1/L0	1/L0

Здесь в правой колонке (в полном соответствии с методом прямой жесткости) указаны номера узлов, необходимые для правильной генерации глобальной матрицы жесткости, причем указанные номера строк совпадают с номерами столбцов матрицы. Результирующая (глобальная) матрица жесткости после сложения полученных локальных матриц примет вид:

			2	-1	0	0	0
K =	S		-1	2	-1	0	0
	L0		0	-1	2	-1	0
			0	0	-1	2	-1
			0	0	0	-1	1

г) вычисляем матрицу нагрузки для первого элемента:

[F(1)] = S



[N(1)]T dх =

L(e)

L0

= S



(1– x/L0)

dx =

SL0

1

(13.46-a)

x/L0

2

1

0

Вычислив аналогично матрицы нагрузки для остальных элементов, получим:

[F(2)] = [F(3)] =		SL0			1
		2			1
[F(4)] =	SL0		1
	2		1