Решение перечисленных задач требует применения методов, с помощью которых можно было бы провести оценку (расчёт) наиболее важных процессов, имеющих место в проектируемом изделии. Это достигается математическим моделированием
| Вид материала | Решение |
| 13.6. Задача изгиба консоли |
- Решение. Из анализа схемы следует, что резисторы, 80.22kb.
- Биохимия нервной ткани, 139.51kb.
- Как провести анализ урока, 130.36kb.
- Решение задач одно из важных применений Excel. Системы линейных уравнений решаются, 39.61kb.
- Контрольные вопросы по дисциплине " экономико- математические методы и модели", 19.66kb.
- Рабочая программа учебной дисциплины компьютерные технологии в науке Кафедра-разработчик, 180.63kb.
- Элективный курс «Компьютерное моделирование физических процессов с помощью математического, 342.03kb.
- Рабочая программа учебной дисциплины компьютерные технологии в науке и производстве, 153.39kb.
- Решение задач по стереометрии, 236.55kb.
- Сопровождение программы: доработка программы для решения конкретных задач, 167.56kb.
Учитывая, что Y1=Y5=0, сокращая на S и подставляя значение L0=L/4, имеем искомую систему алгебраических уравнений:
-
2
-1
0
Y2
= (L2/8)
1
-1
2
-1
Y3
1
0
-1
2
Y4
1
д) подставляя численные значения ((L2/8)=2,25см) и решая систему уравнений, получаем следующие перемещения точек: Y2 = Y4 = 3,375 см, Y3=4,5 см.
13.6. Задача изгиба консоли
Условие задачи. Консоль длиной L=150 см жестко закреплена в точке х=0 и подвержена действию сосредоточенной величиной F=4500 Н на свободном конце. Точки А, В, C, D делят балку на 5 равны[ частй. Прогиб балки Y(x) описывается дифференциальным уравнением вида (13.47). Требуется определить прогибы консоли в точках А, В … Е, если изгибная жесткость стержня равна: EJ = 8,5108(Нсм2)
| | 2y | - | M | = 0; | y(0) = 0; | (13.47) | |
| x2 | EJ | ||||||
| | Решение. | ||||||
1. Дифференциальные уравнения (13.47) и (13.43) отличаются лишь знаком момента, поэтому для решения данной задачи можно использовать ту же вариационную трактовку задачи, если ввести следующее обозначение для кривизны балки : M(х)/EJ = -(х). Очевидно, что в отличие от предыдущей задачи здесь момент М(х), создаваемый силой F, меняется прямо пропорционально длине стержня. Эпюра моментов, построенная по формуле: M(х)=F(L-x), приведена справа на рисунке 13.15. Числовые значения моментов в узловых точках приведены в таблице:
-
Узел
=М/EJ [см-2]
Узел
=М/EJ [см-2]
1
-0,000794
4
-0,000318
2
-0,000635
5
-0,000159
3
-0,000476
6
-0,000000
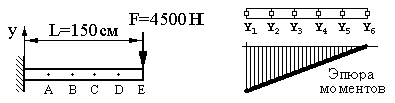 |
| Рис. 13.15 |
2. Обозначая искомую величину прогиба в точке i через Yi, оставляем предыдущее разбиение стержня в точках А, В … Е на 5 элементы длиной L0=18,75см каждый. Учитывая закрепление левой точки, имеем: Y1 = 0.
3. Составляем уравнения, соответствующие первому элементу, для чего:
- записываем его матрицу жесткости, найденную в предыдущей задаче:
| (1) | К(1) = | S | 1/L0 | - 1/L0 | | |
| (2) | -1/L0 | 1/L0 | | |
- для формирования вектора нагрузки 1-го элемента, учитывая зависимость момента от координаты х, надо формулу (13.46) преобразовать к виду:
| | L0 | | | ||
| [F(1)] = S | | (х)[N(1)]T dх | | ||
| | 0 | | |||
Кривизна балки внесена под знак интеграла, так как она линейно зависит от х. Выразим ее через узловые значения с помощью линейного интерполяционного многочлена: (х) = N11 + N22
Вспоминая формулу (12.25), вычислим интеграл в формуле вектора нагрузки:
| [F(1)]=SL/6 | 2 | 1 | | 1 | | |
| 1 | 2 | 2 |
Наконец, подключая вектор неизвестных, и проводя сокращение на S, получаем следующую систему уравнений 1-го элемента в общем виде:
| | 1 | -1 | | Y1 | = | L2 | | (21+2) |
| -1 | 1 | Y2 | 6 | | (1+22) |
Подставляя числовые значения 1 и 2 из таблицы и длину элемента L=30 см, получим окончательную систему уравнений для 1-го элемента:
| | 1 | -1 | | Y1 | = | 0,33345 |
| -1 | 1 | Y2 | 0,30960 |
Аналогично получаем уравнения для остальных конечных элементов:
| | 1 | -1 | | Y2 | = | 0,26190 |
| -1 | 1 | Y3 | 0,23805 |
| | 1 | -1 | | Y3 | = | 0,19050 |
| -1 | 1 | Y4 | 0,16680 |
| | 1 | -1 | | Y4 | = | 0,11925 |
| -1 | 1 | Y5 | 0,09540 |
| | 1 | -1 | | Y5 | = | 0,04770 |
| -1 | 1 | Y6 | 0,02385 |
Применяя метод прямой жесткости, приходим к системе:
-
1
-1
0
0
0
0
Y1
=
0,33345
-1
2
-1
0
0
0
Y2
0,57150
0
-1
2
-1
0
0
Y3
0,42855
(13.48)
0
0
-1
2
-1
0
Y4
0,28605
0
0
0
-1
2
-1
Y5
0,14310
0
0
0
0
-1
2
Y6
0,02385
Левый конец стержня закреплен, поэтому Y1=0. Из первого уравнения имеем Y2 = - 0,33345 [см], (-0,3335). Здесь и далее в скобках приведены теоретические значения прогибов. Последовательно находим: из второго уравнения: Y3 = 2Y2 – 0,57150 =–0,66690 – 0,57150 = –1,2384 [см]; (1,2388); из третьего: Y4 = –Y2 + 2Y3 – 0,42855 =
= –(– 0,33345) + 2(–1,2384) – 0,42855= -2,5719 [см] ; (2,5729)
Аналогично далее: Y5 =-4,1929 [см] ; (4,1929) и Y6 =-5,9550 [см] ; (5,9559)
14. Размещение матрицы жесткости в ОЗУ ЭВМ
Выше уже отмечалось, что ленточный характер матрицы жесткости позволяет значительно сократить объем памяти для ее хранения. Эффективная программа не хранит целиком глобальную матрицу жесткости и не хранит даже ее половину. Более того эффективная программа вообще не рассматривает как отдельные массивы с заранее заданными размерами матрицу жесткости, глобальный вектор нагрузки и вектор решения. Программа хранит все эти величины в общем одномерном массиве, размер которого определяется программой при ее выполнении (операторы new и dispose). Проиллюстрируем сказанное на примере размещения в ОЗУ рассмотренной выше системы уравнений (14.2). С этой целью запишем систему (14.2) в матричном виде, округлив для краткости изложения коэффициенты матрицы жесткости до целых:
-
47
-22
0
0
T1
=
1000
(14.3)
-22
93
-22
0
T2
2000
0
-22
+93
-22
T3
2000
0
0
-22
57
T4
1400
Полоса в матрице жесткости выделена жирным курсивом и, очевидно, имеет ширину, равную двум. Поэтому для ее хранения достаточно двух строк:
-
[
47
93
93
57
]
(14.4)
-22
-22
-22
x
