Решение перечисленных задач требует применения методов, с помощью которых можно было бы провести оценку (расчёт) наиболее важных процессов, имеющих место в проектируемом изделии. Это достигается математическим моделированием
| Вид материала | Решение |
- Решение. Из анализа схемы следует, что резисторы, 80.22kb.
- Биохимия нервной ткани, 139.51kb.
- Как провести анализ урока, 130.36kb.
- Решение задач одно из важных применений Excel. Системы линейных уравнений решаются, 39.61kb.
- Контрольные вопросы по дисциплине " экономико- математические методы и модели", 19.66kb.
- Рабочая программа учебной дисциплины компьютерные технологии в науке Кафедра-разработчик, 180.63kb.
- Элективный курс «Компьютерное моделирование физических процессов с помощью математического, 342.03kb.
- Рабочая программа учебной дисциплины компьютерные технологии в науке и производстве, 153.39kb.
- Решение задач по стереометрии, 236.55kb.
- Сопровождение программы: доработка программы для решения конкретных задач, 167.56kb.
Вычисляем матрицу жесткости для каждого конечного элемента, используя выражение (13.32).
Для первого элемента матрица градиентов примет вид:
| | {В(1)} = | { | N1(1) | | N2(1) | 0 | N4(1) | 0 | 0 | } | (13.34) |
| | x | | x | x | |||||||
| | N1(1) | | N2(1) | 0 | N4(1) | 0 | 0 | ||||
| | y | | y | y |
Для треугольного симплекс - элемента, имеющего упорядоченную нумерацию узлов (i, j, k), ранее получено выражение (9.11) для коэффициента формы. В частности для точки k имеем:
Nk = 0,5 А –1 [ak + bk x + ck y], (13.35)
где коэффициенты ak , bk и ck рассчитываются с учетом обхода узлов внутри симплекс – элемента строго против часов, начиная с точки k по формулам:
ak = Xi Yj – Xj Yi; bk = Yi – Yj; ck = (Xj – Xi)
Учитывая, что площадь любого конечного элемента равна:
А = (¼ ) ( ¼ ) ( ½) = 32 –1 (13.36)
и при дифференцировании по х выражения (13.35) в результате останется лишь коэффициент bk, получим верхнюю строку матрицы градиентов (13.34) в виде:
| | | [N(1)] | = 16 [b1 b2 0 b4 0 0] = [- 4 4 0 0 0 0] | | |
| | | x |
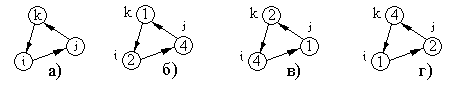 |
| Рис. 13.8 |
Значения для коэффициентов b получим по формулам:
b1 = Y2 – Y4 = - ¼; b2 = Y4 – Y1= + ¼ и b4 = Y1 – Y2= 0.
Нумерация индексов здесь принята в строгом соответствии с порядком обхода узлов, показанная на рисунке 13.8. Например, при вычислении коэффициента b2 в качестве k – го узла в формуле bk = Yi – Yj; принят узел 2, за которым на рисунке 13.8-в следует узел i=4 и j=1.
Аналогично вычисляем нижнюю строку матрицы (13.34), в которой при дифференцировании по y выражения (13.35) останется только коэффициент ck:
| | | [N(1)] | = 16 [c1 c2 0 c4 0 0] = [0 - 4 0 4 0 0] | | |
| | | y |
Как и в предыдущем случае, значения для коэффициентов с получим по формулам: с1 = X4 – X2 = 0; с2 = X1 – X4= - ¼; и с4 = X2 – X1= - ¼ с соблюдением того же порядка обхода узлов.
Таким образом, матрица градиентов для первого элемента примет вид:
| | | {В(1)} | = | -4 4 0 0 0 0 | (13.37) |
| | | 0 -4 0 4 0 0 |
В выражение (13.32) для матрицы жесткости элемента (МЖЭ) входит произведение: {В(1)}Т{В(1)}. Для его вычисления вспомним правило перемножения двух матриц на примере:
-
a b
ax+bu
ay+bv
az+bw
x y z
c d
=
cx+du
cy+dv
cz+dw
u v w
e f
ex+fu
ey+fv
ez+fw
Искомое произведение матриц примет вид:
-
-4
0
16
-16
0
0
0
0
4
-4
-16
32
0
-16
0
0
0
0
-4
4
0
0
0
0
=
0
0
0
0
0
0
0
4
0
-4
0
4
0
0
0
-16
0
16
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
Принимаем толщину элемента, равной единице, и выносим произведение матриц за знак интеграла (13.32). В результате dV становиться равным 1/32. Следовательно, МЖЭ для первого конечного элемента:
-
К(1) = ½
1
-1
0
0
0
0
-1
2
0
-1
0
0
0
0
0
0
0
0
0
-1
0
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
Для вычисления объемного интеграла (13.33) в матрице нагрузки воспользуемся интегральной формулой вычисления площади треугольника с применением системы L –координат. Последняя представляет собой совокупность трех относительных координат точки R внутри треугольника L1, L2 и L3, каждая из которых является отношением расстояния от точки А до одной из сторон треугольника. Если A – площадь треугольника, то L – координата точки R относительно стороны (i, j) равна L1=А1/A. Можно показать, что переменные L1, L2 и L3 представляют собой ФФ для треугольного симплекс – элемента. Это обстоятельство вкладывает дополнительный смысл в понятие ФФ треугольного элемента. Например, для рисунка 13.9 имеем: L1= Nk.
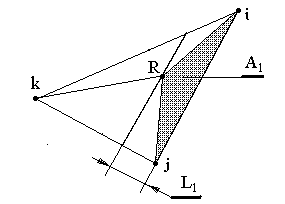 |
| Рис. 13.9 |
Преимущество L – координат проявляется при необходимости вычисления интегралов вдоль сторон конечного элемента и по его площади. Так, если A, B, и С – целые числа, то справедлива следующая интегральная формула:
| | | | L1A L2B L3C dA = | A! B! C! | 2A | | | (13.38) | ||||
| | | (A+B+C+2)! | | | ||||||||
| | | А | | | | | | | | | | |
Чтобы воспользоваться формулой (13.38) необходимо подынтегральное выражение выразить через L – координаты. Вычислим в качестве примера следующий интеграл по площади А:
- Ni Nj dA = (L11 L21 L30) dA = { 1!1!0!/(1+1+0+2)! }2A = 2A/4!=A/12.
В текущем примере надо вычислить интеграл (13.33). Вычислим вначале:
- Ni dA = (L11 L20 L30) dA = { 1!0!0!/(1+0+0+2)! }2A = 2A/3!=A/3.
Запишем интеграл (13.33) в развернутом виде для первого элемента:
| | | | | | | | | N1(1) | | | | |
| | | | | | | | N2(1) | | | | | |
| | | | f(1) = | 2G(1) | 0 | dV | | (13.39) | ||||
| | | | | | | N4(1) | | | ||||
| | | | | V | | | 0 | | | | | |
| | | | | | | | 0 | | | | | |
Заменяя ФФ L – координатами: L1=N1 (1),L2=N2 (1), L3=N4 (1), имеем:
| | | | f(1) = | 2G(1)A | [ 1 1 0 1 0 0 ]T | | | | | |
| | | | 3 | | | | |
