Решение перечисленных задач требует применения методов, с помощью которых можно было бы провести оценку (расчёт) наиболее важных процессов, имеющих место в проектируемом изделии. Это достигается математическим моделированием

Вид материала

Решение

Содержание Основы теории принятия решений Постановка задачи оптимизации при решении ЗПР. Метод прямого дифференцирования. Метод Лагранжа

Подобный материал:

• Решение. Из анализа схемы следует, что резисторы, 80.22kb.
• Биохимия нервной ткани, 139.51kb.
• Как провести анализ урока, 130.36kb.
• Решение задач одно из важных применений Excel. Системы линейных уравнений решаются, 39.61kb.
• Контрольные вопросы по дисциплине " экономико- математические методы и модели", 19.66kb.
• Рабочая программа учебной дисциплины компьютерные технологии в науке Кафедра-разработчик, 180.63kb.
• Элективный курс «Компьютерное моделирование физических процессов с помощью математического, 342.03kb.
• Рабочая программа учебной дисциплины компьютерные технологии в науке и производстве, 153.39kb.
• Решение задач по стереометрии, 236.55kb.
• Сопровождение программы: доработка программы для решения конкретных задач, 167.56kb.

Основы теории принятия решений

Принять правильное решение — значит выбрать такую альтернативу из числа возможных, в которой, с учетом различных влияющих факторов, будет оптимизирована некоторая ценность. Если оптимальное решение найдено в заданное время и при заданных затратах, то такое решение называют инженерным. В общем случае задача принятия решения (ЗПР) возникает в том и только в том случае, если существуют:

• цель, которую нужно достичь, учитывая влияющие факторы
  
• различные способы достижения цели.
  

Влияющие факторы могут влиять на целевую функцию в различных направлениях.

Пример:

Повысить надежность системы можно за счет увеличения числа резервных блоков, но при этом растет общий вес, поэтому принимаемое решение обычно является компромиссным.

До тех пор, пока стоимость компромисса меньше либо равна количеству имеющихся средств, с ним соглашаются. В противном случае на смену качественному приходит количественный анализ с применением научных методов теории оптимизации.

Постановка задачи оптимизации при решении ЗПР.

Необходимо определить значения параметров (x1, x2, …, xn) целевой функции V(x) = V(x1, x2, …, xn), при которых V(x) достигает экстремального значения и одновременно удовлетворяет следующему ряду ограничений:

f1(x1, x2, …, xn) = 0, f1 < 1

f2(x1, x2, …, xn) = 0, f2 > 2

m) fm(x1, x2, …, xn) = 0, fm < m

Среди методов решения задач оптимизации рассмотрим следующие методы:

• метод прямого дифференцирования, метод множителей Лагранжа
  
• симплекс – метод , метод градиента
  

Метод прямого дифференцирования. Применим в тех случаях, когда отсутствуют функциональные ограничения и целевая функция дифференцируется.Пример:Известно, что стоимость изделия в эксплуатации обратно пропорциональна его надежности, т.е.(Т1).

Чем выше вероятность безотказной работы, тем выше стоимость изделия в производстве, (Т2).

Суммарная стоимость зависит от P: (Т3). И суммарная (Т4)

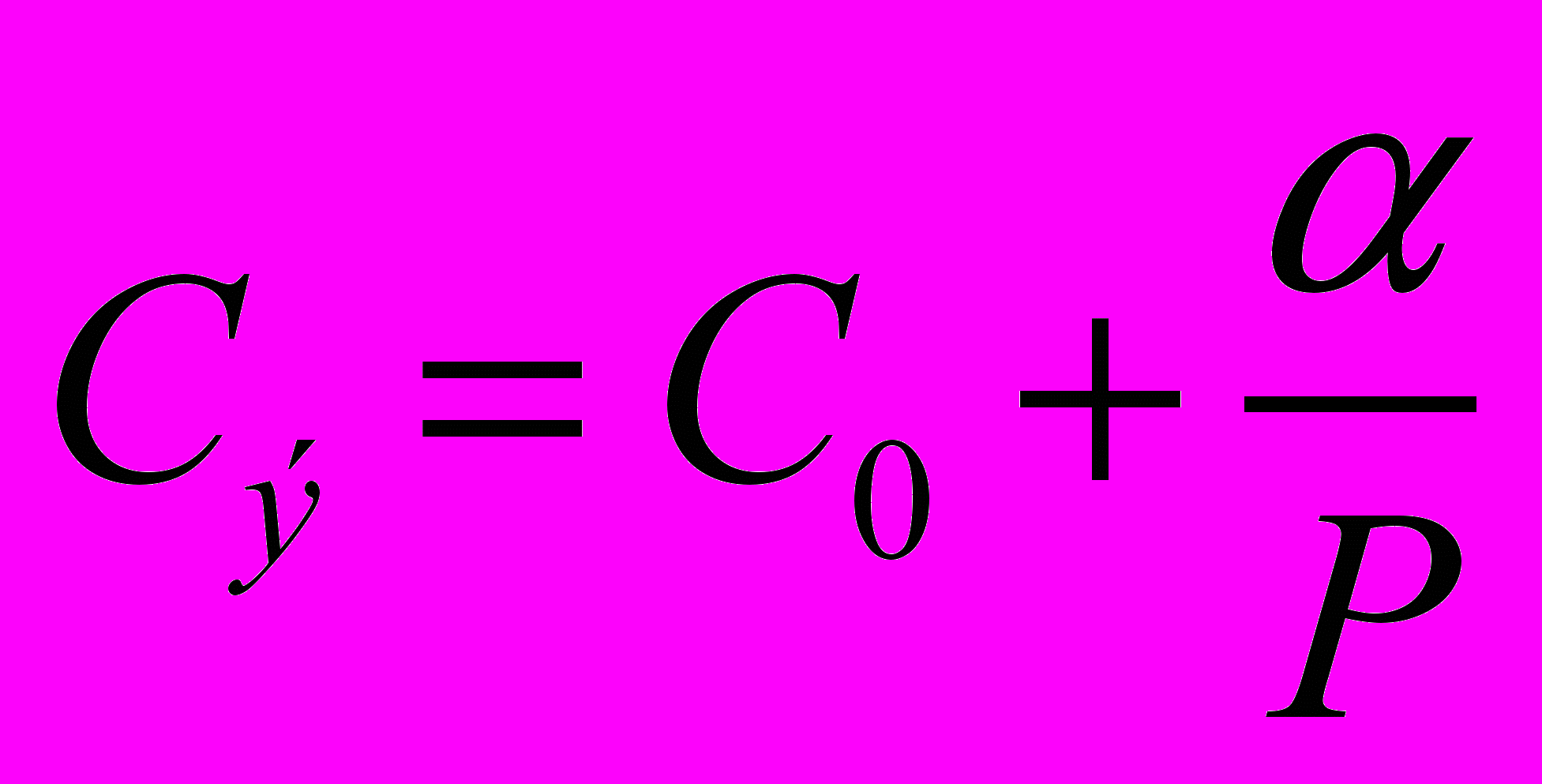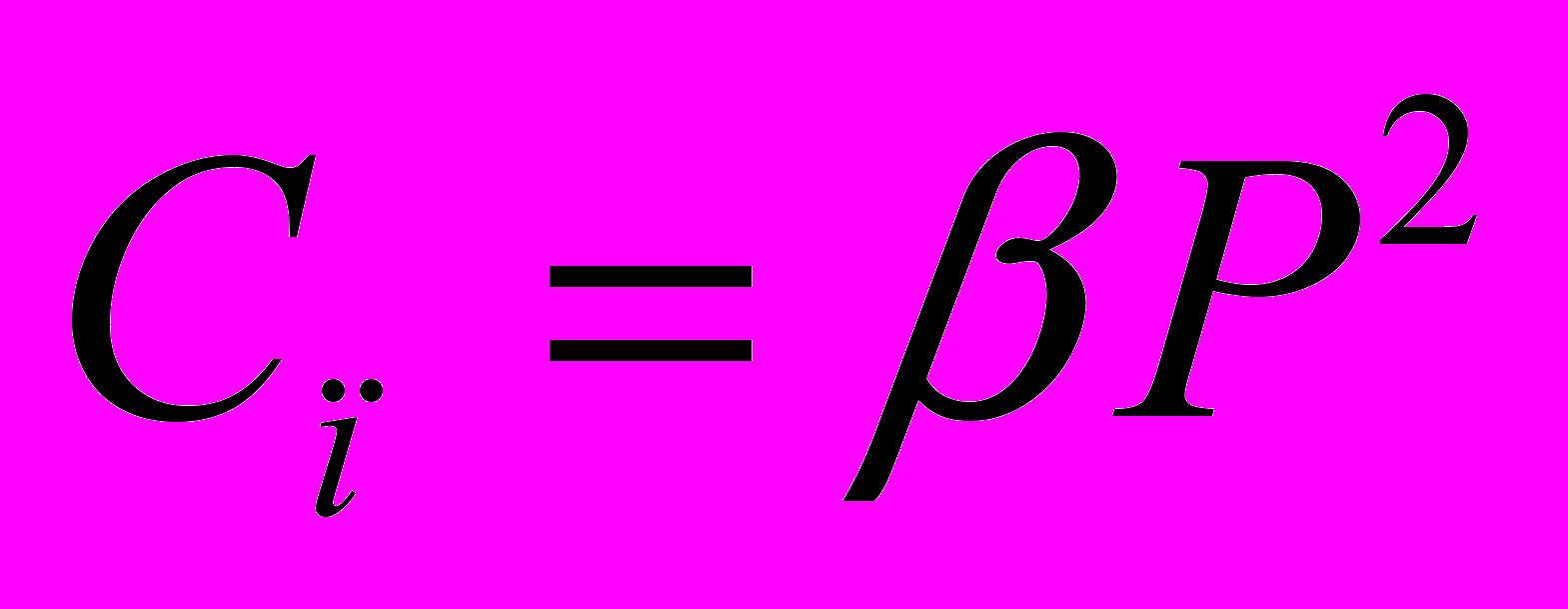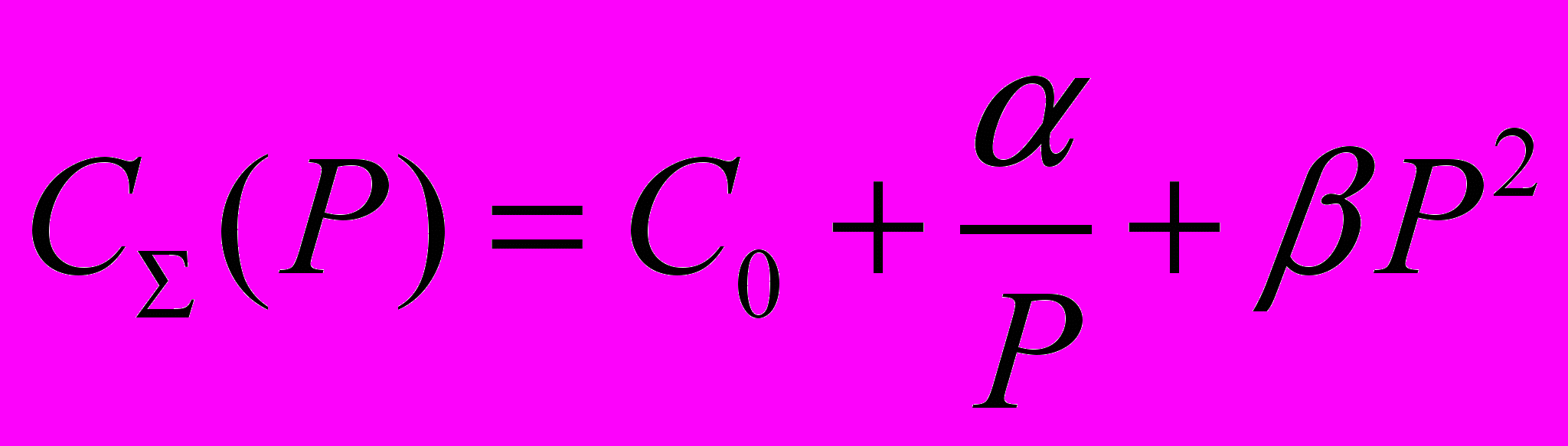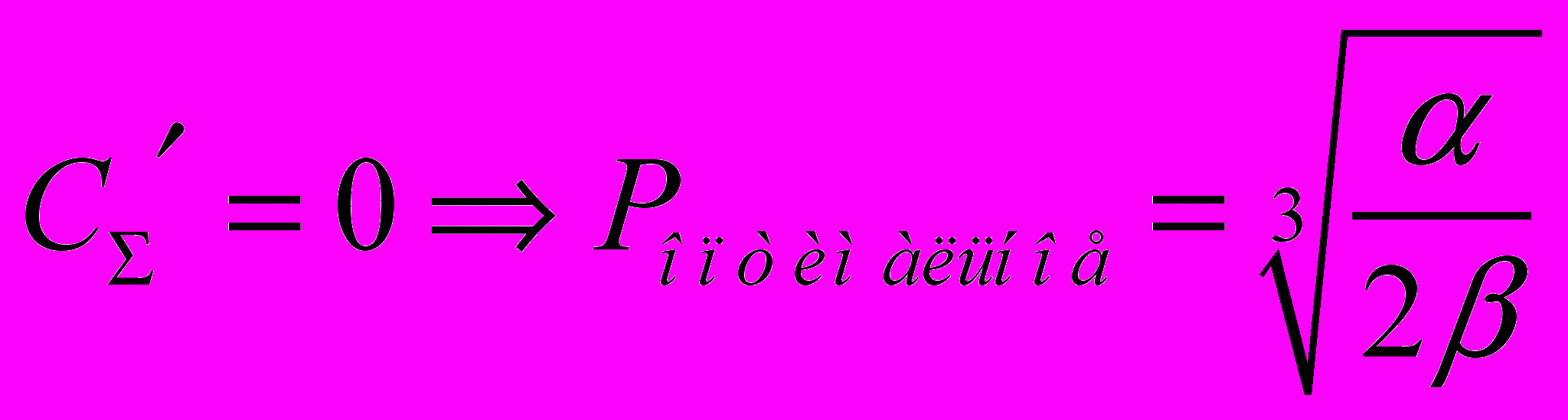Метод Лагранжа

Метод применим, если на целевую функцию наложены ограничения в виде равенств.Метод Лагранжа:

Составляется функция Лагранжа:

,

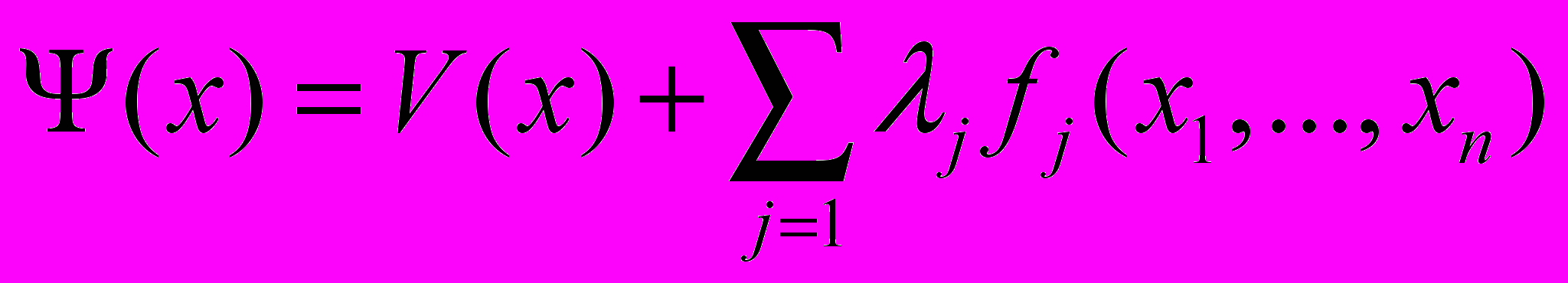где j — неопределенные множители Лагранжа.

Составляется система (n+m) уравнений вида:



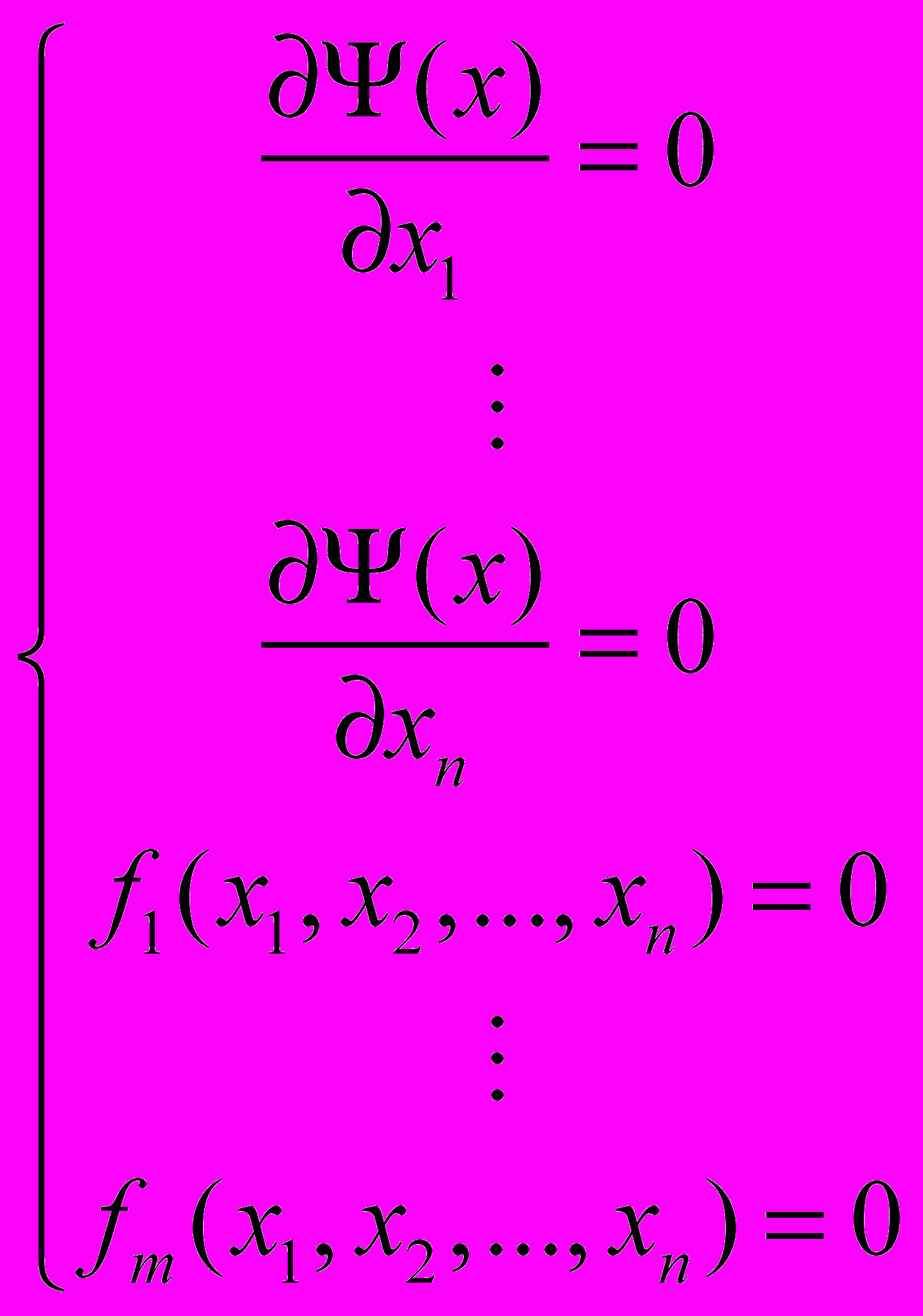
Пример:

Определить минимальные веса резерва при заданном уровне надежности.

Пусть ЭВМ состоит из двух блоков. Если отказ одного из блоков ведет к отказу всей ЭВМ, то вероятность безотказной работы ЭВМ будет равна P=P1P2, где P1, P2 — вероятности безотказной работы первого и второго блоков соответственно. Если q1, q2 — вероятности отказа первого или второго блока соответственно, то вероятность безотказной работы всей ЭВМ: P=(1-q1)(1-q2)=1-(q1+q2)+q1q2=1-(q1+q2).

Пусть рассматриваемая ЭВМ будет высоконадежной, то есть Pi>0,9.

Если ЭВМ состоит из n блоков, то при высоком уровне надежности можно принять P=1-qi.

Пусть ri — кратность резервирования i-го блока, т.е. количество дополнительных блоков, включенных параллельно c i-м.

Тогда вероятность отказа всего резервированного блока равна: 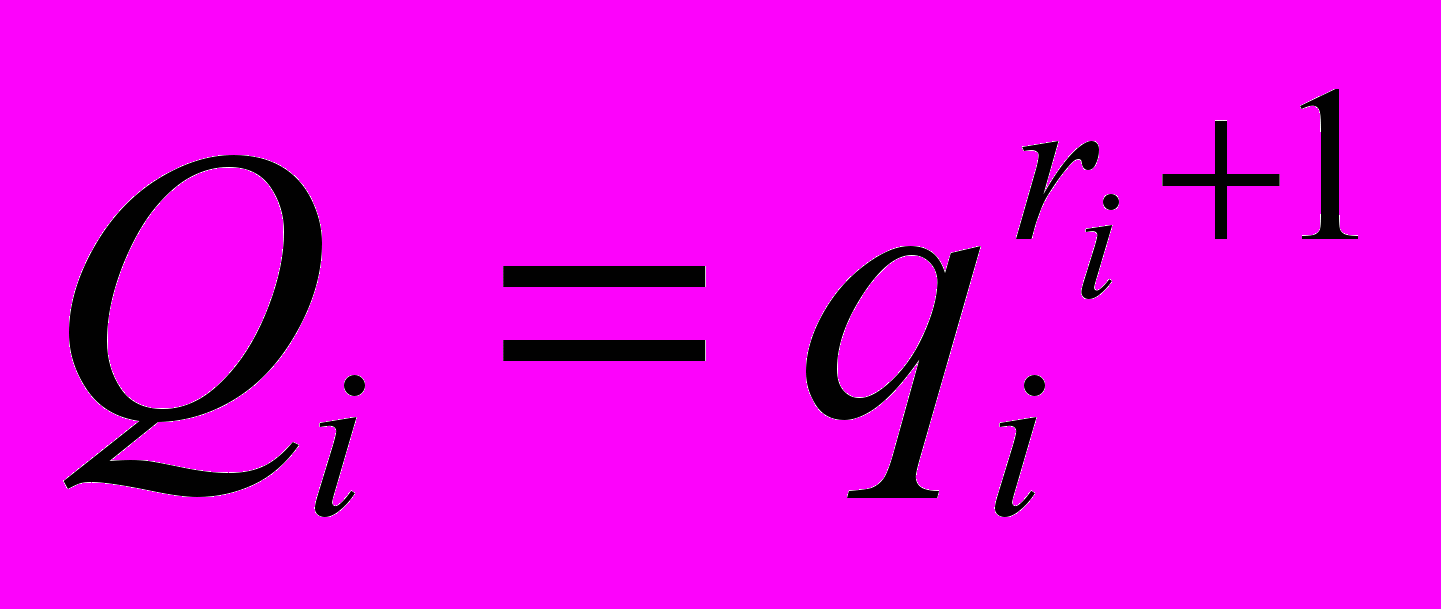. Таким образом, .

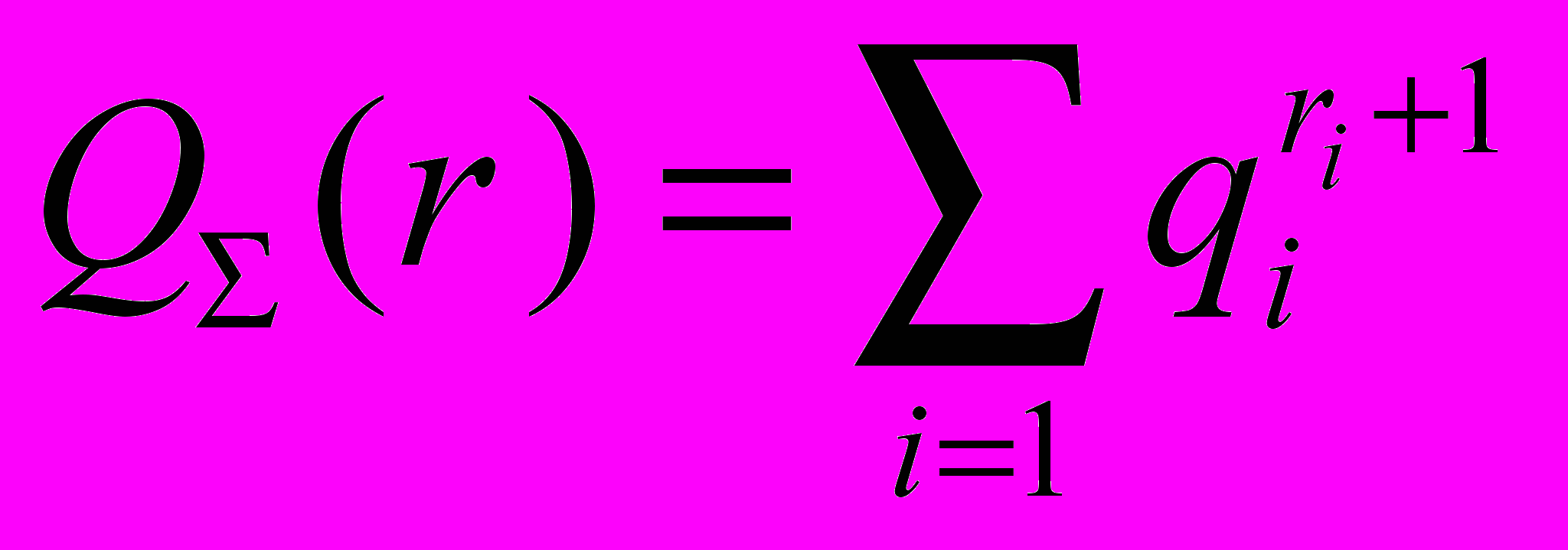Вес резерва 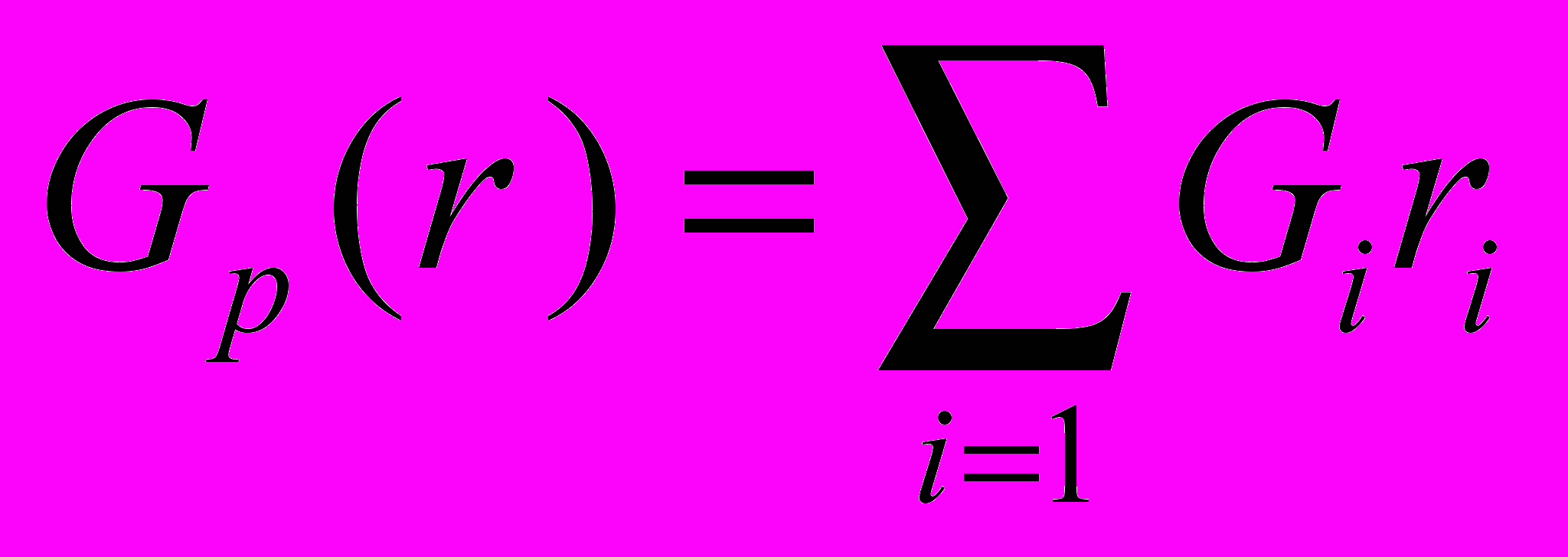, где Gi — вес нерезервированного блока.

Так как по условию задачи задан уровень надежности, то Q является ограничением, а Gp — целевой функцией.

Составим функцию Лагранжа: .

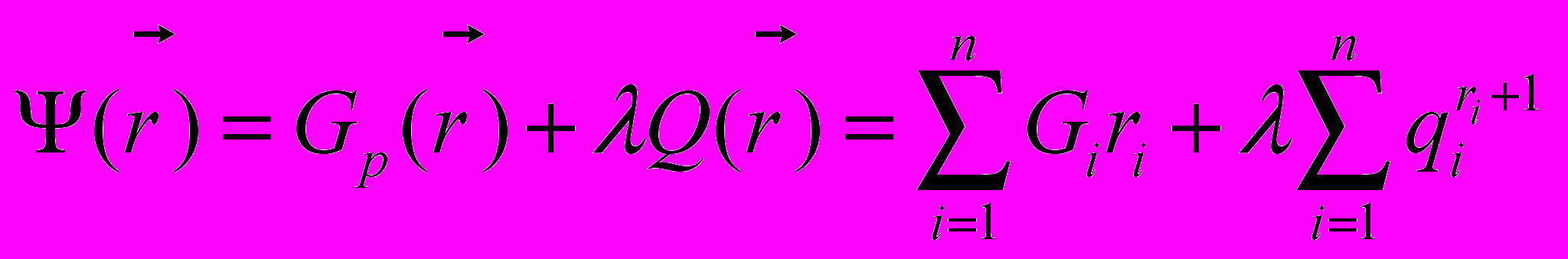Составляем систему из n уравнений, дифференцируя функцию Лагранжа по каждой неизвестной ri: 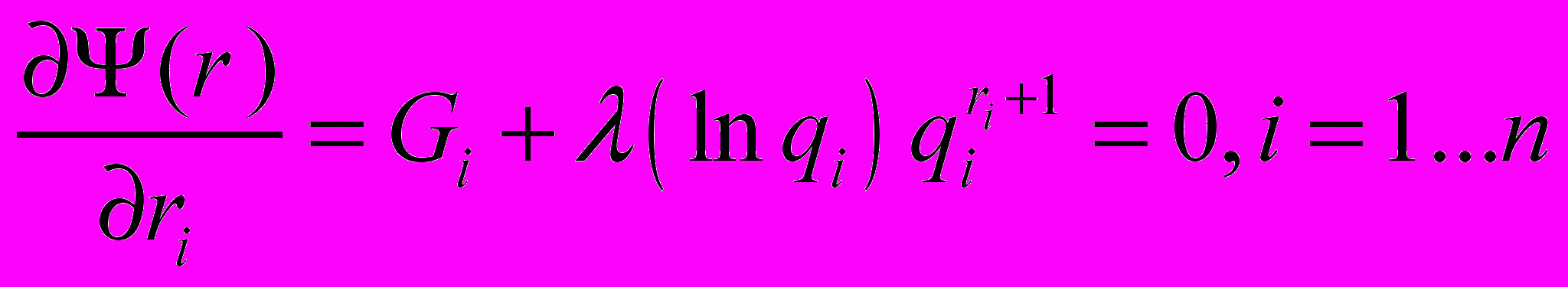, откуда 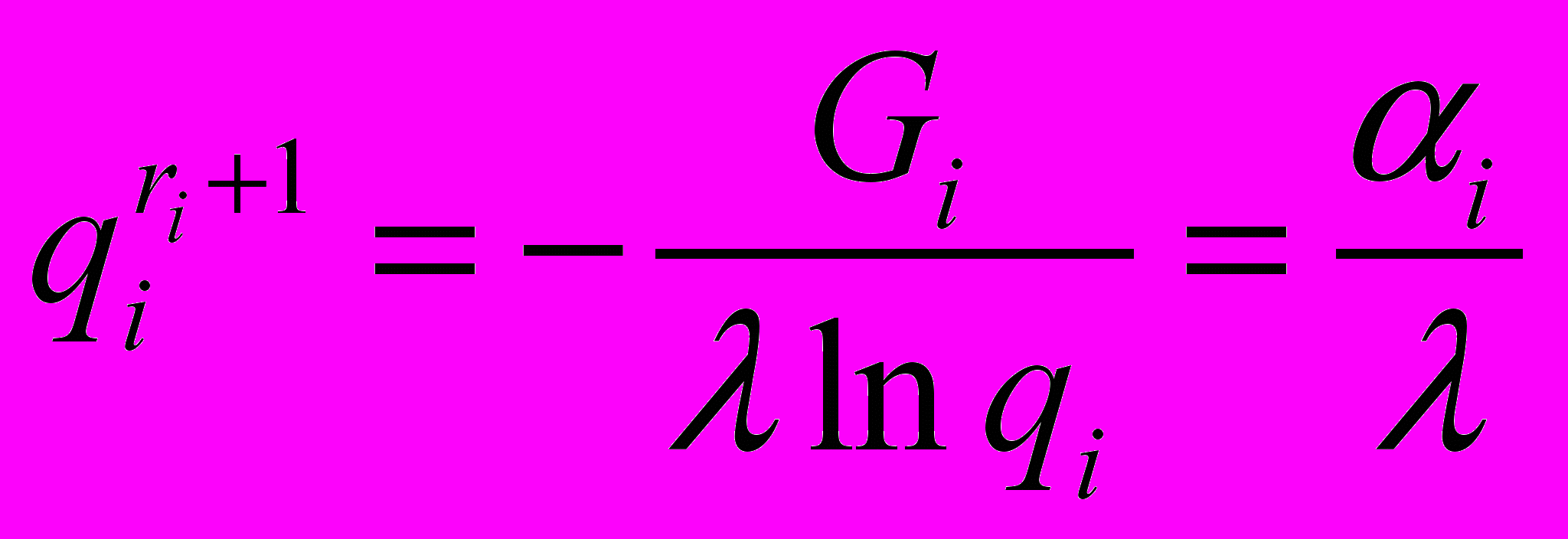, где .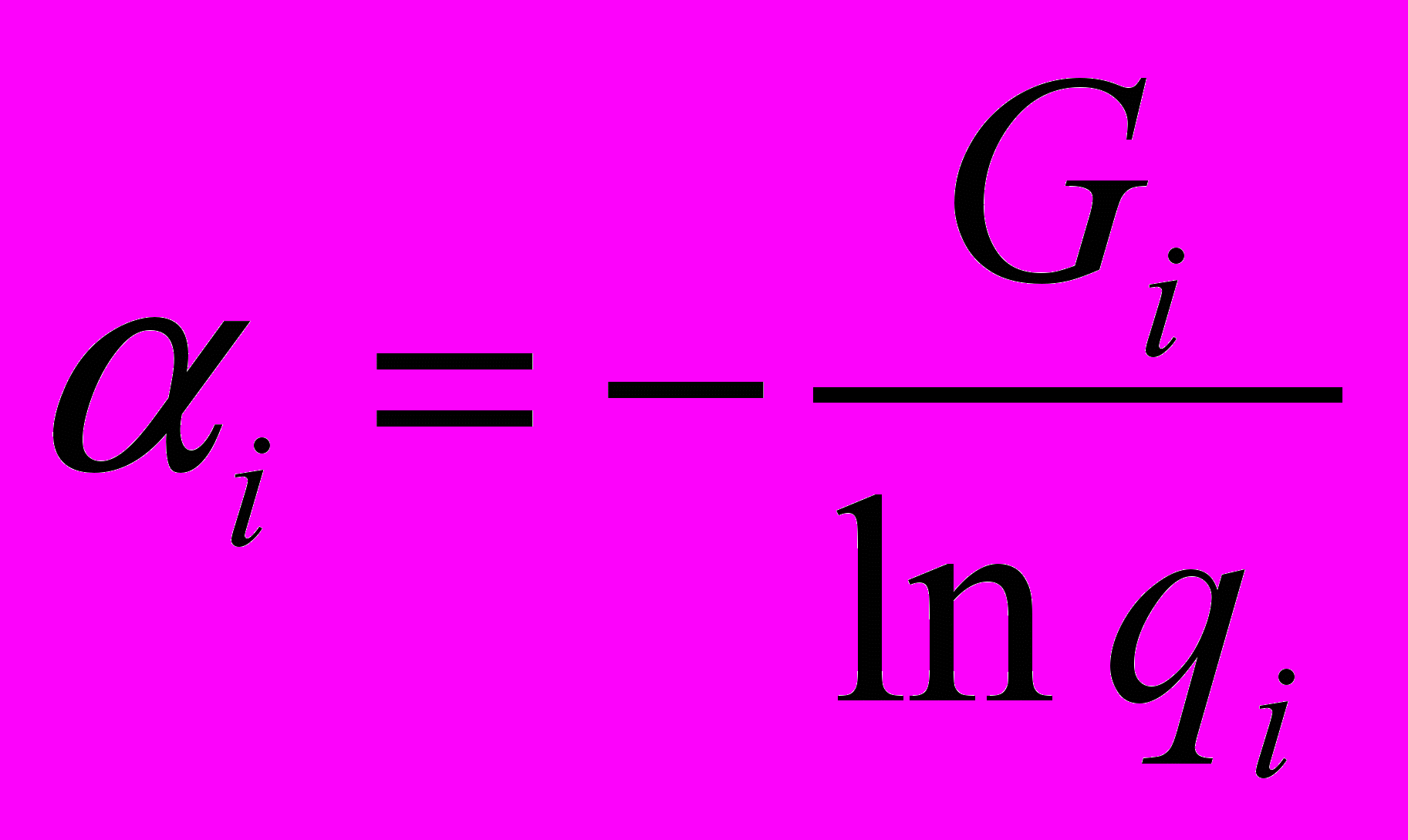

Неопределенный множитель Лагранжа вычислим, подставляя 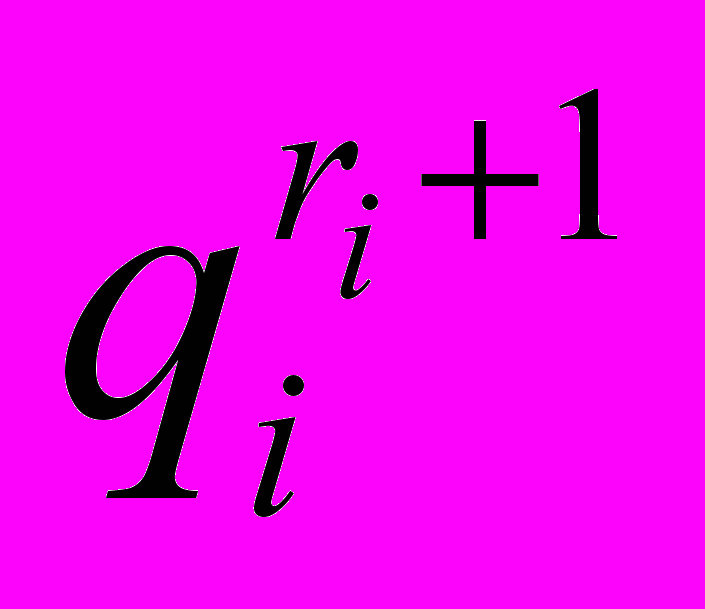в функциональное ограничение: 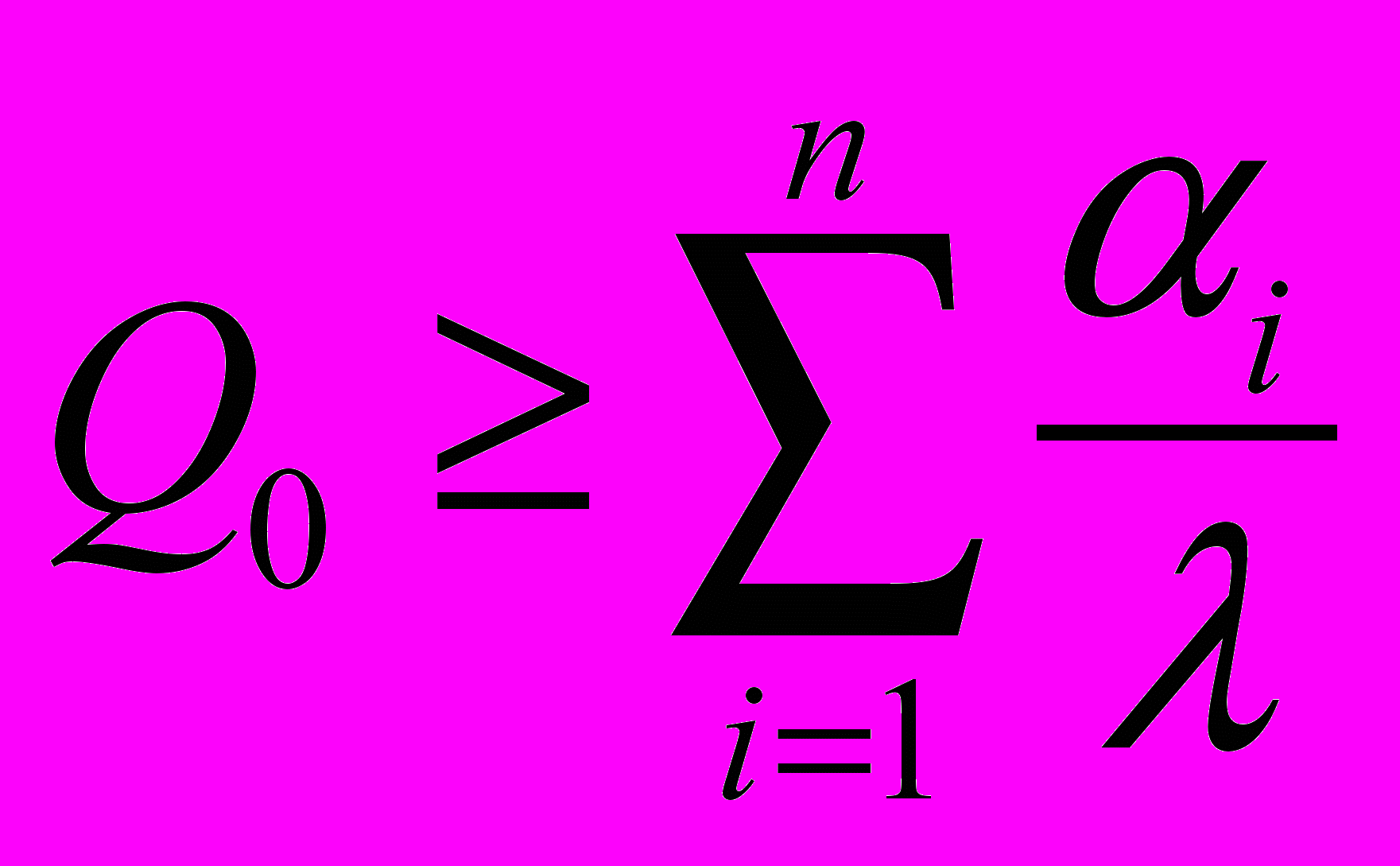. Пусть .

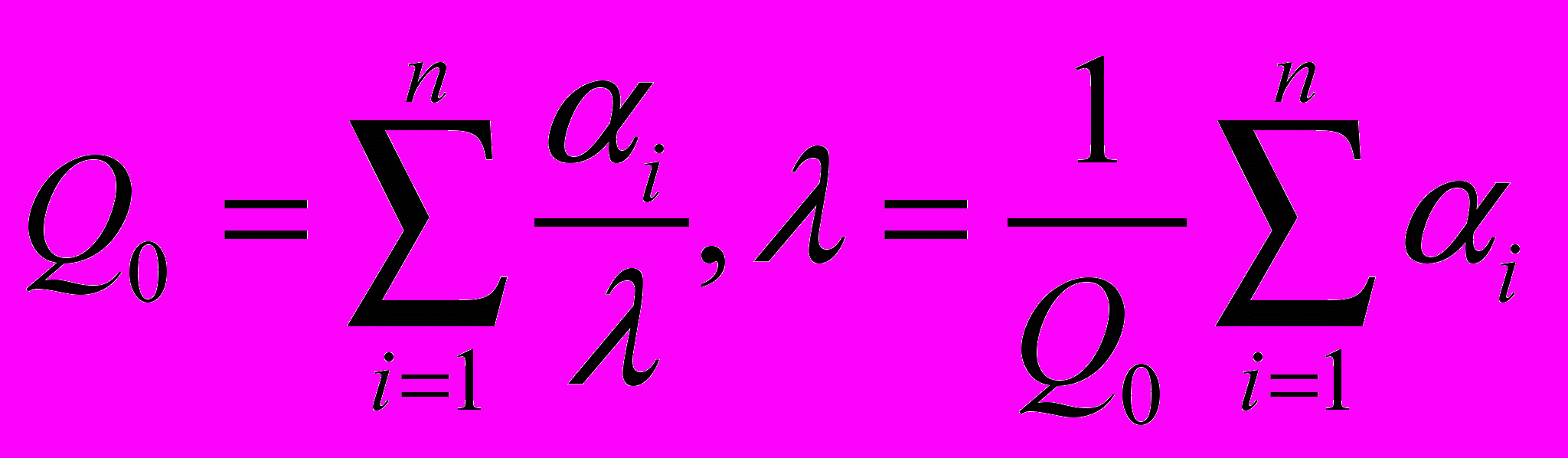Определим теперь коэффициент ri: 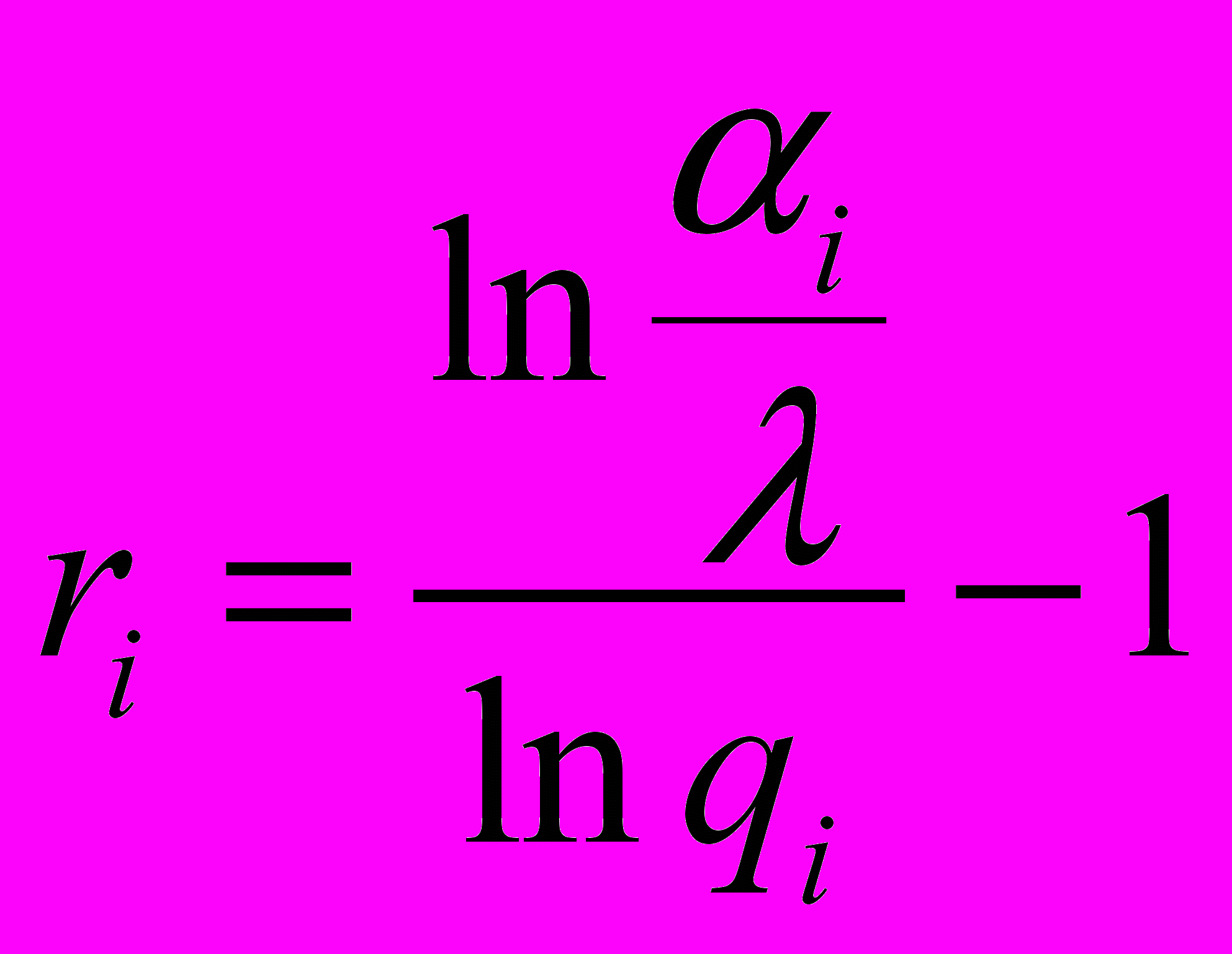. Полученные значения ri могут оказаться дробными.

Рассмотрим числовой пример.

Система состоит из 3-х блоков, P  0,9.

G1=1	G2=3	G3=1
q1=0,3	q2=0,5	q3=0,5

При каких ri будет обеспечен заданный уровень надежности и минимальный вес? Решение.

Вычисляем i: .

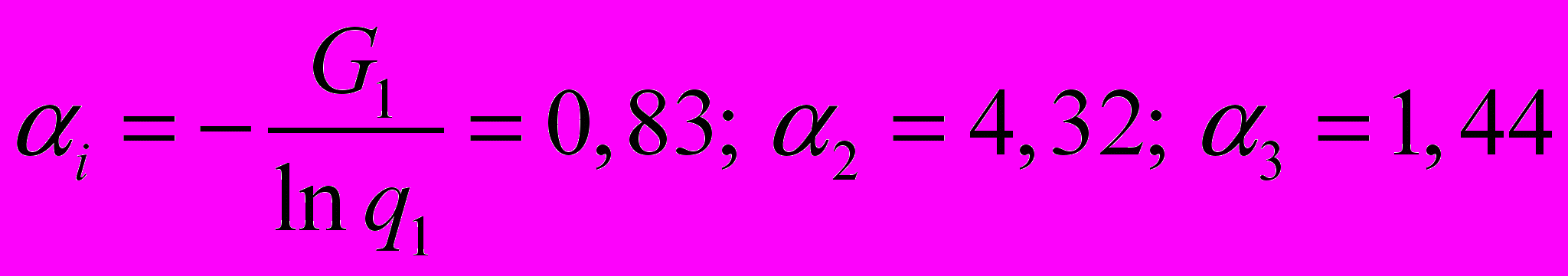Определяем :



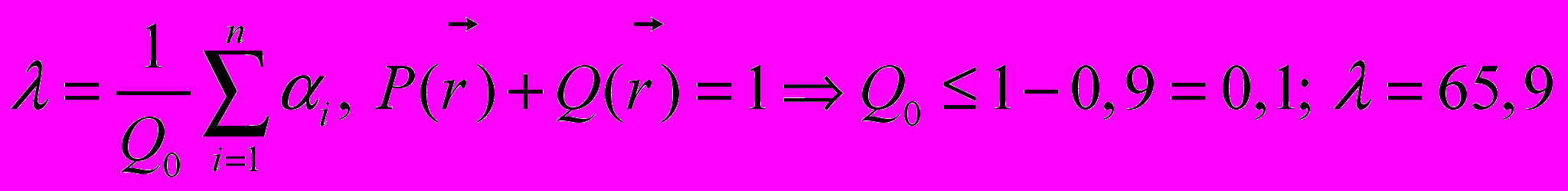
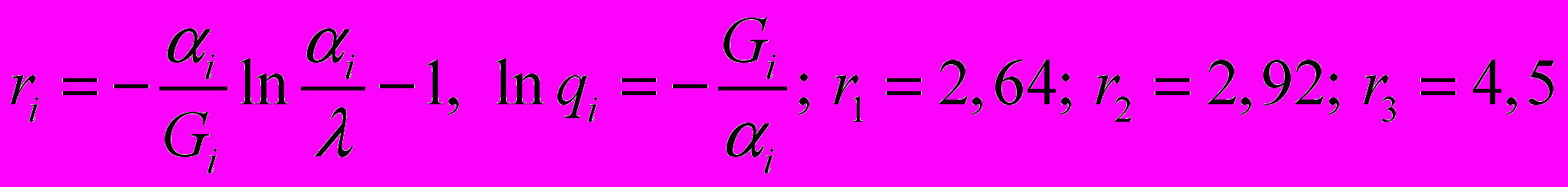
Составляем таблицу для перебора оставшихся вариантов и выбора оптимального:

№	r1	r2	r3
1	2	2	4
2	2	2	5
3	2	3	4
4	2	3	5
5	3	2	4
6	3	2	5
7	3	3	4
8	3	3	5

Варианты 1,2,3,4,5 не удовлетворяют требованиям надежности. ИЗ оставшихся выбираем вариант с наименьшим весом.