Учебно-методический комплекс для студентов специальностей: 080801 «Прикладная информатика в экономике», 080103 «Национальная экономика», 080107 «Налоги и налогообложение», 080111 «Маркетинг», 080507 «Менеджмент организации»
| Вид материала | Учебно-методический комплекс |
- Учебно-методический комплекс для студентов специальностей: 080801 «Прикладная информатика, 783.55kb.
- Учебно-методический комплекс для студентов специальностей 080507 Менеджмент организации,, 1709.91kb.
- С. И. Качин 2010г, 271.16kb.
- Учебно-методический комплекс для студентов специальностей 080507 «Менеджмент организации»,, 1534.42kb.
- Учебно-методический комплекс для студентов специальности 080103 «Национальная экономика»,, 497.11kb.
- Учебно-методический комплекс Специальность: 080801 Прикладная информатика (в экономике), 325.69kb.
- Учебно-методический комплекс Для специальности: 080801 «Прикладная информатика (в экономике)», 357.03kb.
- Учебно-методический комплекс Для специальностей: 030501 Юриспруденция 080801 Прикладная, 498.9kb.
- Учебно-методический комплекс для студентов специальностей 080103 «Национальная экономика»,, 403.77kb.
- Учебно-методический комплекс Для студентов специальности 080801 Прикладная информатика, 489.42kb.
Тесты
- Определить, где мы имеем дело с последовательностью независимых испытаний :
- Из урны, где лежит 5 красных и 4 черных шара последовательно , один за другим вытаскивают шары и отмечают.
- Из той же урны вынимают шары, но каждый шар после вынимания отмечается и затем кладется обратно, после чего наугад вынимается следующий.
- Одну монету подбросили 10 раз.
- Подбросили разом 10 монет.
- Из урны, где лежит 5 красных и 4 черных шара последовательно , один за другим вытаскивают шары и отмечают.
- Два стрелка выстрелили один раз по мишени . При этом возможны следующие события:
А=ни один не попал; В=первый попал; С=второй попал; Д=попал только первый; Е=попал только второй; Ж=попал один из стрелков; З=попали оба стрелка . Выделите правильные соотношения между событиями : 1) Д=ВС; 2) Ж=С+ВС; 3) З=ВС
- Д=ВС; 5) Ж=ВД+ВС; 6) З=ДЕ;
7) Д=В+С; 8) Ж=ВДС; 9) З=А-Ж; 10)Ж=З-А .
3. Выделить те утверждения ,которые относятся к аксиомам теории вероятностей:
1) P(
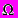 )=1; 2) P(A+B)=P(A)+ P(B) для несовм. cобытий; 3) P(A+B)=P(A)+P(B)-P(AB); 4) P(AB)=P(A)P(BA); 5) P(B-A)=P(B)-P(A).
)=1; 2) P(A+B)=P(A)+ P(B) для несовм. cобытий; 3) P(A+B)=P(A)+P(B)-P(AB); 4) P(AB)=P(A)P(BA); 5) P(B-A)=P(B)-P(A).4. События называются несовместными если:
1) Они не могут произойти.
2) Одно из них является невозможным.
3) Они не могут произойти одновременно.
- нет верных ответов.
5. События называются независимыми если:
1)Они не могут произойти одновременно.
2)Если оба события являются невозможными.
3)Если на вероятность появления одного из них не влияет появление или непоявление другого.
4)Если справедливо соотношение P(AB)=P(A)P(B).
5)Если верно P(AB)=P(A).
6. Обычная монета брошена 10 раз. И все 10 раз выпал орел.Что случится при 11 броске?
1) Выпадет орел.
2) Вероятнее всего решка.
3) Равновозможно и орел и решка.
4) Обязательно решка.
7. Требуется вычислить вероятность того, что 10 раз выпадет орел.
1) p=
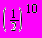 2)
2) 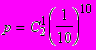 3)
3) 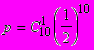 4)
4) 
8. Формула Пуассона
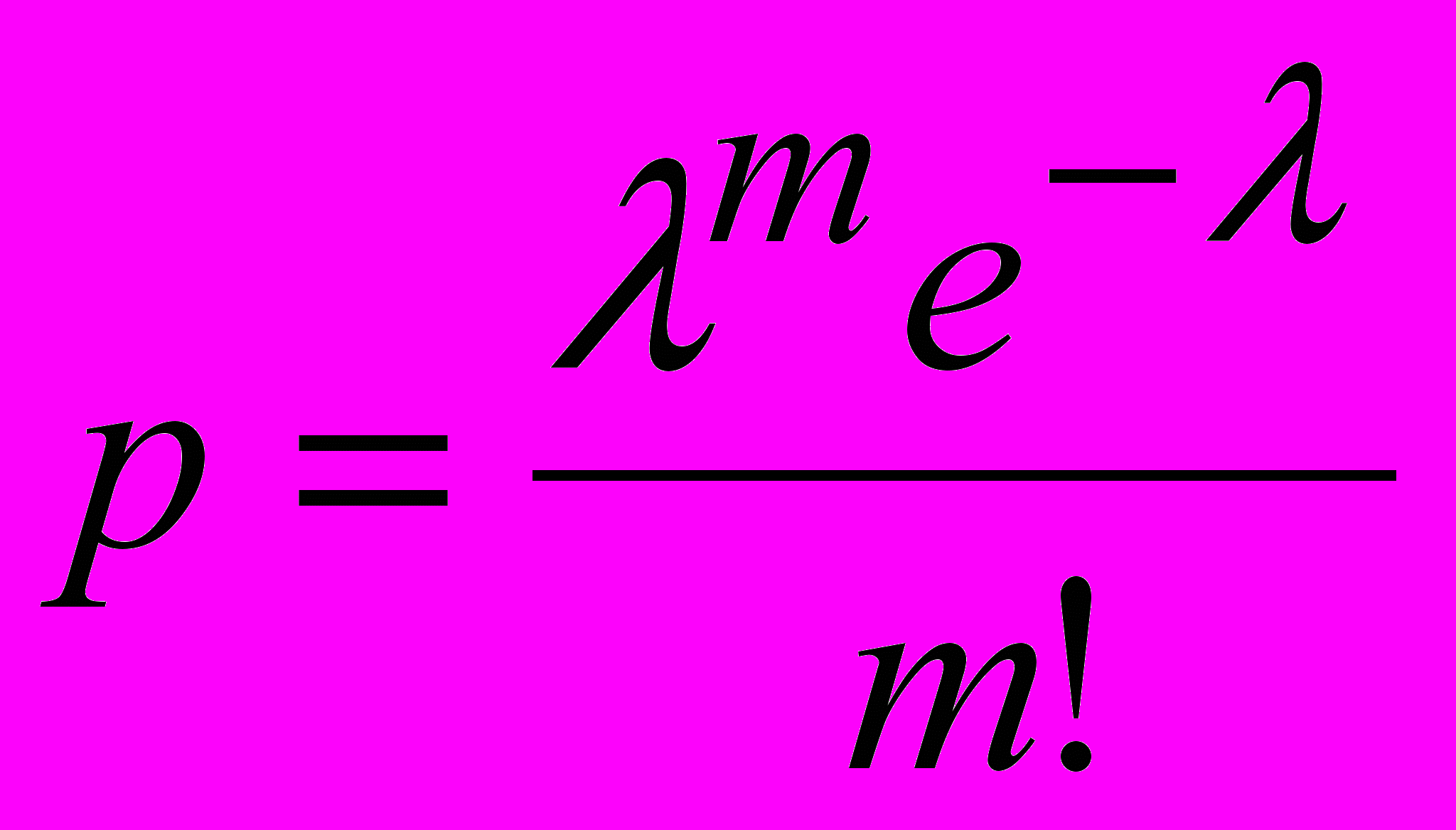 .
.1)Дает приближенное значение вероятности m успехов при n испытаниях в случае n и p<0.1.
2)Дает вероятность того, что при n испытаниях успех повторится m раз подряд.
3) Дает приближенное значение вероятности , вычисленное по формуле Бернулли при большом числе испытаний и малой вероятности успеха.
4) Дает приближенное значение вероятности
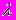 успехов при m испытаниях.
успехов при m испытаниях.- Телефонная станция обслуживает 1000 абонентов. Вероятность телефонного вызова в течение часа для одного абонента составляет p=0,005. Вычислить при помощи таблиц вероятность того, что в течение часа позвонят 10 абонентов.
P= ? (ваш ответ)
- Формула Лапласа применяется для :
1) вычисления вероятности лапласовских событий.
- вычисления вероятности очень редких событий.
- вычисления вероятности почти достоверных событий.
- приближенного вычисления вероятности по формуле Пуассона при малом числе испытаний .
- приближенного вычисления вероятности по формуле Бернулли при большом числе испытаний
11. Студент знает 10 из 30 билетов. Вычислить вероятность того, что он сдаст экзамен, если известно, что к моменту его прихода перед ним прошло 8 человек , из которых трое вытянули известные ему билеты.
- 10/30 ; 2) 1/3; 3) 2/22; 4) 7/22; 5) 2/27;
- Вычислить вероятность сдачи экзамена при тех же изначальных знаниях студента (см. 11), но при условии, что студенту удастся занять очередь пораньше и он зайдет вторым.
1)1/3; 2)2/3; 3)10/29; 4)нет верных ответов .
Часть 2
13. Нормальное распределение задается плотностью вероятности:
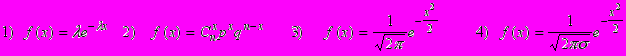
 14. Дано равномерное на отрезке (1; 4) распределение Высота h при этом будет равна: y 1) 1; 2)2; 3)1/2; 4)1/3; 5)1/4;
14. Дано равномерное на отрезке (1; 4) распределение Высота h при этом будет равна: y 1) 1; 2)2; 3)1/2; 4)1/3; 5)1/4;


 h
h

 1 4 x
1 4 x 15. Для проверки зависимости двух случайных величин X и Y необходимо
1) Вычислить MX, MY и сравнить их с 0.
- Вычислить DX, DY и сравнить их между собой .
- Вычислить ковариацию и сравнить ее с 0 .
16. По закону распределения двух случайных величин вычислен коэффициент корреляции r=0,98. Из этого следует, что:
1)Величины независимы .
2)Величины зависимы функционально.
3) Величины зависимы статистически с сильно выраженной линейной зависимостью
- Величины зависимы статистически с сильно выраженной нелинейной зависимостью .
17. По закону распределения двух случайных величин связанных соотношением Y=
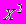 вычислен коэффициент корреляции r .Его значение должно быть :
вычислен коэффициент корреляции r .Его значение должно быть :- близко к 0;
- близко к +1 или -1 ;
- каким угодно .
18. По закону распределения двух случайных величин вычислен коэффициент корреляции r=1. Из этого следует, что:
1) Величины независимы .
2) Величины зависимы функционально.
3) Величины зависимы статистически с сильно выраженной линейной зависимостью
4) Величины зависимы статистически с сильно выраженной нелинейной зависимостью
5) Величины линейно зависимы
- Дан закон распределения случайной величины X :




 x 1 2 3
x 1 2 3 p 0.2 0.3 0.5 Вычислите MX :
p 0.2 0.3 0.5 Вычислите MX :1) 1.5 2) 2 3)3 4)2.3 5)3.1
20. Выделите неверные свойства:
1) M(X+Y)=MX+MY; 2) D(X+Y)=D(X)+D(Y) ; 3) M(CX)=CMX;
- D(CX)=CDX; 5) M(XY)=MX MY ; при независимости X и Y ;
6) D(XY)=D X DY ;при независимости X и Y ;
21. Задайте закон распределения случайной величины: число выпавших орлов при трехкратном бросании монеты.
| 1 | x | 0 | 1 |
| | p | 0,5 | 0,5 |
| 2 | x | 0 | 1 | 2 |
| | p | 0,5 | 0,25 | 0,25 |
| 3 | x | 1 | 2 | 3 |
| | p | 0,25 | 0,5 | 0,25 |
| 4 | x | 0 | 1 | 2 | 3 |
| | p | 1/8 | 3/8 | 3/8 | 1/8 |
22. Случайная величина рост человека нормально распределена с параметрами среднее значение 172, дисперсия 100. Сколько человек имеют рост от 167 до 182 см в группе из 400 человек?
1)162; 2) 244 3) 177; 4) 213
