Методические рекомендации Екатеринбург 2009 удк ббк о
| Вид материала | Методические рекомендации |
| 6.5. Реализация внутрипредметных связей Задача. Дана правильная призма ABCA 6.7. Включение историко-математического материала 6.8 Организация контроля знаний учащихся |
- Методические рекомендации Екатеринбург 2006 удк 025. 32 (075. 5) Ббк ч 736., 523.58kb.
- Методические рекомендации Иркутск 2005 ббк удк, 1679.51kb.
- Методические рекомендации г. Пермь 2009 удк 373. 5 Ббк 74. 24(2) Н83 Издание подготовлено, 2317.64kb.
- Методические рекомендации Томск 2009 ббк 73. 3(0)я73 Печатается по решению, 928.69kb.
- Методические рекомендации Ярославль 2005 удк 338. 24; 338. 26; 338. 27 Печатается, 579.59kb.
- Методические рекомендации уфа 2010 удк 636 ббк 45., 880.28kb.
- Методические рекомендации соискателям ученых степеней Оренбург-2005 удк 01(076., 493.32kb.
- Материалы международной студенческой научной конференции 21 апреля 2009 г г. Екатеринбург,, 2547.76kb.
- Методические рекомендации Гродно 2007 удк 37. 018 Ббк 373., 358.38kb.
- Методические рекомендации Минск, 2007 удк ббк, 357.83kb.
6.5. Реализация внутрипредметных связей
Реализация внутрипредметных связей в обучающей деятельности учителя заключается в отборе материала, который представляет эти связи, в выборе организационных форм, методов и приемов обучения, направленных на наиболее успешное усвоение этого материала.
При реализации внутрипредметных связей в процессе обучения следует учитывать тот факт, что связи могут быть логико-математического и методического характера.
Логико-математические связи – это необходимые глубокие связи, вытекающие из логики и содержания учебного предмета; на их основе строится изучение материала.
Методические связи выполняют чисто дидактические функции, они приводятся с целью иллюстрации, сравнения, сопоставления и т.д. Эти связи реализуются учителем в процессе адаптации учебного материала к индивидуальным и возрастным особенностям учащихся.
В рамках отчетности необходимо проиллюстрировать внутрипредметные связи логико-математического характера.
Реализацию внутрипредметных связей логико-математического характера можно представить в виде схемы, или проиллюстрировать на задачном материале.
Для иллюстрации логико-математических связей на задачном материале, необходимо:
1. Выделить основные виды задач, решаемые в данной теме.
2. Выбрать одну из задач и проиллюстрировать на ее примере реализацию внутрипредметных логико-математических связей.
Пример логико-математических связей понятия «квадратный трехчлен» (рис. 1).
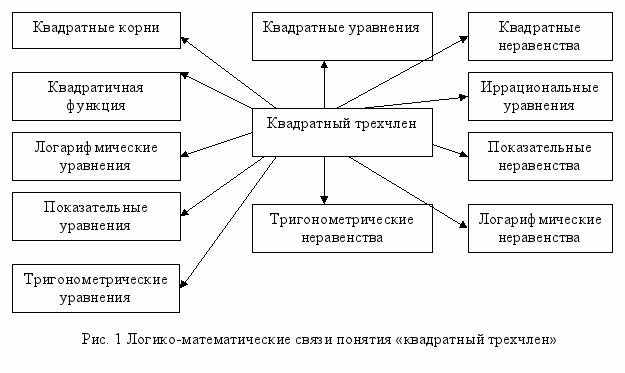 Пример реализации внутрипредметных логико-математических связей при изучении темы: «Перпендикулярность прямых и плоскостей»
Пример реализации внутрипредметных логико-математических связей при изучении темы: «Перпендикулярность прямых и плоскостей»При изучении этой темы решаются следующие задачи: на использование признаков перпендикулярности прямой и плоскости; на построение прямой перпендикулярной плоскости; на нахождение угла между прямой и плоскостью; на построение плоскости перпендикулярной данной прямой; на построение плоскости перпендикулярной другой плоскости; на построение отрезка равного расстоянию от точки до плоскости; на нахождение расстояния между скрещивающимися прямыми и.т.
Решение всех этих задач, требует умения правильно строить чертеж фигуры и ее элементов. Все элементы пространственной фигуры связаны между собой какими–то соотношениями, умение их найти, выразить неизвестные величины через, возможно, одну-единственную известную величину, требует установления внутрипредметных связей логико-математического характера.
Например:
Реализация внутрипредметных связей логико-математического характера при решении задачи на нахождение расстояния между прямой и плоскостью.
Чтобы ответить на вопросы задач, на нахождение расстояния между прямыми и плоскостями, надо уметь пользоваться свойствами прямых и плоскостей в пространстве, свойствами фигур на плоскости, знать тригонометрические формулы и уметь ими пользоваться, решать квадратные уравнения и многое другое.
Задача.
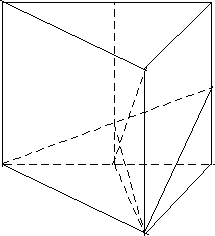
Дана правильная призма ABCA1B1C1D1. D и С2 – середины ребер ВС и СС1, АВ = АА1 = а. Найдите расстояние до точки пересечения прямой A1D с плоскостью АВС2 от точки А1 (рис. 2).
При решении данной задачи на этапе построения точки P включаются следующие внутрипредметные логико-математические связи из курса стереометрии: свойство правильной призмы, свойства параллельных плоскостей, построение линии пересечения двух плоскостей. При нахождении расстояния А1Р включаются внутрипредметные связи из курса планиметрии – свойства подобных треугольников, свойство средней линии треугольника, теорема Пифагора
Решение. Так как призма правильная, то в основании лежит правильный треугольник и она прямая. Построим точку пересечения прямой A1D с плоскостью АВС2. С этой целью построим вспомогательное сечение призмы какой-нибудь плоскостью, проходящей через прямую A1D. Эта плоскость пересекает верхнее основание призмы по прямой А1DAD (по свойству параллельных плоскостей), линией пересечения этого сечения AА1D1D и плоскости ABC2 является AD2, D1D ВС2 = D2. Тогда А1D и AD2 лежат в одной плоскости и А1D AD2 = P. Точка P искомая.
Отрезок А1Р, длина которого искомая, включен в треугольник АА1Р. при этом ясно, что DD1AA1. тогда треугольник АА1Р DD2P, тогда
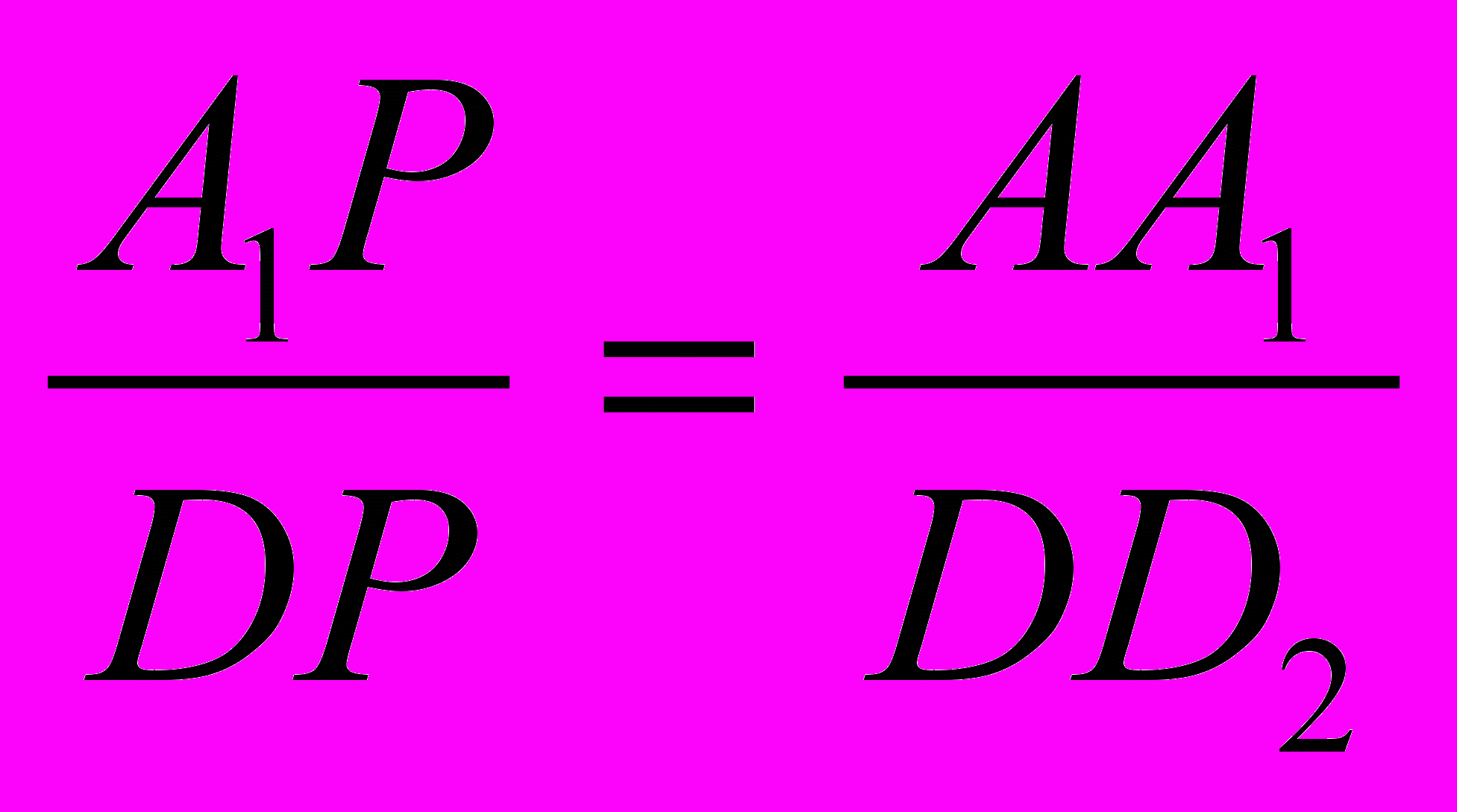 . Так как АА1 = а и DD2 – средняя линия треугольника ВСС2. То есть
. Так как АА1 = а и DD2 – средняя линия треугольника ВСС2. То есть 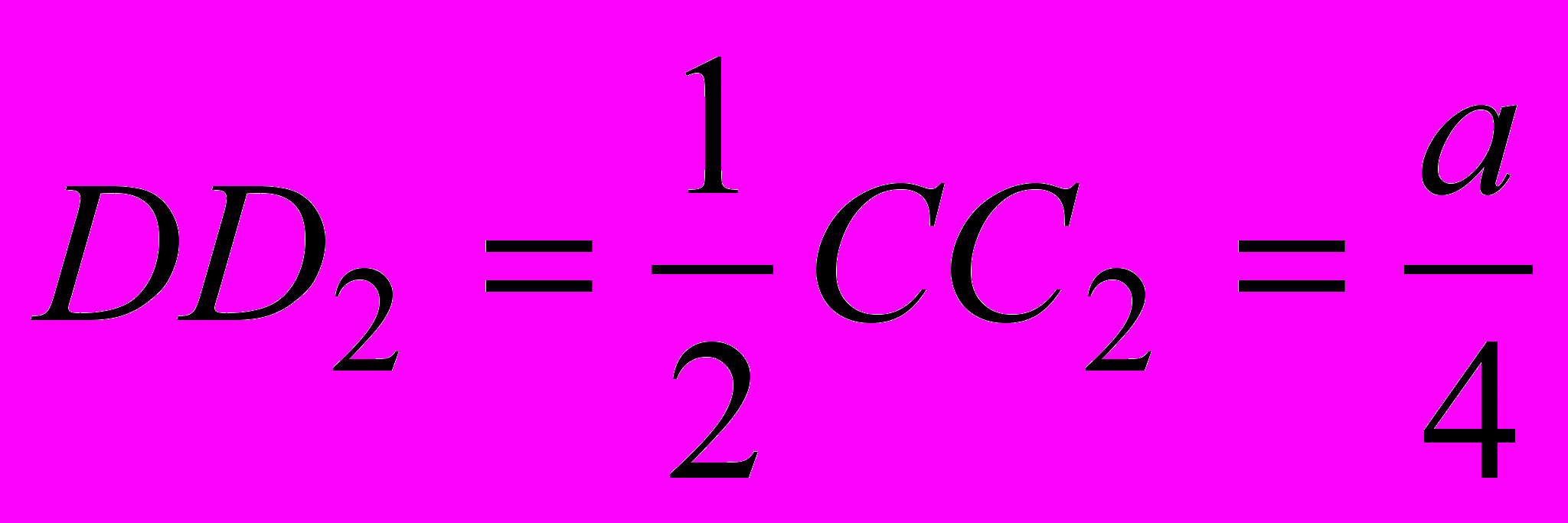 , то
, то 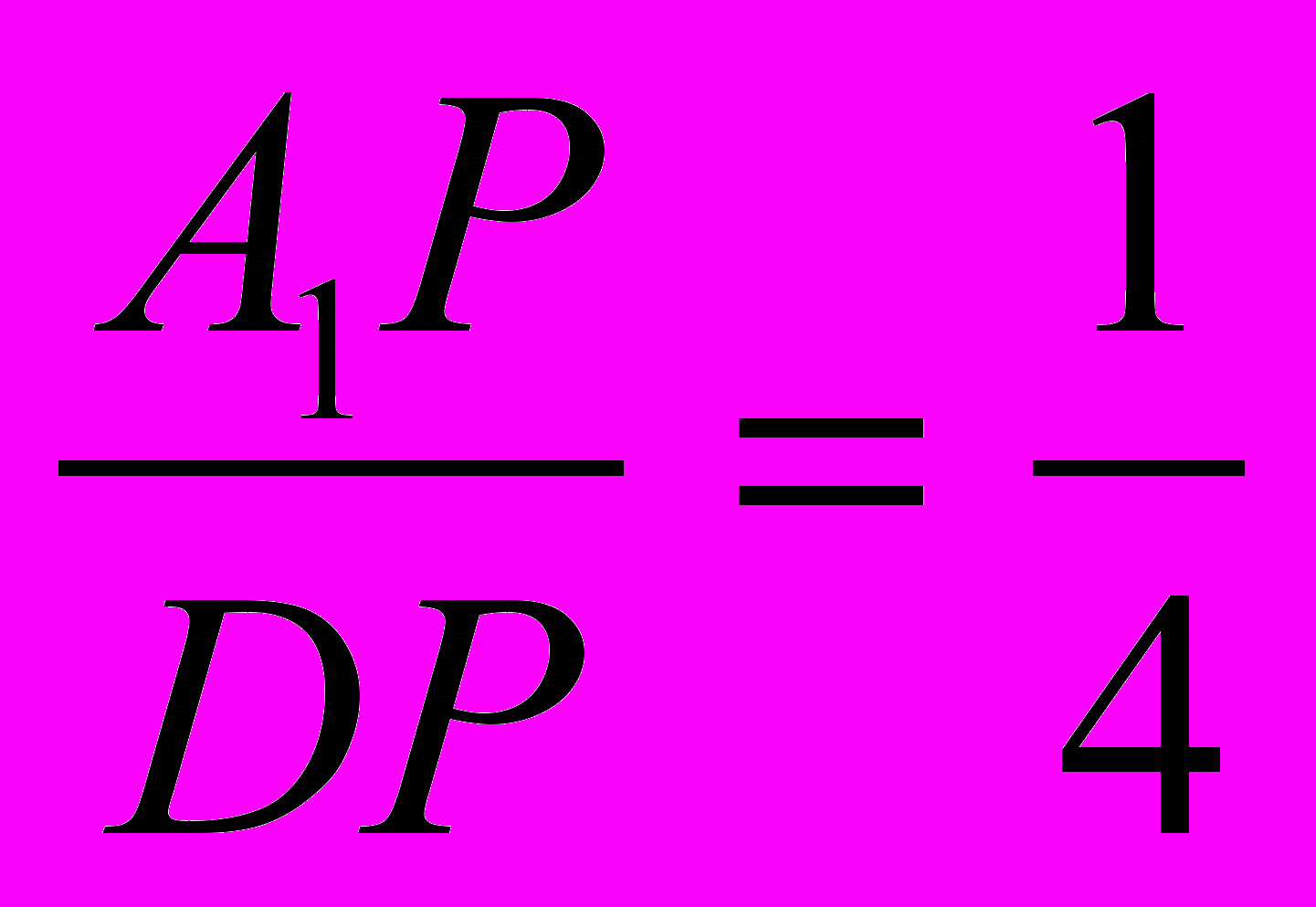 .
.B
 1 D1 C1
1 D1 C1 A1
C2
D2
P
B D C
A
Рис. 2.
Тогда А1Р:А1D = 4:5, из прямоугольного треугольника А1АD
 . В итоге получим А1Р =
. В итоге получим А1Р = 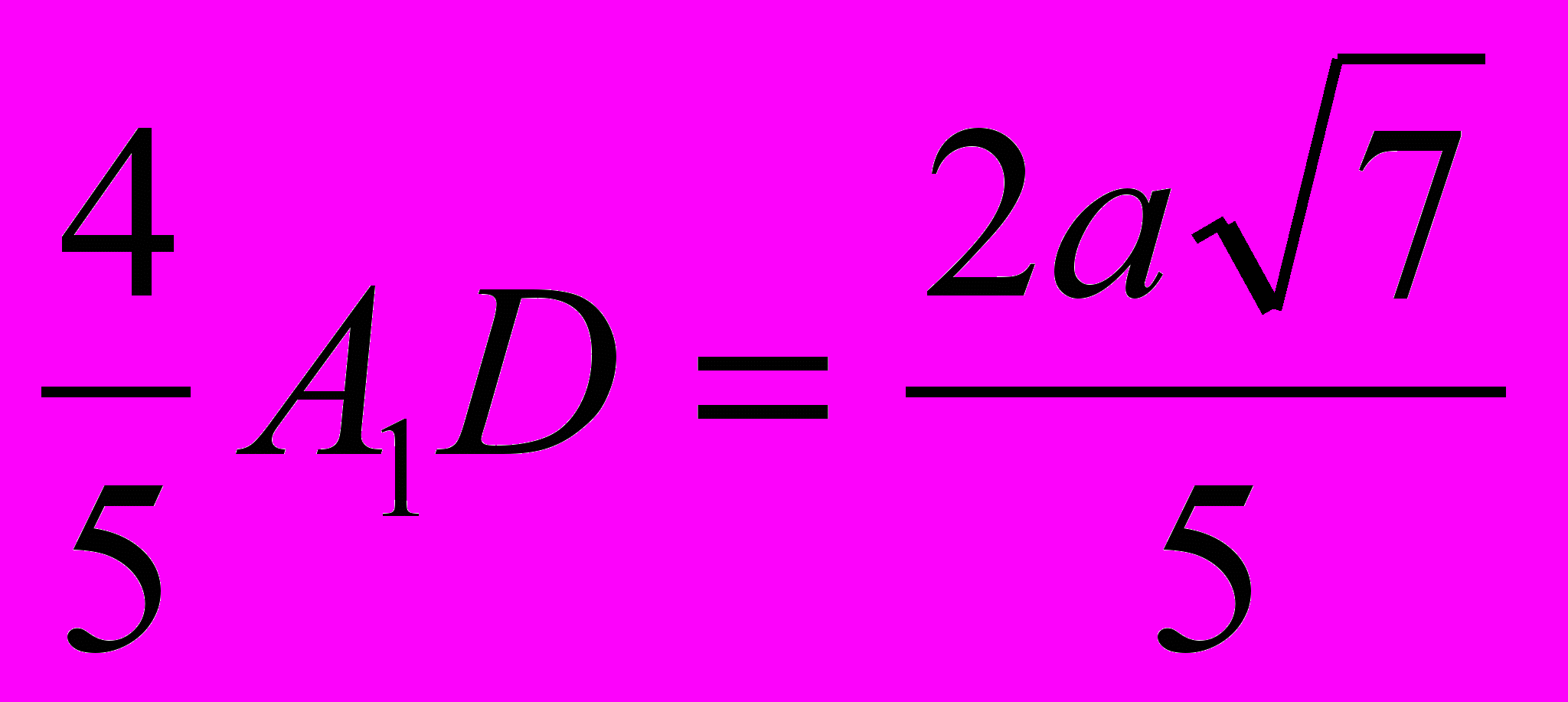 . Что и требовалось вычислить.
. Что и требовалось вычислить.6.6. Реализация межпредметных связей
Содержание данного компонента логико-дидактического анализа предполагает разработку дидактических материалов межпредметного характера и рекомендаций по их применению в процессе обучения математике.
В процессе обучения математике для реализации межпредметных связей могут применяться самые разнообразные методы. Наиболее распространенные из них: информационно-рецептивный, проблемный, исследовательский, программный, эвристический. Средства подбираются учителем в соответствии с содержанием каждого конкретного урока. Это могут быть вопросы, задания, задачи, тексты, наглядные пособия, проблемные ситуации, познавательные задачи и т.д.
Например, межпредмтные связи могут реализовываться в вопросах межпредметного содержания, проблемных вопросах межпредметного характера, домашнем задании, межпредметных контрольных работах, межпредметных практических работах, наглядных комплексных пособиях, кроссвордах межпредметного содержания.
Общая схема тематического планирования реализации межпредметных связей может быть представлена в виде таблицы (табл. 1).
Таблица 1
| Темы и даты уроков | Основные предметные понятия и умения | Связь с другими предметами | Методы и приемы обучения | Наглядные пособия | Задания с включением межпредметных связей | ||
| | | Смежные понятия | Факты | Умения | | | |
6.7. Включение историко-математического материала
При введении элементов историзма в школьный курс математики нужно исходить из следующих положений:
- Включение элементов историзма в курс математики должно осуществляться в соответствии с целью и задачами образовательного процесса и содержанием изучаемого материала.
- Необходимо демонстрировать учащимся взаимосвязь развития математики как науки с практической деятельностью людей на протяжении многих веков. Под влиянием требований других наук и техники математика была вынуждена решать новые проблемы, создавать новые методы решения задач, которые обогатили и саму математику.
- При использовании элементов историзма в процессе обучения математике необходимо применять различные формы и виды организации деятельности школьников, способствующие активизации познавательного интереса учащихся, создавать проблемные ситуации.
В данном разделе логико-дидактического анализа темы должны быть представлены:
- Перечень основных вопросов истории, связанных с изучаемой темой.
- Форма включения историко-математического материала в процесс изучения темы.
Пример включения историко-математического материала при изучении темы «Квадратные уравнения»
При изучении данной темы может быть рассмотрен следующий перечень вопросов:
- квадратные уравнения в Древнем Вавилоне;
- как составлял и решал Диофант квадратные уравнения;
- квадратные уравнения в Индии;
- квадратные уравнения у ал-Хорезми;
- квадратные уравнения в Европе XVIII – XVII;
- о теореме Виета.
Материал может быть представлен учащимися в форме доклада, реферата. Для решения в процессе изучения темы могут быть использованы следующие задания:
1. Решить следующие квадратные уравнения из «Арифметики» Диофанта:
 ;
; 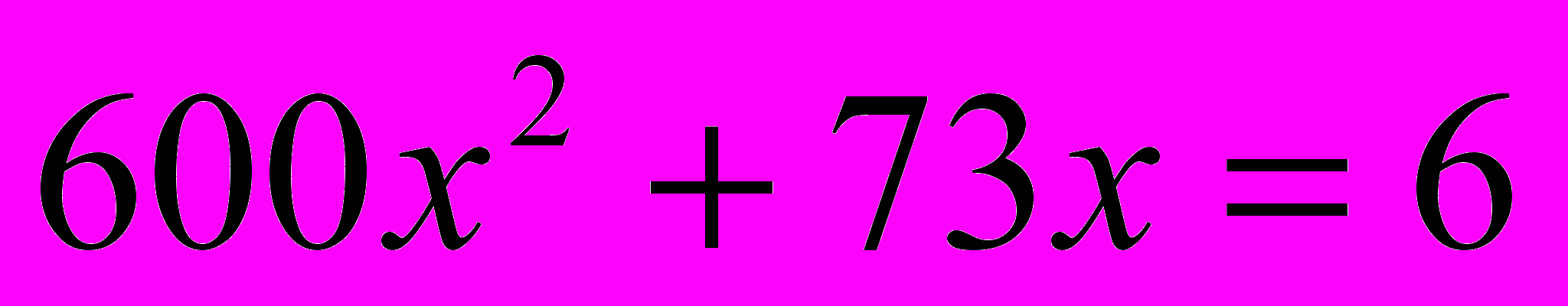
2. Реши задачу способом Бхаскары:
«Обезьянок резвых стая… А двенадцать по лианам
Всласть поевши, развлекалась Стали прыгать повисая
Их в квадрате часть восьмая Сколько ж было обезьянок,
На поляне забавлялась. Ты скажи мне в этой стае?»
6.8 Организация контроля знаний учащихся
Контроль означает выявление, измерение и оценивание знаний, умений обучаемых.
По содержанию контроль бывает предварительный, текущий, тематический, итоговый. Предварительный контроль фиксирует исходный уровень обученности. Текущий контроль позволяет диагностировать степень усвоения учебного материала. В тематическом контроле проверяется усвоение каждым учащимся конкретной темы. Итоговый контроль позволяет выявить соответствие уровня подготовки учащихся требованиям программы.
При проведении предварительного контроля целесообразно использовать следующие формы: фронтальную беседу; подготовительную самостоятельную работу; тест, выявляющий общую подготовку класса к изучаемой теме. Для проведения фронтальной беседы учителю необходимо составить перечень вопросов, направленных на выявление уровня актуальной обученности.
Текущий контроль может осуществляться в форме тренировочной индивидуальной самостоятельной работы; обучающей индивидуальной и групповой самостоятельной работы; проверочной самостоятельной работы; проверки домашнего задания.
Для проведения тематического контроля эффективно использовать следующие формы: закрепляющую самостоятельную индивидуальную работу, позволяющую определить прочность усвоения материала, фронтальную беседу, тест, контрольную работу.
Итоговый контроль может быть организован в форме конференции, зачета, экзамена.
Пример организации контроля знаний учащихся по теме «Элементы тригонометрии»
Так как, учащиеся уже знакомы с определением синуса, косинуса и тангенса острого угла прямоугольного треугольника, с основным тригонометрическим тождеством и формулами приведения из курса геометрии, а также работали с единичной полуокружностью, то при проведении предварительного контроля важно выяснить исходный уровень обученности. Это можно сделать в форме фронтальной беседы.
Перечень вопросов для фронтальной беседы:
- Что такое единичная полуокружность?
- Что называется синусом угла
 ?
?
- Что называется косинусом угла
 ?
?
- Что называется тангенсом угла
 ?
?
Какие тригонометрические формулы вам известны?
Для успешного изучения данной темы, также очень важно, чтобы учащиеся хорошо ориентировались при работе с тригонометрическим кругом, могли быстро показать точку на единичной окружности, соответствующую углу поворота (особенно табличные углы).
Вопросы и задания могут быть следующие:
1) отметить точку на единичной окружности, соответствующую данному углу поворота (например:
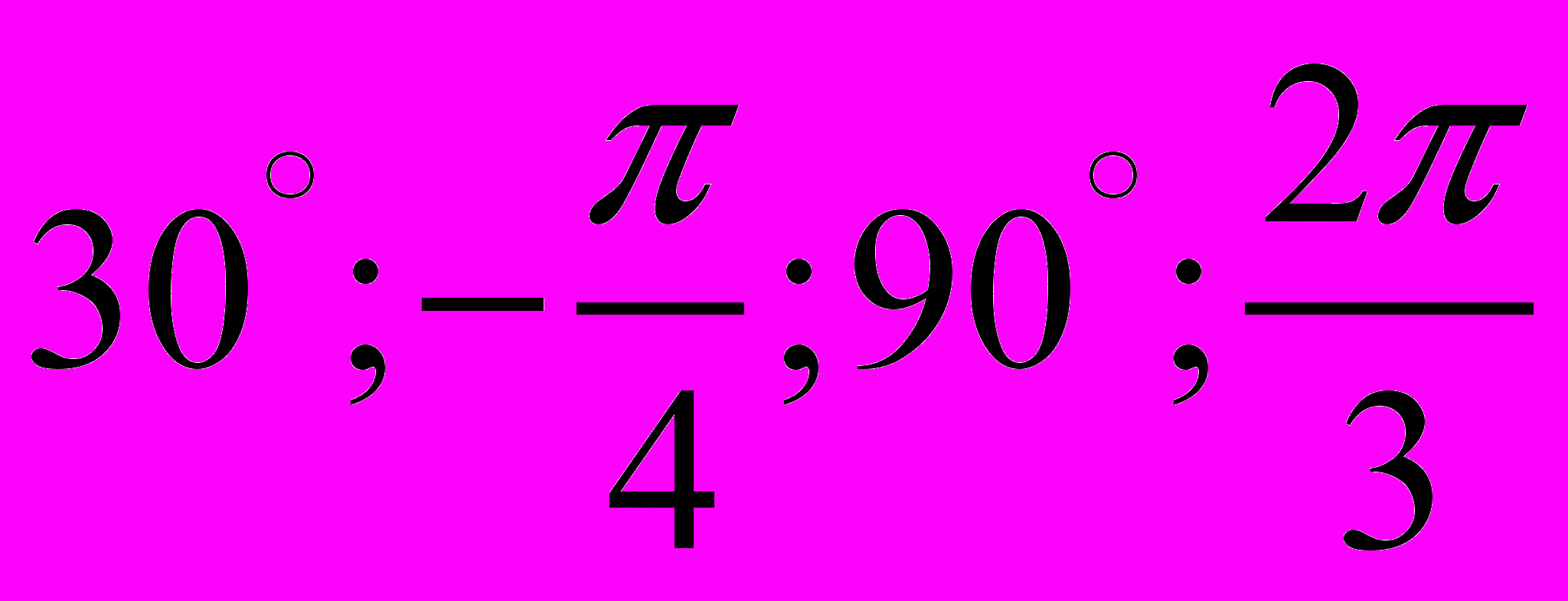 и т.д.);
и т.д.);2) перевести градусную меру угла в радианную и наоборот
(например:
 );
);3) в какой четверти располагается угол
 .
.(например:
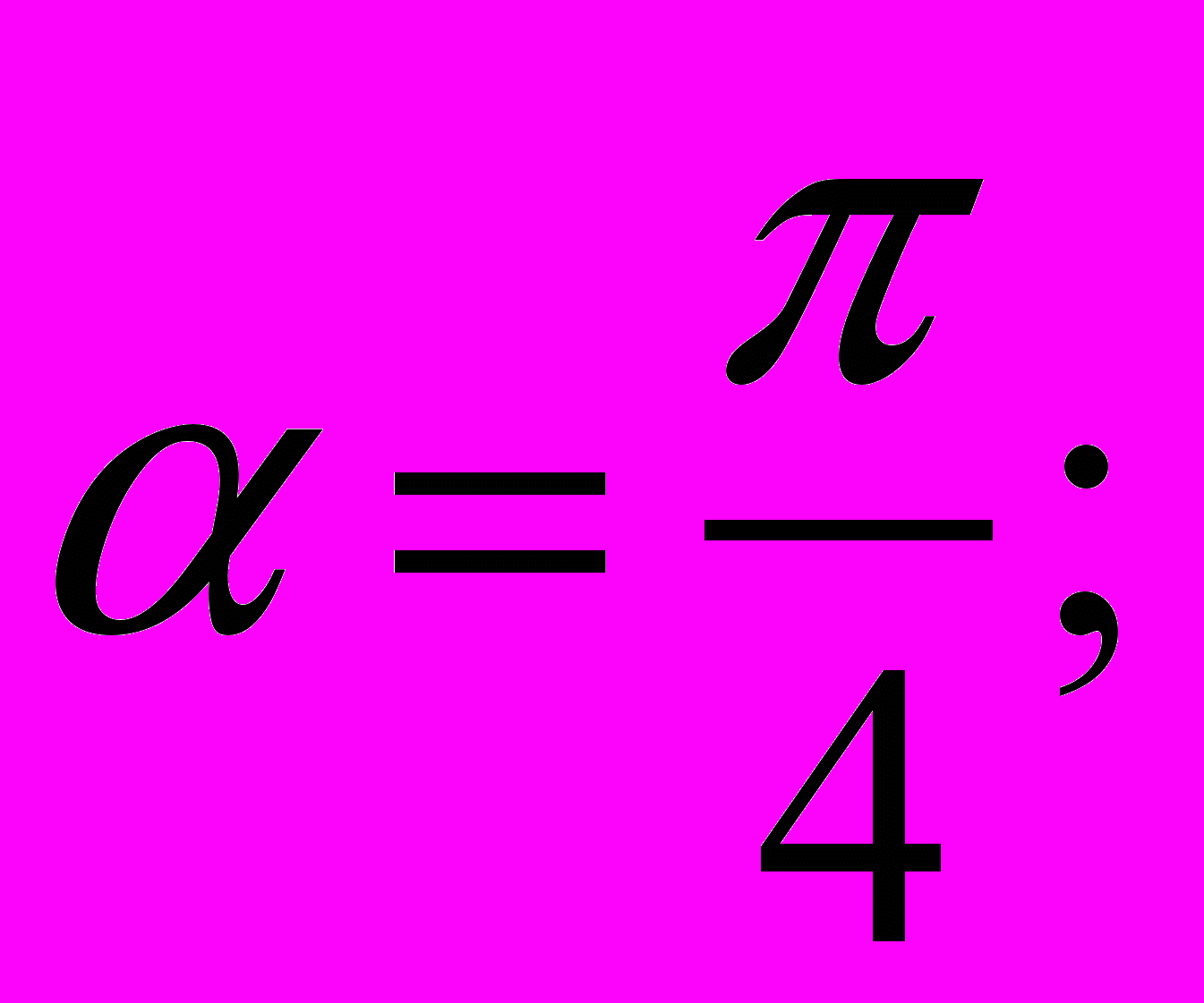
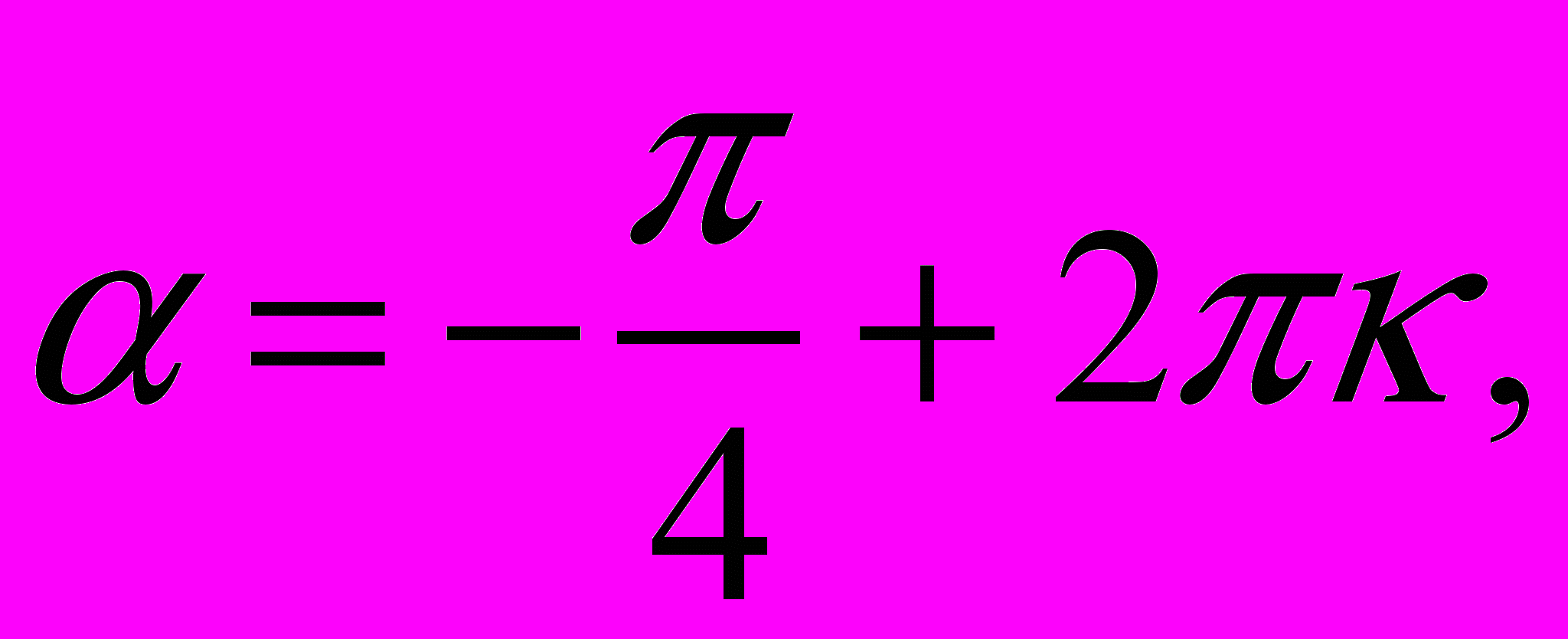
 ).
).Пример организации текущего контроля
После введения определений синуса, косинуса и тангенса произвольного угла целесообразно провести обучающую самостоятельную работу.
Цель работы: проверить понимание учениками содержание определений данных понятий.
В соответствии с поставленной целью в эту работу включаются задания, при выполнении которых ученики столкнутся с необходимостью «проговорить» определения синуса и косинуса угла, что очень важно для его понимания. Кроме того, для проверки степени усвоения материала целесообразно дать задание, в котором среди множества выражений ученик должен выбрать верные равенства.
Например:
Задания:
1. Вставьте пропущенные слова так, чтобы получилось истинное высказывание:
-
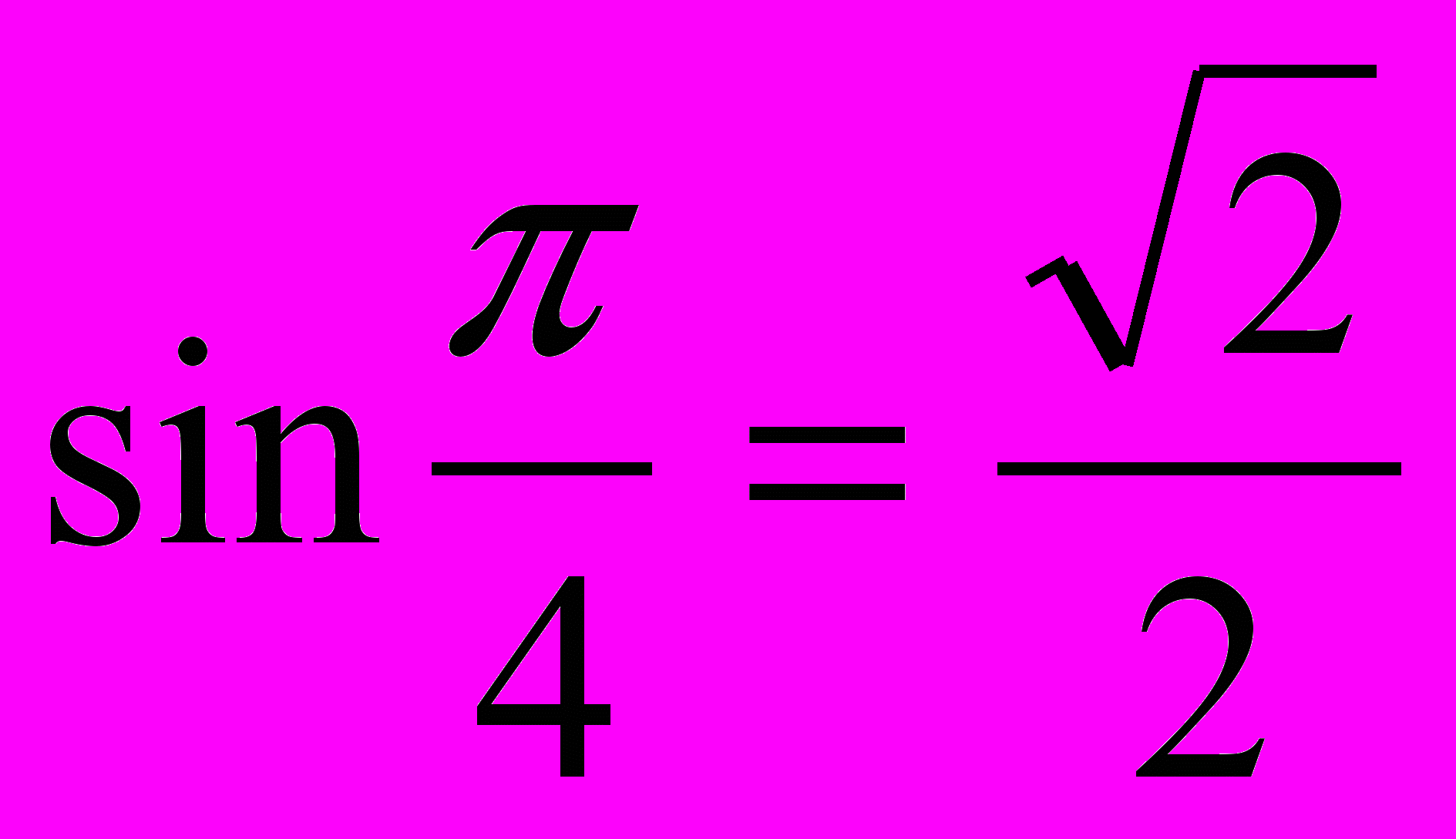 , так как при повороте точки (1;0) на угол получается точка с координатами …, а ордината этой точки равна ….
, так как при повороте точки (1;0) на угол получается точка с координатами …, а ордината этой точки равна ….
-
 , так как при повороте точки (1;0) на угол …, получается точка с координатами …, а абсцисса этой точки равна ….
, так как при повороте точки (1;0) на угол …, получается точка с координатами …, а абсцисса этой точки равна ….
- Точка (1;0) при повороте на угол 3 перейдет в точку с координатами …, поэтому sin 3 равен …

cos 3 равен …
2. Какие из следующих равенств являются верными:
-
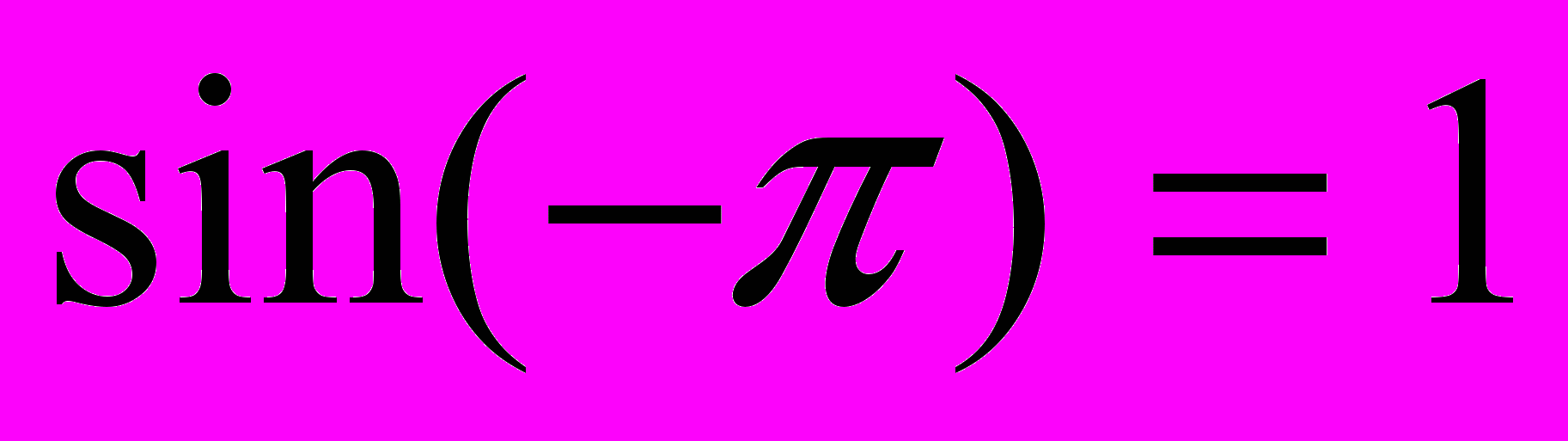 d)
d) 
-
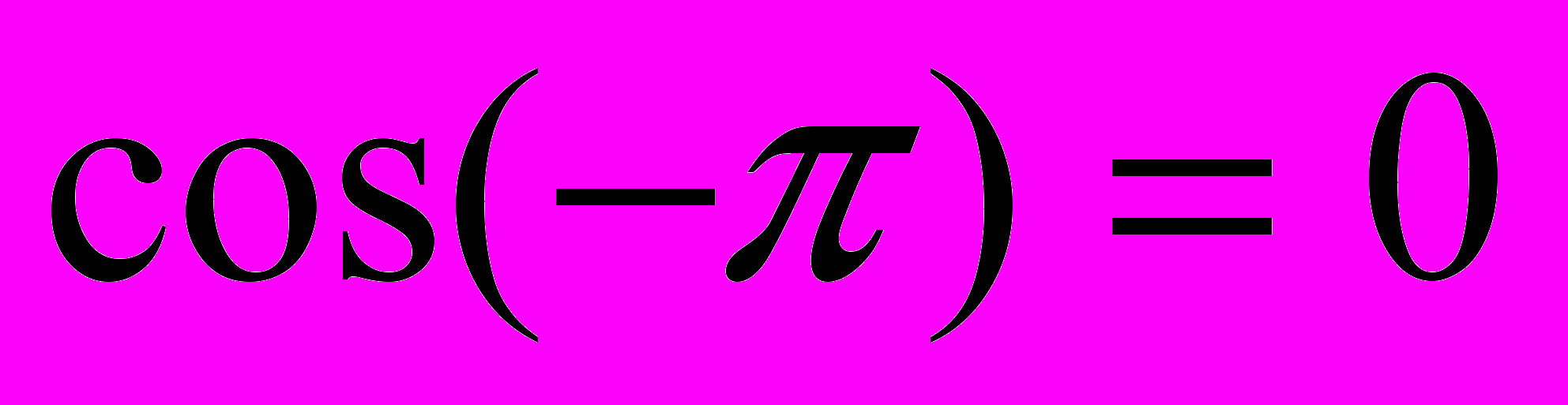 e)
e) 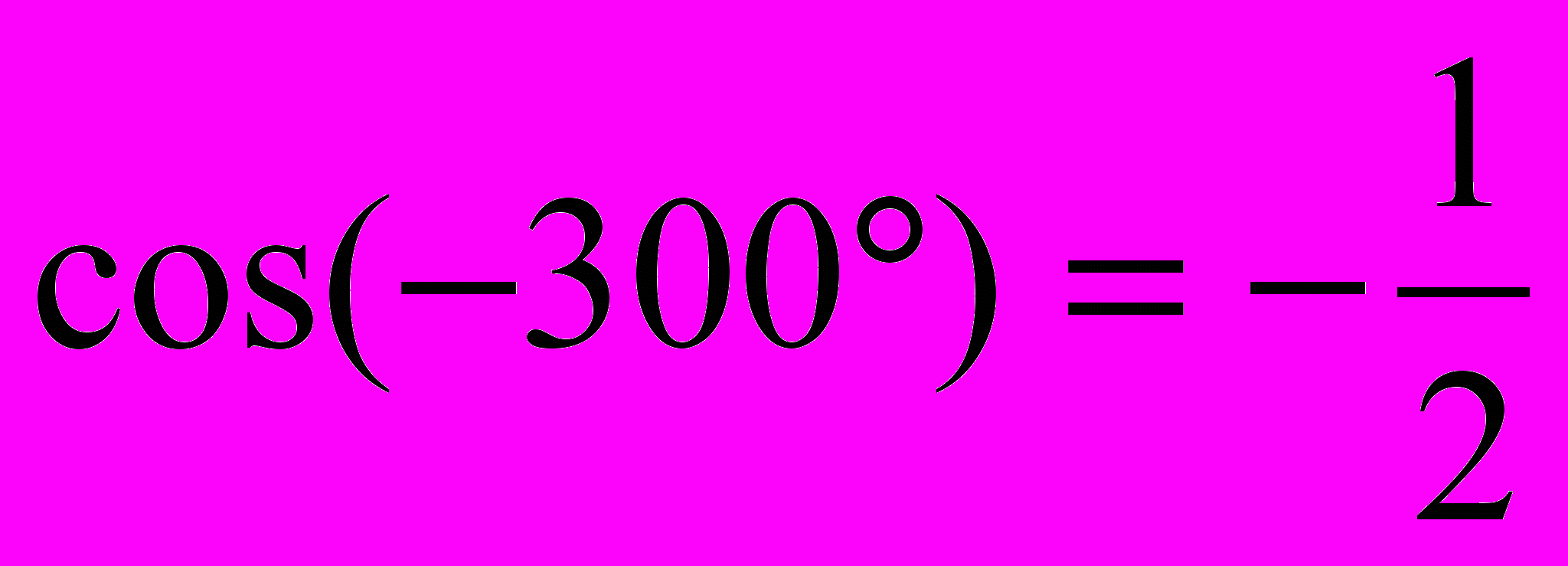
-
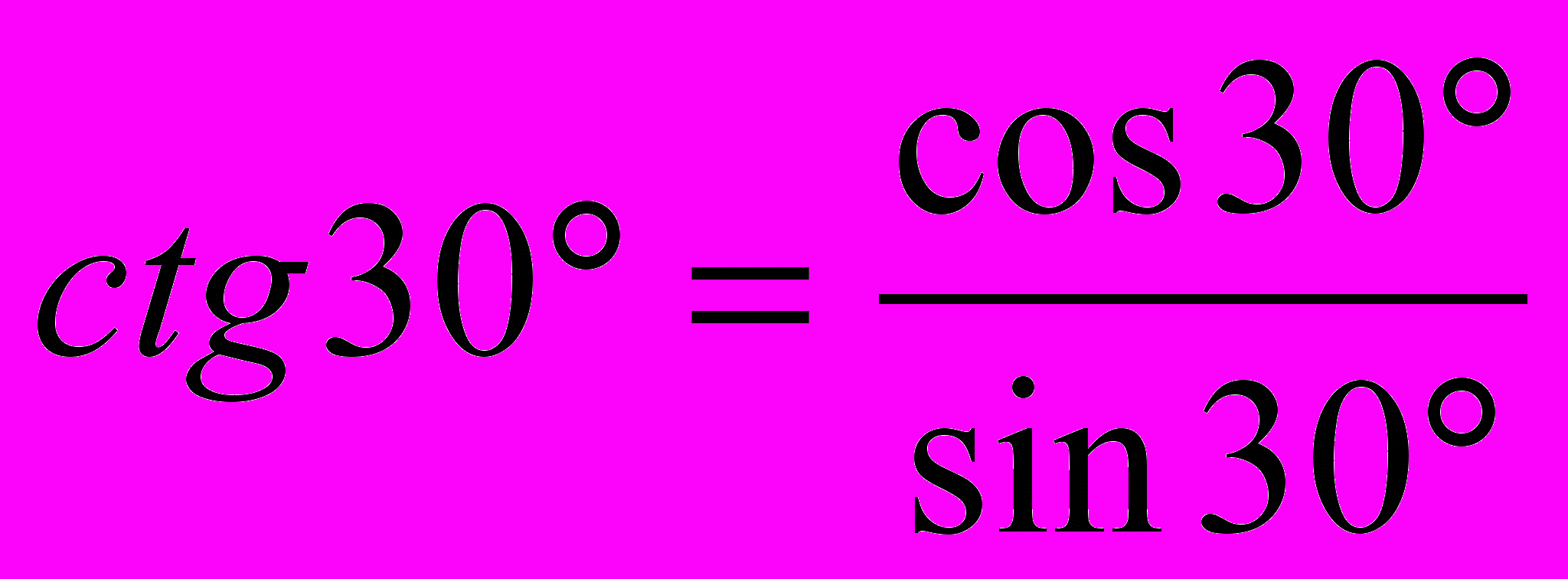 f)
f) 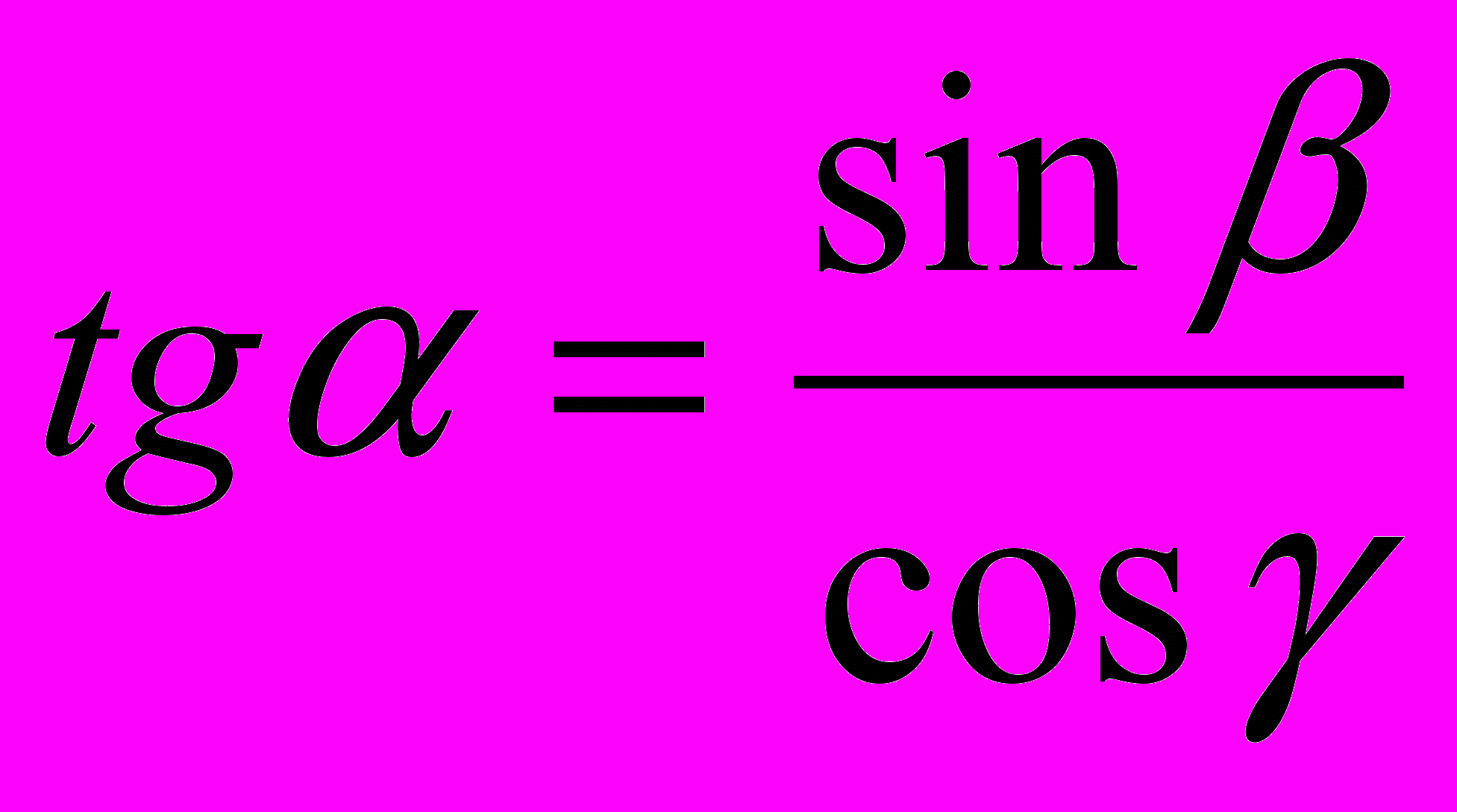
На втором уроке необходимо провести работу, цель которой: проверить умения учащихся применять при решении задачного материала определения синуса, косинуса, тангенса и котангенса.
Например:
Вариант I.
- Вычислить:
-
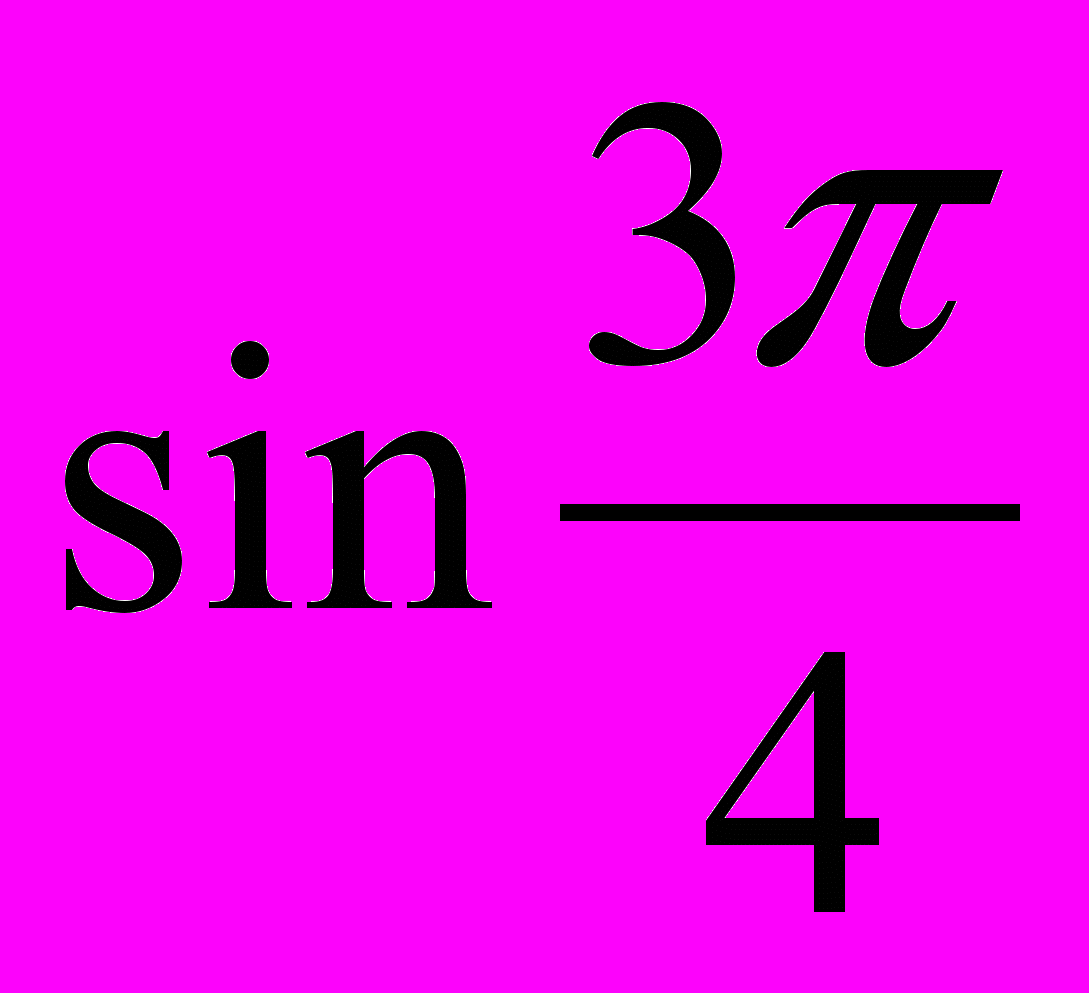 b)
b) 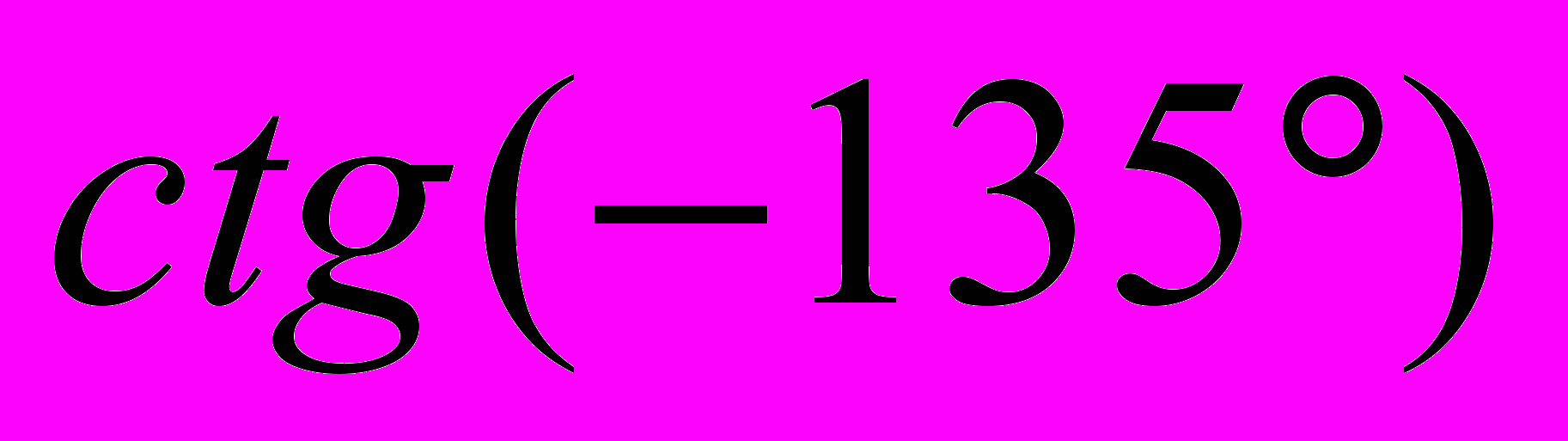 c)
c) 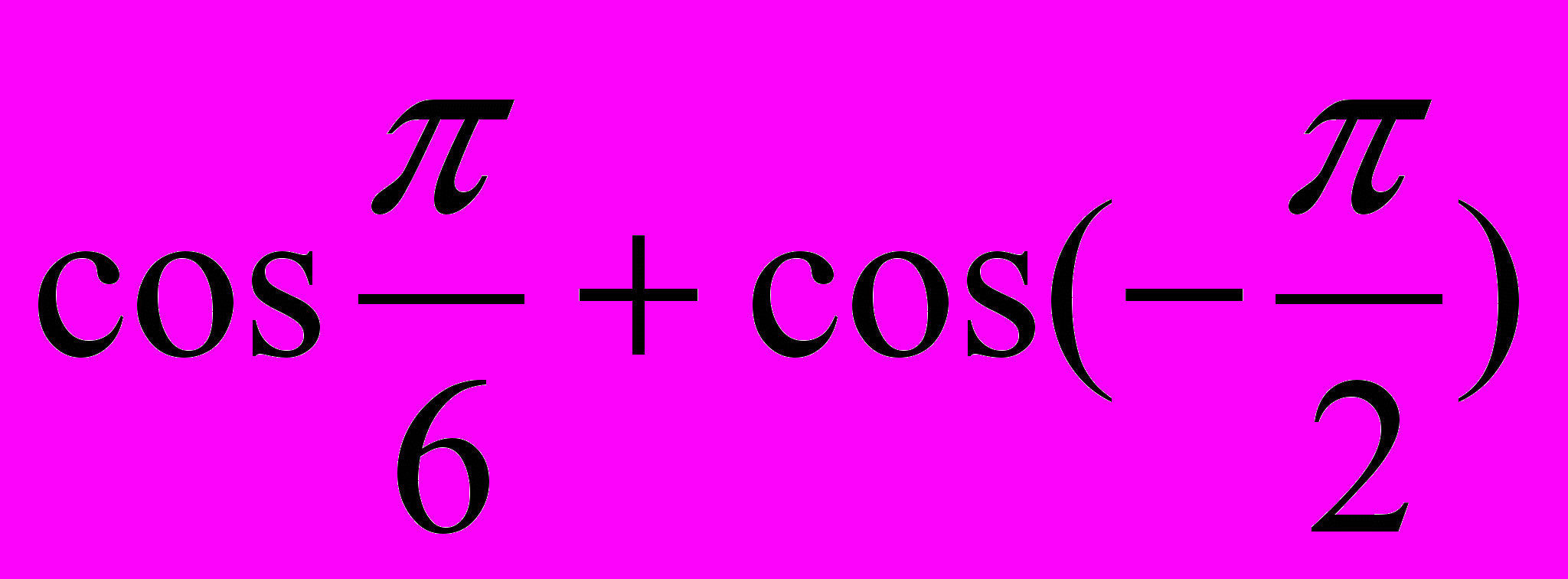
-
2) Изобразить на единичной окружности точки, соответствующие углу
 , если
, еслиa)
 b)
b) 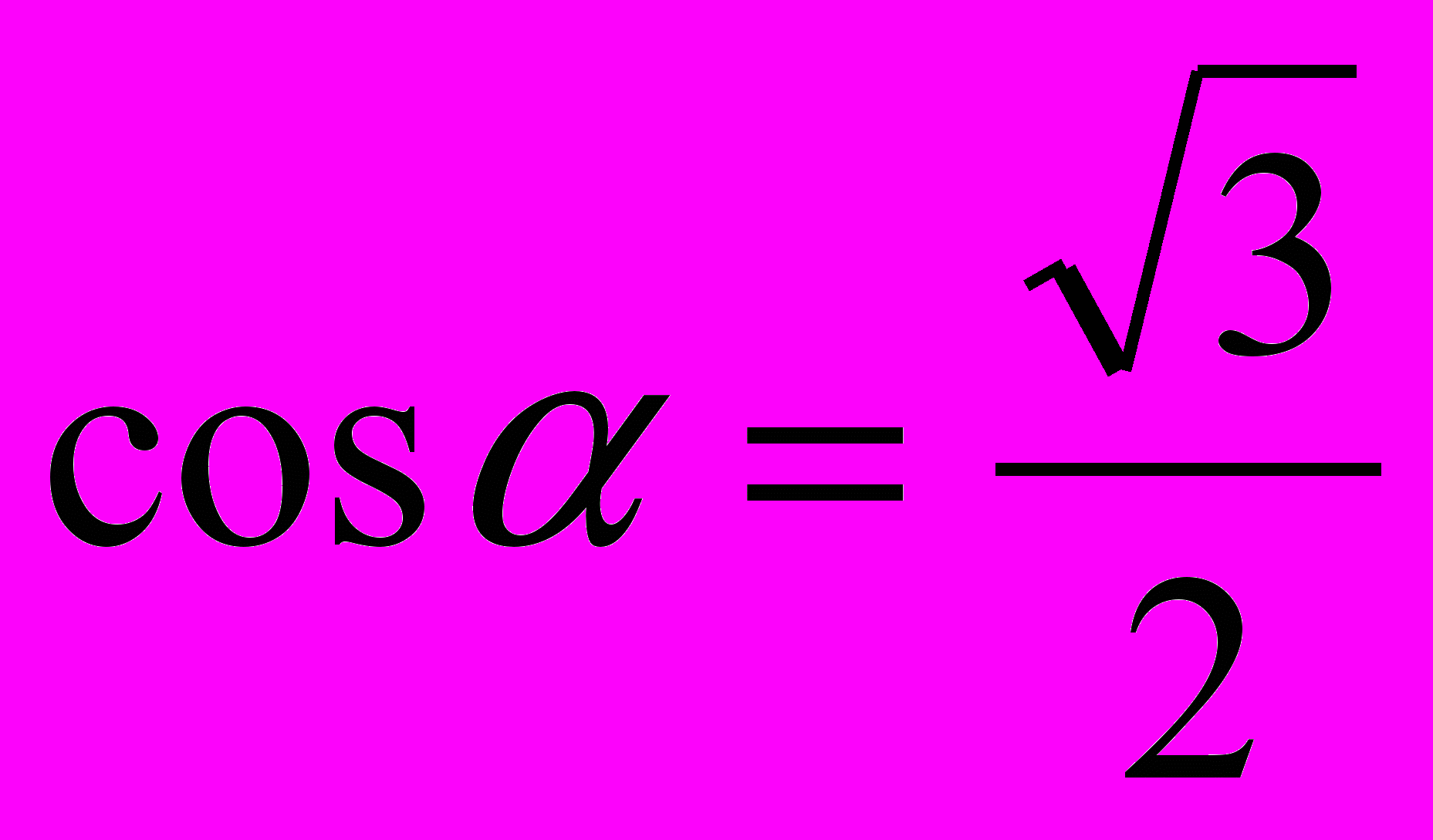
3) Решить уравнение: cos x - 1= 0
При вычислении значений тригонометрических функций одного и того же аргумента по данному значению одной из функций, у многих учащихся вызывает затруднения определения знака перед корнем в использовании основных тригонометрических тождеств. Поэтому целесообразно перед изучением темы “Зависимость между синусом, косинусом и тангенсом одного и того же угла” в начале урока провести фронтальный опрос, в котором необходимо повторить, как определяются знаки значений тригонометрических функций с целью облегчения восприятия и понимания нового материала школьников.
Вопросы могут быть следующие:
- Дать определение синуса угла; косинуса угла; тангенса угла.
- В какой четверти располагается угол (назвать границы)
a) =
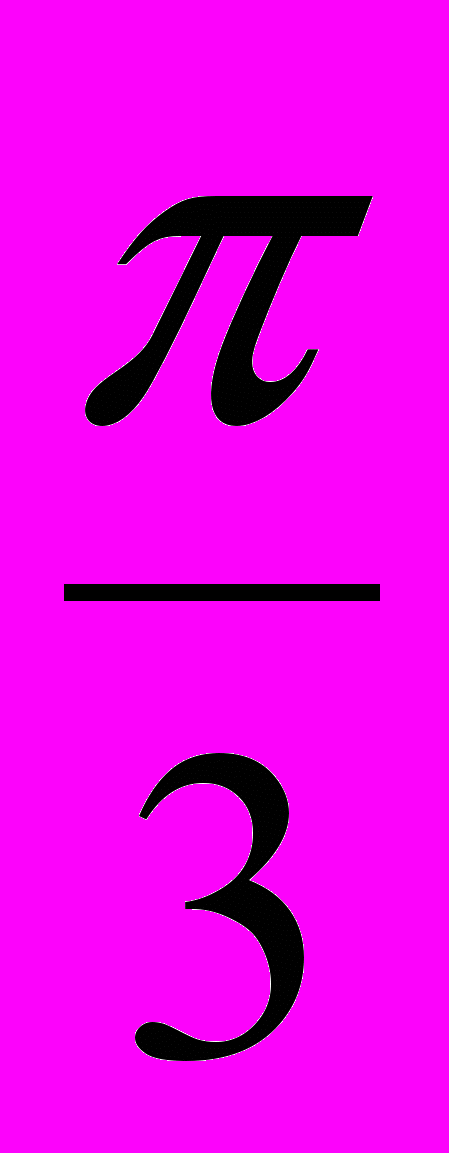


b)

c) =3
- Определить знак числа: sin
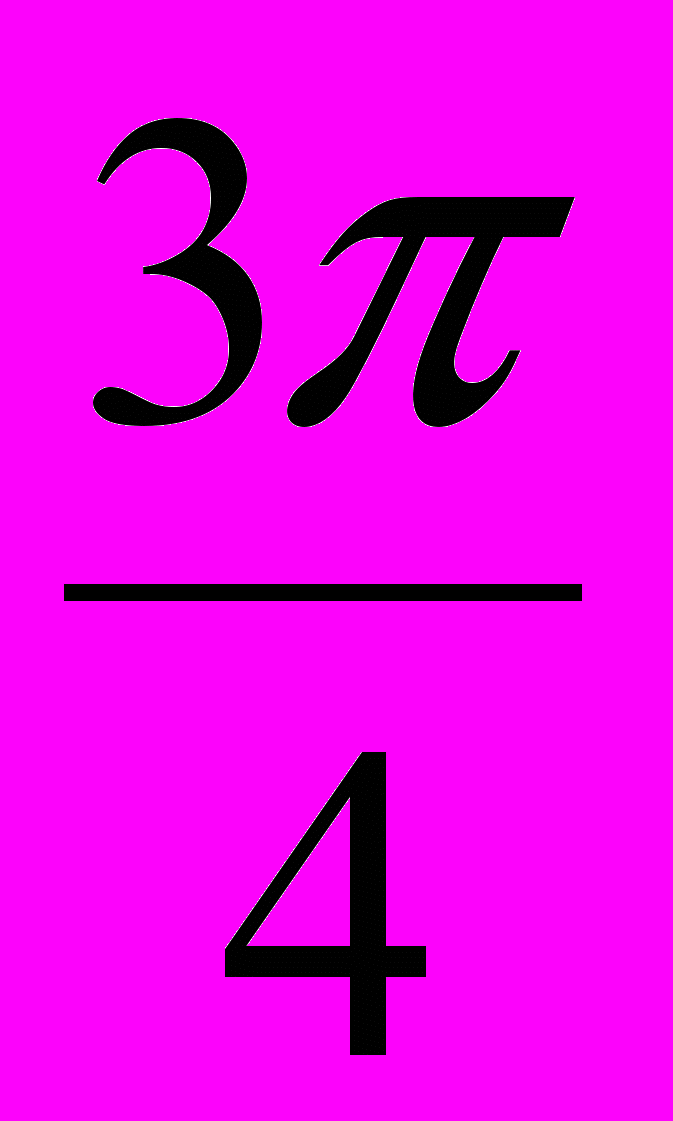 ; cos (-
; cos (-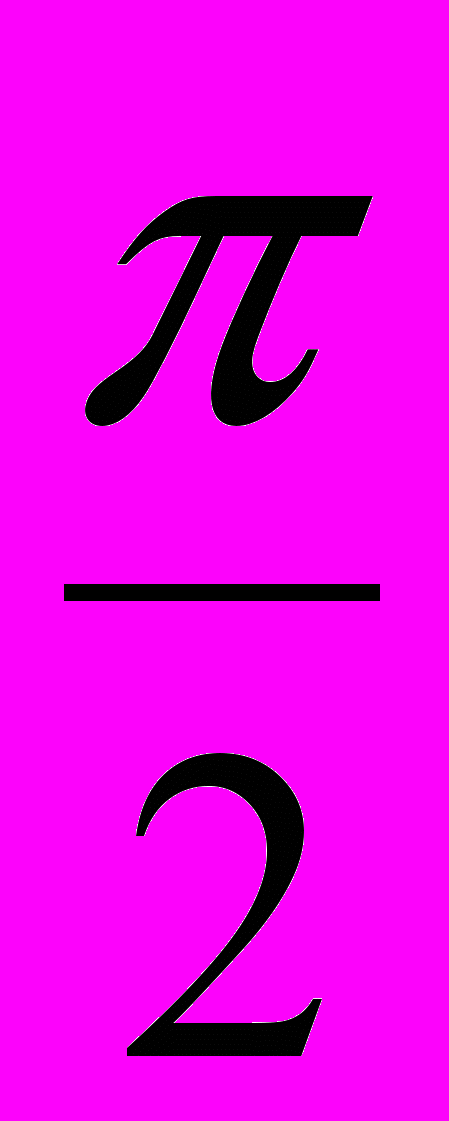 ); sin
); sin 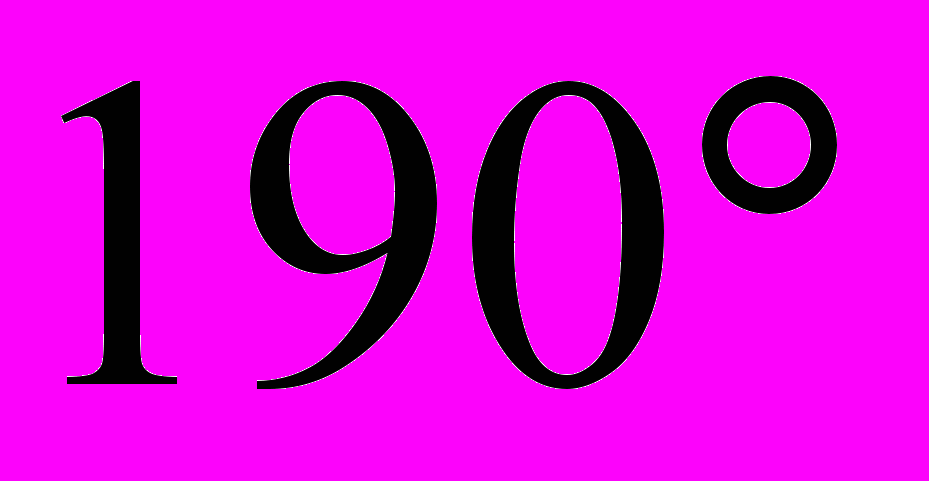 ; cos
; cos 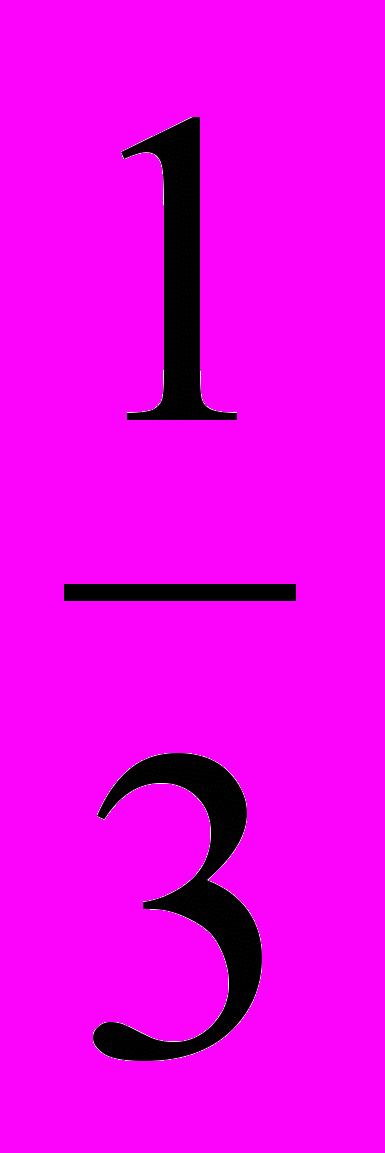 ; tg 6.
; tg 6.
- В какой четверти может быть расположен угол, если его косинус- число отрицательное.
Проводя повторение, учитель ставит вопрос и после некоторой паузы вызывает учащегося для ответа, а затем в случае необходимости, других –для исправлений и дополнений. В конце учитель подводит итоги, выставляет учащимся отметки.
Пример проверочной работы по теме: «Тригонометрические функции двойного аргумента»
Цель работы: проверить умения учащихся применять формулы тригонометрических функций двойного аргумента для вычисления выражений и при решение уравнений.
В соответствии с поставленной целью задания могут быть следующие.
Вариант I.
- Вычислить:
-
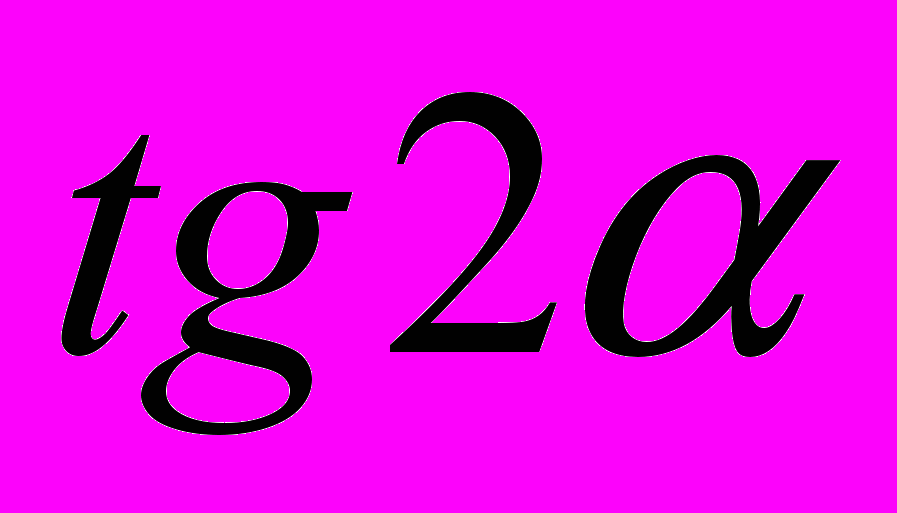 , если
, если 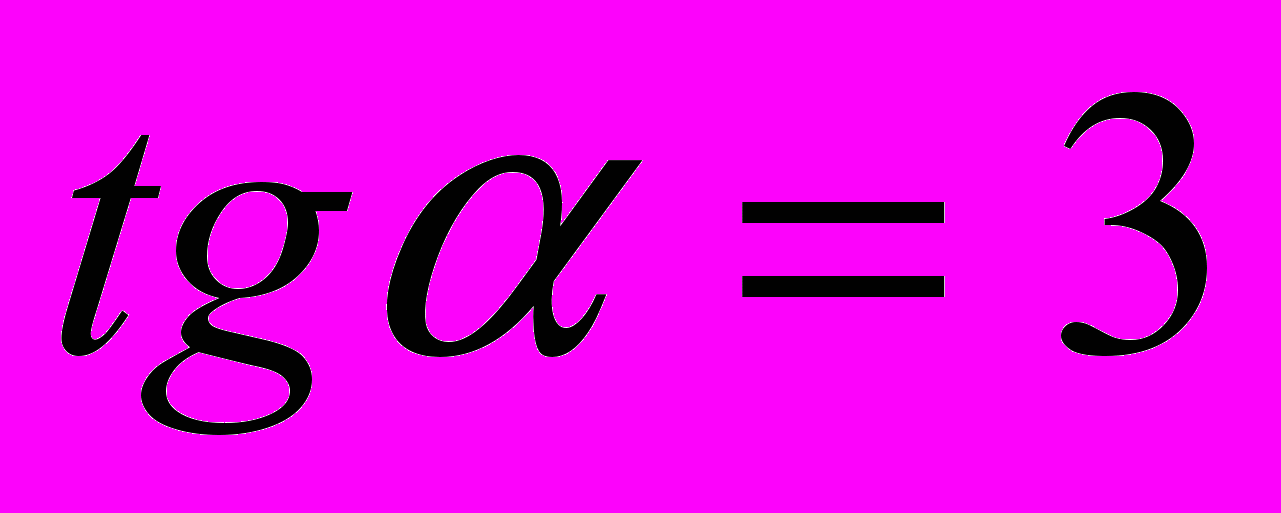 ;
;
-
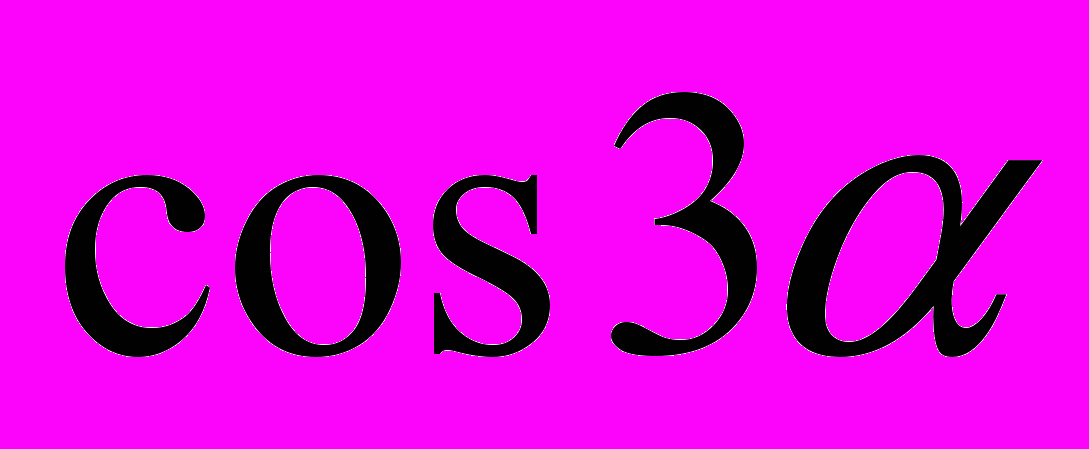 , если
, если 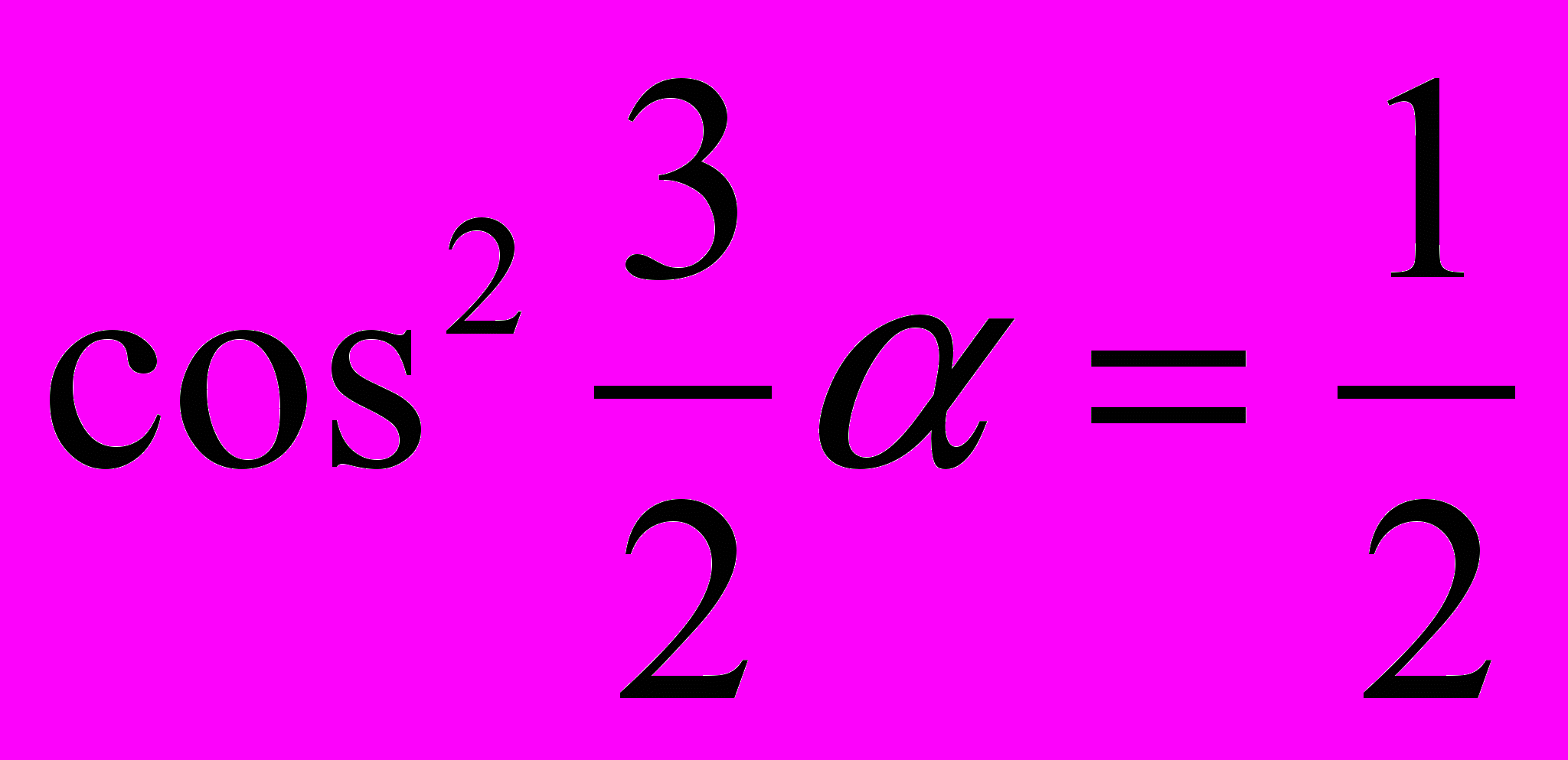
-
2. Решить уравнение: 1 -
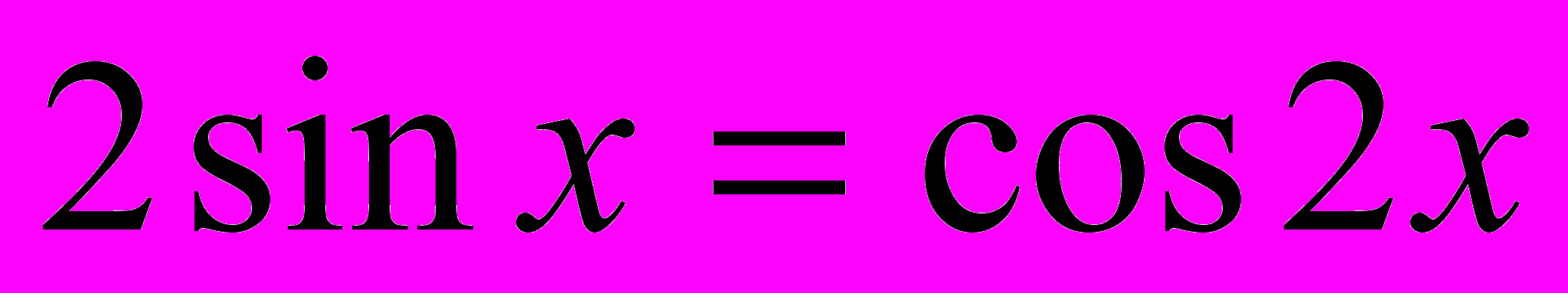 .
.Пример проверочной работе по теме: «Формулы сложения».
Форма работы: индивидуальная работа учащихся по карточкам.
Цель работы: проверить умения учащихся применять формулы сложения при выполнении преобразований тригонометрических выражений.
Приведем несколько вариантов карточек.
К – 1 К - 2
1. Вычислить
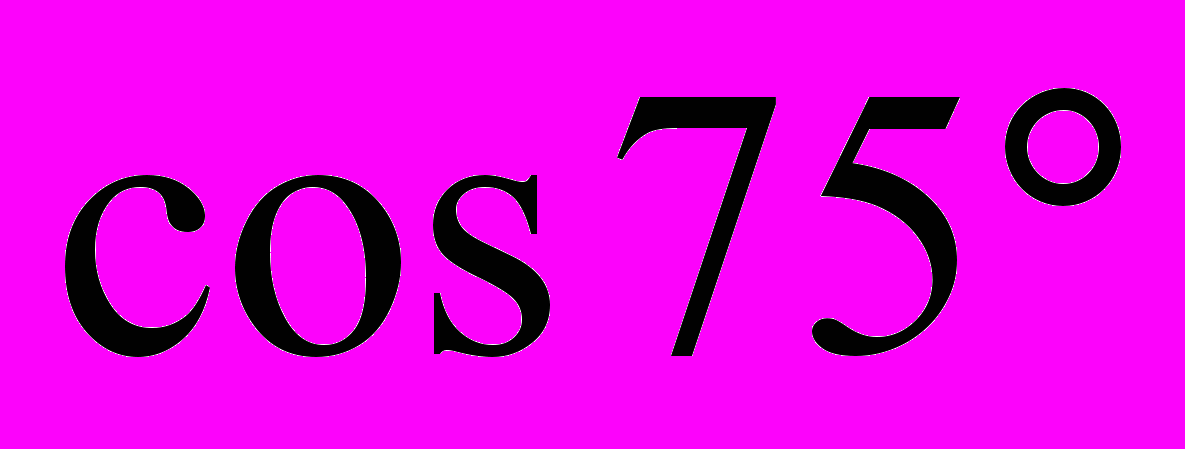 1. Вычислить
1. Вычислить 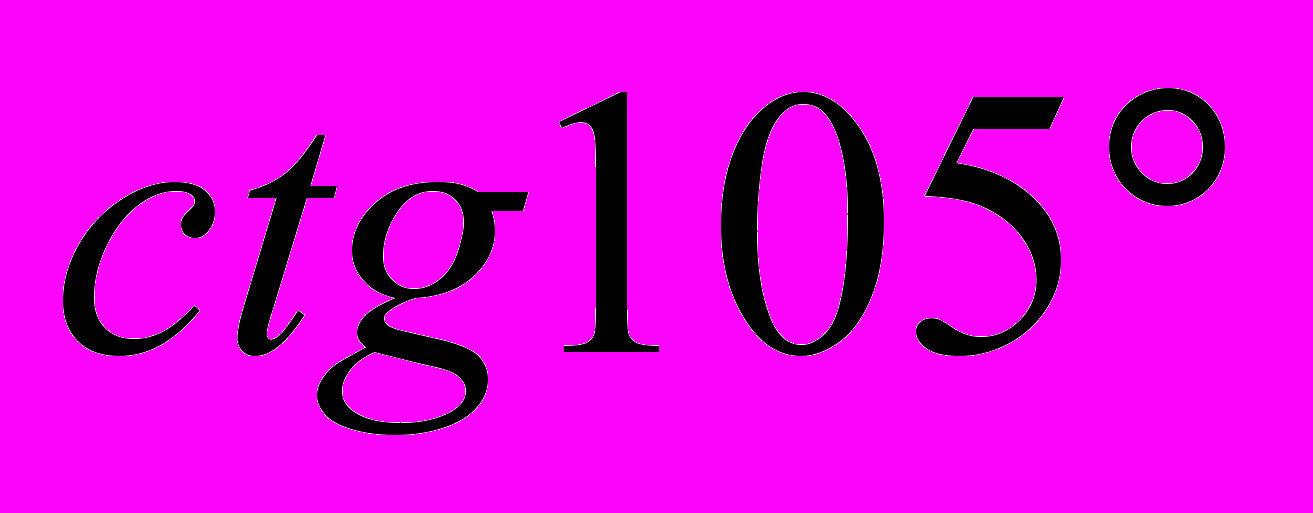
2. a)
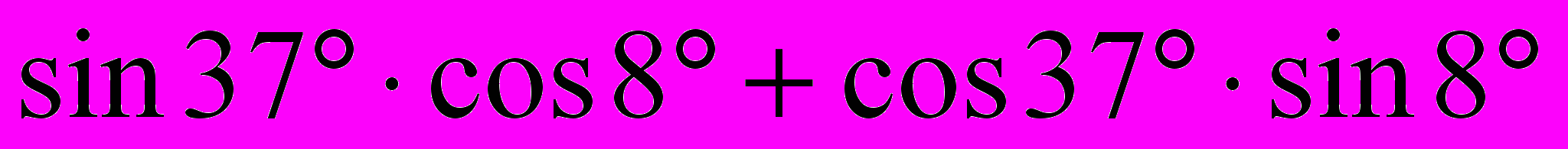 2. a)
2. a) 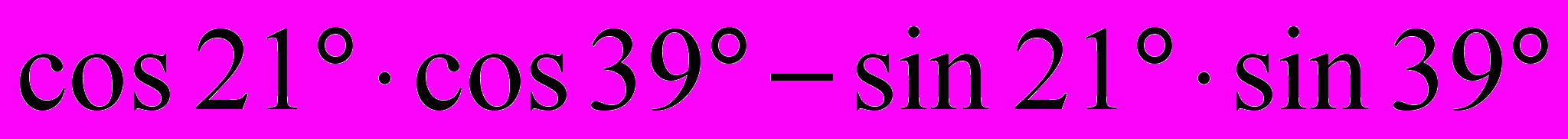
b)
 b)
b) 
c)
 c)
c) 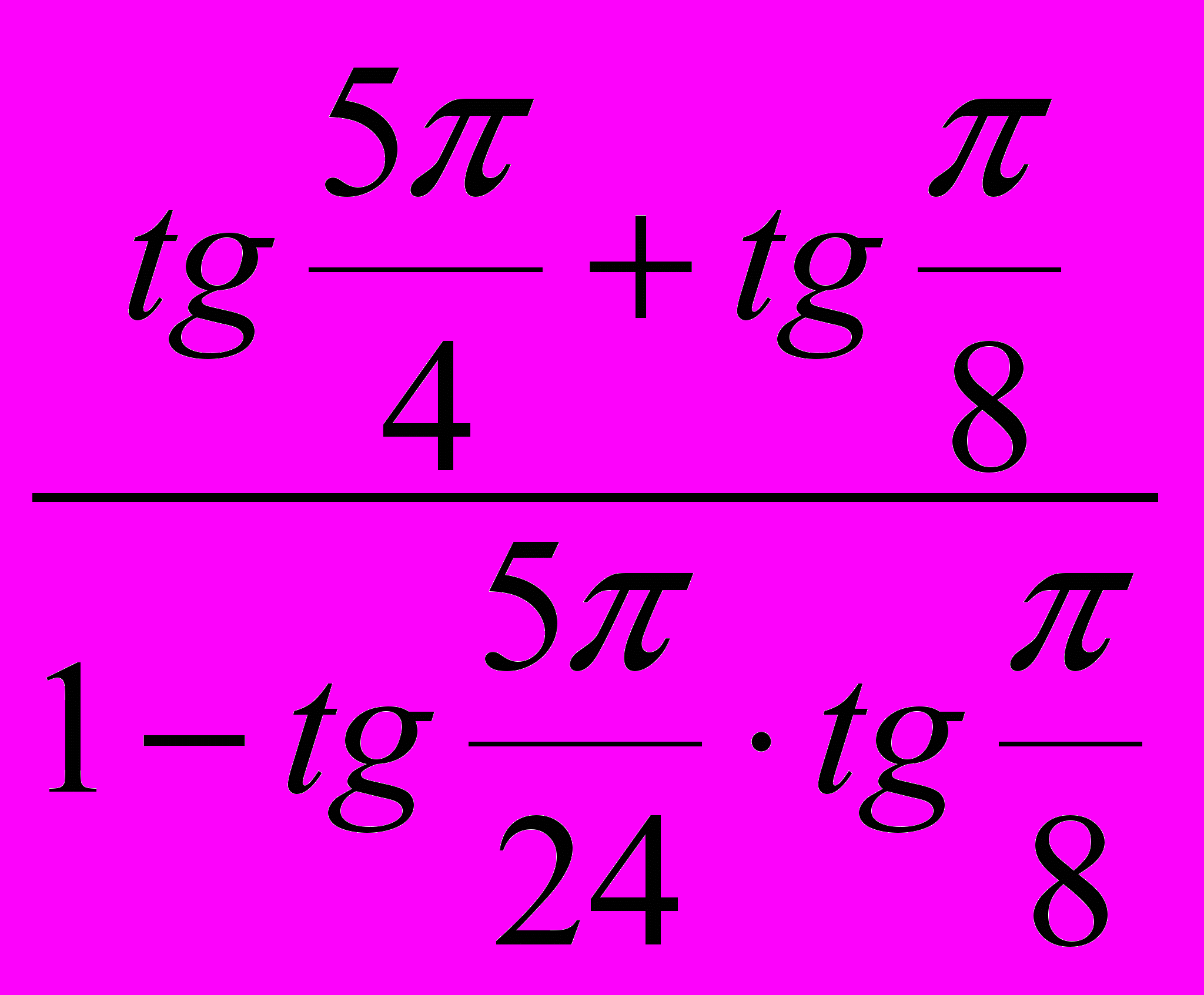
3. Упростить: 3. Упростить:
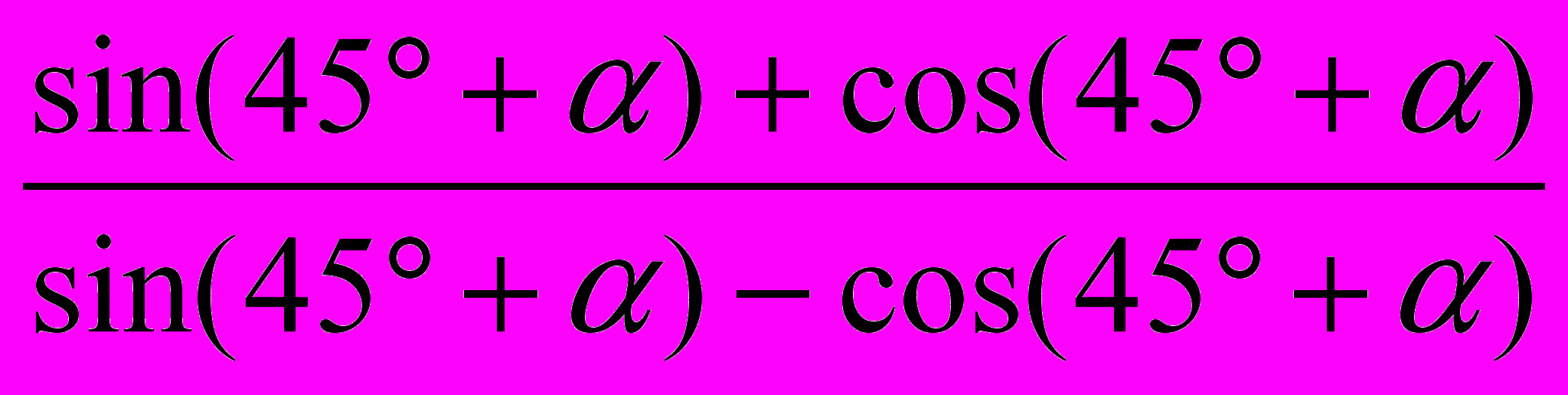
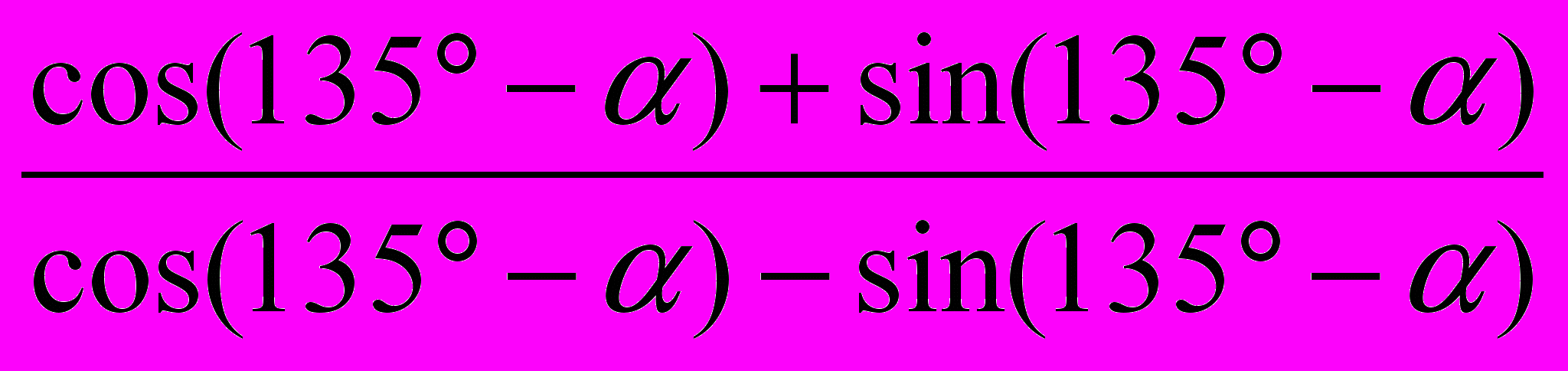
4. Доказать тождество: 4. Доказать тождество:

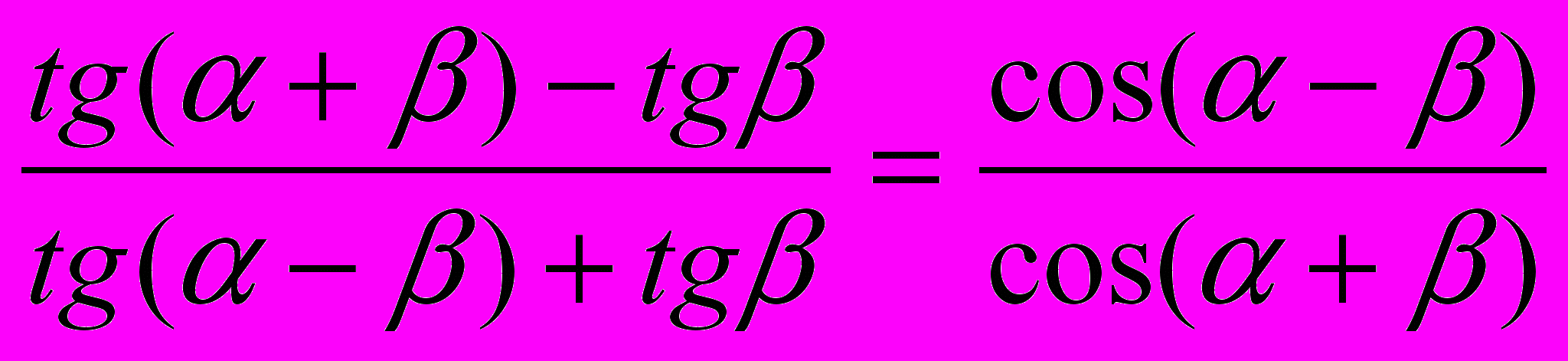
Ответы к заданиям.
| | К-1 | K-2 |
| 1. |  |  |
| 2.a) | 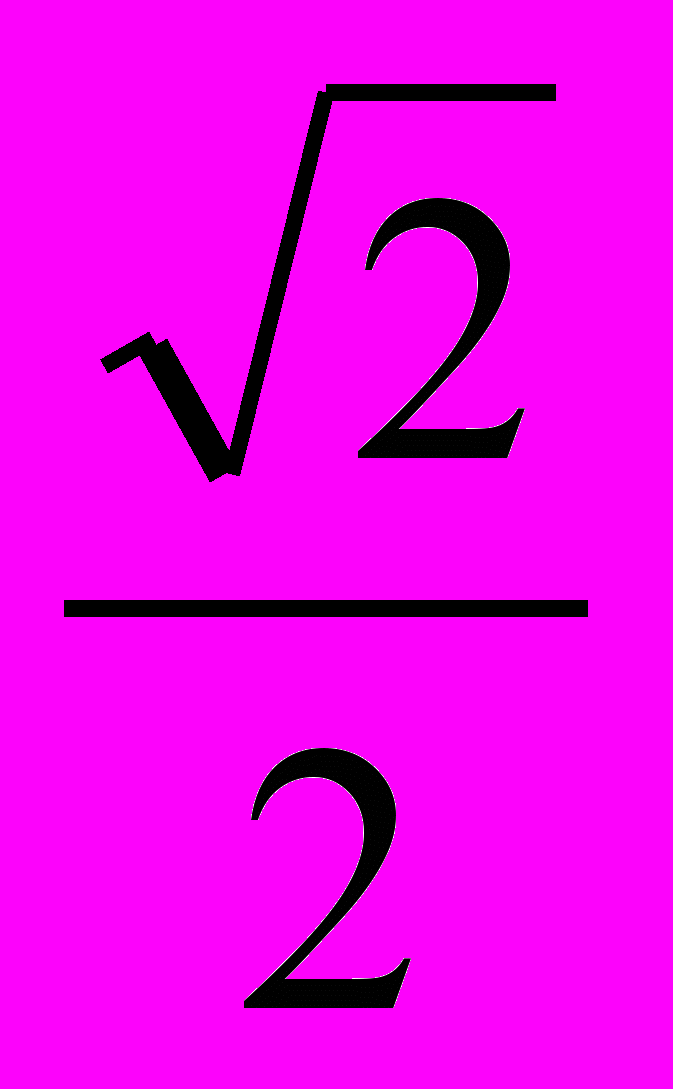 | 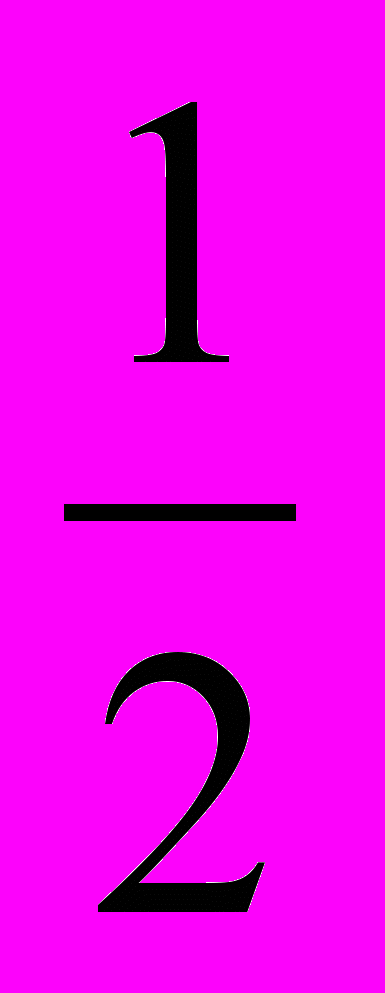 |
| b) | 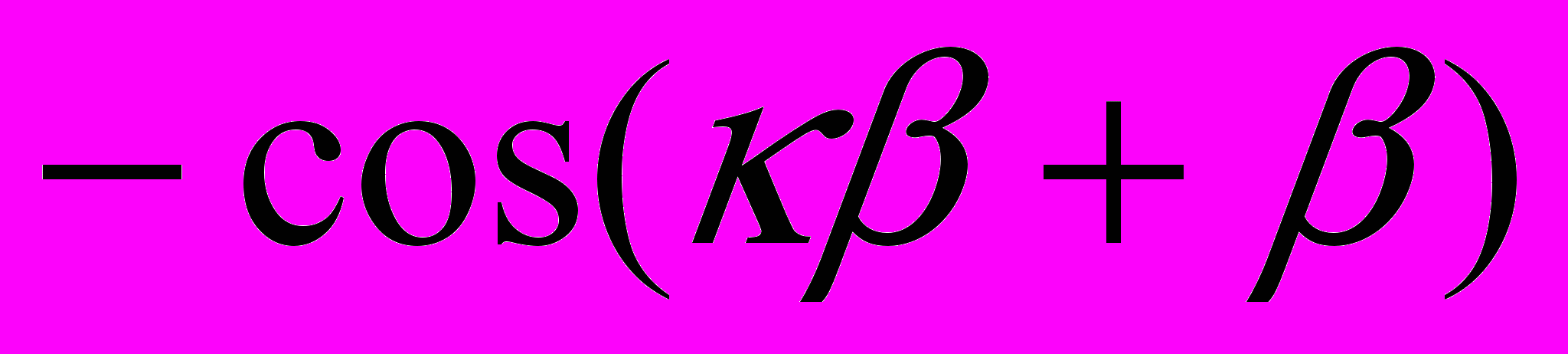 | 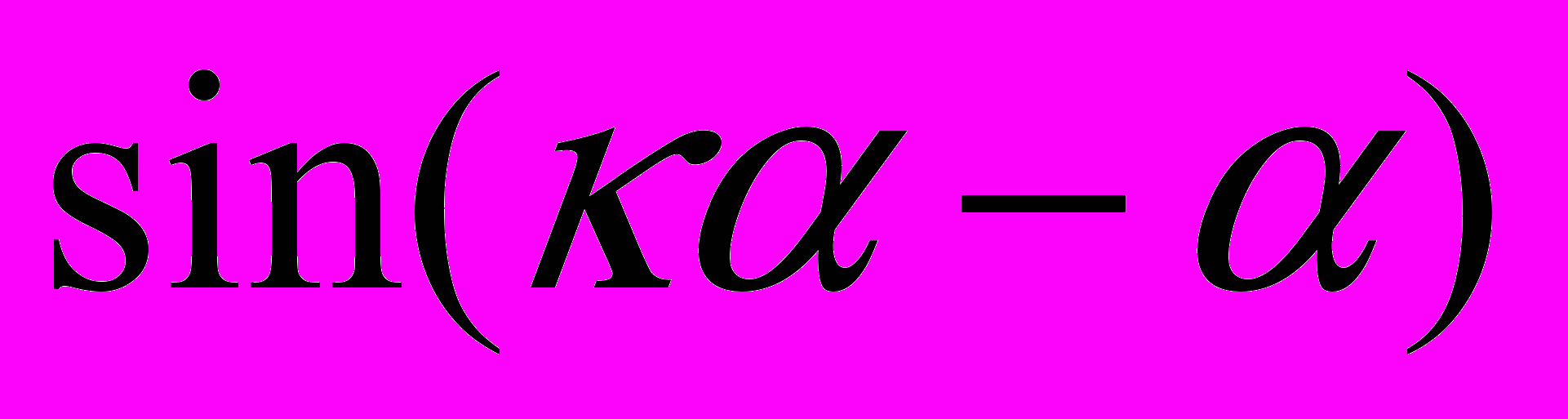 |
| c) | 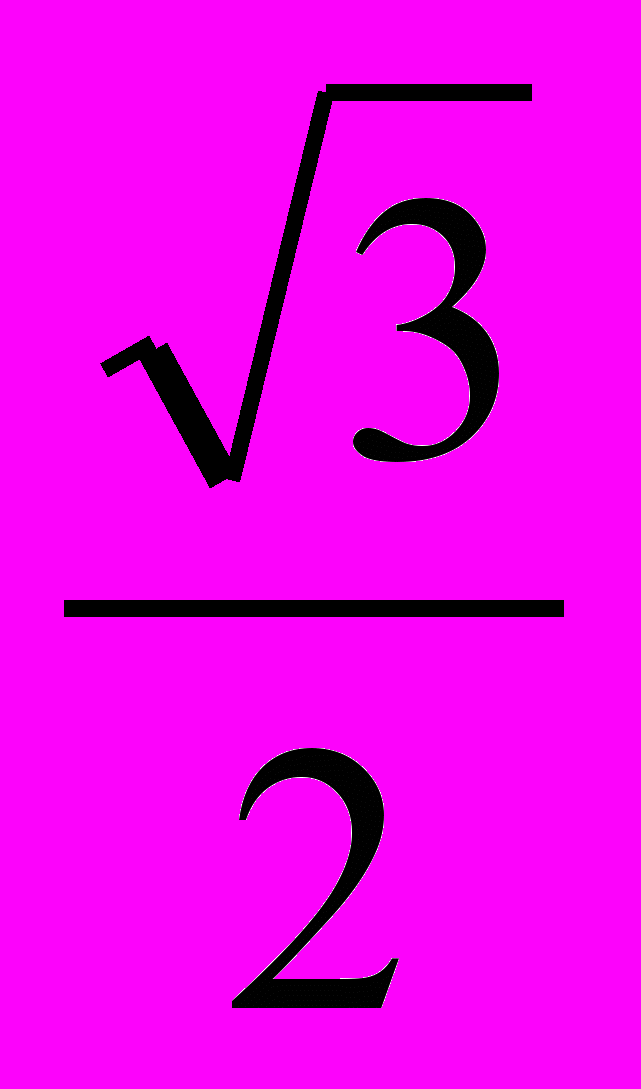 | 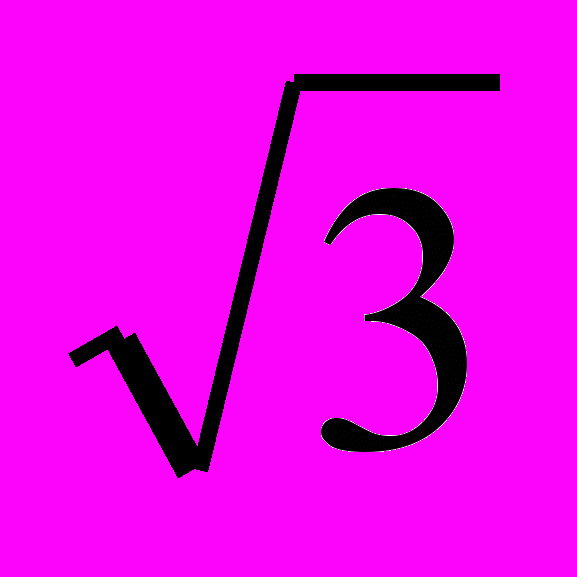 |
| 3. |  | 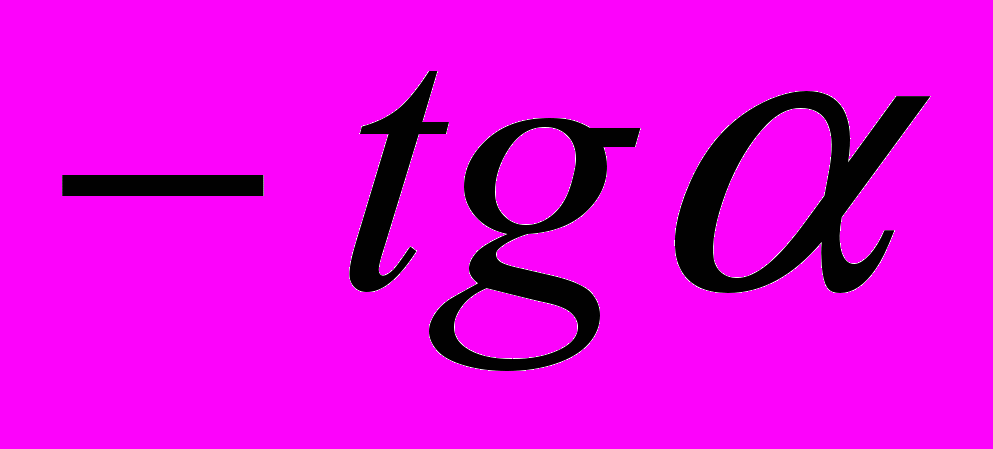 |
На этапе проведения тематического контроля по данной теме целесообразно провести контрольную работу.
Как и в проверочную, в контрольную работу входят в основном задания реконструктивного характера. Но содержание заданий становиться богаче, появляются упражнения, предусматривающие проверку нескольких навыков. Тем не менее, задания в контрольных работах не сложнее тех, которые были рассмотрены учащимися на уроках и дома.
Включение в контрольную работу (в качестве последнего) задания повышенной трудности, требующего от ученика сообразительности, приучает учащихся к творческому подходу, развивает умение применять знания в нестандартной ситуации, вызывает интерес к предмету, дает возможность проявить ученику математические способности, а учителю получить информацию о возможностях его учеников.
Контрольная работа по теме «Элементы тригонометрии».
Цель: проверка умений учащихся применять определение тригонометрических функций, верно выбирать нужную формулу для конкретного преобразования.
В соответствии с поставленной целью задания могут быть следующие.
- Вычислить:
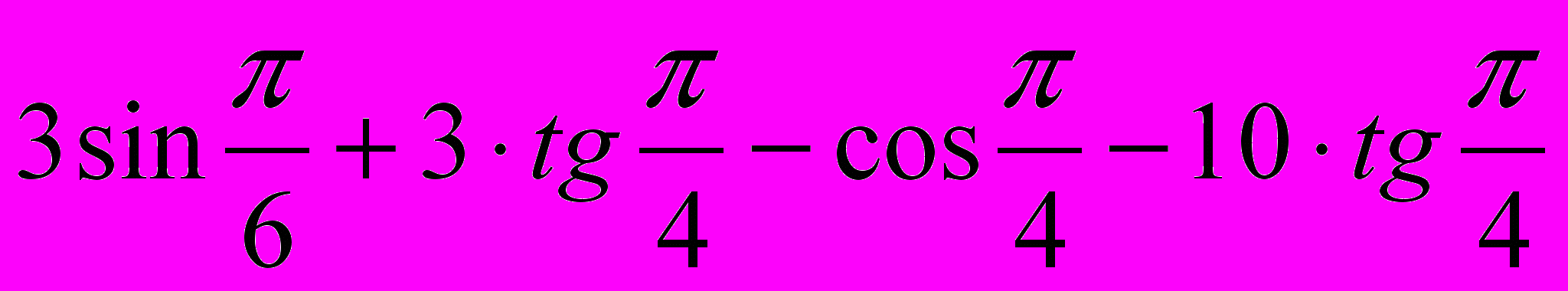
- Определить знак выражения:
a)
 ; b)
; b) 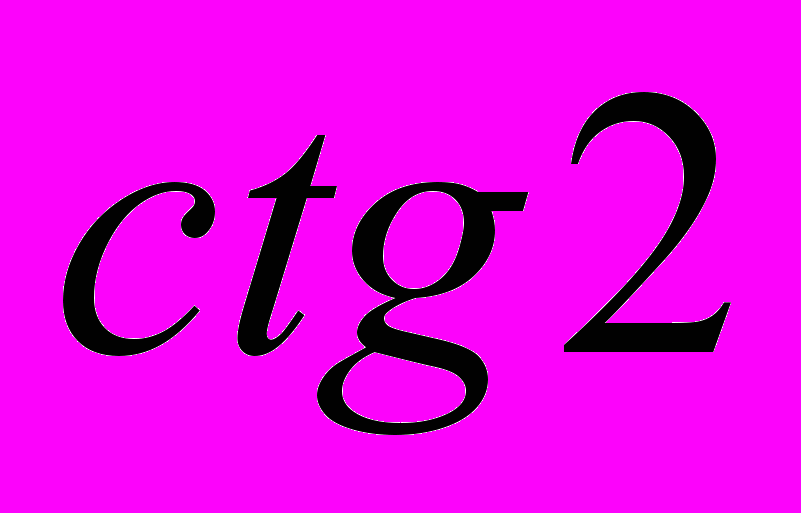
- Изобразить на единичной окружности точки, соответствующие углу , если:
a)
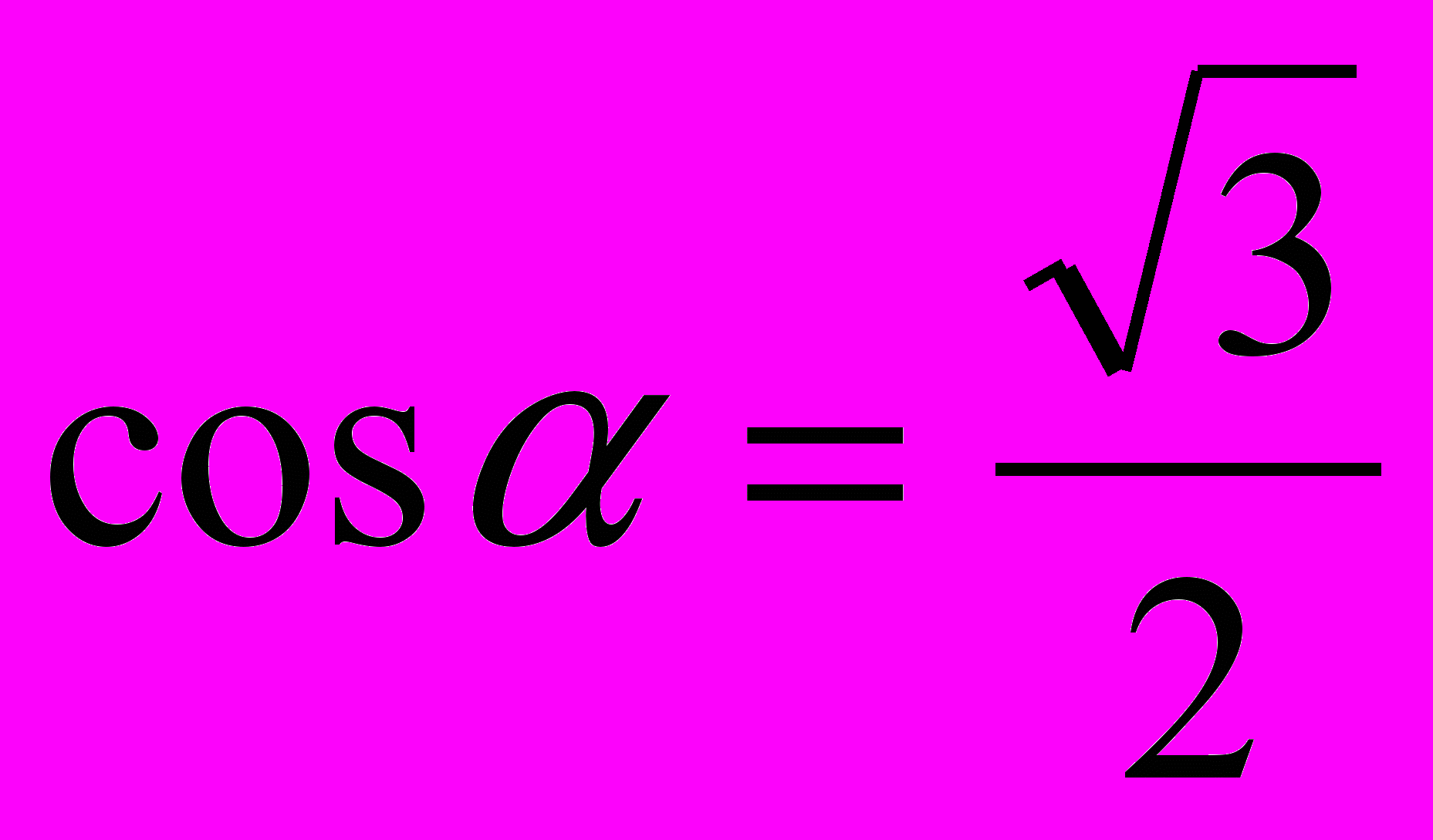
b)
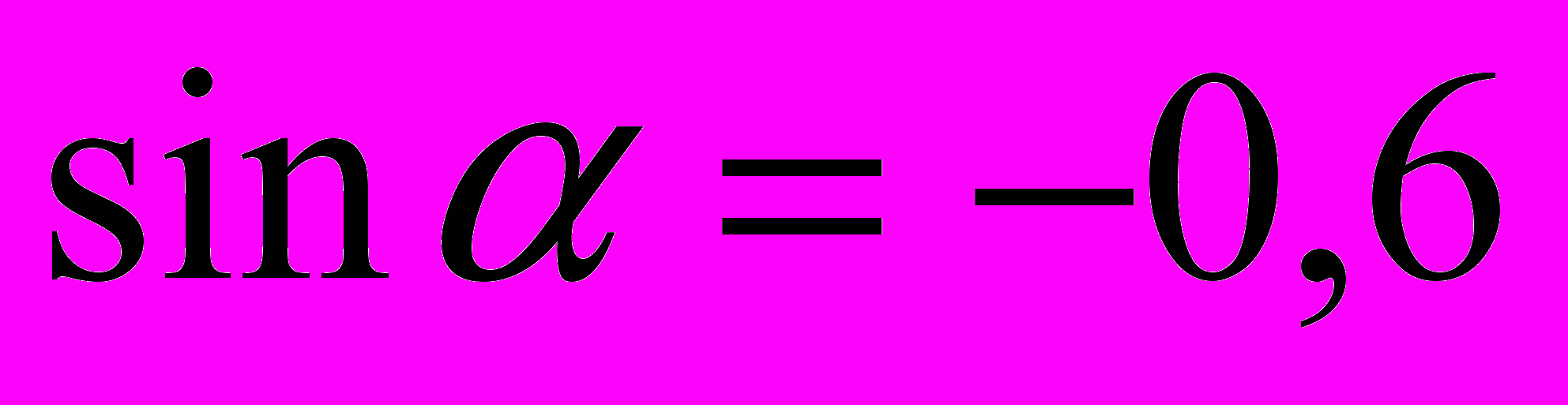
- Избавиться от тригонометрической функции под знаком квадратного корня:
