Методические рекомендации Екатеринбург 2009 удк ббк о

Вид материала

Методические рекомендации

Содержание Основные задачи педагогической практики Содержание деятельности студентов 6. Рекомендации к выполнению задания по ТМОМ 6.2. Пояснительная записка 6.3. Логико-математический анализ изучаемой темы 6.4. Анализ задачного материала

Подобный материал:

• Методические рекомендации Екатеринбург 2006 удк 025. 32 (075. 5) Ббк ч 736., 523.58kb.
• Методические рекомендации Иркутск 2005 ббк удк, 1679.51kb.
• Методические рекомендации г. Пермь 2009 удк 373. 5 Ббк 74. 24(2) Н83 Издание подготовлено, 2317.64kb.
• Методические рекомендации Томск 2009 ббк 73. 3(0)я73 Печатается по решению, 928.69kb.
• Методические рекомендации Ярославль 2005 удк 338. 24; 338. 26; 338. 27 Печатается, 579.59kb.
• Методические рекомендации уфа 2010 удк 636 ббк 45., 880.28kb.
• Методические рекомендации соискателям ученых степеней Оренбург-2005 удк 01(076., 493.32kb.
• Материалы международной студенческой научной конференции 21 апреля 2009 г г. Екатеринбург,, 2547.76kb.
• Методические рекомендации Гродно 2007 удк 37. 018 Ббк 373., 358.38kb.
• Методические рекомендации Минск, 2007 удк ббк, 357.83kb.

5. Программа
педагогической практики студентов 5 курса математического
факультета (направление «Физико-математическое образование», магистерская программа «Математическое образование»)

Цель педагогической практики: формирование у студентов навыков педагога-исследователя, владеющего современным инструментарием науки для поиска и интерпретации информационного материала с целью его использования в педагогической деятельности.

Основные задачи педагогической практики:

1. Продолжить формирование и развитие профессиональных умений и совершенствования навыков профессионально-значимых качеств личности педагога.
   
2. Совершенствовать исследовательские навыки, потребность в самообразовании, развивать умение интерпретировать информационный материал с целью его использования в педагогической деятельности.
   
3. Продолжить формирование у студентов умений применять современные компьютерные технологии в процессе обучения математике, использовать информационные и компьютерные технологии в реализации системы контроля, оценки и мониторинга учебных достижений учащихся.
   

Продолжить приобщение студентов к практической педагогической деятельности, путем вовлечения их в основные компоненты педагогической деятельности: коммуникативный, организаторский, конструктивный, диагностико-корректирующий.

Продолжительность педпрактики 7 недель.

Содержание деятельности студентов

Первые две недели практики

1. Адаптация к условиям образовательного учреждения, знакомство с педагогическим коллективом, изучение конкретных условий организации учебного процесса.
   
2. Знакомство с обучаемыми, проведение их целенаправленного изучения с целью составления психолого-педагогической характеристики и проведения психолого-педагогического анализа познавательной деятельности.
   
3. Посещение всех занятий в закрепленной группе, проведение их частичного анализа.
   
4. Изучение программы, учебников, пособий для преподавателей и студентов, дидактических материалов, методической литературы по текущим темам.
   
5. Разработка плана работы на период практики, графика проведения занятий, определение темы открытых занятий.
   
6. Участие в методических семинарах.
   
7. Проведение пробных занятий.
   
8. Составление плана работы по теме исследования, адаптация теоретического материала к конкретным условиям образовательной среды.
   

Вторая – шестая неделя практики

1. Проведение методических семинаров для студентов 4 курса.
   
2. Разработка и проведение зачетных занятий (не менее 5-ти), которые должны включать в себя урок с использованием проблемного метода обучения.
   
3. Посещение и анализ совместно с групповым руководителем уроков других студентов.
   
4. Проведение зачетного анализа урока одного из студентов.
   
5. Посещение и анализ открытых уроков и зачетных мероприятий других студентов.
   
6. Выполнение индивидуальных заданий по теме исследования.
   
7. Продолжение работы по теме исследования.
   

Седьмая неделя практики

1. Подведение итогов педпрактики в школе.
   
2. Подготовка индивидуальных отчетов.
   
3. Проведение заключительной конференции.
   

Отчетность студента

1. Отчет по работе помощника группового методиста.
   
2. Отчет о выполнении индивидуального задания по теме исследования, в котором отражено следующее:
   

• тема исследования;
  
• цель и задачи исследования;
  
• объект, предмет и гипотеза исследования;
  
• теоретические проблемы исследования, включающие анализ ее основных аспектов;
  
• поисково-констатирующий этап эксперимента; частичная реализация применение идей исследования на практике;
  
• обзор литературы.
  

3. Конспект открытого урока с:
   

• психолого-педагогическим обоснованием поставленной цели урока, отбора математического содержания урока, выбора форм, методов, приемов и средств обучения;
  
• анализом реализации поставленных целей, анализом деятельности учащихся на уроках;
  
• психолого-педагогическим анализом познавательной деятельности учащихся.
  

Итоговая отметка выставляется групповым руководителем в соответствии с отметками:

• за работу студента в качестве помощника группового методиста;
  
• за открытое занятие;
  
• за работу в рамках исследовательской деятельности.
  

6. Рекомендации к выполнению задания по ТМОМ

Логико-дидактический анализ темы

Одним из важных профессиональных умений учителя является грамотное проведение логико-дидактического анализа темы школьного курса математики.

Логико-дидактический анализ темы должен включать в себя следующие компоненты:

1. Психолого-педагогическая характеристика обучаемых.
   
2. Пояснительная записка к данной теме.
   
3. Логико-математический анализ темы.
   
4. Анализ задачного материала с точки зрения основных дидактических функций.
   
5. Внутрипредметные связи темы.
   
6. Межпредметные связи темы.
   
7. Исторический материал.
   
8. Контроль успеваемости учащихся в процессе изучения темы.
   
9. Тематическое планирование.
   

6.1. Составление психолого-педагогической характеристики обучаемых

Для того чтобы провести анализ психологических особенностей учащихся определенной возрастной группы необходимо:

1.1. На основе анализа материала, представленного в учебных пособиях по педагогике и психологии[10,15,16] выделить психолого-педагогические особенности учащихся соответствующего возраста и составить развернутую психолого-педагогическую характеристику учащихся данного класса в соответствии с указанными компонентами:

• характер межличностных отношений в данном коллективе;
  
• мотивация учебной деятельности учащихся;
  
• преобладающий вид внимания;
  
• особенности памяти;
  
• доминирующие виды мышления;
  
• характеристика обучаемости субъектов учебной деятельности;
  

Пример психолого-педагогической характеристикиучащихся 8 «А» класса

В классе обучается 30 человек, из них 15 мальчиков и 15 девочек. Большинство учащихся данного класса отличает повышенная познавательная и творческая активность, они стремятся узнать что-то новое, чему-либо научиться. Группа этих учащихся выходит за пределы школьной программы в развитии своих умений и навыков, т.е. посещает различные кружки, секции, активно участвует в проектной деятельности. На основе таких интересов в классе существуют неформальные группы друзей. На первом месте во взаимоотношениях учащихся стоят товарищеские отношения, которые строятся на таких качествах, как уважение, равенство, верность, готовность прийти на помощь. Особенно осуждаются ребятами данного класса нарушение слова, измена товарищу, стремление командовать, жадность. Такое поведение отвергается и вызывает ответные реакции к нарушителю. Ему могут объявить бойкот, отказать в участии в интересных делах. В классе есть лидеры – это 2 мальчика и 3 девочки. Ребята дорожат личной дружбой с этими учащимися, для некоторых они являются образцом для подражания в плане учебы и личностных качеств. Дети в данном классе заметно отличаются друг от друга по интересу к учению, уровню интеллектуального развития и кругозору, по объему и прочности знаний, уровню личностного развития. У учащихся избирательный характер отношения к школьным предметам. Например, практически весь класс любит историю и литературу, та как их преподают любимые учителя. Примерно 18 учащихся серьезно интересуются математикой и стремятся получить прочные знания по предмету. Мотивация учебной деятельности учащихся в данном классе различная, часть учащихся, желает расширить свои знания, стремится к формированию нужных умений и навыков, позволяющих заниматься интересной работой, самостоятельным творческим трудом. Для некоторых, примерно 10 человек мотивом к учению является только получение хороших отметок. У большинства учащихся данного класса хорошо развито произвольное внимание, т. е. они могут сознательно привлекать и удерживать во внимании на какой либо объекте или предмет деятельности в течение длительного времени, а так же достаточно быстро могут переключаться с одного вида деятельности на другой, если это необходимо. Примерно 7 учеников имеют неустойчивое внимание, это связано с отсутствием интереса к предмету, которое способствует к отвлечению от него. Примерно 20 учеников из класса обладают хорошей слуховой памятью, они быстро запоминают смысл рассказа или читаемого текста, логику рассуждений или доказательства. Следует отметить, что у основной массы учащихся преобладает долговременная память и лишь примерно у 8 учащихся преобладает кратковременная память, которая связана с их актуальными интересами. В мыслительных действиях учащихся 8 «А» класса имеются элементы всех видов мышления, но у большинства учащихся хорошо развито теоретическое понятийное мышление, так как при решении практических задач ребята умеют пользоваться понятиями, формулами, выполняют действия в уме, хорошо используют такие мыслительные операции, как анализ, синтез, обобщение. Примерно 20 учеников данного класса обладает хорошо развитым наглядно-образным и наглядно действенным мышлением, эти учащиеся хорошо строят и читают чертежи, схемы, проводят мысленные и практические преобразования. Следует отметить, что основная часть учащихся данного класса имеют достаточно высокие показатели обучаемости. Двадцать человек в классе учится без троек (11 Девочек и 9 мальчиков) у 18 из них высокий темп продвижения в освоении знаний и формировании умений по всем предметам, лишь две девочки испытывают иногда трудности в процессе изучения математики, но стараются их преодолевать самостоятельно. Неуспевающих в классе нет, 6 учеников имеют тройки по двум – трем предметам. Большинство учеников осознанно относятся к учебе, отличаются высокой работоспособностью, быстро переключаются на новые способы и приемы учебной деятельности.


6.2. Пояснительная записка

Пояснительная записка к теме включает следующие компоненты:

• основные понятия и определения данной темы;
  
• цели изучаемой темы;
  
• знания и умения, которые должны быть сформированы у учащихся в результате изучения данной темы.
  

Пример пояснительной записки к теме «Квадратные уравнения»

Тема «Квадратные уравнения» является продолжением изучения линии уравнений в школьном курсе математики. До этого учащиеся познакомились с линейными уравнениями и их системами, у учащихся отработаны навыки решения линейных уравнений.

Основные понятия и определения данной темы:

• квадратное уравнение;
  
• неполное квадратное уравнение;
  
• приведенное квадратное уравнение;
  
• дискриминант квадратного уравнения;
  
• биквадратное уравнение.
  

К решению квадратных уравнений учащихся следует готовить, начиная уже с 5-го класса.

1. При изучении квадрата числа, натуральной степени числа учащиеся выполняли такие задания: «найти значение выражения D= 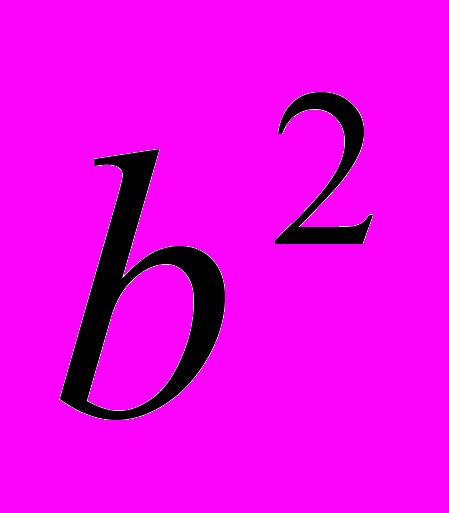— 4ас, если а = 3, b = 7, с = 2». При изучении десятичных дробей, обыкновенных дробей, отрицательных чисел значения а, b, с меняются.

2. Знание квадратов от 1 до 20 нужно проверять на протяжении всех лет обучения математике.

3. К работе по схеме учащиеся готовятся, начиная с устного счета по цепочке, с указанием порядка действий с помощью стрелочек, по элементарным программам при работе с микрокалькулятором. При прохождении многих тем учащиеся учатся выполнять те или другие преобразования по алгоритму.

Цель изучаемой темы: овладение учащимися приемами решения квадратных уравнений как математического аппарата решения разнообразных задач.

Знания и умения, которые должны быть сформированы у учащихся в результате изучения данной темы:

Согласно «Государственному образовательному стандарту образования в период детства, основного общего и среднего (полного) общего образования Свердловской области» от ОЗ.М.1999 № 897-ПП учащиеся должны

Знать:

• определения видов квадратных уравнений (полное, неполное, приведенное); формулы решения квадратных уравнений;
  
• общие методы и обобщенные приемы решения и проверки квадратных уравнений;
  
• способы записи квадратных уравнений;
  
• общий прием решения текстовых задач методом квадратных уравнений.
  

Уметь:

• решать неполные квадратные уравнения;
  
• решать полные квадратные уравнения стандартного вида по формуле и его случаи;
  
• решать приведенные и не приведенные квадратные уравнения по теореме Виета;
  
• решать системы уравнений 2-й степени способом подстановки и сложения;
  
• решать задачи с помощью составления уравнений 1'-й. и 2-й степени и их систем;
  
• решать дробно-рациональные уравнения;
  
• выбрать нужный, рациональный способ решения квадратного уравнения.
  

6.3. Логико-математический анализ изучаемой темы

Логический анализ темы сводится к установлению логической организации учебного материала в теме, выяснению, какие утверждения доказываются, какие вводятся как иллюстрированные факты, определению уровня логической строгости доказательств, методов используемых для доказательств, выделению новых теоретических утверждений, которые вводятся при решении математических задач.

Математический анализ темы сводится к выяснению основной математической идеи темы, выяснению математических обоснований выполняемых преобразований, исследований, доказательств, осмыслению применяемых в теме математических приемов и методов.

Результатом выполнения логико-математического анализа является определение «ядерного» материала темы, логической строгости его изучения и математических методов и приемов изучения этого материала.

Пример логико-математического анализа темы «Неравенства»

Материал темы организован на дедуктивно-индуктивной основе, так как дано определение понятий «больше», «меньше»; свойства числовых неравенств сформулированы в виде теорем, которые доказаны; сформулированные теоремы равносильности (названные свойствами) не доказываются. Анализ решений линейных неравенств с одной переменной и их систем, позволяют учителю сделать обобщение и сформулировать алгоритмы, таким образом алгоритмы вводятся индуктивно. Структура вводимых определений (решения неравенств, равносильных неравенств, решения системы неравенств) одинакова, следовательно, их изучение осуществляется по одному плану, на уровне теоретического обобщения. Теоремы о свойствах неравенств имеют одну и ту же структуру, что позволяет осуществлять перенос знаний, так как с теоремами такой структуры учащиеся уже работали.

Вводятся понятия строгого и нестрогого неравенств, линейного неравенства, системы неравенств.

«Ядерным» материалом темы являются:

• понятия «больше», «меньше», неравенства, решение неравенства, решение системы неравенств, равносильных неравенств;
  
• свойства числовых неравенств, равносильных неравенств;
  
• операции над числовыми неравенствами;
  
• алгоритмы решения неравенств с одной переменной и решения системы неравенств;
  
• прием доказательства неравенств и прием выяснения возрастания, убывания функции.
  

Изложение материала опирается на алгебраические операции, тождественные преобразования, понятие координатной прямой, законы арифметических действий.

При доказательстве свойства числовых неравенств используют логические правила, определения «больше», «меньше». При изучении темы могут быть выбраны следующие методы: объяснительно-иллюстративный, проблемного изложения (например, решения системы неравенств с одной переменной), а так же частично поисковый.


6.4. Анализ задачного материала

Анализ задачного материала выполняется на основе логико-математического анализа теоретического материала темы.

При анализе математических задач необходимо:

1. Определить, какие задачи способствуют раскрытию, конкретизации, углублению «ядерного» материала, основного, объявленного как обязательного в стандарте общеобразовательной школы.
   
2. Выделить задачи на работу с «опорным» материалом, т.е. базовым, исходным для получения нового знания.
   
3. Выделить задачи на «вспомогательный» материал – дополнительный, иллюстративный, раскрывающий межпредметные связи и практические аспекты.
   
4. Выделить нестандартные, творческие задачи.
   

При отборе задачного материала в каждой группе задач необходимо предусмотреть задачи для организации дифференцированной работы с учащимися