На включение программы повышения квалификации педагогических и руководящих работников муниципальных общеобразовательных учреждений Воронежской области в региональный банк программ гоу впо «Воронежский государственный университет»

м.п.

Содержание заявки

Раздел 1. Общая характеристика учреждения

1. Воронежский государственный университет в последние 4 года проводит повышение квалификации по приказам Федерального агентства по образованию РФ преподавателей учреждений начального и среднего профессионального образования России. В текущем году – это повышение квалификации по приказу Рособразования № 2154 от 25.11.2009 г. педагогических работников федеральных государственных образовательных учреждений среднего профессионального образования и учебно-воспитательных учреждений для детей и подростков по направлениям: «Педагогика и психология», «Воспитательная деятельность», «Управление качеством образования», «Информационно-коммуникационные технологии», «Современные педагогические технологии. Новые технологии в изучении и преподавании русского языка».

2. Воронежский государственный университет, начиная с 1967 г. проводит повышение квалификации по приказам Минобразования, Федерального агентства по образованию РФ преподавателей вузов, техникумов, колледжей России. В текущем году – это повышение квалификации по приказам Рособразования № 2142 от 23.11.2009 г. и № 366 от 07.04.2009 г. по 17 направлениям, среди них: «Современные технологии в образовании», «Проблемы качества обучения», «Информатизация образования», «Языковая подготовка ППС», «Молодежь в социальных и политических процессах современной России», «Социально-политические проблемы современного общества», «Гуманитарные проблемы современности», «Математические методы в высшей школе», «Проблемы подготовки кадров по приоритетным направлениям науки, техники, критическим технологиям, сервиса», «Разработка и реализация инновационных программ в области химии», «Современные проблемы экологии и задачи природопользования», «История и философия науки», «Информационная компетентность в профессиональной деятельности преподавателя вуза» и др.

3. В 2009 г. Воронежский государственный университет занял первое место в Рособразовании по количеству преподавателей вузов России, которые прошли в ВГУ повышение квалификации по приоритетным направлениям при самом высоком уровне предложенных курсов. Только по приказам Федерального агентства по образованию РФ в ВГУ прошли повышение квалификации 778 научно-педагогических работников федеральных государственных образовательных учреждений высшего профессионального образования и педагогических работников государственных образовательных учреждений начального профессионального и среднего профессионального образования из Москвы, Санкт-Петербурга, Екатеринбурга, Новосибирска, Нижнего Новгорода, Томска, Челябинска, Перми, Красноярска, Ижевска, Ростова-на-Дону, Ярославля, Брянска, Белгорода, Вологды, Волгограда, Иваново, Кирова, Уссурийска, Курска, Орла, Липецка, Тамбова, Пензы, Архангельска, Тюмени, Грозного, Калининграда и др.


Информация по заявленному направлению подготовки: курсы повышения квалификации учителей математики ориентированы на подготовку учителя к работе в новых условиях реализации приоритетных направлений развития образования, повышение уровня его математической и методической компетентности, расширение общего кругозора.

В процессе обучения будут раскрыты основные идеи совершенствования среднего математического образования. Слушатели познакомятся с современными педагогическими технологиями (технологии коллективного способа обучения, адаптивная система обучения, технология полного усвоения, технология проблемного обучения и др.) и передовым педагогическим опытом. Усвоят особенности дифференциации (уровневой и профильной) и личностно - ориентированного подхода в обучении. Овладеют азами использования информационных и коммуникационных технологий в учебном процессе. Ознакомятся со спецификой обучения математике в общеобразовательных классах, профильных классах различных направлений (естественно-математического, технологического, социально-экономического, гуманитарного) и специализированных классах. Вниманию учителей также будет предложены вопросы осуществления прикладной направленности, а также межпредметных связей в обучении математике.

Кроме того, слушателям будет оказана помощь в овладении содержанием и методическим обеспечением наиболее сложных тем школьной программы (функции и их свойства; уравнения и неравенства с параметрами, в том числе нестандартные приемы их решения; стохастика: элементы комбинаторики, теории вероятностей, статистики; некоторые вопросы стереометрии и др.). Особое внимание будет уделяться выработке умений применять полученные знания к решению задач.

2. Соответствие разработанной образовательным учреждением программы базовым требованиям к содержанию дополнительных профессиональных программ


Воронежский государственный университет имеет более чем 40-летний опыт организации повышения квалификации, разработки и реализации программ дополнительного профессионального образования. Программы, разработанные Воронежским государственным университетом, успешно проходили все независимые экспертизы, проводимые Федеральным агентством по образованию, и полностью соответствуют базовым требованиям к содержанию дополнительных образовательных программ. Разработанная программа также полностью соответствует требованиям, предъявляемым к содержанию дополнительных образовательных программ.

2.1. Результаты освоения программы повышения квалификации

Результатом освоения программы повышения квалификации является получение новых знаний, умений и навыков в различных направлениях деятельности преподавателя или руководителя, подготовка к работе в изменяющихся условиях при проведении реформирования системы образования России, при расширении использования информационно-коммуникационных технологий, приобретение знаний об особенностях применения новых педагогических и информационных технологий, обучение практической работе с необходимыми средствами, методиками, оборудованием. Кроме того, программа поможет учителям математики разрешить свои профессиональные затруднения, а также сформировать и закрепить компетенции необходимые для преподавания предмета на высоком уровне профессионализма.


2.2. Содержание программы повышения квалификации

Приложение 1

Согласовано	Утверждаю
Руководитель организации Заказчика	Руководитель образовательного
	учреждения

УЧЕБНЫЙ ПЛАН

«Современный подход к преподаванию математики в среднем образовательном учреждении»

Цель: совершенствование подготовки педагогических работников в области учебного предмета «Математика» и методики его преподавания

Категория слушателей: учителя математики СОШ, гимназий, лицеев

Срок обучения: 72 часа Режим занятий: 6 часов в день

№ п/п	Наименование разделов и дисциплин	Всего час, в том числе		Форма контроля
		лекции	практич. занятия
1	Инновационная педагогика и современная педагогическая психология	12	4	Собеседование
2	Современное состояние развития научной дисциплины	4
3	Современная методика преподавания математики	22	14	Тестирование, творческая работа
4	Информационные и телекоммуникационные технологии в преподавании предмета	6	10	Презентация
	Итого	44	28

Приложение 2

Утверждаю

Руководитель образовательного

учреждения

У ЧЕБНО-ТЕМАТИЧЕСКИЙ ПЛАН

«Современный подход к преподаванию математики в среднем образовательном учреждении»

Цель: совершенствование подготовки педагогических работников в области учебного предмета «Математика» и методики его преподавания

Категория слушателей: учителя математики СОШ, гимназий, лицеев

Срок обучения: 72 часа

Форма обучения: очная

Режим занятий: 6 часов в день

№ п/п	Наименование разделов, дисциплин и тем	Всего час., в том числе			Форма контроля
		лекции	Выездные занятия, стажировка, деловые игры и др.	Практические лабораторные семинарские занятия
1	Инновационная педагогика и современная педагогическая психология.	12		4	Входное тестирование
1.1	Современные подходы в образовательном процессе.	2		2
1.2	Дифференциация обучения. Профильное обучение.	2
1.3	Новые образовательные технологии в обучении математике.	4		2
1.4	Условия личностной самореализации педагогов. Психологические проблемы современного педагога.	2
1.5	Профилактика конфликтных и конфликтогенных ситуаций.	2			Собеседование
2	Современное состояние развития научной дисциплины.	4
3	Современная методика преподавания математики.	22		14
3.1	Анализ программ, учебников, методических пособий, нормативно-методического обеспечения.	2
3.2	Нестандартные приемы решения тригонометрических уравнений и неравенств.	2		2
3.3	Методы решения иррациональных уравнений и неравенств.	2		2
3.4	Решение задач, содержащих параметры.	2		2
3.5	Комбинаторика, элементы математической статистики, начала теории вероятностей.	4		2
3.6	Нестандартные методы решения задач по планиметрии.	2		1
3.7	Решение стереометрических задач повышенной сложности. Построение сечений многогранников, вычисление их площадей.	2		1
3.8	Основы математического анализа.	2		2
3.9	Решение олимпиадных задач по математике.	2		2
3.10	Преподавание математики в условиях ЕГЭ.	2			Тестирование, творческая работа
4	Информационные и телекоммуникационные технологии в преподавании предмета.	6		10
4.1	Использование компьютера при обучении математике.	4		4
4.2	Учебные компьютерные презентации.	2		6	Презентация

Приложение 3

Воронежский государственный университет

УЧЕБНАЯ ПРОГРАММА КУРСА

«Современный подход к преподаванию математики в среднем образовательном учреждении»

1. Инновационная педагогика и современная педагогическая психология

Тема 1. Современные подходы в образовательном процессе

Модернизация Российского образования. Концепция профильного обучения, основы разработки элективных курсов. Приоритетный национальный проект «Образование».

Тема 2. Дифференциация обучения. Профильное обучение

Технология дифференцированного обучения, личностно – ориентированный подход в обучении. Основные направления профильного обучения. Особенности работы в профильных и специализированных классах.

Тема 3. Новые образовательные технологии в обучении математике

Необходимость использования современных образовательных технологий. Технология саморазвивающего обучения, осмысленно-концентрированное обучение, коллективный способ обучения. Практическое использование элементов технологий в преподавании математики.

Тема 4. Условия личностной самореализации педагогов. Психологические проблемы современного педагога

Актуализации индивидуального потенциала профессионального развития, приемы выявления и анализ профессиональных затруднений. Анализ психологических проблем современного педагога и пути их разрешения.

Тема 5. Профилактика конфликтных и конфликтогенных ситуаций

Понятие конфликта. Общая характеристика конфликтов. Классификация конфликтов. Объективные, организационно-управленческие, социально-психологические и личностные причины конфликтов. Школа как модель общества. Причины возникновения конфликтов в школе. Конфликты между руководителем и подчиненным. Психологические механизмы возникновения межгрупповых конфликтов. Предупреждение и разрешение конфликтов. Принципы и условия предупреждения конфликтов. Основные способы и приемы разрешения межличностных конфликтов. Урегулирование конфликтов с участием третьей стороны.

2. Современное состояние развития научной дисциплины

Реализация концепции беспрерывного математического образования. Основные направления развития математической науки. Практическая реализация: применение вероятностных методов теории массового обслуживания, решение задач, связанных с оптимизацией очередей, управление запасами, решение некоторых экономических задач. Требования к изучению дисциплины на современном этапе. Связь математики с другими науками. Востребованность специалистов.

3. Современная методика преподавания математики

Тема 1. Анализ программ, учебников, методических пособий, нормативно-методического обеспечения.

Стандарт математического образования, программы различного уровня обучения (общеобразовательные, профильные, углубленные). Федеральный перечень учебников. Альтернативные учебники, рекомендованные Министерством образования и науки РФ. Учебники базового и профильного уровней.

Тема 2. Нестандартные приемы решения тригонометрических уравнений и неравенств.

Классификация тригонометрических уравнений. Решение нестандартных тригонометрических уравнений и неравенств, используя различные методы решения: умножение обеих частей уравнения на одну и ту же тригонометрическую функцию, преобразование тригонометрических выражений, использование свойства пропорции и др. Решение тригонометрических уравнений и неравенств с двумя переменными. Уравнения и неравенства с обратными тригонометрическими функциями.

Тема 3. Методы решения иррациональных уравнений и неравенств.

В теме рассматриваются методы решения иррациональных уравнений и неравенств: возведение в степень, замены, сведение к системе, умножение на сопряженное, оценки, с использованием векторов и др.

Тема 4. Решение задач, содержащих параметры.

Теоретические основы и методы решения уравнений и неравенств с параметрами, которые изучаются в курсе математики средней школы: линейных, квадратных, иррациональных, тригонометрических, показательных и логарифмических. Знакомство с нестандартными методами решения задач с параметрами.

Тема 5. Комбинаторика, элементы математической статистики, начала теории вероятностей.

Понятие выборки элементов, общие правила комбинаторики. Комбинаторные принципы сложения и умножения. Основные формулы и их использование при решении задач о числе размещений, перестановок и сочетаний (без повторений и с повторениями). Задачи, связанные с биноминальной формулой Ньютона. Сложная комбинаторика. Введение понятия случайного события и операций над ними. Различные подходы к определению вероятности, частота события. Операции над вероятностями, формула полной вероятности. Независимые повторные испытания (формула Бернулли). Случайные величины, их распределения и числовые характеристики. Методы статистического анализа. Представление данных

Тема 6. Нестандартные методы решения задач по планиметрии.

Метод дополнительных построений, переход к равновеликим фигурам, применение векторной алгебры, алгебраические и тригонометрические решения планиметрических задач. Разбор многовариантных задач повышенной сложности.

Тема 7. Решение стереометрических задач повышенной сложности. Построение сечений многогранников, вычисление их площадей.

Нестандартные методы решения задач стереометрии (векторный, переход к разверткам, дополнительные построения и др.). Приемы построения сечений, выбор удобного ракурса при выполнении чертежа.

Тема 8. Основы математического анализа

Понятие функции, особенности введения этого понятия в классах различного уровня обучения. Понятие производной, решение задач различного уровня сложности с использованием физического и геометрического смысла производной. Решение нестандартных задач и задач с параметром по данной теме. Понятие криволинейной трапеции и вычисление ее площади.

Тема 9. Решение олимпиадных задач по математике

Система приемов формирования у учащихся нестандартного мышления. Реализация этих приемов при решении олимпиадных задач. Комплекс задач, способствующих воспитанию интереса к математике и развитию мыслительных способностей.

Тема 10. Преподавание математики в условиях ЕГЭ

Анализ структуры тестовых контрольных работ единого государственного экзамена. Оформление решений заданий вида «С». Критерии оценки результатов.

4. Информационные и телекоммуникационные технологии в преподавании предмета

Тема 1. Использование компьютера при обучении математике

Мультимедийные программы, используемые на уроках математики. Возможности интерактивных досок и их роль в повышении эффективности уроков. Интернет и его возможности при обучении математике.

Тема 2. Учебные компьютерные презентации

Создание компьютерных презентаций по темам школьного курса математики.

Методические рекомендации и пособия по изучению курса или дисциплины

1. Евсюк С.Л. Математика. Решение задач повышенной сложности. - Мн: «Мисанта», 2003.

2. Лурье М.В. Геометрия. Техника решения задач. Учебное пособие. - Ростов н/Д.: Феникс;.М.: Издательский отдел УНЦ ДО. 2002.

3. Кожарин А.Ф., Лебедев В.К., Давыдова И.Л. Алгебра и геометрия. Методика и практика преподавания.- Ростов н /Д: «Феникс». 2002

4. Олехник С.Н., Потапов М.К., Пасиченко П.И. Уравнения и неравенства. Нестандартные методы решения. – М.: Дрофа, 2001.

5. Саранцев Г. Методика обучения математике в средней школе. -М.: Просвещение, 2002.

6. Селевко Г.К. Современные образовательные технологии: Учебн. пособие. - М.: Народное образование, 1998.

7. Шарыгин И.Ф. Сборник задач по геометрии. 5000 задач с ответами. -М.: ООО «Издательство Астрель», 2001.

8. Афанасьева Т.П., Немова Н.В. Профильное обучение: педагогическая система и управление. Книга 1, 2. Система профильного обучения старшеклассников. Методическое пособие / Под редакцией Н.В. Немовой. - М.: АПК и ПРО, 2004.

9. Моденов В.П. Задачи с параметрами. Координатно-параметрический метод: учебное пособие / В.П. Моденов. - М.: Издательство «Экзамен», 2006.

10. Шахмейстер А.Х. Задачи с параметрами в ЕГЭ. - СПб.: «ЧеРо-на-Неве», 2004.

11. Тавгень О.И., Тавгень А.И. Математика в задачах. Теория и методы решений. Уравнения, неравенства, системы. АВЕРСЭВ. Минск, 2005.

12. Голубев В.И. «Решение сложных и нестандартных задач по математике» Илекса, Москва, 2007.

13. Готман Э.Г. «Стереометрические задачи и методы их решения». М.:МЦНМО. – 2006.

14. Азаров А.И., Булатов В.И., Федосенко В.С., Шибут А.С. «Решения тригонометрических уравнений» «Тетра Системс». – Минск, 2003г.

15. Калинин С. И., Канин Е.С. и др. Задачи и упражнения по началам математического анализа. М., Московский Лицей, 2002.

16. Колесникова Т.В., Колесников О.Н. Алгебра и начала анализа. Сборник заданий для подготовки к итоговой аттестации. М.: Издательство «Экзамен», 2006.

2.3. Условия реализации программы повышения квалификации

Воронежский государственный университет для организации повышения квалификации имеет учебные аудитории, оснащенные самым современным

оборудованием, в том числе новые лекционные аудитории с компьютерными проекторами и Интернетом, аудитории для практических занятий и компьютерные классы, оснащенные мультимедийными системами, интерактивными досками, Wi-Fi, компьютерными сетями, электронными библиотеками и т.д.

2.4. Использование новых форм и методов организации образовательного процесса в образовательном учреждении в соответствии с базовыми требованиями к содержанию дополнительных профессиональных образовательных программ

В Воронежском государственном университете используются новые формы и методы организации образовательного процесса в соответствии с базовыми требованиями к содержанию дополнительных профессиональных образовательных программ: новые педагогические, информационные и компьютерные технологии, учебно-методические комплексы, технологии дистанционного обучения, методы разработки и ведения электронных учебных курсов, Интернет-технологии, современные информационные сети, мультимедийные средства и др.


3. Контрольные задания

Вопросы к собеседованию:

1. Определение понятия «педагогическая технология».
   
2. Основные особенности образовательных педагогических технологий, их классификация.
   
3. Кратко охарактеризуйте одну из современных педагогических технологий.
   
4. Каковы условия личностной самореализации педагога?
   
5. Охарактеризуйте понятие «профессиональная компетенция педагога».
   
6. В чем проявляется влияние учебной деятельности на эмоциональную сферу учащихся?
   
7. Раскройте смысл понятия «педагогическое взаимодействие»?
   
8. Что является важнейшим условием личностной самореализации?
   
9. Каковы интегральные свойства лидера?
   
10. Понятие самореализации и ее роль в жизни личности.
    
11. Каковы педагогические условия, обеспечивающие формирование готовности педагога к инновационной деятельности?
    
12. Противоречия в реализации инновационной деятельности педагогами.
    
13. Каковы компоненты и критерии готовности педагога к инновационной деятельности?
    
14. Назовите современные подходы к организации процесса формирования готовности к инновациям.
    

Темы творческих проектов и рефератов:

1. Укрупнение дидактических единиц учебной информации (УДЕ) при обучении математике.
   
2. Использование нетрадиционных форм обучения (урок-семинар, урок-конференция, урок-лекция и др.) и её результативность.
   
3. Дифференцированное обучение на уроках математики - как средство развития индивидуальных способностей школьников.
   
4. Пути реализации межпредметных связей в процессе изучения математики.
   
5. Групповая работа - как одна из форм деятельности учащихся на уроке.
   
6. Преемственность в обучении математике.
   
7. Идеи педагогики сотрудничества при обучении математике.
   
8. Развитие пространственных представлений учащихся в процессе изучения курса геометрии.
   
9. Пути формирования логического мышления учащихся.
   
10. Пути формирования приемов мыслительной деятельности учащихся.
    
11. Игровые элементы при обучении математике - как средство привития интереса к предмету.
    
12. Организация индивидуальной работы с учащимися как средство повышения уровня учебных достижений учащихся.
    
13. Формирование навыков самостоятельности в процессе обучения математике.
    
14. Формирование познавательного интереса на уроках математики.
    

22. Руководство процессом самостоятельного усвоения учебного материала на уроках математики.
    
23. Развитие абстрактного мышления в процессе решения алгебраических задач.
    
24. Использование наглядности на уроках математики.
    
25. Методика преподавания статистики на уроках математики.
    
26. Методика преподавания комбинаторики на уроках математики.
    
27. Методика преподавания теории вероятностей на уроках математики.
    
28. Тестовые задания, методика и технология их составления и использования.
    
29. Формирование приемов самоконтроля в процессе изучения математики в старших классах.
    
30. Особенности преподавания отдельных тем, вызывающих затруднения (комбинаторика, теория вероятностей, математическая статистика, простые и сложные проценты и т. д.) в классах физико-математического, экономического, естественного профилей.
    
31. Развитие познавательной активности учащихся в процессе изучения спецкурсов и факультативов по математике.
    
32. Выявление и организация работы с одаренными детьми как средство развития интеллекта и индивидуальных способностей ребенка.
    
33. Использование компьютерных технологий в обучении математике.
    
34. Использование элементов новых образовательных технологий в преподавании математики.
    
35. Реализация принципов развивающего обучения на уроках математики.
    

Примеры контрольно измерительных материалов:

№1. 1) Решить уравнение: .

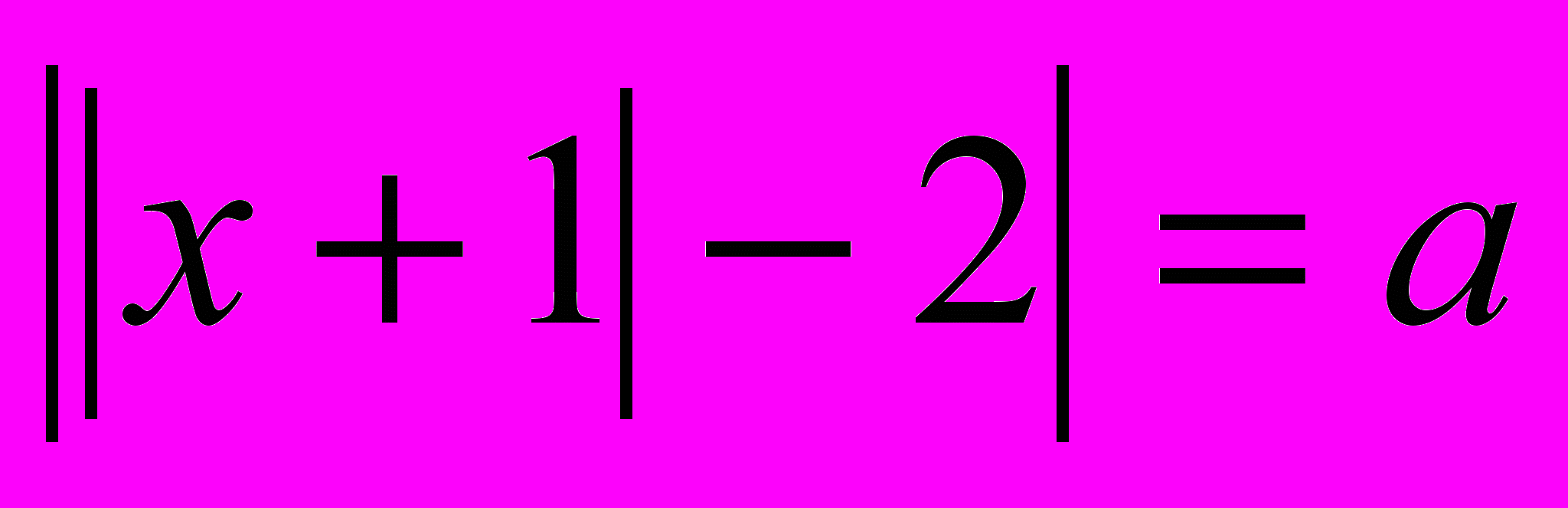2) При каждом значении параметра а решить уравнение .

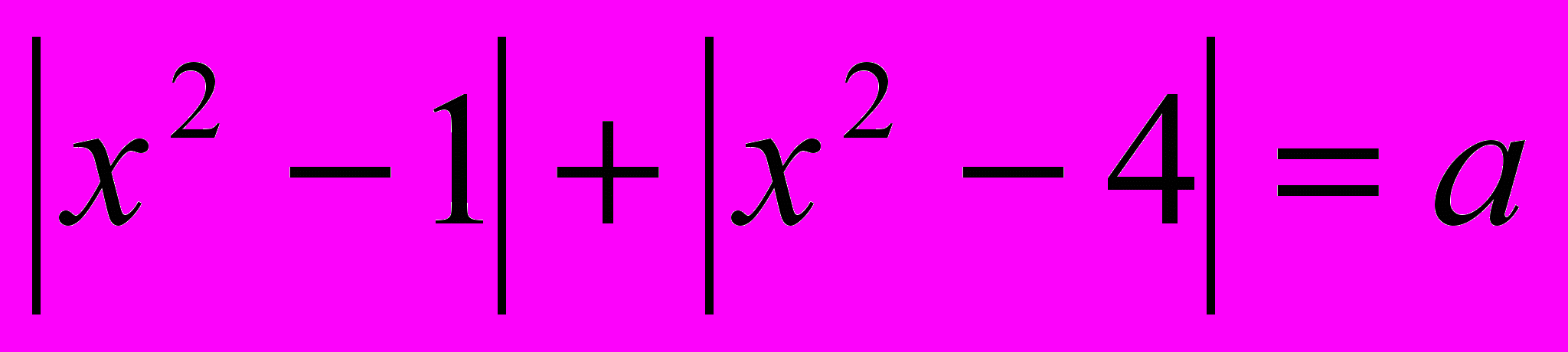3) При каких значениях параметра система 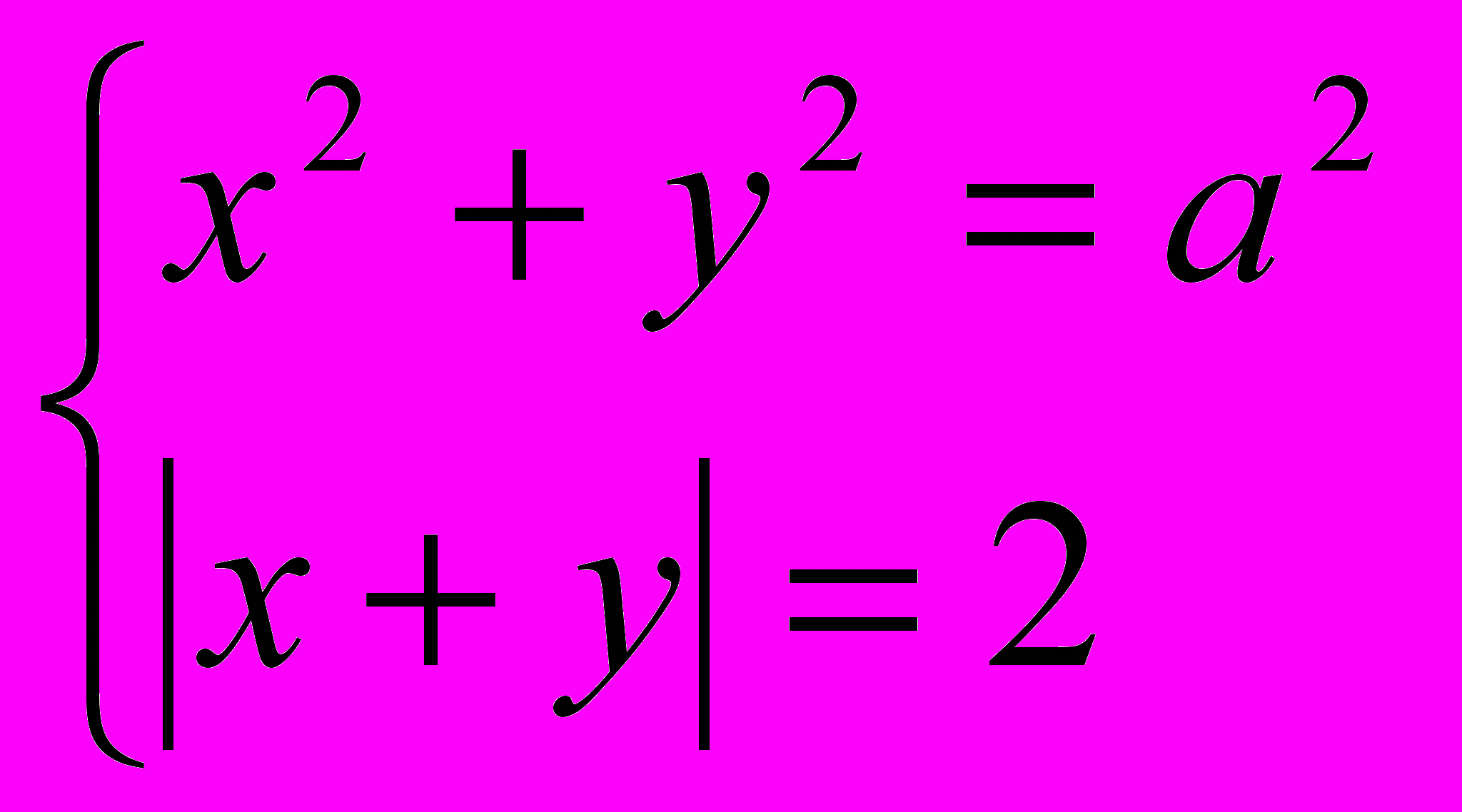имеет ровно 2 решения?

4) При каких значениях а уравнение 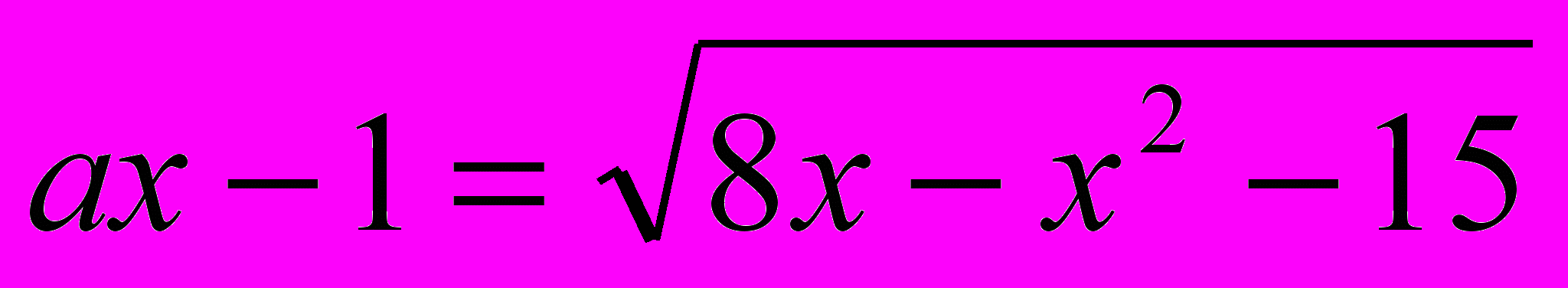имеет единственное решение?

5) Решить неравенство .


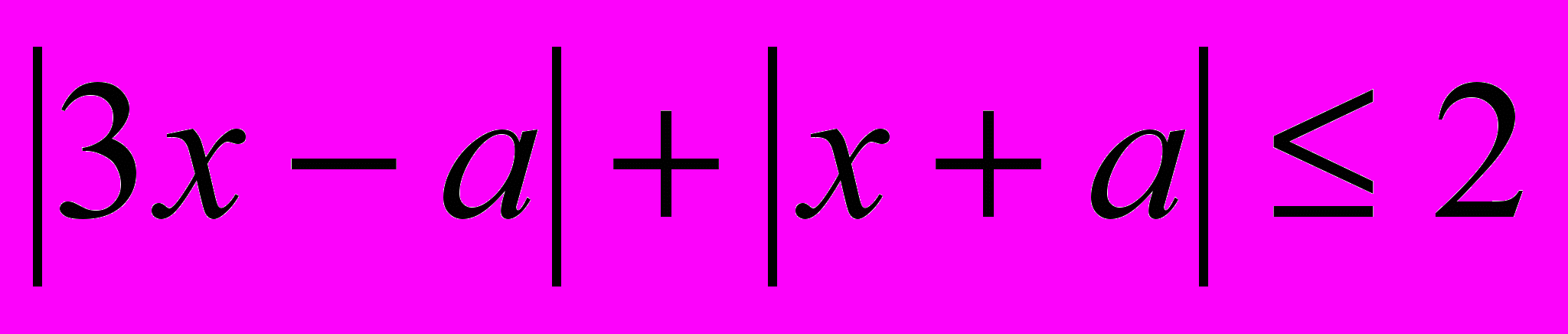№2. 1) Решите уравнение: .

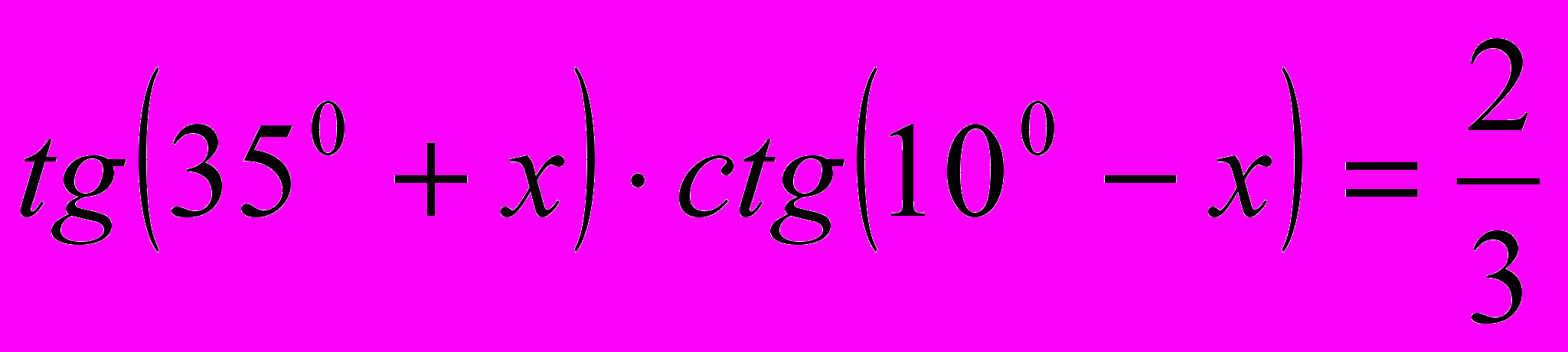2) .

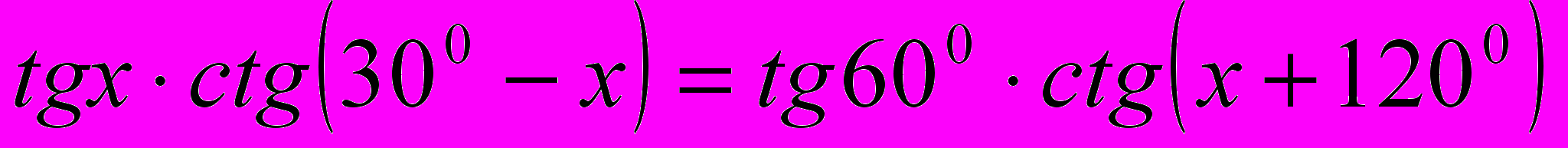3) .

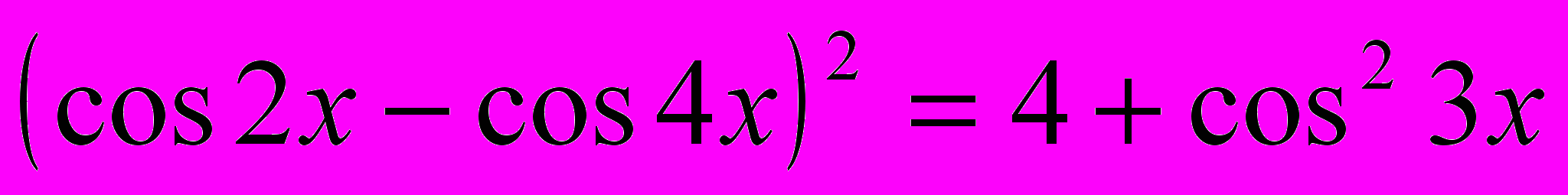4) .

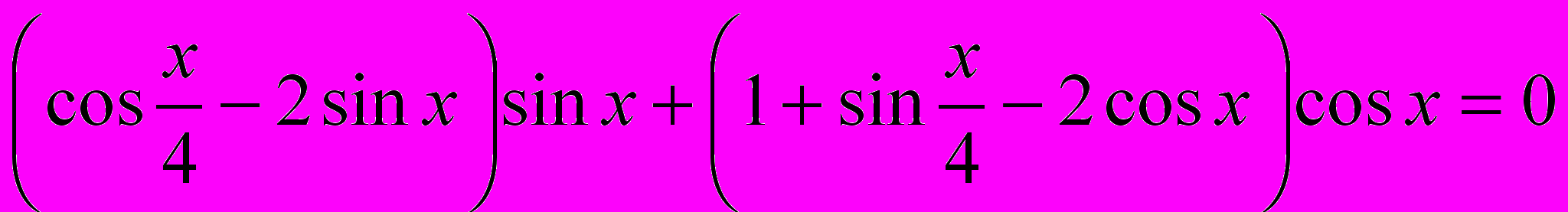5) .


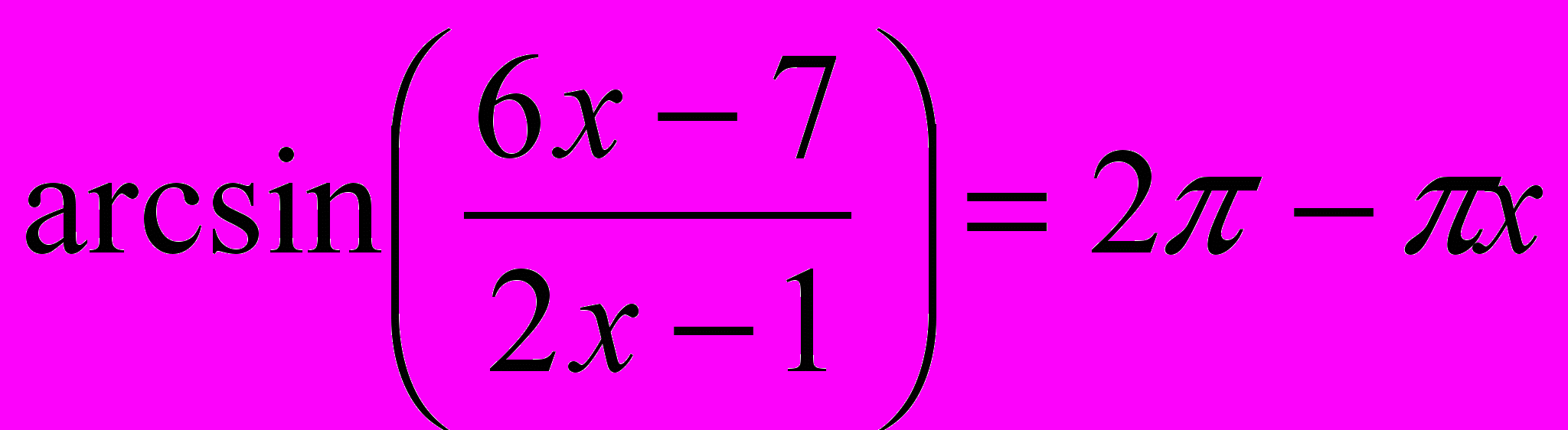№3. 1) Даны две функци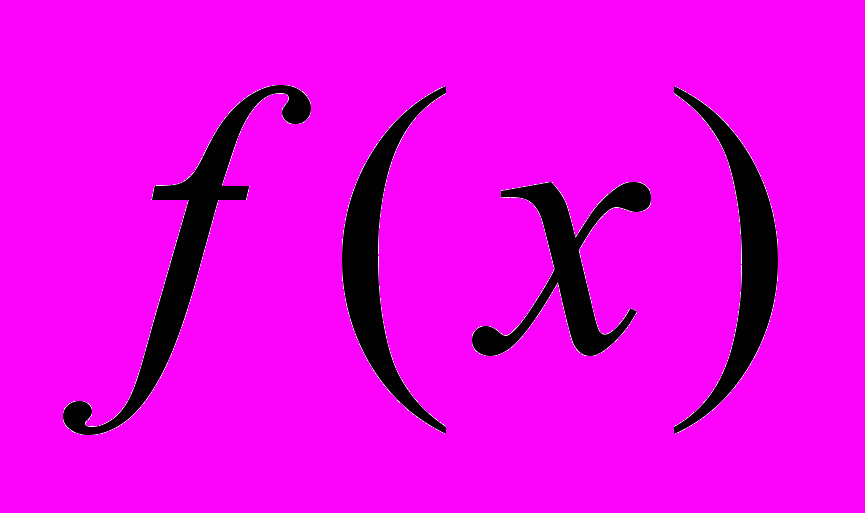и и 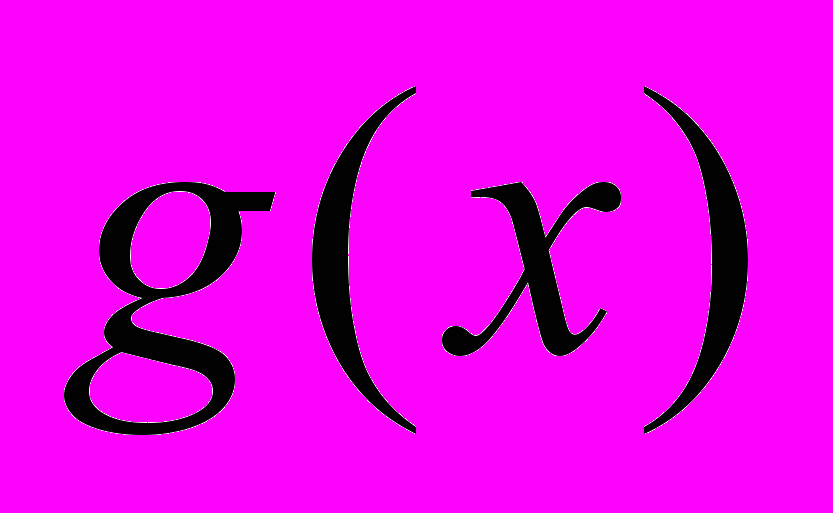. Найдите, при каких 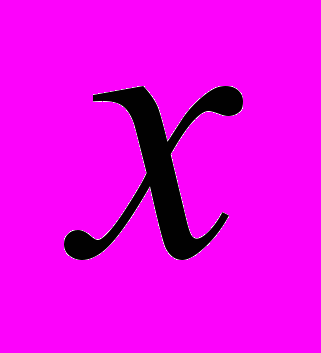имеет место равенство 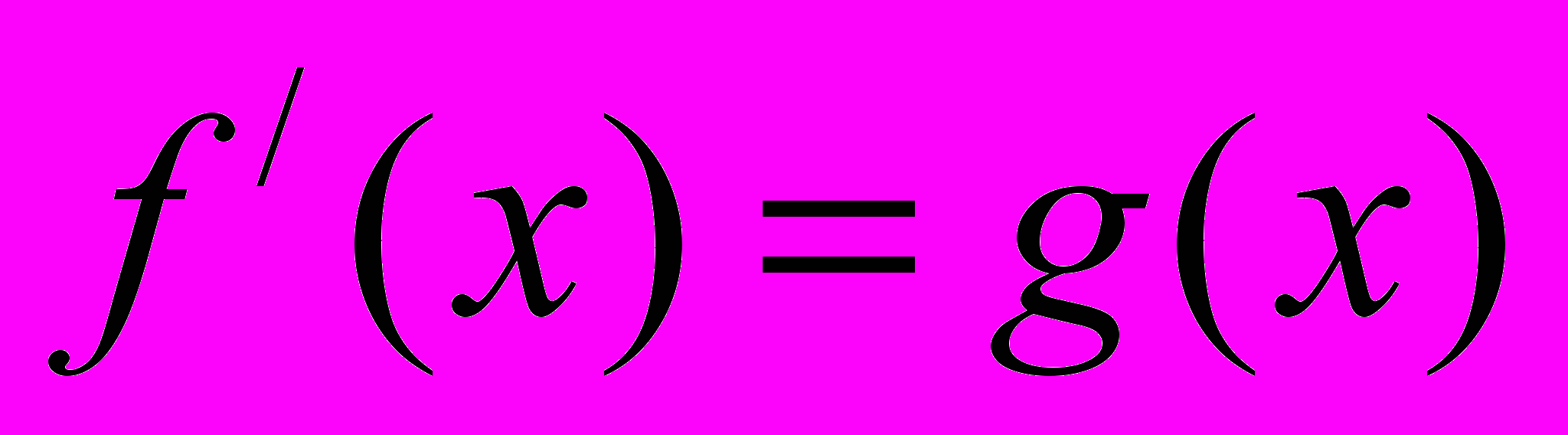, есл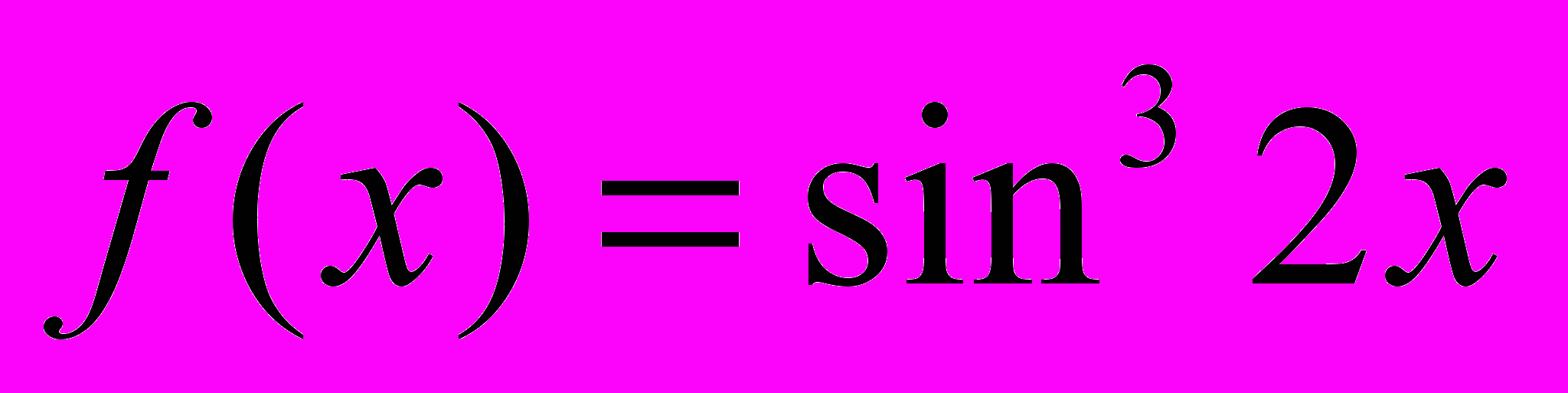и и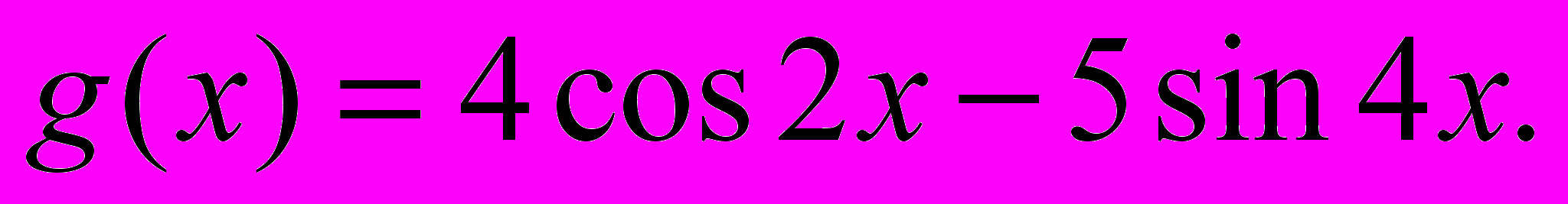

2) При каких значениях и 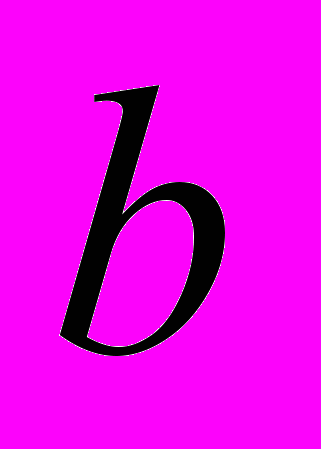все экстремумы функции 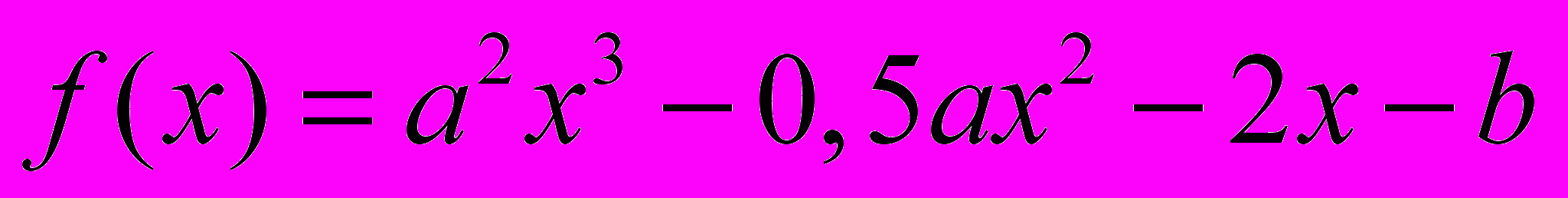положительны и минимум находится в точке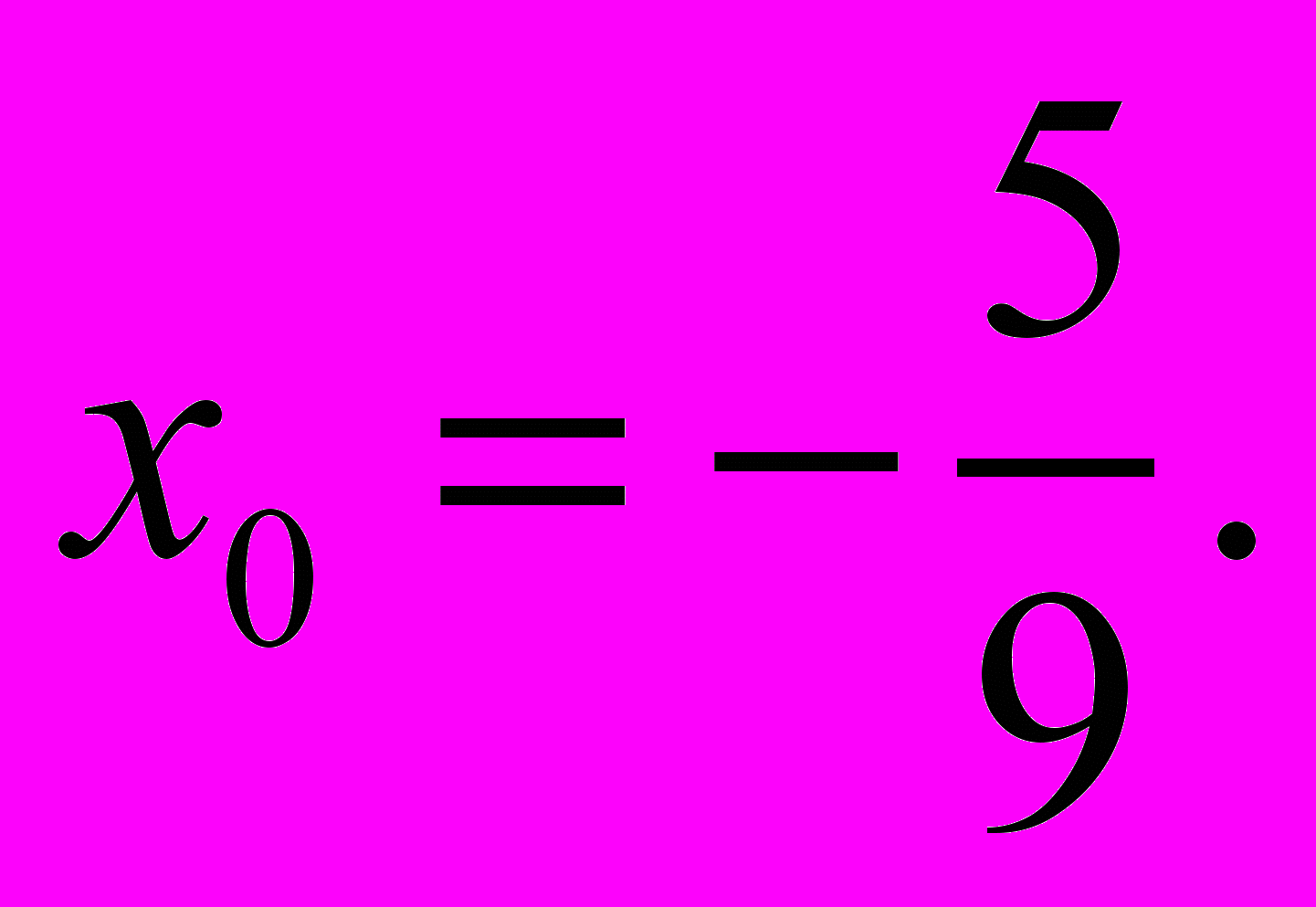

3) Найти наибольшее значение функции 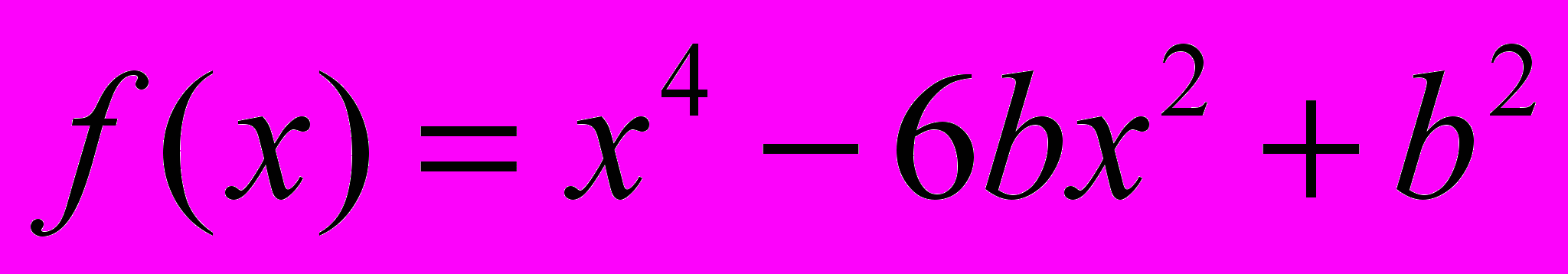на отрезке 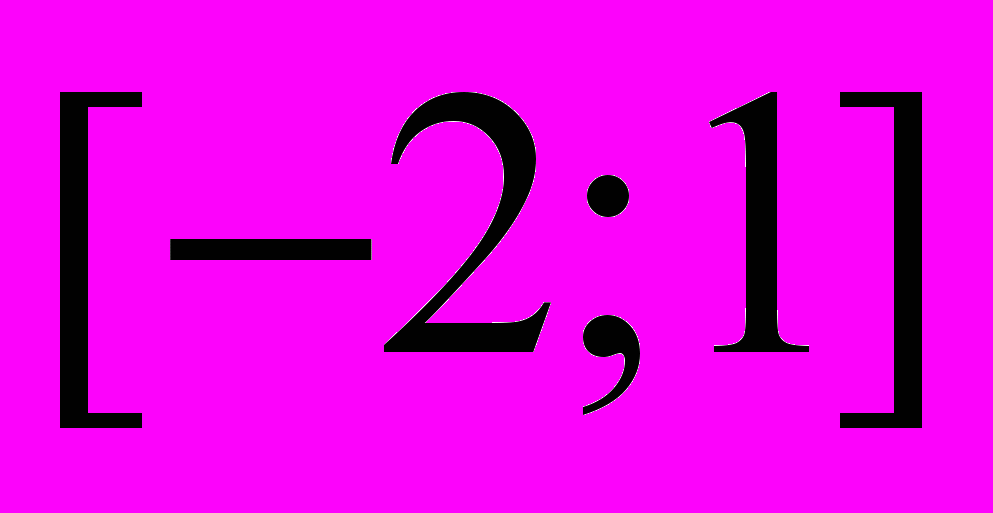в зависимости от параметра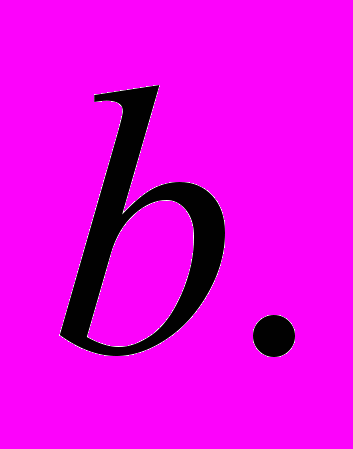

4) Найдите уравнения общих касательных к параболам 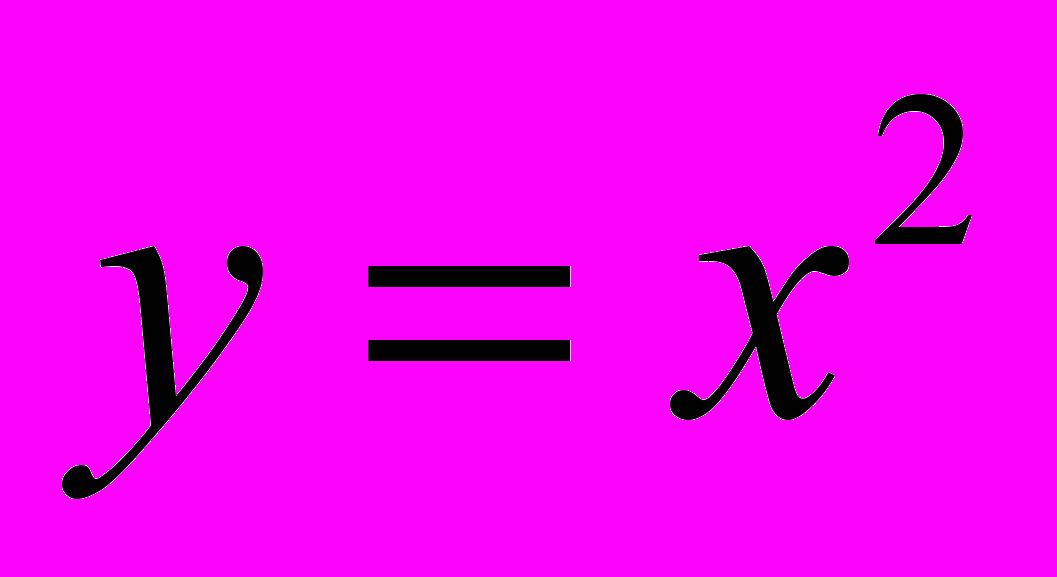и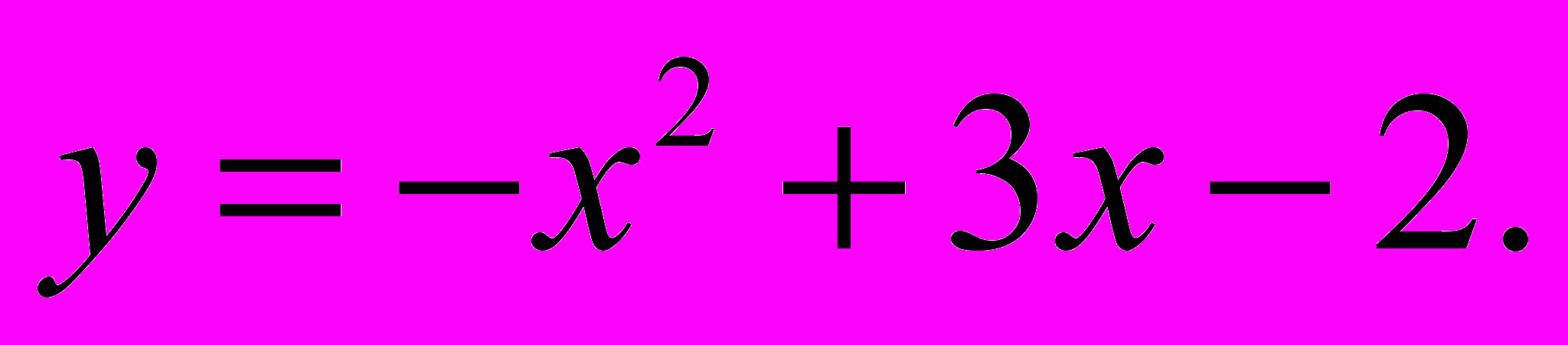

5) Длина бокового ребра правильной четырехугольной пирамиды равна Боковое ребро наклонено к плоскости основания под углом . При каком объем пирамиды будет наибольшим?