Geum.ru

Министерство образования и науки Российской Федерации Ростовский Государственный Университет

Вид материалаДокументы

Содержание


СИСТЕМА MAPLE КАК СРЕДСТВО ПОВЫШЕНИЯ КАЧЕСТВА МАТЕМАТИЧЕСКОГО ОБРАЗОВАНИЯ Мачулис В. В.
Подобный материал:
1   ...   36   37   38   39   40   41   42   43   ...   75


СИСТЕМА MAPLE КАК СРЕДСТВО ПОВЫШЕНИЯ
КАЧЕСТВА МАТЕМАТИЧЕСКОГО ОБРАЗОВАНИЯ

Мачулис В. В.

Тюменский государственный университет


marelik@rol.ru

Система Maple одна из первых и самых мощных систем символьной математики. Она создана более 20 лет тому назад канадской фирмой Waterloo Maple Inc. Главным ее отличием от известных и популярных языков программирования, ориентированных на научно-технические расчеты, таких как, например, Fortran или Pascal, является способность производить математические действия в символьном или аналитическом виде. Это отличие столь существенно, что позволило говорить о возникновении новой дисциплины – компьютерной математики. В западных странах для подобных инструментов математических вычислений на компьютере принята аббревиатура СКА (системы компьютерной алгебры), однако нам кажется более уместным название системы компьютерной математики (СКМ) ([2]), поскольку компьютерная алгебра ассоциируется только с алгеброй, а возможности таких систем значительно шире. Система Maple позволяет производить весьма сложные аналитические преобразования, зачастую недоступные «человеку с карандашом» из-за их громоздкости, содержит большое число встроенных математических функций, обладает богатыми графическими возможностями, хорошей справочной системой.

Именно возможность аналитических преобразований делает Maple и подобные ей системы наиболее эффективными для образовательных целей. Известно, что любая «численная» система решает только частную задачу, в то время как СКМ могут получить решение задачи в общем (для любого допустимого множества значений переменных и параметров) виде и без погрешности. Это дает возможность применять СКМ не только для изучения программирования, но и различных разделов математики и ее приложений.

Maple используется для обучения студентов факультета математики и компьютерных наук (ФМиКН) ТюмГУ около 10 лет. В начале этого процесса мы инициировали самостоятельную работу студентов по применению СКМ в курсовых и дипломных проектах. Затем система стала использоваться в спецкурсах и, наконец, был введен двухсеместровый факультативный курс для студентов математического отделения ФМиКН. Опыт применения Maple, в частности, в спецкурсе «Динамические системы» позволяет сделать следующие выводы:

1. Благодаря возможностям системы быстро и безошибочно производить аналитические преобразования студенты смогли познакомиться с большим числом задач, применить больше различных методов их решения. Количество пройденного материала увеличилось в 2–3 раза.

2. Богатые возможности визуализации способствовали более глубокому пониманию задачи и осмыслению результатов ее решения.

3. Система интересна большинству студентов и сама по себе. Это стимулирует ее использование в решении различных учебных и научно-исследовательских задач, а значит, способствует качественному обучению.



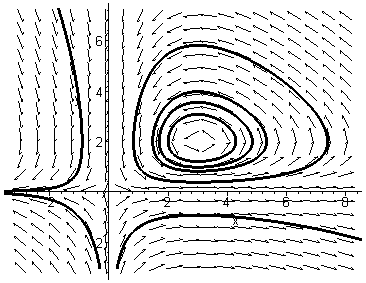
Многие задачи спецкурса «Динамические системы» требуют построения фазового портрета (с векторным полем) нелинейной системы дифференциальных уравнений. Задача, как правило, не слишком проста, к тому же громоздка и требует нескольких этапов исследования. Однако все утомительные рутинные расчеты можно переложить на Maple и сосредоточиться на анализе результата (построенном фазовом портрете). Приведем фазовый портрет системы уравнений 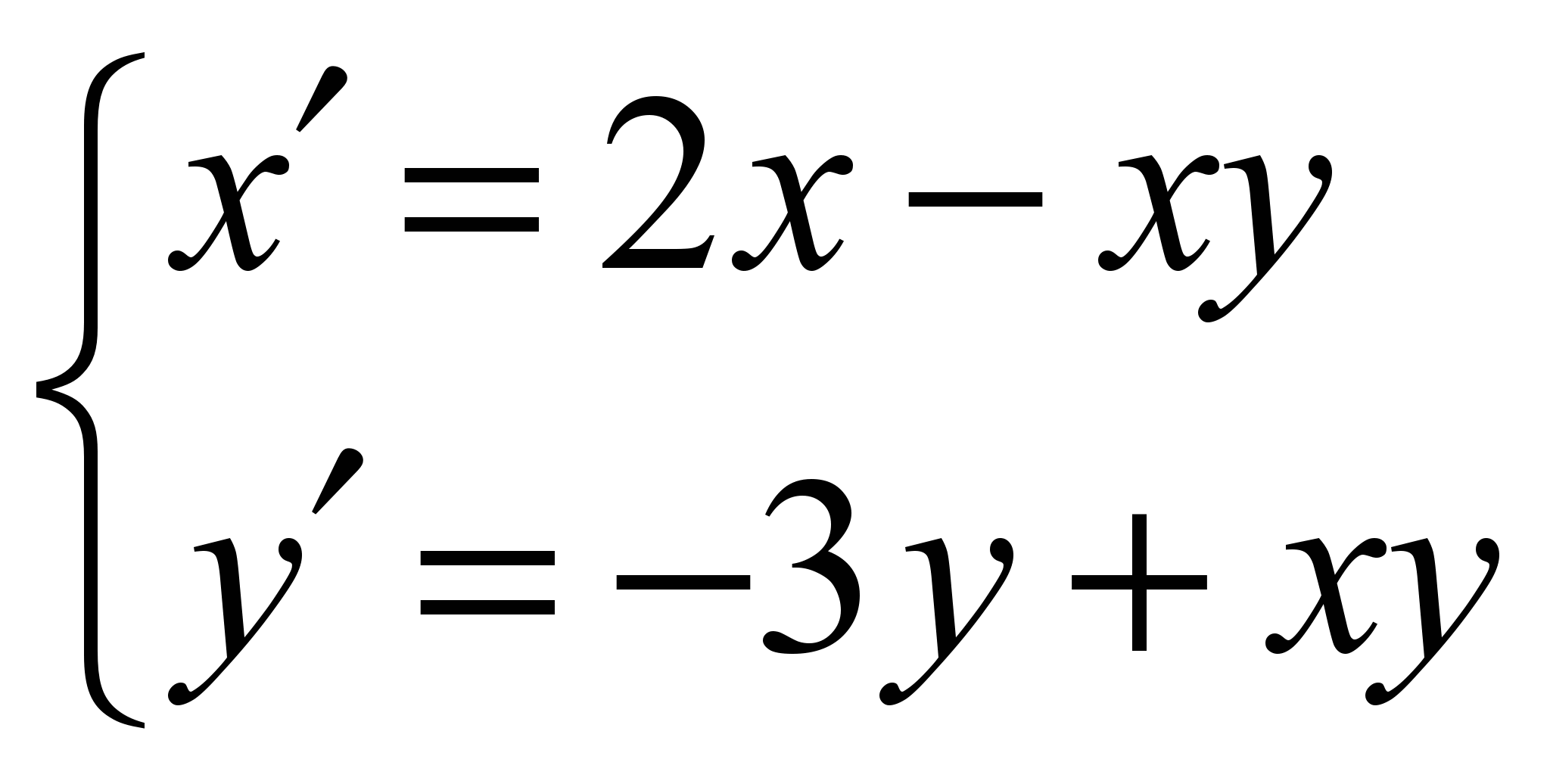, построенный с помощью Maple. На рисунке видно векторное поле на фазовой плоскости и несколько траекторий, проходящих через заданные пользователем точки. Очевидно, что эта нелинейная система имеет неподвижные точки (2:3) типа «центр» и (0;0) типа «седло». Разумеется, координаты неподвижных точек, матрицу линеаризации и другие вспомогательные результаты можно легко вывести на экран компьютера.

Оценка усвоения студентами учебного материала содержит две части: теоретическую с демонстрацией умения решать задачи вручную и «компьютерную», состоящую из нескольких программ на языке Maple, написанных студентами самостоятельно по материалу спецкурса. При этом, вопреки опасениям некоторых наших коллег, потери умения решать задачи «с карандашом» не происходит, напротив, мы отмечаем улучшение знаний, умений и навыков студентов, поэтому можем говорить о повышении качества обучения благодаря применению СКМ в учебном процессе.

Литература

1. Васильев А. Н. Maple 8. Самоучитель.: М.: Издательский дом «Вильямс», 2003. – 352 с.

2. Дьяконов В. П. Компьютерная математика. Теория и практика. М.: «Нолидж», 2001. – 1296 с.

3. Дьяконов В. П. Maple 7: учебный курс. – СПб.: Питер, 2002. – 672 с.

4. Мачулис В.В. Новые информационные технологии и изучение математики в школе и в вузе // Вестник Тюменского государственного университета №3. Тюмень: Изд-во ТюмГУ, 1999. С.237-243.

5. Мачулис В. В. Система символьной математики Maple V как средство обеспечения преемственности математического образования. // Образование на рубеже тысячелетий / Материалы Всероссийской научной заочной конференции/, Тверской государственный технический университет, г. Тверь, 2000.

6. Мачулис В. В. Дифференциальные уравнения. Основы качественной теории. Часть 1. Учебное пособие. Тюмень, ТюмГУ, 1995. – 33 с.

7. Мачулис В. В. Дифференциальные уравнения. Основы качественной теории. Часть 2. Учебное пособие. Тюмень, ТюмГУ, 1995. – 41 с.

8. Сдвижков О. А. Математика на компьютере: Maple 8. – М.: СОЛОН-Пресс, 2003. – 176 с.

9. Heck A. Introduction to Maple. – Springer, 2003. – 828 c.

10. Srtogatz S. Nonlinear Dynamics and Chaos. – Westview Press, 2000. – 498 c.

11. Wright F. Computing with Maple. – Chapman & Hall / CRC Mathematics, 2001. – 532 c.