Министерство образования и науки Российской Федерации Ростовский Государственный Университет

Вид материала

Содержание

КОНЕЧНО-ЭЛЕМЕНТНЫЙ ПАКЕТ ACELAN КАК ИНСТРУМЕНТ СТУДЕНЧЕСКОГО КОЛЛЕКТИВНОГО НАУЧНОГО ТВОРЧЕСТВА Курбатова Н.В., Наседкин А.В., Ск
Акопов О.Н., Белоконь А.В., Надолин К.А., Наседкин А.В., Скалиух А.С., Соловьев А.Н.
РЕАЛИЗАЦИЯ АЛГОРИТМОВ АФФИННЫХ ПРЕОБРАЗОВАНИЙ ПРИ ОБУЧЕНИИ КОМПЬЮТЕРНОЙ ГРАФИКЕ Куркурин Н.Д., Ахмедишев Р.Р.

Подобный материал:

1 ... 28 29 30 31 32 33 34 35 ... 75

КОНЕЧНО-ЭЛЕМЕНТНЫЙ ПАКЕТ ACELAN КАК ИНСТРУМЕНТ СТУДЕНЧЕСКОГО КОЛЛЕКТИВНОГО НАУЧНОГО ТВОРЧЕСТВА

Курбатова Н.В., Наседкин А.В., Скалиух А.С.

Ростовский государственный университет, механико-математический факультет

nvk@math.rsu.ru, nasedkin@math.rsu.ru, skaliukh@math.rsu.ru

Пакет ACELAN представляет собой конечно-элементный комплекс программ, разработанный сотрудниками кафедры математического моделирования РГУ и предназначенный для решения сложных научно-технических задач.

С помощью ACELAN можно изучать напряженно-деформированное состояние тел со сложными физико-математическими свойствами, находящихся под воздействием механических, электрических или акустических нагружений. Объекты исследования в ACELAN могут иметь составную структуру и состоять из упругих и электроупругих анизотропных тел, в том числе, контактирующих с акустическими средами. Пакет обеспечивает проведение исследований в следующих постановках: плоская деформация; плоское напряженное состояние; осесимметричные задачи, пространственные задачи для тел обобщенной цилиндрической формы.

В основу решателей ACELAN положен комплекс симметричных седловых алгоритмов и ряд оригинальных моделей [1-2].

Неопытный пользователь может достаточно легко обучиться работе в пакете, следуя специально разработанным ранее инструкциям [3]. Эти инструкции описывают пошаговое решение ряда тестовых задач, начиная от построения геометрии, задания граничных условий и материалов, проведения триангуляции, и до получения конечно-элементного решения и сопутствующих физических характеристик. Динамичное развитие пакета, пополнение его новыми модулями и возможностями требует оперативного тестирования и написания новых сопроводительных инструктивных материалов. Неопытные пользователи эксклюзивны в своей неопытности, а поэтому только достаточное их количество позволит отследить разнообразные неточности программы и формулировки алгоритмов guide–файлов, а также получить более качественные аналоги инструкций.

В этой связи в рамках продолжения работ по теме «Использование программного комплекса ACELAN для проведения лабораторных работ и студенческих научных расчетов» по программе «Развитие современных информационных технологий в процессе обучения в РГУ» было запланировано посвятить часть производственной практики студентов 5-го курса кафедры математического моделирования работе с пакетом ACELAN.

Каждому из студенческой группы «неопытных пользователей» была поставлена своя сложная задача, требующая моделирования решения в пакете, получения сравнительных результатов в родственных программах ANSYS или FlexPDE и написания собственного guide–файлa. Следует отметить, что большинство из подобранных примеров были взяты из фирменных тестов коммерческих пакетов ANSYS и FlexPDE. Поэтому данные примеры содержали описания и комментарии, которые можно было использовать как образцы при разработке собственных guide–файлов для ACELAN.

В результате студентами был подготовлен сборник инструкций по выполненным примерам. В процессе разработки guide–файлов студентами были также освоены издательский пакет LaTeX и технология создания многослойных графических панелей, а также выявлены некоторые неточности в работе интерфейса ACELAN. Проведенное комплексное тестирование следует признать чрезвычайно полезным инструментом для дальнейшего улучшения пакета ACELAN.

Подготовленный инструктивный материал является удобным методическим инструментом преподавателей кафедр, работающих в рамках программы "Создание корпоративной учебно-исследовательской кафедры математического моделирования и прикладной математики РГУ, ТРТУ и ЮРГТУ"

Список литературы

1. Акопов О.Н., Белоконь А.В., Надолин К.А., Наседкин А.В., Скалиух А.С., Соловьев А.Н. Симметричные седловые алгоритмы конечно-элементного анализа составных пьезоэлектрических устройств // Математическое моделирование. 2001. Т. 13, № 2. С.51-60.

2. Белоконь А.В., Наседкин А.В., Соловьев А.Н. Новые схемы конечно-элементного динамического анализа пьезоэлектрических устройств // Прикладная математика и механика. 2002. Т. 66, № 3. С.491-501.

3. Белоконь А.В., Курбатова Н.В., Наседкин А.В. Разработка инструкций пользователя и применение конечно-элементного пакета ACELAN в учебном процессе // Научно-методич. конф. “Современные информац. технологии в образовании: Южный Федеральный округ”. 13-14 мая 2004. Тез. докл. / Ростов-на-Дону: Изд-во ЦВВР, 2004. С. 41-44.

РЕАЛИЗАЦИЯ АЛГОРИТМОВ АФФИННЫХ ПРЕОБРАЗОВАНИЙ ПРИ ОБУЧЕНИИ КОМПЬЮТЕРНОЙ ГРАФИКЕ

Куркурин Н.Д., Ахмедишев Р.Р.

Астраханский государственный технический университет

kurkurin@astu.org, rafailka@gmail.com

В компьютерной графике широко используются методы преобразования координат, в том числе аффинные преобразования [1].

В данной работе рассматриваются частные случаи аффинных преобразований: сдвиг и поворот. При этом приводится наиболее общий случай операции поворота – кантование фигуры внутри выпуклого многоугольника.

Под кантованием будем понимать поворот внутреннего многоугольника вокруг точки касания со стороной внешнего многоугольника (без скольжения). Введем термины. Кантуемый многоугольник (фигура) – это многоугольник, который подвергаем кантованию. Базовый многоугольник – это внешний многоугольник, по сторонам которого осуществляется кантование.

Кантование представляет собой вращение кантуемой фигуры относительно её точки касания с базовой фигурой до тех пор, пока не будет зафиксирована новая точка касания [2]. Для реализации поворота фигуры используется математический аппарат аффинных преобразований. А определение точек касания двух многоугольников осуществляется методами аналитической геометрии.

Если координаты точки до преобразования (x, y), то координаты точки после преобразования (поворота точки на угол  вокруг некоторого центра вращения) определяются по формулам:

x’ = x cos - y sin

y’ = x sin + y cos

Координаты точки касания (x₀, y₀) определяются по формулам:

x₀= x – kA; y₀ = y – kB,

где: k = (Ax + By +C)/(A² + B²),

A,B,C – коэффициенты уравнения прямой, определяющей радиус вращения фигуры вокруг точки касания (x₀, y₀).

Введем некоторые ограничения:

- размеры внутреннего многоугольника не превосходят размеров внешнего, то есть все точки кантуемого многоугольника всегда находятся внутри внешнего многоугольника;

- внешний многоугольник, по сторонам которого осуществляется кантование, должен быть выпуклым;

- в данной работе мы не будем рассматривать ситуацию, при которой в какой-то момент времени внутренний многоугольник «застрянет» и дальнейшее кантование в том же направлении будет невозможно.

На рисунке 1 представлен укрупненный алгоритм кантования фигуры внутри выпуклого многоугольника.

Реализация алгоритма выполнена в среде Turbo C++.

В блоке «Инициализация» задаются исходные данные:

- описание кантуемого многоугольника (описание хранится в переменной poly=Polygon::Proper(5, 0.8, 0.8. 1);

- описание внешнего многоугольника (описание хранится в переменной borderPoly);

- представление внешнего многоугольника в виде пересечения полуплоскостей (хранится в переменной border);

- позиционирование кантуемого многоугольника внутри внешнего и координаты точки касания (переменная rotPt);

- инициализация графической системы Turbo C++.

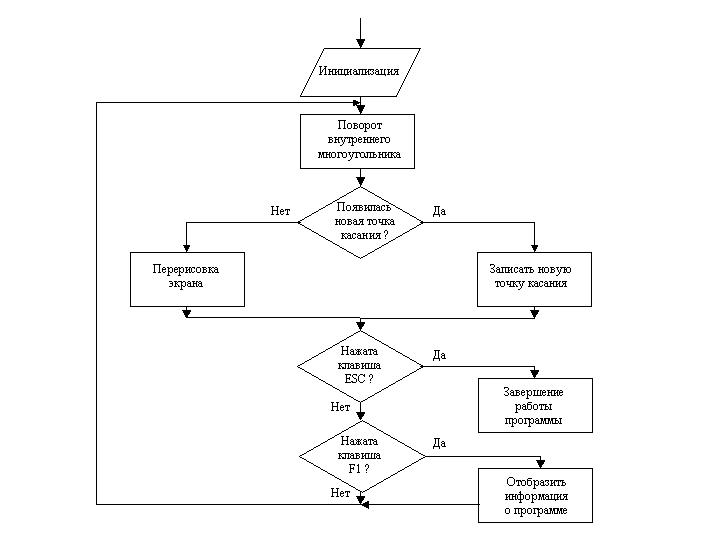
Рис. 1. Укрупненный алгоритм кантования фигуры внутри выпуклого многоугольника.

Следующие блоки реализуют основной цикл алгоритма.

В блоке “Поворот внутреннего многоугольника” производится преобразование координат для операции поворота внутреннего многоугольника (poly) вокруг точки касания (rotPt) этого многоугольника со стороной внешнего многоугольника. В следующем блоке осуществляется проверка: при повороте фигуры наступило ли событие “касания” точки внутреннего многоугольника стороны внешнего многоугольника? То есть, появилась ли новая точка касания?

Если “Да”, то в блоке “Запоминание новой точки” записываются координаты новой точки касания в переменной rotPt и выполняется следующий блок “Перерисовка экрана”.

Если “Нет”, то выполняется блок “Перерисовка экрана”.

В блоке “Перерисовка экрана” осуществляются операции:

- очистка экрана;

- вывод осей координат (ploter.OutAxes());

- вывод в графическом режиме текста подписей осей координат (ploter.DrawXLabels(), ploter.DrawYLabels());

- вывод внешнего многоугольника (ploter.FillPoly(borderPoly));

- вывод кантуемого многоугольника (ploter.FillPoly(poly));

- вывод визуальной фиксации точки касания (ploter.OutPoint(rotPt));

- копирование содержимого активной страницы в видимую страницу.

В следующих двух логических блоках осуществляются проверки нажатия клавиш ESC (Выход из программы) и F1 (Помощь), при выполнении условий соответственно выполняются блоки “Завершение работы программы” и “Отобразить информацию о программе”.

Далее осуществляется переход на начало основного цикла алгоритма.

На рисунке 2 представлено изображение на экране монитора результатов выполнения алгоритма кантования фигуры.

В качестве кантуемой фигуры описана “звезда”, в качестве внешнего многоугольника – восьмиугольник.

Текущая точка касания выделена окружностью, координаты точки касания выводятся на экран в нижней части изображения.

Блок инициализации реализован в интерактивном режиме с возможностью задания осей координат, произвольной кантуемой фигуры и произвольного внешнего многоугольника. Такая реализация позволяет студентам исследовать взаимодействие различных фигур при кантовании одной внутри другой, визуально представить процесс кантования, а также зафиксировать ситуацию, когда кантование не возможно (фигура не может “провернуться ” в рамках внешнего многоугольника, то есть фигура “застревает”, и необходима попытка обратного вращения этой фигуры).

Приведенный в данной работе алгоритм используется при обучении студентов специальности “Автоматизированные системы обработки информации и управления” по дисциплине “Компьютерная графика (программирование)”.

Рис. 2. Результаты выполнения алгоритма кантования фигуры.

Литература:

1. Порев В.Н. Компьютерная графика. – Спб.: БХВ – Петербург, 2002. – 432 с.: ил. ISBN 5-94157-139-9.

2. Бартенев Ф. Кантование кубика. // Журнал «Квант», 1982, № 6, с. 34 – 37.

Blog