«Интеграция как условие повышения качества методико-математической подготовки студентов педагогического колледжа»

Вид материала

Документы

Содержание Раздел 4 Краткий обзор истории развития методики начального обучения математике Оооо → оооооо 4 + 2 = 6

Подобный материал:

• Социально-педагогической адаптации студентов-мигрантов как условие повышения качества, 85.16kb.
• Спецкурс «Методология и методы научно-педагогического исследования» как условие становления, 72.99kb.
• Акмеология как условие повышения качества образования, 93.26kb.
• Мечникова пройдет Международная научно-практическая конференция "Экономическая интеграция, 11.08kb.
• Муниципальное дошкольное образовательное учреждение города Мурманска детский сад комбинированного, 318.78kb.
• «Внедрение инновационных технологий в воспитательно-образовательный процесс как условие, 38.44kb.
• Учебно-тематический план курсов повышения квалификации «Педагогические технологии как, 50.51kb.
• План рмо учителей физики на 2011 год Методическая тема объединения, 39.29kb.
• Основные направления научно-методической деятельности Кемеровского государственного, 150.82kb.
• Активизация мыслительной деятельности на уроках музыки с использованием занимательных, 108.99kb.

Раздел 4 Краткий обзор истории развития методики начального обучения математике

Приложение 6

Таблица 1

Итоги государственной аттестации

Учебный год	Процент успеваем.	Качество знаний	Средний балл
2004-2005г.	100%	54,6	3,9 б.
2005-2006г.	100%	68,5	3,7 б.
2006-2007г.	100%	60,9%	3,9 б.
2007-2008г.	100%	90%	4,3 б.
2008-2009г.	100%	64,3%	3,9 б.

Таблица 2.


Итоги государственной практики

Учебный год	Процент успеваем.	Средний балл
2004-2005г.	100%	4,1 б.
2005-2006г.	100%	4,3 б.
2006-2007г.	100%	4,6 б.
2007-2008г.	100%	4,6 б.
2008-2009г.	100%	4,6 б.

Приложение 7


Анкета


«Напишите, что вы можете сказать о курсе «Математика и обучение математике младших школьников» в процессе его изучения».


Вот некоторые мнения студентов.

• Мне нравится, что мы рассматриваем проблемы с разных точек зрения;
  
• Такое изучение курса позволяет глубже осмыслить связь математики с программным материалом начальных классов;
  
• Каждое задание из школьного учебника я теперь могу теоретически обосновать, что также помогает при подготовке и сдаче курсовых и государственных экзаменов;
  
• Задачи, которые мы решаем, вроде бы лёгкие, а решать их разными способами трудно. Мне надо учиться вдумываться в учебный материал;
  
• Трудно. Очень большая нагрузка;
  
• Дают много теоретических знаний, которые способствуют развитию практических умений и навыков;
  
• Иногда не справляюсь с заданиями, т.к. для меня это большой объём работ;
  
• Много самостоятельности, которая пригодится в дальнейшем;
  
• Хотелось бы выбирать форму контроля по желанию: зачёт, реферат: контрольная работа и т.д.
  
• Мои успехи в учёбе зависят от меня;
  
• Не могу сказать, что на уроках я проявляю интерес к изучаемому материалу
  
• В необходимости включения интеграции в учебный процесс я убедилась на педагогической практике;
  
• Мне интересно разрабатывать интегрированные уроки по математике для начальной школы.
  

Приложение 3

Примеры некоторых учебно-методических задач, которые позволяют выявить уровень подготовки студентов к обучению математике младших школьников в соответствии с современными педагогическими концепциями.


1. В учебнике математики для I класса (I-IV) Н.Б. Истоминой для раскрытия смысла понятия «ноль» предлагается такое задание:

Расскажи, что изменяется в каждой паре картинок. Выбери равенства, которыми можно записать эти изменения.


5-1=4

ОООО → ОООООО 4 + 2 = 6

ООООО →ОООО 9-9 = 0

ООООООО → ООООО 4 + 0 = 4

ООООООООО → 7-2 = 5

ОООО → ОООО 7 + 0 = 7

ООООООО →ООООООО 4-0 = 4

7-0=7

Можно ли утверждать, что выполнение данного задания способствует формированию представления о нуле как о числе, характеризующем пустое множество? Почему вы так думаете?

2. Проанализируйте задания по теме «Отношения» из учебника «Математика-1» (любой автор).

Объясните, на какой основе изучаются в начальной школе понятия больше, меньше, столько же.

Почему, прежде чем познакомить учащихся с числами 1 и 2, их знакомят с понятиями больше, меньше, столько же?

Как происходит знакомство с числами 1, 2?

2. Сформулируйте те строгие математические определения умножения и деления, на которых основывается их изучение в начальных классах (по двум, на Ваш выбор, образовательных программ). Подтвердите примерами из учебников то, что изучение умножения и деления в начальных классах основывается на сформулированных Вами определениях..
   
3. Во втором классе учащиеся решают такую задачу: «Составить все возможные примеры на деление (без остатка) с числами 12, 26, 4, 13, 78, 96».
   

а) Если учащиеся будут решать эту задачу методом «перебора», то как вы проверите правильность ее решения? Сколько всего примеров должно получиться?

б) Выясните, о каком отношении идёт речь в данной задаче и на каком множестве оно рассматривается.

в) Постройте граф отношения « Х делится на У без остатка» на множестве Х= { 12, 26, 4, 13, 78, 96} . Сколько стрелок он содержит? Совпадает ли ответ на этот вопрос с ответом задачи для второклассников?

Какие теоретические знания использовались при выполнении этого задания?

5. Определите виды простых задач и с помощью рисунка покажите, что решение каждой из задач связано с выделением равномощных множеств:

1. 
   Водном цехе 10 станков, а в другом – на 4 больше. Сколько станков в другом цехе?
   
2. У Маши 9 маков, а у Риты на 2 меньше. Сколько маков у Риты?
   
3. Юннаты вырастили 15 цыплят, а утят в 3 раза меньше. Сколько утят они вырастили?
   
4. Для детского сада купили 4 зелёных мяча, а красных в 3 раза больше, чем зелёных. Сколько красных мячей купили детям?
   

6. Провести анализ задачи, используя слова «необходимо» и «достаточно», а затем заменить их словами - синонимами «можно» и «нужно».

Задача. « В понедельник в магазине продали 21 телевизор, во вторник на 9 штук больше, чем в понедельник, а в среду в 3 раза меньше, чем во вторник. Сколько телевизоров продали за три дня?».

Назвать виды простых задач, входящих в данную. Дать им теоретическое и методическое обоснование.

7. Назовите 10 понятий, изучаемых в начальном курсе математики. Есть ли среди них такие, которые находятся в отношении рода и вида? Подберите или составьте сами задания, направленные на формирование у младших школьников этих понятий. Опишите возможную организацию его включения в урок.


8. Приведите по три примера вычислительных приёмов, теоретической основой которых является:

а) правило деления суммы на число;

б) конкретный смысл действий сложения, вычитания, умножения, деления;

в) связь между компонентами и результатом арифметических действий;

г) знание десятичного состава числа;

д) правило деления числа на произведение;

е) принцип образования натурального ряда чисел.

9. Тема «Отношения и соответствия» находит свое отражение во многих заданиях для учащихся. Рассмотрим несколько упражнений.

I) Составьте примеры на деление с числами 2, 4, 6, 12.

Учащиеся, как правило, выполняют подобные задания подбором. Подбор не всегда удачен для практики, ибо нет гарантии, что перебрали все возможные варианты. Если же выполнить наглядную интерпретацию в виде графа, то количество вариантов будет определено однозначно.





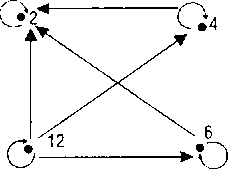
2) Составьте с числом 2 пример на деление. (2 : 2, рефлексивность отношения.)

3) Знаем, что 4 делится на 2. А «обратно»? Что можно сказать? (2 не делится на 4, антисимметричность отношения.)

4) Как бы вы закончили предложение: «Мы знаем, что 12 делится на 6, а 6 делится на 3. Тогда...» (12 делится на 3, транзитивность отношения.)

5) Решим задачу: «У Миши было 8 книг, что на 3 больше, чем у Сережи. Сколько книг у Сережи?»

Выполним наглядную интерпретацию.

У Миши на 3 книги больше, и стрелка идет к Сереже. А если от Сережи стрелку проведем обратно, то что скажем? Значит, у

него на 3 книги меньше. Выполнить рисунок рисунок:

10. Сравните процесс вашего воспроизведения теоретико-множественного определения понятия «натуральное число» до и после ответов на следующие вопросы.

Определение. Натуральное число — это общее свойство класса конечных равномощных множеств.

Вопросы.

1. Какую смысловую грань понятия описывает данное определение?

2. В результате какой операции над множествами образуются классы?

3. Из каких элементов состояло множество (дайте им характеристику), подвергнувшееся этой операции?

4. Что образуется в результате выполнения этой операции?

5. Из каких элементов (дайте им характеристику) состоят множества, называемые в определении классами?

6. Какие из явно и неявно упомянутых в определении множеств являются конечными, а какие — бесконечными?

7. Почему можно утверждать, что свойство «быть равномощным» присуще любому элементу какого-либо класса, выделившегося в результате классификации, о которой идет речь в данном определении?

8. Почему термин «равномощный» не используют для обозначения общего свойства класса, описываемого в данном определении?

9. Каким термином пользуются для обозначения общего свойства отдельно взятого класса конечных равномощных множеств? (Приведите несколько примеров.)

На данном этапе методической подготовки учителя оказываются полезными и задачи на сравнение текстов, сформулированных научным языком, и соответствующих текстов из учебников математики для детей

(см. задачи 2, 3). Задачи такого рода, требуя применения математической теории в условиях работы с учебником как средством организации учебной деятельности учащихся, способствуют не только усвоению этой теории. Они помогают студентам осознать объем и глубину знаний, которые могут по-

лучить младшие школьники благодаря материалам учебника, а также знакомят с различными способами передачи научного знания детям. Приведем примеры таких задач.

11. В учебнике математики (класса (I-III) В.В. Давыдова и его соавторов (1995) для раскрытия смысла понятия «ноль» предлагается следующее задание:

Построй отрезки по формулам.

Какая смысловая грань понятия «ноль» открывается младшим школьникам при его выполнении:

а) число 0 как характеристика пустого множества;

б) число 0 как результат измерения величины при единице измерения, которая больше измеряемой величины.

Каким образом в данном случае проявляется другой смысловой аспект понятия «ноль»?

12. Ученики начальных классов выполняли задание: «Объясни решение: 48:2 = (40 + 8) :2 = 40:2 + 8:2 = 20 + 4 = 24».

Дети объясняли решение по-разному.

Одни объяснили следующим образом: «Так как любое двузначное число можно записать в виде суммы разрядных слагаемых, где первое слагаемое обозначает количество десятков, а второе — количество единиц, и число 48 — двузначное (оно состоит из четырех десятков и восьми единиц), то

его и заменили суммой чисел 40 + 8. Получилось, что теперь надо сумму (40 + 8)разделить на число (2). Сумму разделить на число можно так: разделить на число каждое слагаемое и полученные значения частных сложить. Тот, кто решал, действовал поэтому правилу: первое слагаемое 40 разделил на число 2 и получил значение частного 20, затем разделил второе слагаемое 8 на число 2 и получил 4, результаты деления сложил 20 + 4 и получил значение частного 48:2. Оно равно числу 24».

13. В учебнике математики для начальных классов есть такое задание:

Почему можно утверждать, что это задание предлагается учащимся со следующими учебными целями:

1) раскрытие смысла вычитания на этапе анализа действий с предметами;

2) обучение построению математичес­кой модели (неравенства, равенства) наблюдаемой реальности;

3) обучение практическому и арифметическому методу решения простой текстовой задачи на сравнение величин (иначе — задачи на разностное сравнение).

14. Какие из перечисленных заданий для учащихся помогут им понять, какими почему будет первое неполное делимое в случае, если требуется 238 разделить на 7?

1. 23 : 7= ?

2.2:7 = ?

3. 21 :7 = ?

4. 238 = □ + 8

5. Сколько всего сотен (десятков, единиц) в числе 238?

6. Найди запись числа, в которой присутствие цифры 0 необязательно: 034, 304, 340. Объясни, почему в этом случае цифру 0 можно не писать?

15 . Установите соответствие между заданиями и их условными названиями, (см. табл.)

	Задания	Стрелки	Названия заданий
1	Разбей числа на две группы так, чтобы в каж- дой группе были похожие числа: 33, 84, 75, 22.13,11, 44, 59.		Задание на анализ и синтез
2	□ □□□□□□■■■И Что могут обозначать на рисунках выражения? 11 -4 10 -3 9-2 8-1 11-7 10 -7 9-7 8-7		Задание на абстрагирование и обоб- щение
3	Чем похожи и чем отличаются выражения в каждой паре? 8+6 6+6 7+8 8+2+4 6+4+2 7+3+5		Задание на классификацию
4	Выпиши ряд чисел от 1 до 9. Найди суммы тех чисел, которые соединены между собой: ' 1 1 ■ ■ I 123456789 Что ты заметил? Проверь, выполняется ли это правило для других отрезков ряда чисел.		Задание на сравнение

16. В учебнике математики для начальной школы есть задание:

Обычные и «сказочные» числа запиши в виде суммы разрядных слагаемых:

526 = УОР =

УЧФ = 720 =

801= РЧ>0 =

Примечание: для записи нуля во всех случаях применяется одна и та же цифра — 0.

Почему можно утверждать, что данное задание побуждает учащихся к абстрагированию и обобщению?

17. Младший школьник рассуждал так: «Действие, записанное в скобках, выполняется первым, значит, чтобы найти

значение выражения 6 + (3 + 1), сначала надо сложить числа 3 и 1.

Какого вида это умозаключение: индуктивное, дедуктивное или заключение по аналогии?

18. Какое требование можно сформулировать к данному условию, чтобы оно побудило школьников к индуктивному умозаключению ?

1 дес. 1 ед. — одиннадцать 1 дес. 4 ед. — ...

1 дес. 2 ед. — двенадцать 1 дес. 5 ед. — ...

1 дес. 3 ед. — тринадцать 1 дес. 6 ед. — ...

1 дес. 7ед. — ...

1 дес. 8 ед. — ...

1 дес. 9 ед. — ...

1. Составь названия чисел по данным образцам.

2. Рассмотрев образцы, вспомни правило, по которому составляется название чисел, и, воспользовавшись им, напиши названия чисел во втором и третьем столбиках.

3. Угадай правило, по которому составляются названия данных чисел.

4. Угадай правило, по которому составляются названия данных чисел, и дай названия числам, пользуясь этим правилом.