М. В. Ломоносова Социологический факультет кафедра Информатики социальных процессов А. И. Самыловский Учебно-методический комплекс
| Вид материала | Учебно-методический комплекс |
- М. В. Ломоносова Социологический факультет кафедра Информатики социальных процессов, 1371.86kb.
- М. В. Ломоносова Социологический факультет Кафедра социологии культуры, воспитания, 691.69kb.
- М. В. Ломоносова Социологический факультет Кафедра социологии культуры, воспитания, 1668.25kb.
- М. В. Ломоносова Социологический факультет Кафедра социологии культуры, воспитания, 663.83kb.
- М. В. Ломоносова Социологический факультет Кафедра социологии безопасности, образования, 809.07kb.
- М. В. Ломоносова Социологический факультет Кафедра социологии культуры, воспитания, 586.95kb.
- М. В. Ломоносова Социологический факультет Кафедра социологии безопасности Викторов, 762.25kb.
- М. В. Ломоносова Социологический факультет Кафедра социологии коммуникативных систем, 378.58kb.
- М. В. Ломоносова Социологический факультет Кафедра социологии культуры, воспитания, 837.3kb.
- М. В. Ломоносова Социологический факультет Кафедра социологии культуры, воспитания, 3044.39kb.
Ориентировочные вопросы к зачету
по «Теории вероятностей»
(весенняя зачетная сессия на первом курсе)
1. Множество элементарных исходов опыта, событие, теоретико-множественные операции над событиями. Схема опыта с равновозможными исходами. Вероятность события. Доля объектов в «генеральной совокупности», обладающих заданным свойством. Совместные и несовместные события. Теорема сложения вероятностей. Примеры применения.
2. Условная вероятность. Зависимые и независимые события. Попарная независимость событий и независимость в совокупности. Теорема умножения вероятностей. Формула полной вероятности. Формула Байеса (теорема гипотез). Примеры применения.
3. Случайная величина как математическая модель вероятностного явления. Функция распределения и функция плотности распределения вероятностей случайной величины, их свойства. Случайный вектор. Примеры применения.
4. Простейший (пуассоновский) поток событий, пуассоновская случайная величина. Показательная (экспоненциальная) случайная величина. Параметр пуассоновского потока и его оценивание по результатам измерений (по выборке). Примеры применения.
5. Схема независимых испытаний Бернулли, биномиальная случайная величина. Предельная теорема о связи биномиальной и пуассоновской случайных величин. Примеры применения.
6. Нормальная (гауссовская) случайная величина. Локальная и интегральная теоремы Муавра – Лапласа о связи биномиальной и гауссовской случайных величин. Правило «три сигма». Таблицы нормального распределения. Примеры применения.
7. Числовые характеристики случайных величин. Математическое ожидание и дисперсия, их свойства. Квантиль распределения случайной величины, “p-value”. Таблицы квантилей стандартных случайных величин. Квартиль, квинтиль, дециль, персентиль. Медиана, мода, асимметрия, эксцесс. Примеры применения.
8. Условные законы распределения случайных величин. Условное математическое ожидание. Примеры применения.
9. Неравенство Чебышёва и его использование для оценивания параметров вероятностных моделей, сравнение с использованием интегральной теоремы Муавра – Лапласа в задаче оценивания вероятности события по частоте его наступления в последовательности испытаний. Примеры применения.
10. Ковариация двух случайных величин как мера их зависимости. Коэффициент корреляции Пирсона и его свойства. Соотношение между некоррелированностью и независимостью случайных величин. Коэффициент корреляции Пирсона для линейно связанных случайных величин. Дисперсионная и корреляционная матрицы случайного вектора. Примеры применения.
11. Закон больших чисел. Центральная предельная теорема для одинаково распределенных независимых случайных величин. Предельные законы распределения выборочного среднего и выборочной доли генеральной совокупности. Примеры применения.
12. Основные задачи математической статистики. Статистическая гипотеза и этапы её проверки. Генеральная совокупность, выборка, статистика. Эмпирическая функция распределения, гистограмма. Выборочные среднее, дисперсия, ковариация, коэффициент корреляции. Статистический критерий, уровень значимости, критическая область гипотезы. Проверяемая гипотеза и конкурирующая (альтернативная) гипотеза.
Ориентировочные вопросы к экзамену
по «Математической статистике»
(зимняя экзаменационная сессия на втором курсе)
1. Использование неравенства Чебышёва и интегральной теоремы Муавра – Лапласа для оценивания параметров стохастических моделей в прикладном социологическом анализе. Примеры (оценивание доли объектов генеральной совокупности, обладающих заданным свойством).
2. Точечные оценки. Выборочные оценки математического ожидания и дисперсии, выборочная оценка вероятности, выборочная оценка «доли», выборочная оценка линейного коэффициента корреляции Пирсона. Свойства несмещенности, состоятельности, эффективности точечных оценок. Выборочные распределения. Интервальные оценки. Построение доверительных интервалов для параметров. Примеры (построение доверительного интервала для «доли»).
3. Эмпирическая функция распределения, гистограмма. Основные этапы проверки статистической гипотезы. Статистический критерий, выборка, уровень значимости, критическая область гипотезы. Примеры (проверка гипотез о виде закона распределения, о параметрах закона распределения). Исследовательская парадигма “Data Mining” в социально-экономическом анализе и пути ее реализации.
4. Нормальная случайная величина (случайная величина Гаусса) и ее использование для проверки статистической гипотезы о значении математического ожидания, для построения доверительного интервала для математического ожидания. Примеры.
5. Случайная величина хи-квадрат (Пирсона) и ее использование для проверки статистической гипотезы о виде функции плотности распределения вероятностей исследуемой случайной величины. Примеры.
6. Использование случайной величины хи-квадрат для проверки статистических гипотез об однородности выборок, о независимости двух случайных величин. Построение таблицы сопряженности «признаков». Проверка статистической гипотезы о некоррелированности двух случайных величин («признаков»). Примеры.
7. Случайная величина Стьюдента и ее использование для проверки статистической гипотезы о значении математического ожидания нормальной случайной величины, для проверки статистической гипотезы о равенстве математических ожиданий двух нормальных случайных величин. Примеры.
8. Случайная величина Фишера и ее использование для проверки статистической гипотезы о равенстве дисперсий двух нормальных случайных величин. «Односторонний» и «двухсторонний» критерии. Примеры.
9. Элементы рангового анализа результатов измерений. Критерий знаков, критерий серий, критерий Уилкоксона (Манна – Уитни) при малых выборках и «в асимптотике». Примеры.
10. Математическая модель однофакторного дисперсионного анализа. Организация базы данных. Примеры.
11. Математическая модель парной регрессии. Коэффициент детерминации. Доверительная область регрессионной прямой. Примеры.
12. Ранговые коэффициенты корреляции Спирмена и Кендалла, проверка гипотез о некоррелированности «признаков». Ранговые критерии в исследовании «панельных данных» (временных рядов). Примеры.
X. Методические указания
Отдельные подразделы программы, содержащие стандартную тематику, могут выноситься на самостоятельную проработку (в рамках сетки часов самостоятельной работы по учебным дисциплинам) с последующей отчетностью студентов в виде рефератов по таким подразделам.
Для подготовки к контрольным работам студентам рекомендуется использовать, прежде всего, лекционные материалы и материалы семинарских занятий.
При выполнении домашних заданий (эссе) как по «Теории вероятностей», так и по «Математической статистике» рекомендуется использовать примеры анализа реальных социальных ситуаций (case-studies), в больших количествах содержащиеся, например, в следующих книгах: п. 4, 5, 6 основной литературы; п.п. 5, 10 дополнительной литературы; п.п. 1, 2, 11, 13, 14, 20, 21, 23, 24, 25, 26, 27 литературы для углубленного изучения научной области.
Каждое домашнее задание (эссе) выполняется строго на листах формата А4, которые скрепляются степлером (не скрепкой !). Допускается как рукописное, так и компьютерное оформление, с использованием как одной, так и двух сторон листа. Каждое домашнее задание должно оформляться как самостоятельный документ (не следует, во избежание путаницы, объединять в одном документе, с единым титульным листом, несколько домашних заданий).
В целях текущего контроля работы студентов на каждой лекции в течение 5 – 7 минут проводится письменное тематическое тестирование (микро-контрольная работа) по материалу, как правило, предыдущих нескольких лекций. Такая работа каждым студентом выполняется строго на листе формата А5, надписывается (Ф.И.О., № группы, дата) и сдается лектору в лекционной аудитории в течение пяти минут после окончания лекции.
XI. Вероятностно-статистические таблицы
Наиболее полные вероятностно-статистические таблицы представлены в книге п.6 литературы для углубленного изучения научной области. Из книг недавних лет издания рекомендуется использовать таблицы, содержащиеся в п.п. 2, 6 основной литературы, в п.п. 5, 9, 10 дополнительной литературы, в п.п. 1, 11, 12, 13, 25, 26, 27 литературы для углубленного изучения научной области. Кроме того, все необходимые табличные значения имеются в Microsoft Excel (программная надстройка «Пакет анализа», раздел «Статистические функции» из «Мастера функций»), что подробно описано, например, в п. 7 дополнительной литературы. Ниже приводятся наиболее важные для изучения учебных дисциплин вероятностно-статистические таблицы.
Таблица 1. Биномиальная случайная величина Bi (n;p).
В таблице приведены значения биномиальных вероятностей (вероятностей для количества «успехов»
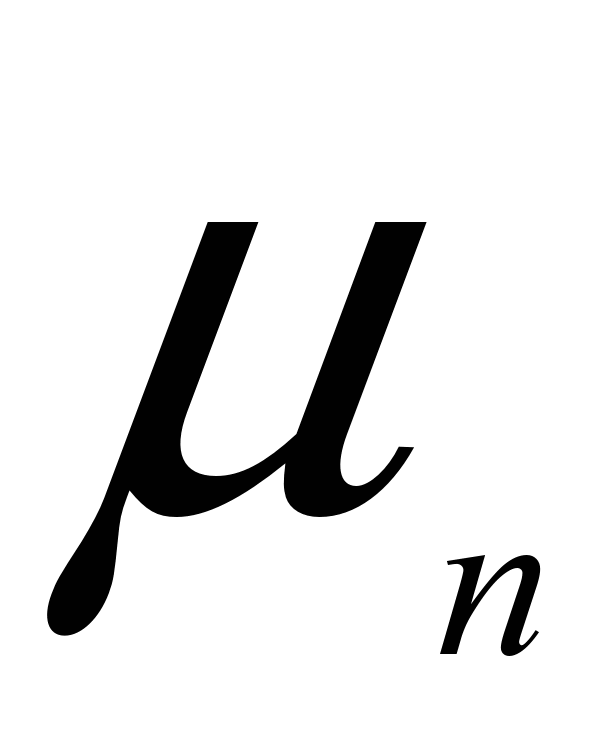 в схеме Бернулли)
в схеме Бернулли)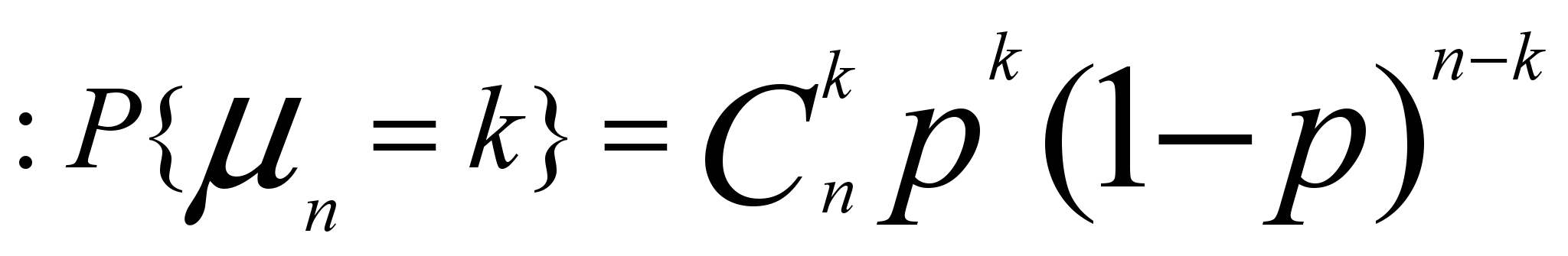 , k=0, 1, 2, …, n, при некоторых значениях количества испытаний n схемы Бернулли и вероятности «успеха» p в одном испытании (значения биномиальных вероятностей приведены с округлением до тысячных долей единицы).
, k=0, 1, 2, …, n, при некоторых значениях количества испытаний n схемы Бернулли и вероятности «успеха» p в одном испытании (значения биномиальных вероятностей приведены с округлением до тысячных долей единицы). n=5
 p pk | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 |
| 0 | 0,590 | 0,328 | 0,168 | 0,078 | 0,031 |
| 1 | 0,328 | 0,410 | 0,360 | 0,259 | 0,156 |
| 2 | 0,073 | 0,205 | 0,309 | 0,346 | 0,313 |
| 3 | 0,008 | 0,051 | 0,132 | 0,230 | 0,313 |
| 4 | 0,000 | 0,006 | 0,028 | 0,077 | 0,156 |
| 5 | 0,000 | 0,000 | 0,002 | 0,010 | 0,031 |
n=10
 p pk | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 |
| 0 | 0,349 | 0,107 | 0,028 | 0,006 | 0,001 |
| 1 | 0,387 | 0,268 | 0,121 | 0,040 | 0,010 |
| 2 | 0,194 | 0,302 | 0,233 | 0,121 | 0,044 |
| 3 | 0,057 | 0,201 | 0,269 | 0,215 | 0,117 |
| 4 | 0,011 | 0,088 | 0,200 | 0,251 | 0,205 |
| 5 | 0,001 | 0,026 | 0,103 | 0,201 | 0,246 |
| 6 | 0,000 | 0,006 | 0,037 | 0,111 | 0,205 |
| 7 | 0,000 | 0,001 | 0,009 | 0,042 | 0,117 |
| 8 | 0,000 | 0,000 | 0,001 | 0,011 | 0,044 |
| 9 | 0,000 | 0,000 | 0,000 | 0,002 | 0,010 |
| 10 | 0,000 | 0,000 | 0,000 | 0,000 | 0,001 |
n=15
 p pk | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 |
| 0 | 0,206 | 0,035 | 0,005 | 0,000 | 0,000 |
| 1 | 0,343 | 0,132 | 0,031 | 0,005 | 0,000 |
| 2 | 0,267 | 0,231 | 0,092 | 0,022 | 0,003 |
| 3 | 0,129 | 0,250 | 0,170 | 0,063 | 0,014 |
| 4 | 0,043 | 0,188 | 0,219 | 0,127 | 0,042 |
| 5 | 0,010 | 0,103 | 0,206 | 0,186 | 0,092 |
| 6 | 0,002 | 0,043 | 0,147 | 0,207 | 0,153 |
| 7 | 0,000 | 0,014 | 0,081 | 0,177 | 0,196 |
| 8 | 0,000 | 0,003 | 0,035 | 0,118 | 0,196 |
| 9 | 0,000 | 0,001 | 0,012 | 0,061 | 0,153 |
| 10 | 0,000 | 0,000 | 0,003 | 0,024 | 0,092 |
| 11 | 0,000 | 0,000 | 0,001 | 0,007 | 0,042 |
| 12 | 0,000 | 0,000 | 0,000 | 0,002 | 0,014 |
| 13 | 0,000 | 0,000 | 0,000 | 0,000 | 0,003 |
| 14 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 |
| 15 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 |
n=20
 p pk | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 |
| 0 | 0,122 | 0,012 | 0,001 | 0,000 | 0,000 |
| 1 | 0,270 | 0,058 | 0,007 | 0,000 | 0,000 |
| 2 | 0,285 | 0,137 | 0,028 | 0,003 | 0,000 |
| 3 | 0,190 | 0,205 | 0,072 | 0,012 | 0,001 |
| 4 | 0,090 | 0,218 | 0,130 | 0,035 | 0,005 |
| 5 | 0,032 | 0,175 | 0,179 | 0,075 | 0,015 |
| 6 | 0,009 | 0,109 | 0,192 | 0,124 | 0,037 |
| 7 | 0,002 | 0,055 | 0,164 | 0,166 | 0,074 |
| 8 | 0,000 | 0,022 | 0,114 | 0,180 | 0,120 |
| 9 | 0,000 | 0,007 | 0,065 | 0,160 | 0,160 |
| 10 | 0,000 | 0,002 | 0,031 | 0,117 | 0,176 |
| 11 | 0,000 | 0,000 | 0,012 | 0,071 | 0,160 |
| 12 | 0,000 | 0,000 | 0,004 | 0,036 | 0,120 |
| 13 | 0,000 | 0,000 | 0,001 | 0,015 | 0,074 |
| 14 | 0,000 | 0,000 | 0,000 | 0,005 | 0,037 |
| 15 | 0,000 | 0,000 | 0,000 | 0,001 | 0,015 |
| 16 | 0,000 | 0,000 | 0,000 | 0,000 | 0,005 |
| 17 | 0,000 | 0,000 | 0,000 | 0,000 | 0,001 |
| 18 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 |
| 19 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 |
| 20 | 0,000 | 0,000 | 0,000 | 0,000 | 0,000 |
