Учебно-методический комплекс для студентов специальностей 080801. 65 «Прикладная информатика в скс»
| Вид материала | Учебно-методический комплекс |
- Учебно-методический комплекс Для специальностей: 030501 Юриспруденция 080801 Прикладная, 498.9kb.
- Учебно-методический комплекс Для студентов специальности 080801 Прикладная информатика, 489.42kb.
- Учебно-методический комплекс для студентов специальности 080801. 65 «Прикладная информатика, 1096.4kb.
- Учебно-методический комплекс для студентов специальности 080801. 65 «Прикладная информатика, 313.43kb.
- Учебно-методический комплекс для студентов специальностей: 080801 «Прикладная информатика, 783.55kb.
- Учебно-методический комплекс по дисциплине цикла опд. Ф. 03 «Базы данных» для студентов, 341.3kb.
- Учебно-методический комплекс для студентов специальностей: 080801 «Прикладная информатика, 1213.99kb.
- Учебно-методический комплекс для специальности 080801 Прикладная информатика (в экономике), 639.9kb.
- Учебно-методический комплекс Для специальности: 080801 Прикладная информатика (в экономике), 575.12kb.
- Учебно-методический комплекс Специальность: 080801 Прикладная информатика (в экономике), 325.69kb.
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«ТЮМЕНСКАЯ ГОСУДАРСТВЕННАЯ АКАДЕМИЯ КУЛЬТУРЫ, ИСКУССТВ и СОЦИАЛЬНЫХ ТЕХНОЛОГИЙ»
Кафедра информатики и информационных технологий
Контрольная работа
по дисциплине «Теория вероятностей и математическая статистика»
Выполнил: Ф.И.О., специальность, курс, группа,
№ зачетной книжки.
Вариант
Проверил: Ф.И.О. преподавателя
Тюмень, 20__
4. Глоссарий
| № п/п | Новые понятия | Содержание |
| 1 | Предмет теории вероятностей | изучение закономерностей, возникающих при массовых, однородных опытах |
| 2 | Стохастический эксперимент | эксперимент, результат которого заранее (до его проведения) предугадать нельзя |
| 3 | Случайное событие | явление, которое может произойти или не произойти в результате стохастического эксперимента. |
| 4 | Элементарные события | события, обладающие следующими свойствами: взаимно исключают друг друга, и в результате опыта обязательно происходит одно из этих элементарных событий; каково бы ни было случайное событие А, по наступившему элементарному событию можно сказать о том, произошло или не произошло событие А |
| 5 | Достоверное событие | такое событие, которое наступает в результате появления любого элементарного события |
| 6 | Невозможное событие | событие, не наступающее ни при каком элементарном событии |
| 7 | Сумма (или объединение) двух событий А и В | событие А + В (или AB), происходящее тогда и только тогда, когда происходит или А, или В |
| 8 | Произведение (или пересечение) двух событий А и В | событие АВ (или АВ), которое происходит тогда и только тогда, когда происходит и А и В |
| 9 | Два события несовместные | если их одновременное появление в опыте не возможно |
| 10 | Событие Ā противоположно к А | если оно происходит тогда и только тогда, когда А не происходит |
| 11 | Относительная частота события А в проведенной серии экспериментов | отношение числа экспериментов, в которых событие А произошло к количеству проведенных экспериментов |
| 12 | Статистическое определение вероятности | если при увеличении числа опытов относительная частота события (A) стремится к некоторому фиксированному числу, то говорят, что событие А стохастически устойчиво, а это число обозначаемое р(А) называют вероятностью события А |
| 13 | Условная вероятность события В при условии, что событие А с ненулевой вероятностью произошло | РА(В) отношение вероятности АВ к вероятности А |
| 14 | Вероятность произведения | предполагая, что вероятности р(А) или р(В) не равны нулю, можно получить следующее: р( АВ) = р( А) • р(В | А) = р(В) • р(В | А) |
| 15 | Независимые случайные события А и В | такие события. для которых выполняется условие: р(АВ)= р(А) · р(В) |
| 16 | Полная группа событий | совокупность, при которой события H1, H2, ... , Нn удовлетворяют условиям: 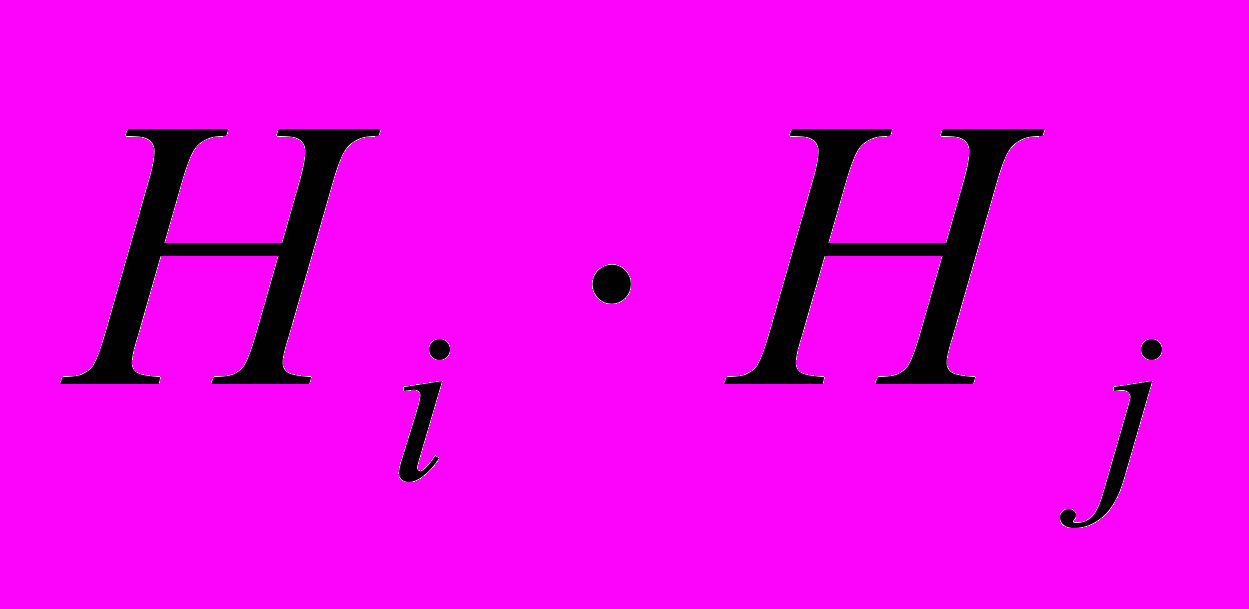 =, если i j, и =, если i j, и 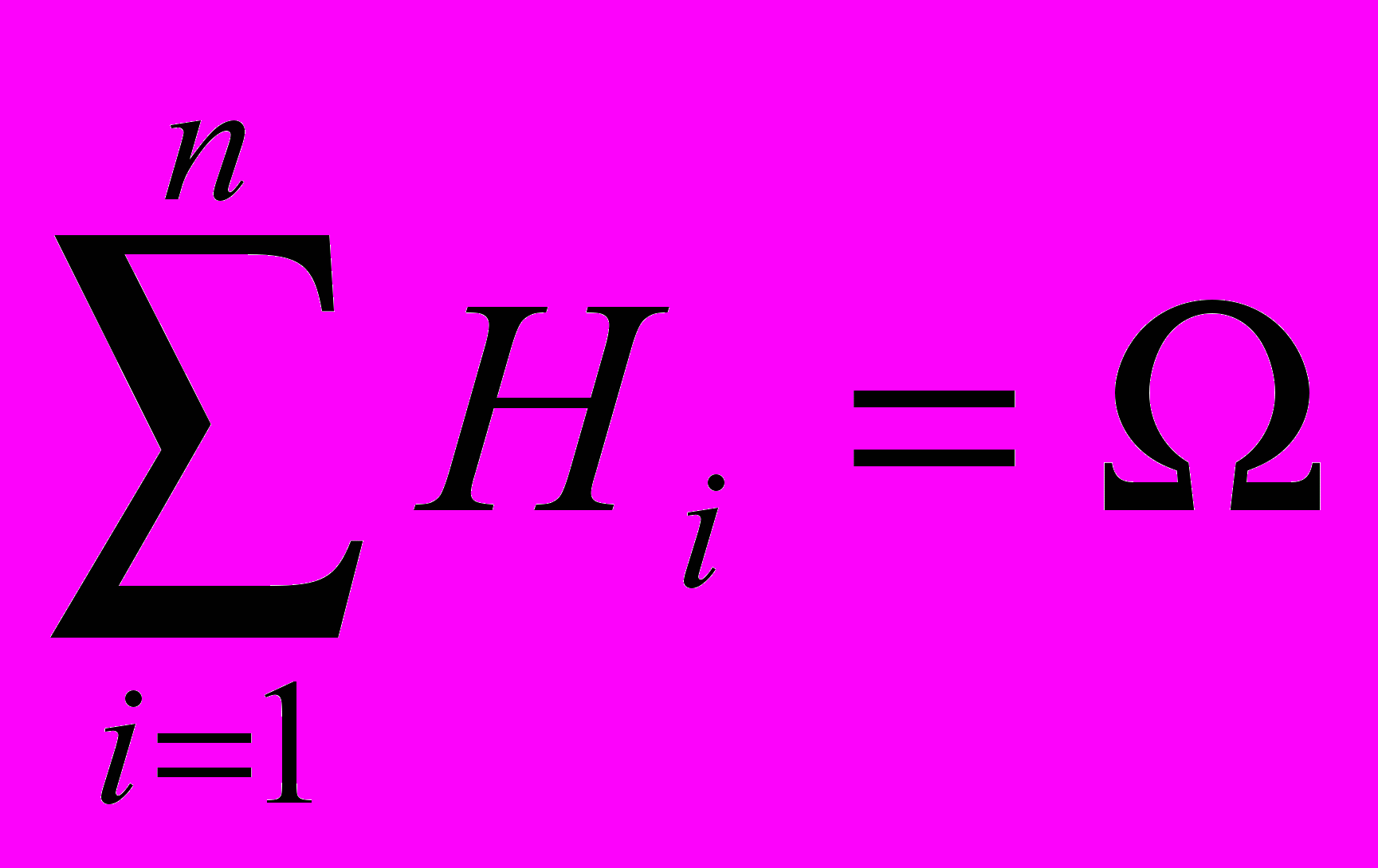 |
| 17 | Формула Байеса | 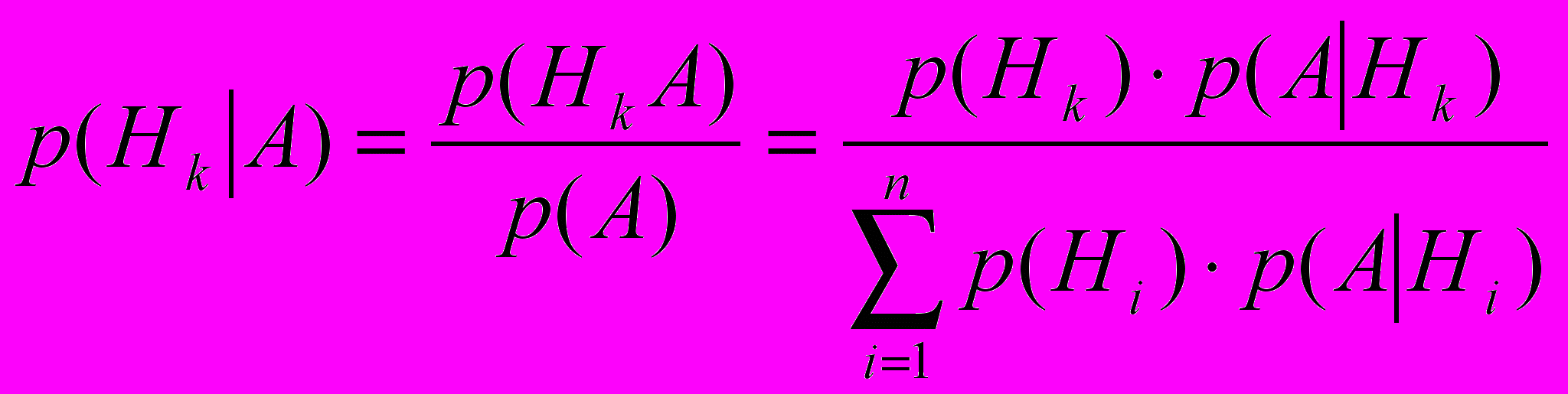 |
| 18 | Стохастический эксперимент | последовательность п независимых и однородных (одинаковых) испытаний, в результате каждого из которых может произойти события А или ему противоположное Ā с вероятностями р и q = 1-р |
| 19 | Понятие случайной величины | величина, численное значение которой может меняться в зависимости от результата стохастического эксперимента |
| 20 | Дискретная случайная величина | случайная величина, возможные значения которой образуют или конечное множество, или счётное |
| 21 | Закон распределения дискретной случайной величины | правило, по которому каждому возможному значению ставится в соответствие вероятность, с которой случайная величина может принять это значение |
| 22 | Функция распределения F(x) | функция, применяемая для задания дискретной случайной величины, равную вероятности того, что случайная величина , примет значение, меньшее х |
| 23 | Плотность вероятности | функция некоторой случайной величины, которая равна производной от её функции распределения 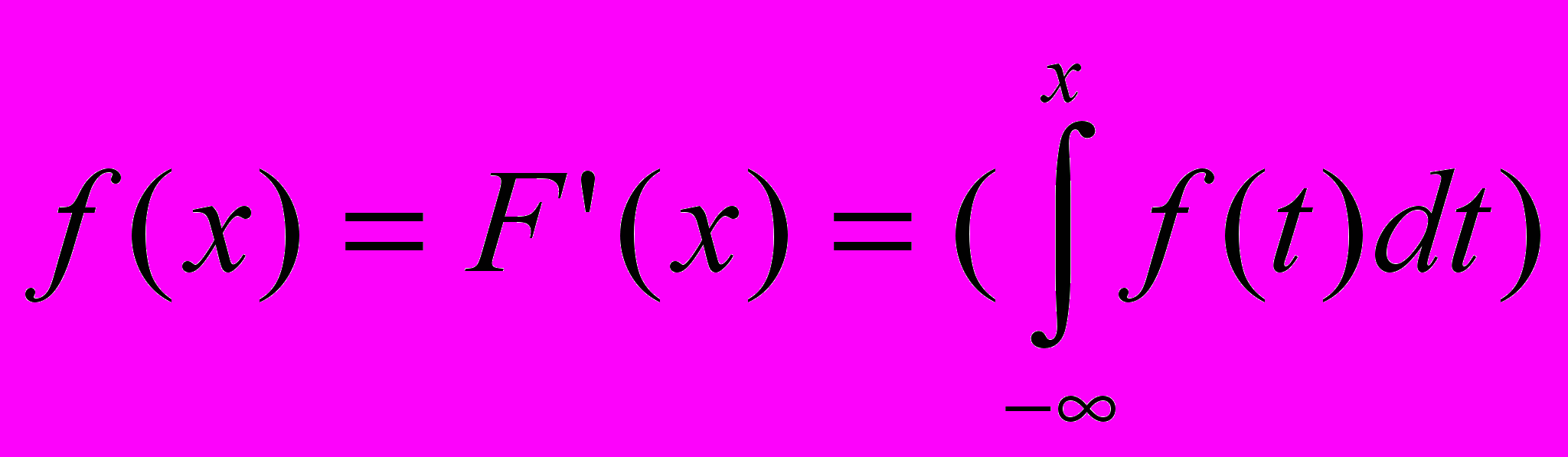 |
| 24 | Свойства плотности вероятности | плотность вероятности - неотрицательная функция; вероятность попадания случайной величины в интервал [x1, x2) равна интегралу от плотности вероятности по этому интервалу; определённый интеграл от плотности вероятности по всей числовой оси равен единице |
| 25 | Математическое ожидание дискретной случайной величины | сумма произведений всех её возможных значений на их вероятности |
| 26 | Дисперсия случайной величины | математическое ожидание квадрата отклонения случайной величины от её математического ожидания |
| 27 | Свойства математического ожидания | математическое ожидание постоянной равно самой постоянной; постоянный множитель можно выносить за знак математического ожидания; математическое ожидание суммы конечного числа случайных величин равно сумме математических ожиданий слагаемых; математическое ожидание произведения конечного числа независимых в совокупности случайных величин равно произведению математических ожиданий сомножителей |
| 28 | Свойства дисперсии | Дисперсия постоянной равна нулю; постоянный множитель можно выносить за знак дисперсии, возведя его в квадрат; дисперсия суммы (разности) конечного числа независимых в совокупности случайных величин равна сумме дисперсий слагаемых |
1 Часть заданий для контрольной работы взяты из учебного пособия Г.И. Просветова «Математика в экономике: задачи и решения». – М.: «РДЛ», 2005. – 360с.
