Учебно-методический комплекс для студентов специальностей 080801. 65 «Прикладная информатика в скс»
| Вид материала | Учебно-методический комплекс |
- Учебно-методический комплекс Для специальностей: 030501 Юриспруденция 080801 Прикладная, 498.9kb.
- Учебно-методический комплекс Для студентов специальности 080801 Прикладная информатика, 489.42kb.
- Учебно-методический комплекс для студентов специальности 080801. 65 «Прикладная информатика, 1096.4kb.
- Учебно-методический комплекс для студентов специальности 080801. 65 «Прикладная информатика, 313.43kb.
- Учебно-методический комплекс для студентов специальностей: 080801 «Прикладная информатика, 783.55kb.
- Учебно-методический комплекс по дисциплине цикла опд. Ф. 03 «Базы данных» для студентов, 341.3kb.
- Учебно-методический комплекс для студентов специальностей: 080801 «Прикладная информатика, 1213.99kb.
- Учебно-методический комплекс для специальности 080801 Прикладная информатика (в экономике), 639.9kb.
- Учебно-методический комплекс Для специальности: 080801 Прикладная информатика (в экономике), 575.12kb.
- Учебно-методический комплекс Специальность: 080801 Прикладная информатика (в экономике), 325.69kb.
1.8. Примерные вопросы для экзамена (зачета)
Дисциплина Теория вероятностей и математическая статистика
2010-2011 уч.год
Специальность: прикладная информатика в социально-культурной сфере
1. «Теория вероятностей»
1. Пространство элементарных событий. Привести три примера.
2. Операции над событиями. Несовместные события. Привести примеры.
3. Задание вероятностного пространства. Привести примеры.
4. Свойства вероятности.
5. Условная вероятность. Привести примеры. Теорема умножения.
6. Формула полной вероятности.
7. Формула Байеса.
8. Независимые события. Привести примеры.
9. Формула Бернулли. Определить вероятность выпадения ровно 1 герба при 5-ти бросаниях правильной монеты.
10. Случайная величина. Привести три примера.
11. Функция распределения и ее свойства.
12. График функции распределения для какой-нибудь конкретной дискретной случайной величины.
13. Дискретная случайная величина. Привести примеры.
14. Распределение Бернулли. Математическое ожидание и дисперсия случайной величины, распределенной по Бернулли.
15. Биномиальное распределение. Математическое ожидание и дисперсия биномиально распределенной случайной величины.
16. Распределение Пуассона. Математическое ожидание и дисперсия случайной величины, распределенной по Пуассону.
17. Непрерывная случайная величина. Свойства функции плотности.
18. Непрерывное равномерное распределение. Математическое ожидание и дисперсия случайной величины, распределенной по равномерному закону на интервале (a,b).
19. Логнормальное распределение.
20. Нормальное распределение.
21. χ2 –распределение, t- распределение, F- распределение.
22. Математическое ожидание случайной величины и его свойства.
23. Дисперсия случайной величины и ее свойства.
24. Средне-квадратическое отклонение и коэффициент вариации случайной величины.
25. Моменты, центральные моменты, абсолютные моменты случайной величины.
26. Коэффициенты асимметрии и эксцесса случайной величины.
27. Медиана, нижняя и верхняя квартили случайной величины.
28. Интерквартильный размах, мода случайной величины.
29. Квантили и процентили распределения.
30. Многомерная случайная величина.
31. Коэффициент корреляции двух случайных величин и его свойства (без доказательства).
2. «Математическая статистика»
1. Случайная выборка. Выборочные значения. Объем выборки.
2. Гистограмма. График гистограммы для какого-нибудь примера.
3. Эмпирическая функция распределения. График этой функции для какого-нибудь примера.
4. Точечное оценивание. Несмещенные оценки.
5. Состоятельные оценки. Достаточное условие состоятельности.
6. Выборочное среднее, выборочная дисперсия; выборочное средне-квадратическое отклонение; выборочный коэффициент вариации.
7. Доказать несмещенность и состоятельность выборочного среднего, как оценки математического ожидания.
8. Выборочная квантиль, выборочная медиана, выборочные нижняя и верхняя квартили, выборочная мода.
9. Выборочные коэффициенты асимметрии и эксцесса.
10. Выборочный коэффициент корреляции.
11. Доверительный интервал для математического ожидания нормального распределения.
12. Доверительный интервал для дисперсии нормального распределения.
13. Доверительный интервал для коэффициента корреляции.
14. Доверительный интервал для параметра p биномиального распределения.
15. Доверительный интервал для параметра λ распределения Пуассона.
16. Проверка статистических гипотез. Вероятность ошибки 1-ого и 2-ого рода. Уровень значимости критерия и мощность критерия.
17. Одновыборочный t-критерий.
18. Двухвыборочный t-критерий (для независимых и связанных выборок).
19. Двухвыборочный F-критерий.
20. Проверка гипотезы о равенстве параметров биномиальных случайных величин.
21. Проверка гипотезы о равенстве параметров пуассоновских случайных величин.
22. Критерии согласия χ 2, Колмогорова и Смирнова.
23. Критерии знаков и ранговых знаков.
24. Критерии для проверки гипотезы об отсутствии сдвига (для независимых и связанных выборок).
25. Проверка гипотез о независимости (для двумерного нормального и произвольных распределений).
26. Классификация методов многомерного статистического анализа.
27. Регрессионный анализ.
28. Кластерный анализ.
На экзамене в билете будет два вопроса – по одному из каждой части.
2. Контрольная работа для студентов заочной формы обучения
дисциплина Теория вероятностей и математическая статистика1
специальность 080801.65 Прикладная информатика в социально-культурной сфере
квалификация выпускника: информатик-экономист
Рекомендации по выполнению контрольной работы
- Контрольная работа выполняется в отдельной тетради.
- Первый лист оформляется как титульный (Приложение 2).
- При выполнении заданий необходимо соблюдать принятые в математике обозначения и следующие требования:
- решение каждой задачи начинается с новой страницы.
- условие задачи приводится обязательно.
- необходимые для решения задач формулы приводятся в общем виде.
- решение сопровождается кратким пояснением, объясняющим применение той или иной формулы.
- работа должна быть выполнена аккуратно, запись решения задачи должна быть четкой (читаемой).
- Сдается контрольная работа за две недели до сессии (иногородние студенты – в первый день сессии).
- Номер варианта: последняя цифра номера варианта соответствует последней цифре номера зачетной книжки, например, для номера зачетной книжки №0445-07, номер варианта №5 (15, 25, и тд.).
Задание 1. (Вариант 1-10)
В первой урне находятся а белых и b черных шаров, во второй — с белых и d черных шаров. Из первой урны во вторую переложили 2 шара. Затем из второй урны извлекли один шар. Найти вероятность того, что этот шар белый.
| Вариант | а | b | с | d | | Вариант | а | b | с | d |
| 1 | 12 | 8 | 3 | 5 | 6 | 13 | 7 | 2 | 5 | |
| 2 | 17 | 3 | 4 | 4 | 7 | 11 | 9 | б | 2 | |
| 3 | 16 | 4 | 5 | 2 | 8 | 10 | 10 | 1 | 6 | |
| 4 | 15 | 5 | 6 | 1 | 9 | 9 | 11 | 3 | 5 | |
| 5 | 14 | 6 | 5 | 2 | 10 | 8 | 12 | 2 | б |
Задание 2. (Вариант 11-20)
На заводах А и В изготовлено m% и n% всех деталей. Из прошлых данных известно, что а% деталей завода A и b% деталей завода В оказываются бракованными. Случайно выбранная деталь оказалась бракованной. Какова вероятность того, что она изготовлена на заводе A?
| Вариант | а | b | m | п |
| 11 | 15 | 25 | 80 | 20 |
| 12 | 30 | 10 | 90 | 10 |
| 13 | 20 | 5 | 85 | 15 |
| 14 | 5 | 30 | 70 | 30 |
| 15 | 5 | 15 | 60 | 40 |
| 16 | 25 | 10 | 75 | 25 |
| 17 | 30 | 20 | 55 | 45 |
| 18 | 5 | 10 | 65 | 35 |
| 19 | 30 | 15 | 95 | 5 |
| 20 | 20 | 10 | 20 | 80 |
Задание 3. (Вариант 21-30)
Вероятность поражения мишени стрелком при одном выстреле равна р. Найти вероятность того, что при n выстрелах мишень будет поражена не менее k1 и не более k2 раз.
| Вариант | p | k1 | k2 | n | | Вариант | p | k1 | k2 | n |
| 21 | 0,2 | 1 | 3 | 6 | 26 | 0,7 | 1500 | 2100 | 2100 | |
| 22 | 0,3 | 600 | 660 | 2100 | 27 | 0,3 | 3 | 6 | 6 | |
| 23 | 0,4 | 250 | 600 | 600 | 28 | 0,6 | 345 | 375 | 600 | |
| 24 | 0,5 | 5 | 7 | 8 | 29 | 0,8 | 86 | 100 | 100 | |
| 25 | 0,5 | 43 | 57 | 100 | 30 | 0,9 | 86 | 94 | 100 |
Задание 4. (Вариант 31-40
Среднее число самолетов, прибывающих в аэропорт за 1 минуту, равно m. Найти вероятность того, что за время п минут прибудут a) s самолетов; б) не менее s самолетов. Поток предполагается простейшим.
| Вариант | т | п | s | | Вариант | т | п | s |
| 31 | 4 | 2 | 2 | 36 | 4 | 8 | 4 | |
| 32 | 5 | 3 | З | 37 | 5 | 7 | 2 | |
| 33 | 6 | 6 | 4 | 38 | 6 | 6 | 3 | |
| 34 | 7 | 7 | 2 | 39 | 7 | 3 | 4 | |
| 35 | 8 | 8 | 3 | 40 | 8 | 2 | 2 |
Задание 5. (Варианты 41-50)
Произведено n независимых испытаний. В каждом из них вероятность появления события А равна р. Найти вероятность того, что отклонение относительной частоты от постоянной вероятности по абсолютной величине не превысит заданного числа ε.
| Вариант | п | p | ε | | Вариант | п | p | ε |
| 41 | 200 | 0,2 | 0,02 | 46 | 800 | 0,6 | 0,08 | |
| 42 | 300 | 0,25 | 0,04 | 47 | 900 | 0,65 | 0,09 | |
| 43 | 400 | 0,35 | 0,05 | 48 | 1100 | 0,7 | 0,05 | |
| 44 | 600 | 0,45 | 0t06 | 49 | 1200 | 0,75 | 0,04 | |
| 45 | 700 | 0,55 | 0,07 | 50 | 1300 | 0,8 | 0,02 |
Задание 6 (Варианты 51-60)
Дискретная случайная величина принимает значения xi с вероятностями pi. Найти ее математическое ожидание и дисперсию.
| Вариант | x1 | х2 | x3 | p1 | p2 | p3 |
| 51 | 1 | 5 | 3 | 0,1 | 0,7 | 0,2 |
| 52 | 4 | 7 | 1 | 0,4 | 0,5 | 0,1 |
| 53 | 6 | 2 | 8 | 0,3 | 0,2 | 0,5 |
| 54 | 3 | 6 | 7 | 0,6 | 0,3 | 0,1 |
| 55 | 8 | 7 | 3 | 0,4 | 0,2 | 0,4 |
| 56 | 3 | 5 | 7 | 0,5 | 0,1 | 0,4 |
| 57 | 4 | 7 | 5 | 0,6 | 0,2 | 0,2 . |
| 58 | 4 | 5 | 6 | 0,5 | 0,3 | 0,2 |
| 59 | 1 | 2 | 8 | 0,8 | 0,1 | 0,1 |
| 60 | 8 | 3 | 4 | 0,1 | 0,5 | 0,4 |
Задание 7. (Вариант 61-70)
Плотность распределения вероятностей случайной величины вполне определяется числами а, b, с, m. Найти m, F(x), M{X), D(X).
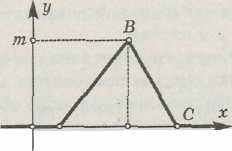
| Вариант | а | b | c |
| 61 | 2 | 3 | 4 |
| 62 | 1 | 2 | 3 |
| 63 | 1 | 3 | 4 |
| 64 | 1 | 3 | 5 |
| 65 | 2 | 4 | 5 |
| 66 | 2 | 4 | 6 |
| 67 | 4 | 6 | 10 |
| 68 | 4 | 5 | 6 |
| 69 | 4 | 5 | 8 |
| 70 | 3 | 4 | 5 |
Задание 8. (Вариант 71-80)
Плотность распределения вероятностей нормально распределенной случайной величины X имеет вид f(x) = γe –ax2+bx+c. Найти γ, М(Х), D(Х), Р(a £ Х £ β),
Р(|Х-М(Х)| <δ).
| Вариант | а | b | c | a | β | δ |
| 71 | 2 | 8 | -2 | 1 | 4 | 0,1 |
| 72 | 2 | 6 | -1 | 2 | 5 | 0,2 |
| 73 | 2 | 4 | -3 | 3 | 6 | 0,15 |
| 74 | 2 | 10 | - 4 | 4 | 7 | 0,25 |
| 75 | 2 | 12 | -5 | 5 | 8 | 0,05 |
| 76 | 1 | 2 | 1 | 1 | 2 | 0,1 |
| 77 | 1 | 4 | 2 | 2 | 3 | 0,15 |
| 78 | 1 | 6 | 3 | 3 | 4 | 0,2 |
| 79 | 1 | 8 | 4 | 4 | 5 | 0,25 |
| 80 | 1 | 10 | 5 | 5 | 6 | 0,1 |
