Задачи, предлагаемые при изучении некоторых тем 8 класса задачи, предлагаемые при изучении некоторых тем 9 класса

Вид материала

Реферат

Содержание Мировоззренческая функция Социально – педагогическая функция 1.2. Межпредметные связи Внутрипредметные связи Межпредметные связи 1.3. Воспитание интереса к математике 1.4. Развитие вычислительных и измерительных 1.5. Практическая направленность геометрии Параллельные прямые. Свойства параллелограмма. Свойства пирамиды. Поверхности и объемы тел. 1.6. Прикладные задачи в мотивации обучения 1.7. Исследовательские работы в школьном курсе Исследование площади прямоугольника данного периметра. Исследование некоторых простейших множеств точек координатной плоскости. Исследование площади прямоугольника, вписанного в треугольник. Роль и место задач в усилении прикладной направленности Задачи с практической направленностью Задачи с прикладной направленностью ... Полное содержание

Подобный материал:

• Т. М. Пахнова москва Работа с текстом при изучении и повторении лексики Предлагаемые, 292.07kb.
• Темы курсовых работ по дисциплине «Теория и методика обучения физике» Межпредметные, 19.14kb.
• Исследование содержания основных понятий менеджмента, 43.11kb.
• Анализ вторичного рынка Москвы июнь 2006, 18.57kb.
• Самостоятельная работа, ее роль в изучении физики. 15. Требования к оснащению учебного, 170.13kb.
• Использование национально-регионального компонента при изучении разделов и тем технологии, 144.43kb.
• Т. А. Развитие творческих способностей студентов-дефектологов при изучении дисциплин, 158.17kb.
• Учебное пособие адресовано ученикам 10 класса, изучающим курс информатики в обычных, 154.01kb.
• Учебная программа дисциплины дисциплина Старославянский язык, 455.54kb.
• Проекта, 43.2kb.

Управление образования Дзержинского района


«Прикладная направленность математики»


Выполнила:

учитель математики

МАОУ «СОШ №55»

Костина

Марианна Рудольфовна


Пермь 2004


Содержание


Введение ……………………………………………………………………3

Глава 1.

1.1 Мировоззренческая и социально – педагогическая

функции обучения математике……………………………………………5

1.2.Межпредметные связи как средство формирования

мировоззрения учащихся …………………………………………………7

1.3. Воспитание интереса к математике …………………………………9

1.4. Развитие вычислительных и измерительных

навыков учащихся ………………………………………………………

1.5. Практическая направленность геометрии ……………………………

1.6. Прикладные задачи в мотивации обучения …………………………

1.7. Исследовательские работы в школьном курсе……………………

Глава 2 Роль и место задач в усилении прикладной направленности обучения математике………………………………………………………….20

2.1. Основные этапы прикладного математического исследования ………21

2.2. Использование физического материала

при изучении математики ……………………………………………………23

2.3. Примеры задач прикладной направленности

с различной мотивацией ……………………………………………………..25

2.4. Пропедевтика аналитического аппарата в геометрических задачах….32

2.5. Задачи, предлагаемые при изучении

некоторых тем 8 класса ……………………………………………………….37

2.6. Задачи, предлагаемые при изучении

некоторых тем 9 класса ……………………………………………………….40

Заключение ……………………………………………………………………46

Список использованной литературы ………………………………………....47

Приложения

Результаты районного мониторинга в 2003 – 2004 учебном году ..………..48

Конспект урока в 8 классе «Вписанный угол и его величина» ....................51

Конспект урока математики в 5 классе «Восхождение на Олимп

или ещё раз об обыкновенных дробях» ……………………………………...55

Конспект урока математики в 6 классе «Немного из истории Перми»

(задачи с процентами)…………………………………………………………59

Результаты анкетирования учащихся 6«б» класса

на уровень мотивации на уроках математики ………………………………63

Творческие работы учащихся…………………………………………………62


Введение


Одной из первоочередных задач, стоящих перед школой в настоящее время, является задача дальнейшего совершенствования обучения и воспитания учащихся с тем, чтобы обеспечить наиболее полное развитие их личности и эффективную подготовку к жизни, другими словами одной из основных линий реформы современного образования является компетентностный подход к преподаванию. Под компетентностью понимается общая способность человека к высококачественной деятельности, мера включаемости человека в деятельность.


Компетенции бывают:

• Политические и социальные, способность брать на себя ответственность, участвовать в совместном принятии решений, регулировать конфликты, участвовать в функционировании и в улучшении демократических институтов;
  
• Умение жить в многокультурном обществе, понимание различий, уважение друг друга, способность жить с людьми других культур, языков, религий;
  
• Владение устной и письменной речью важно в работе и общественной жизни до такой степени, что тем, кто ими не владеет, грозит исключение из общества;
  
• Владение новыми технологиями, понимание их силы и слабости, применение
  
• Способность учиться всю жизнь, непрерывная подготовка в профессиональном плане, а также в личной и общественной жизни.
  

И компетентностный подход в преподавании заключается в формирование навыков самостоятельно применять знания в жизни. Ведь все качества, которые мы приобретаем, могут проявиться только в деятельности.


По своей компетентности выпускник общеобразовательной школы может находиться на следующих уровнях:

• Когнитивный уровень. Это приобретённые знания, которые помогают решать стандартные ситуации, это надо просто знать.
  
• Деятельностный уровень. Когда выпускник школы в состоянии поставить цель – найти средства для реализации этой цели – выполнить блок необходимых действий – получить некий результат – уметь отрефлексировать его.
  
• Личностный уровень зависит от физических и психологических качеств, которые могут ограничивать возможности; стереотипа поведения; нравственно – этических основ данного человека.
  

Для формирования компетентности нужно привить выпускнику общеобразовательной школы следующие навыки:

1. Целеполагание

2. Проектирование собственной деятельности

3. Организация продуктивной деятельности: ученика нужно помещать в зону его ближайшего развития

4. Проблемное обучение, работа с проблемой

5. Самоконтроль в ходе деятельности

6. Работа в микрогруппах, благоприятный психологический климат

7. Рефлексивная деятельность

Причем первый и седьмой пункты самые сложные и они взаимосвязаны: без рефлексии невозможно целеполагание и наоборот.

Ведь компетентный человек – это субъект своей деятельности, целеполагающий, планирующий, думающий и рефлексирующий человек.


И знание математики, в частности, рассматривается как элемент общей культуры человека. Кроме того, все области человеческой деятельности требуют овладения разносторонними знаниями и умениями, в том числе, умением применять на практике знания по математике. Это связано с процессом математизации многих отраслей науки, техники и производства. Математика превратилась в инструмент познания, учащимся надо показать, как работает этот инструмент, как им пользоваться.


Глава 1


Интерес учащихся к математическим знаниям периодически снижается. Одна из основных причин в том, что уроки математики не дают достаточно убедительного ответа на вопрос: зачем всё это нужно? Обещание благ в отдаленной перспективе не способствует усвоению абстрактных знаний.

Проблема математического образования в школе сводится не только к передаче учащимся определенной суммы знаний и навыков по предмету математики. Не менее важной задачей является реализация возможностей предмета математики в развитии личности учащихся. Важно подбирать материал, содержание которого способствует воспитанию нравственности, чувства долга, ответственности, - через раскрытие роли ученых в развитии математической науки, ознакомление с их мировоззрением и общественной деятельностью, через использование текста условия задачи и подтекстуального содержания математических задач.

В то же время роль математики в самых разнообразных сторонах жизни общества велика. Между учебным предметом и математикой, применяемой на практике, возникает определенная пропасть. Мостом между ними может и должно послужить существенное усиление прикладной направленности курса математики.


1.1 Мировоззренческая

и социально – педагогическая функции

обучения математике


Под прикладной направленностью обучения математике понимается формирование у учащихся знаний, умений и навыков, необходимых для применения математики в других учебных дисциплинах, в трудовом процессе, в быту и т.п., а в идеале – и в развитии стремления к таким применениям.

Усиление практической направленности математики – одна из основных задач, поставленных перед системой образования реформой общеобразовательной и профессиональной школы.

Превращение науки в непосредственную производительную силу ведет к тому, что знания по предметам естественно – математического цикла становятся не только базой для овладения специальными знаниями: они выступают в качестве квалифицированного требования к рабочим многих современных профессий.

В современной школе несколько нарушилась пропорция между теорией и практикой: учащиеся недостаточно владеют навыками работы с литературой, не умеют использовать полученные знания в нестандартных новых ситуациях, не могут привести примеры математических моделей и т.д. Все это свидетельствует об ослабленной практической направленности обучения математике, выполняющей две взаимосвязанные функции: мировоззренческую и социально – педагогическую.

Мировоззренческая функция реализуется в процессе изучения элементов истории возникновения математических понятий, при установлении связей математики с другими дисциплинами, в процессе составления алгоритмов и т.д.

Социально – педагогическая функция реализуется через решение задач профессиональной ориентации средствами математики, при осуществлении экономического воспитания, при решении задач оптимизации технологических процессов в современном производстве и т.д. Эти две функции очень тесно связаны между собой.

В школьном курсе математики особую ценность составляют задания, показывающие применение теоретических положений и выводов для практической жизни. Формирование способности и умений учащихся применять теоретические математические знания в конкретных ситуациях осуществляется в процессе целесообразного педагогического воздействия на протяжении длительного периода времени. Высокий уровень математической подготовки достигается в процессе обучения, ориентированного на широкое раскрытие связей математики с окружающим миром, в конкретных производственных процессах.

Прикладная направленность обучения математике предполагает ориентацию его содержания и методов на тесную связь с жизнью, основами других наук, на подготовку школьников к использованию математических знаний в будущей профессиональной деятельности, на широкое использование в процессе обучения современной компьютерной техники.

Одним из путей осуществления прикладной направленности обучения математике являются задачи, которые раскрывают применение математики в окружающей нас действительности (вычисление значений величин, встречающихся в практической деятельности; построение графиков, диаграмм и т.д.). Задачи с практическим содержанием используются в процессе обучения для раскрытия многообразия применения математики в жизни.

Этимология математических терминов и объяснение их происхождения способствует хорошему запоминанию, правильному произношению и усвоению этих терминов.

Включение в объяснение нового материала отдельных элементов из истории развития математики активизирует учащихся на организацию и проведение различных форм внеклассной работы: историко-математические кружки, математические вечера, защита математических проектов и др.

Математика обладает особыми возможностями для воспитания нравственных принципов. В процессе изучения математики у гуманитариев вырабатывается привычка к тому, что любая ошибка в вычисления или неточность в рассуждениях не останется незамеченной. Математика формирует целенаправленность, системность, последовательность. Каждый ученик должен достаточно точно и объективно оценить объем своих знаний и степень вложения в работу усилий, т.е. дать самооценку, очень важную для формирования личности школьника.


1.2. Межпредметные связи

как средство формирования мировоззрения учащихся


Проникновение математических знаний и методов в различные учебные предметы создает благоприятные условия для формирования научного мировоззрения учащихся. Учет внутрипредметных связей школьного курса математики при обучении способствует систематизации и углублению знаний учащихся, формированию у них навыков и умений самостоятельной познавательной деятельности.

• Внутрипредметные связи – это взаимозависимость и взаимообусловленность математических понятий, которые разделены лишь временем их изучения. Внутрипредметные связи представляют собой объединение преемственных, рекурсивных связей и взаимосвязей между главными линиями и идеями развития науки математики.
  
• Межпредметные связи способствуют пониманию школьниками целостной картины мира, диалектических взаимосвязей явлений природы. Межпредметные связи с точки зрения комплексного подхода обеспечивают единый подход учителей разных школьных дисциплин к формированию основ научного мировоззрения школьников.
  

Наличие межпредметных связей позволяет создать у учащихся интегративные представления о системе математических понятий и универсальных законов развития, об общих теориях и комплексных глобальных проблемах человечества. Благодаря межпредметным связям наука для учащихся представляется не только как система знаний, но и как система методов.

Рассматривая такие функциональные зависимости, как линейная, квадратичная функции и др., учитель должен вкладывать в эти понятия элементы окружающей нас реальной действительности, законов природы, наблюдаемых вокруг нас закономерностей. Через практическую направленность математики учащиеся значительно глубже и сознательнее будут усваивать изучаемый материал.

Смежные учебные предметы изучают некоторые смежные одноименные понятия, например «вектор», «график», «функция», «симметрия» и т.д. В преподавании математики должны обеспечиваться согласованность в формировании понятий, расширение их объема и углубление содержания.

Физика – предмет, где наиболее полно раскрываются разнообразные приложения математики. В тоже время физика является «поставщиком» математики, снабжая её неограниченным практическим учебным материалом. Физика школьного обучения включает в себя два основных метода исследования – экспериментальный и теоретический. Первый широко используется для получения новых знаний, а также для проверки правильности теоретических положений. Причем в процессе обработки результатов широкое применение находят математические методы. Используется и математический язык, который нашел свое выражение в физических формулах и законах. Теоретический метод в физике тоже базируется на математике, как метод исследования и метод получения новых знаний. Физическая наука переводима лишь на математический язык.

В основе изучения таких разделов физики, как механика, геометрическая оптика, теория электростатического и электромагнитного поля, лежит геометрия.

Геометрия тесно связана с химией. Большое значение имеет стереохимия, в которой устанавливается связь между свойствами органических соединений и пространственным расположением атомов, образующих молекулу данного вещества.

Глубокая прочная связь существует между геометрией и черчением, так как геометрия систематически пользуется чертежами для иллюстрации своих предложений и при решении различных задач. Черчение же, в свою очередь, пользуется законами геометрии для обоснования всевозможных построений.

Наряду со школьными дисциплинами существует связь математических дисциплин с другими науками и областями знаний человеческой деятельности:

• существенную часть минералогии составляет кристаллография, которая изучает геометрические свойства кристаллов (многогранники)
  
• тесна связь геометрии и с геодезией, задачей которой является измерение поверхности Земли. Сама геометрия изначально рассматривалась как землемерие, откуда и получила свое название. Всякого рода землемерные работы опираются на законы геометрии.
  
• в современное время большое значение имеет геометрия недр – практическая наука об определении пространственных соотношений в условиях работы под землей (шахты, туннели, метро и др.)
  
• не меньшую роль играет геометрия и в строительном деле, при сооружении зданий, мостов, каналов, при прокладке дорог, постройке всевозможных гидротехнических сооружений.
  
• геометрия связана также со станкостроением, архитектурой, производственными процессами и т.д.
  

Вопрос о путях установления межпредметных связей является одним из важнейших в проблеме совершенствования методов обучения. Наличие глубоких межпредметных связей в школьном курсе математики активизирует педагогов разных школьных дисциплин к сотрудничеству, к поиску совместных творческих проектов и взаимосвязанных проблем межпредметного содержания.

Конкретизация использования межпредметных связей в учебном процессе осуществляется с помощью поурочного планирования.


1.3. Воспитание интереса к математике


Знакомство учащихся с практическим применением изученного материала способствует воспитанию интереса к математике. Интерес – один из инструментов, побуждающий учащихся к более глубокому познанию предмета, развивающий их способности. Для воспитания и развития интереса к предмету учитель располагает в основном двумя возможностями: работой на уроке и внеклассной работой. На уроке присутствуют все ученики класса, а кружок, факультатив, внеклассное мероприятие, как правило, посещают лишь немногие. На уроках необходимо отводить место рассказам о значении математики, о математике вокруг нас, о замечательных людях, посвятивших свою жизнь математике, о связи с другими предметами и т.д. Интерес к математике усиливается, если ребята видят её связь с другими предметами. В этом плане огромное значение имеют уроки, которые ведут 2 – 3 учителя по разным предметам. Так очень интересными могут быть уроки геометрии, совмещенные с уроками физики.

• На классных часах в 5 – 6 классе родители знакомят ребят со своей работой, рассказывая при этом, где и как у них применяется математика. Учащиеся получают задание совершить «экскурсию» на производство к своим родителям и затем написать реферат «Математика в профессии моих родителей», в котором должна содержаться задача с производственным содержанием, составленная учеником и её решение. Защита рефератов может быть проведена на совместных собраниях с родителями. Вначале слово предоставляется ученику, а затем его рассказ дополняет и оценивает мама или папа. Окончательную оценку реферата выдает комиссия, в состав которой входят другие родители, учащиеся, учитель. Комиссия учитывает сложность составленной задачи, красоту её решения. Во время экскурсии ребята стараются детально разобраться в сути дела, тщательно собирают данные для составления задачи, причем нередко бывают на работе родителей не один раз. Такая работа способствует развитию творческих способностей учащихся, при этом у них появляется и укрепляется чувство уважения к своим родителям, затрагиваются и вопросы профориентации. В 7 – 8 классах ребята могут писать рефераты на темы «Математика вокруг нас», «Математика за страницами школьного учебника», либо сочиняют сказки, рассказы на математические темы.
  
• Игра – спутник человеческой жизни от колыбели до глубокой старости. «Игра – путь детей к познанию мира, в котором они живут и который призваны понять», - писал А.М.Горький. в играх укрепляются и развиваются чувства товарищества, солидарности, честности, правдивости и другие качества. Игра является хорошей союзницей не только в воспитании детей, но и в обучении их, поэтому учителям необходимо периодически пользоваться играми или вводить элементы игры и на уроках, и во внеурочное время. Познание же математики через игры прививает к ней любовь, переходящую иногда в потребность серьезно заниматься этой наукой.
  

1.4. Развитие вычислительных и измерительных

навыков учащихся


Первая математическая дисциплина, изучаемая в школе, - арифметика имеет огромное теоретическое и практическое значение, так как объект её изучения – число – охватывает широкий круг предметов и явлений. Задача учителя заключается, в первую очередь, в том, чтобы научить детей основам арифметики, её теории и практики. Учитель приближает преподавание арифметики к разрешению жизненно важных вопросов и воспитывает у учащихся умения и навыки, которые должны найти непосредственное применение в различных видах практической деятельности.

• При выполнении операций над целыми и дробными числами проводится: прикидка вычислений, проверка вычислений, вычисления на счетах, вычисления с помощью таблиц, процентные вычисления и т.д.
  
• При работе с приближенными вычислениями детям напоминается о том, что числа, с которыми мы встречаемся в газетах, справочниках, задачниках, на упаковочных материалах, почти все являются приближенными. Используется округление, деление с остатком, нахождение среднего арифметического, приближенного частного, абсолютной и относительной погрешности.
  
• В процессе изучения математики учащиеся должны знать единицы измерения величин, соотношения между ними и уметь выполнять действия над ними.
  
• Для овладения системой мер следует предлагать учащимся различные упражнения, например: найти вес различных жидкостей (керосин, масло, ртуть и т.д.) по данным объемам и удельным весам.
  
• Полезно ознакомить учащихся с действительными размерами известных им предметов, со средними скоростями пешехода, велосипедиста, автомобиля, поезда и т.д.
  

Вычислительные и измерительные задания формируют у учащихся навыки, необходимые в их будущей трудовой деятельности. Такая работа осуществляется на практических занятиях по математике, на вычислительных практикумах, лабораторных работах по измерению геометрических величин, в процессе проведения приближенных вычислений, в ходе измерительной работы на местности и др.

В учебном материале по математике описываются различные измерительные инструменты: астролябия, рейсшина, штангенинструмент и т.д. Это дает возможность активизировать работу учащихся по формированию вычислительных навыков, навыков измерений и работы с единицами измерения.


1.5. Практическая направленность геометрии


Любой учебный материал по геометрии имеет практическую направленность.

• Теоремы о равенстве треугольников. Признак равенства треугольников по трем сторонам является теоретической основой «жесткости» треугольника, что широко используется в технике при конструкции мостов, подъемных кранов и т.д.
  

• Параллельные прямые. На уроках целесообразно показывать методы построения таких прямых при помощи чертежного треугольника, рейсшины, а также построения на местности параллельных прямых с помощью экера – проведением перпендикулярных прямых к одной и той же прямой.
  

• Свойства параллелограмма. Из всех плоских геометрических фигур самой распространенной является прямоугольник, так как он имеет две оси симметрии. Наиболее удобная форма сельскохозяйственных полей для обработки сельскохозяйственными орудиями есть форма прямоугольника.
  

• Свойства пирамиды. При пересечении пирамиды плоскостью, параллельной основанию, получается сечение, площадь которого прямо пропорциональна квадрату расстояния от её вершины. Это обстоятельство служит теоретическим объяснением зависимости между силой освещения и расстоянием от источника света, находящемся в вершине пирамиды. При удалении площадки (основания) на расстояние, вдвое большее от вершины, площадь увеличится вчетверо, а количество световой энергии, приходящейся на единицу площади, станет вчетверо меньше. Таким образом, сила освещения обратно пропорциональна квадрату расстояния от источника света. Пользуясь этим законом, современная астрономия определила расстояние до самых отдаленных объектов Вселенной, расстояния, которые луч света проходит за многие сотни тысячелетий.
  

• Поверхности и объемы тел. При их вычислении следует обращать внимание учащихся на тот факт, что при изменении линейных размеров тела поверхность его изменяется пропорционально квадрату, а объем – кубу этих размеров.
  

Занятия по геометрии должны сопровождаться практическими работами с привлечением всех учащихся. Это могут быть все виды моделирования, различные землемерные работы, измерение поверхностей и объемов предметов техники, домашнего обихода, хозяйственных построек и т.д.


1.6. Прикладные задачи в мотивации обучения


В преподавании математики очень важна мотивационная сторона.

• Математическая задача воспринимается учащимися лучше, если она возникает как бы у них на глазах, формулируется после рассмотрения каких-то физических явлений или технических проблем.
  
• Ещё один прием мотивации – обращение к историческим событиям, создающее эмоциональный подъем в классе. Даже самая неинтересная тема способна увлечь школьников, если учитель сумеет связать с ней такие факты, которые вызывают светлое чувство у слушателей.
  

Ссылка на историю всегда вызывает у учащихся интерес, а если еще задача предложена из какого-либо древнего источника со своеобразной формулировкой, то это ещё больше стимулирует школьников к её решению.

• С большим интересом воспринимаются задачи, вызывающие споры. Такие задачи сначала кажутся учащимся простыми, и ответы на них следуют немедленно. Однако ответы оказываются неодинаковыми, возникает спор. Рассудить спорящих может только убедительно изложенное решение.
  
• Важной особенностью прикладных математических задач является применение размерных величин.
  

Наблюдение за размерностью величин в процессе решения задачи позволяет выявить ошибки в этом решении. Например, если a и b – длины, а в процессе решения появится выражение a² - 2b, можно сразу сделать вывод, что допущена ошибка.

• Другая особенность прикладных задач состоит в постоянном стремлении довести решение до числа, причем «круглые» ответы здесь весьма редки. Задачи же, применяемые в школьной практике, порой создают у учащихся представление о том, что «некруглость» ответа является признаком его ошибочности.
  
• Существенным в прикладной направленности обучения математике является привитие методов самоконтроля
  

Если задача решена в буквенном виде, то для контроля применяется проверка размерности полученного выражения; исследование поведения решения, когда параметры задачи обращаются в нуль или значительно возрастают, или принимают какие-либо иные характерные значения, при которых решение можно получить из наглядных соображений. Если получено численное значение решения, то для контроля можно сравнить его с результатом грубой прикидки, с оценкой, полученной «по здравому смыслу». Предварительная прикидка ответа вообще весьма полезна. Все это помогает не только проконтролировать ответ, но и развить правильную интуицию.


1.7. Исследовательские работы в школьном курсе


Существенную роль в усилении прикладной и практической направленности и одновременно в развитии способностей учащихся к самостоятельным исследованиям играют задания, выполнение которых представляет собой относительно завершенный исследовательский цикл: наблюдение – гипотеза – проверка гипотезы. В качестве таких заданий целесообразно использовать исследовательские работы. Это одно из средств повышение активности школьников.

Часть исследовательских работ может быть реализована не только на уроке, но и в качестве домашнего задания. В последнем случае на уроке обсуждаются результаты, полученные учащимися дома.

Выполняя исследования, ученики также развивают и навыки использования инструментов.

• Понятие функции формируется в 7 классе на основе понятия зависимости. Этот этап крайне важен. Ведь мировоззрение формируется путем акцентирования прикладных аспектов обучения, связи математики с жизнью, с другими предметами. Выполняя исследовательские работы, ученики на конкретных, самостоятельно установленных зависимостях усваивают проблематику, которая затем будет являться ядром всей функциональной линии курса математики курса средней школы.
  

Первая работа проводится непосредственно перед изучением темы «Функция» или в начале этой темы.


Работа № 1. Исследование площади прямоугольника данного периметра.

Периметр прямоугольника 24см, а его основание х см. Задайте формулой зависимость площади S (см²) прямоугольника от х.

1. Заполните таблицу

х	2	3	4	5	5,5	5,8	5,9	6	6,1	6,2	6,5	7	8	9	10
S

2. При каком значении х у вас получился прямоугольник наибольшей площади? Какова наибольшее из полученных значений S? Выберите сами два каких-либо допустимых значения х и вычислите соответствующие им значение S.

3. Удалось ли вам получить значение S, большее чем найденное ранее? Какую гипотезу можно высказать на основании проведенного исследования о форме прямоугольника наибольшей площади, имеющего данный периметр?


Работа № 2. (Лабораторная) Построение графика зависимости высоты столба жидкости в сосуде от объема жидкости.

Приборы и материалы: ведро стандартное, банка литровая, линейка.

1. налейте в ведро 1 л воды. Измерьте высоту столба жидкости в ведре. Запишите полученный результат в таблицу

Объем воды V	1	2	3	4	5	6	7	8	9	10
Высота столба h

2. Постройте график зависимости h от V.

3. Какой график получился: прямолинейный или криволинейный?

В отличии от других работ, которые могут быть как классными, так и домашними, эта работа выполняется лучше в домашних условиях. А на уроке обсуждаются её результаты. Анализ различий в графиках, полученных школьниками, использовавших ведра различной формы, послужит развитию физических представлений о равномерных и неравномерных процессах. Работу целесообразно провести при изучении темы «График»


Работа № 3. Исследование некоторых простейших множеств точек координатной плоскости.

Данная работа наряду с развитием представлений о координатной плоскости осуществляет пропедевтику темы «Линейное уравнение с двумя переменными». Его можно предложить непосредственно перед изучение темы. Тогда результаты можно будет использовать для проблемного изложения темы «График линейного уравнения с двумя переменными»

1. Постройте на координатной плоскости несколько точек, у которых сумма абсциссы и ординаты равна 10 (при выборе координат используйте и отрицательные числа)

2. В чем особенность расположения построенных точек?

3. Выскажите гипотезу о том, как располагаются на плоскости все точки, обладающие таким свойством.

4. Возьмите несколько точек, у которых сумма абсциссы и ординаты: а) больше 10; б) меньше 10.

5. выскажите гипотезу об их расположении относительно предыдущего задания.

Работа № 4 График расстояния


Эта работа имеет одной из целей формирование отчетливых представлений о различии между понятиями расстояния между точками и пройденного пути.

Туристы отправились на байдарках по течению реки из пункта А в пункт В со скоростью 5 км/ч. После 3 ч пути они сделали остановку на 1 ч, а затем поплыли дальше со скоростью 6 км/ч. На рисунке изображена схема маршрута туристов, на которой отмечены отрезки пути длиной в 1 км.




1. Определите на схеме точку, в которой находились туристы через 1 ч после отправления из А

2. Найдите (по прямой) расстояние от этой точки до пункта А

3. Запишите полученный результат в таблицу

Время t	0.5	1	1.5	2	2.5	3	3.5	4	4.5	5	5.5	6	6.5	7	7.5	8
Расстояние d

4. Выполните указанные действия, выбирая приведенные в таблице значения t

5. постройте график зависимости d от t.

Далее школьникам предлагается ответить на вопросы о наибольшем и наименьшем значении, о возрастании и убывании и т.п.


Работа № 5 Исследование площади прямоугольника, вписанного в треугольник.


Работа осуществляет пропедевтику геометрических задач на экстремум. Необходимые для строго обоснования гипотезы знания учащиеся получат в курсе следующего класса. Трудно предположить, что они все ещё будут помнить эту работу, но вместе с другими заданиями она призвана подготовить их мышление к адекватному восприятию соответствующего материала.

В треугольник АВС, основание которого равно 10см, а высота 8 см, вписано несколько прямоугольников различной высоты, имеющих две вершины на основании, а две другие на боковых сторонах треугольника.



1. Учитывая, что можно построить сколько угодно таких прямоугольников, постройте самостоятельно прямоугольники с высотами, указанными в таблице.

2. Измерьте основание каждого прямоугольника и его площадь, результаты занесите в таблицу.

Высота h	0,5	1	2	3	3,5	4	4,5	5	6	7	7,5
Основание a
Площадь S

3. При каком значении h получился прямоугольник наибольшей площади? Какова его площадь?

4. Сравните высоту, основание и площадь этого прямоугольника соответственно с высотой, основанием и площадью треугольника АВС

5. Какую гипотезу можно высказать в результате этого исследования?

• В 8 классе школьники изучают тему «Неравенства». Материал, которой позволит дать сформулированным гипотезам строгое обоснование.
  

Работа № 6.


При обсуждении результатов этой работы следует поставить перед учащимися вопрос о «поведении» графика при неограниченном увеличении значений х, осуществляя пропедевтику понятия предела.


К числителю и знаменателю дроби 1/2 прибавляется одно и тоже положительное число х.

1. Заполните таблицу, округляя значение дроби

х	0	1	2	3	4	5	6	7	8	9	10
1 + х 2 + х

2. Постройте график функции у = 1 + х при х  0

2 + х

3. Как изменяется значение правильной дроби 1/2 при возрастании значений х?

4. Проведите аналогичное исследование, взяв неправильную дробь, например 5/2.

5. Сформулируйте гипотезу об изменении значений правильной и неправильной дробей при увеличении числителя и знаменателя на одно и тоже положительное число.

• При изучении тригонометрического материала по некоторым программа в 9 классе, по другим в 10 классе, очень познавательна следующие работы. Они также ориентированы на развитие стереометрических представлений учащихся
  

Работа № 7.


Для изготовления водопойного желоба на животноводческой ферме решили сбить три одинаковые доски длиной 4 м и шириной 25 см каждая. Вместимость (V) желоба равна произведению площади трапеции АВСД на длину желоба.




1. Задайте формулой зависимость вместимости желоба от угла  при основании ВС трапеции АВСД.


2. Заполните таблицу

 (в градусах)	90	100	110	120	130	140	150
объем

3. При каком из указанных в таблице значений  получится желоб наибольшей вместимости?

Работа № 8


Учет уложенных в штабель бревен ведется с использованием коэффициента полнодревесности , который равен частному от деления объема древесины от объема самого штабеля. Найдите коэффициент полнодревесности  прямоугольного штабеля, в основании которого 4 бревна, а число бревен по высоте равно 3. (Все бревна считать одинаковыми цилиндрами радиуса R)




Зависит ли  от числа бревен в прямоугольном штабеле?

А если штабель будет треугольным, в основании которого n бревен?

Рассмотрите случаи, когда n = 3; 4.


Работа № 9 «Определение числа атомов, приходящихся на ячейку кристаллической решетки»


Выполнение такой работы развивает пространственное представление учащихся, расширяет и углубляет знания о свойствах параллельных и перпендикулярных плоскостей, о понятиях симметрии и параллельного переноса, помогает объяснить многие явления из химии и технологии материалов, облегчает решение многих задач.




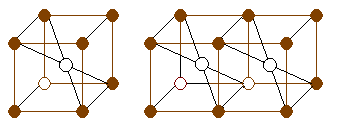
Определите средне число атомов, приходящихся на одну элементарную ячейку. В случае, когда она одна – 9, для двух смежных 14 : 2 = 7.

Как будет изменяться количество атомов с увеличением числа ячеек? Имеет ли оно предел?

Количество ячеек постепенно наращивается, сначала в один слой, потом в несколько слоев.

Если обозначить через k количество ячеек в ряд, то нетрудно вывести формулу числа атомов в ряду N = 4(k + 1) + k



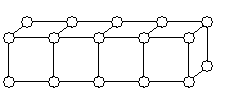
При увеличении числа слоев, обозначим это количество l. Формула числа атомов выводится N = 3kl + 2l + 2k + 2.



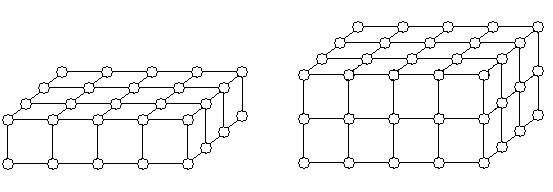
При наращивании слоев в третьем измерении m формула приобретает следующий вид: N = 2klm + lm + km + kl + k + m + l + 1.

Если тело кубической формы, т.е. k = l = m, N = 2k³ + 3k² + 3k + 1


Исследовательские работы удачно вписываются в общую структуру учебного процесса, позволяя связать между собой отдельные вопросы курса алгебры, геометрии, физики, химии, а также осуществить достаточно серьезную пропедевтику некоторых вопросов из школьного курса начал анализа.