Задачи, предлагаемые при изучении некоторых тем 8 класса задачи, предлагаемые при изучении некоторых тем 9 класса

1   2   3   4

Интересующими нас величинами являются площадь поверхности, длина швов и стоимость изготовления. Анализируя модель, учащиеся выясняют, что боковые грани – прямоугольники, верхнее и нижнее основания – квадраты, общая длина швов равна сумме периметров обоих оснований и длины бокового ребра.

2. Создание математической модели. Рассматриваемый параллелепипед определяется длиной стороны основания a и высотой h. В силу формулы V = а²h имеем h = V : a² . Поэтому за искомую величину можно принять длину стороны основания. Обозначим её буквой х, площадь поверхности S(x), общую длину швов l(x), стоимость изготовления C(x). Нетрудно видеть, что S(x)= 2х² + 4V/х, l(x)= 8х + V/х², C(x)=  l(x) +  S(x),где  - стоимость сварки,  - стоимость жести.

C(x) = (8х + V/х²) + (2х² + 4V/х).

Для контроля проверяем, что правая часть имеет правильную размерность. Раскрывая скобки, получаем

C(x)= 2х² + 8х + 4V/х + V/х².

Итак, математическая постановка задачи может быть сформулирована следующим образом: для функции C(x), 0 х  , требуется найти точку, при которой она принимает наименьшее значение.

3. Решение и исследование математической задачи. Подставив заданные значения , , V, получим выражение C(x)=400х² + 800х + 200/х +25/х². Найдем производную: C'(x)=800х + 800 - 200/х² – 50/х³ =800/х³ (х⁴ + х³ – х/4 – 1/16) = 800/х³(х – ½)(х + ½)³.

Отсюда видим, что при 0 х   производная меняет знак при переходе через точку х = ½ с минуса на плюс. Поэтому ответом является х = ½, т.е. 0,5 м.

Для подтверждения оптимальности результата полезно подсчитать стоимость бака при различных значениях х.

4. Интерпретация математических результатов. Проведенное исследование позволяет дать следующую рекомендацию. Оптимальные размеры для изготовления бака: длина стороны основания 0,5 м, высота бака 1 м. Стоимость изготовления при этом составит 1000 рублей.


Решение подобных задач полезно во многих отношениях:

1. учащиеся овладевают приведенной схемой решения прикладных задач
   
2. такое решение способствует развитию прикладной математической культуры, выработке необходимых навыков применения математических знаний и способов действия при решении практических задач
   
3. происходит знакомство учащихся с ролью математики в практической деятельности
   
4. решение задач на оптимизацию служит экономическому воспитанию учащихся.
   

Основными принципами работы над задачей являются:

1. методическая обработка задачи согласно целям обучения и требованиям к системе задач
   
2. обучение учащихся на каждом этапе процесса решения задач
   
3. использование при решении задач методов, близких к тем, которые встречаются в практической деятельности (поиск, исследование, правдоподобные рассуждения и интуиция, использование справочников, таблиц и т.д.)
   
4. рассмотрение нескольких способов решения и обсуждение оптимального варианта.
   

Итак, задачи могут выступать основным средством усиления прикладной направленности обучения математике, если к ним правильно подходить.


2.2. Использование физического материала

при изучении математики


В курсе физики 7 – 9 классов изучаются помимо известной формулы движения s = vt, например, такие:

1. m = V, где m – масса,  - плотность, V – объем

2. p = F / S, где p – давление, F – сила, S – площадь поверхности

3. A = Fs, где A – работа, F – сила, s – пройденный путь

4. U = IR, где U – напряжение, I – сила тока, R – сопротивление


Вот примеры задач, использующих эти формулы.


Задача 1. Имеются два слитка из разных сплавов, каждый массой в 720г. Плотность первого сплава на 1 г/см ³ меньше плотности второго сплава. Найдите объем каждого слитка, если известно, что объем одного из них на 10 см³ больше объема другого.


Решение задачи сводится к уравнению

720 720

х х + 10


или системе ху = 720,

(х + 10)(у – 1)=720, где х – объем , а у – плотность второго сплава.


Задача 2. На столе находится гиря массой в 200г. Когда её перевернули, площадь опоры уменьшилась на 1,5  10^-3 м², а давление на стол увеличилось на 1,2  10³ Па. Найдите площадь опоры в каждом из этих случаев.





Эта задача сводится к уравнению

2 2

х – 1,5  10^-3 х


или системе ху = 2

(х - 1,5  10^-3 )(у + 1,2  10³ ) = 2, где х – первоначальная площадь, а у – давление.


Задача 3. При перемещении тела вдоль пути АВСД на участках АВ, ВС и СД была совершена работа, равная 36 Дж, 40 Дж и 63 Дж соответственно. Из-за различного характера поверхностей этих участков сила F₂ на 2 Н меньше силы F₁ и на 1 Н больше силы F₃. найдите силы F₁,F₂,F₃, если известно, что участки АС и СД имеют одинаковую длину.





Данная задача сводится к уравнению

36 40 63

х + 2 х х – 1 , где х – величина силы F₂ .


Задача 4. К выпрямителю с напряжением 22 В подключен реостат. Когда напряжение возросло на 10%, а сопротивление реостата уменьшили на 9 Ом, сила тока в цепи увеличилась на 1,1 А. Найдите первоначальное сопротивление реостата.

Для решения этой задачи составляется уравнение

24,2 22

х – 9 х


или системе ху = 22,

(х – 9)(у + 1,1) = 24,2, где х – первоначальное сопротивление, а у – сила тока.


Хотелось бы заметить, что в курсе алгебры 8 и 9 класса для составления подобных уравнений и систем уравнений используются в основном задачи на движение, как например:

Задача 5. Чтобы ликвидировать опоздание на 1 ч, поезд на перегоне в 720 км увеличил скорость, с которой должен был идти по расписанию, на 10 км/ч.какова скорость поезда по расписанию?.

Видно, что по своему математическому содержанию задачи 1 – 4 не уступают последней, хотя их физическое содержание намного разнообразней. Интересно и то, что в задачах 1 и 5 получаются одинаковые уравнения. Совместное рассмотрение таких задач позволяет показать учителю роль математических моделей при изучении явлений различной природы. Целесообразность решения задач, использующих разнообразные сведения из физики, несомненна.


2.3. Примеры задач прикладной направленности

с различной мотивацией

• Возникновение задачи как бы «на глазах». Наблюдая за солнечным зайчиком, учащиеся замечают, что свет от одной точки до другой распространяется по прямой, выбирая кратчайший путь, равный длине отрезка между этими точками. Возникает вопрос: «По какому пути распространяется свет, если он идет от одной точки к другой не прямо, а отражаясь от поставленного на пути зеркала? Выбирает ли при этом свет наименьшее расстояние?»
  

Изучение распространения света приводит к геометрической задаче: «Точки А и В лежат в одной из полуплоскостей, образованных прямой l. На прямой lнайти такую точку, чтобы сумма расстояний от неё до двух данных точек была наименьшей».

Решение. Построим точку А₁, симметричную точке А относительно прямой l. Прямая А₁В пересекает прямую l в точке Х. длина отрезка А₁В есть кратчайшее расстояние между точками А₁ и В. Но А₁Х = АХ. Значит ломаная АХВ наименьшая, удовлетворяющая условию задачи, а точка Х– искомая.




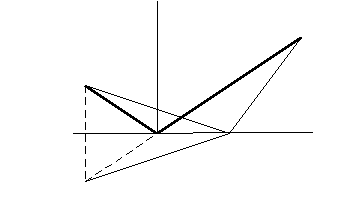
Итак, физическая задача повлекла за собой задачу геометрическую, а от неё мы совершим краткий экскурс в историю.

«Природа ничего не делает напрасно». Исходя из этого принципа, Герон Александрийский в начале нашего тысячелетия впервые высказал мысль о том, что свет распространяется кратчайшим путем, т.е. по прямой. Герон показал, что из всех ломаных линий АХВ, ведущих от предмета А к зеркалу Х и затем к глазу В, кратчайшей будет та, для которой выполняется АХХ₂ = ВХХ_1.

Так возникает ещё одна геометрическая задача:

«Доказать, что если точки А и В лежат в одной полуплоскости от прямой l и сумма расстояний от точки Х на прямой lдо точек А и В является наименьшей, то угол между лучом ХА и прямойl равен углу между лучом ХВ и прямой l.»

Решение. В предыдущей задаче точка Х была построена как точка пересечения отрезка А₁В и прямой l. Отсюда следует, что углы Х₂ХА₁ и ВХХ₁ вертикальные и АХХ₂ = ВХХ₁. Но АХХ₂ = А₁ХХ₂, так как точки А и А₁ симметричны относительно прямой l. Из доказанных равенств следует, что АХХ₂ = ВХХ_1.

Итак, физическая проблема, возникшая первоначально, помогла мотивировать появление двух типичных школьных геометрических задач. Решая их, учащиеся фактически рассмотрели геометрическую основу закона оптики, который кратко формулируется: «Угол падения равен углу отражения».

• Обращение к историческим событиям. При изучении в 11 классе темы «Площадь поверхности сферы» в современных учебниках отсутствует формула площади поверхности сферического сегмента. А нахождение такой величины может вызвать интерес, если начать урок так:
  

Сообщение ТАСС: 12 апреля 1961 года в Советском союзе выведен на орбиту вокруг Земли первый в мире космический корабль – спутник «Восток» с человеком на борту. Пилотом – космонавтом является Юрий Алексеевич Гагарин». Учащиеся, конечно, знают об этом событии. Но они могут и не знать о том, какой восторг в нашей стране и во всем мире оно вызвало. Учитель должен передать этот восторг своим чтением. «По предварительным данным, - снова начинает учитель, - период вращения корабля вокруг Земли – 89,1 мин; минимальное удаление от поверхности Земли равно 175 км, а максимальное расстояние – 302 км…». Теперь уже учащиеся удивлены: какое отношение имеет это к уроку геометрии и, в частности, к теме «Поверхность шара и его частей»? Их мысли можно прервать вопросом: «Какую часть поверхности Земли видел Ю.А.Гагарин, пребывая в апогее?».

Вопрос вызывает у учащихся интерес, но через несколько минут самостоятельных размышлений они устанавливают, что из математических знаний пока не достаточно: неизвестно, каким образом вычисляется площадь поверхности шарового сегмента. Приходится пока отложить задачу и заняться выводом формулы. Но как только формула выведена, учащиеся снова возвращаются к задаче. Её решение следует из равенств

ВО² = АО  ОК, КС = ОС – ОК = rH / ( r + H), где r = 6370 км (радиус Земли), H = АС = 302 км.

Задачу можно обогатить, предложив учащимся найти площадь поверхности Земли, которую видел Ю.А.Гагарин в течение всего полета.

Такие задачи становятся лейтмотивом урока. Решая их, выводя нужные формулы ради них, учащиеся не ждут звонка, они с неохотой отрываются от интересного исследования.

• Ссылка на первоисточники. При изучении многих тем курса математики идет ссылка в основном на математиков Древней Греции. Хотя у народов Азии математических достижений ни сколько не меньше, однако о них почему – то в большинстве учебников либо умалчивается, либо очень скудные сведения.
  

В начале 2-го тысячелетия до н.э. у народностей, населяющих территорию нынешнего Китая, образовалось классовое общество. К XVIII веку до н.э. относится возникновение рабовладельческого государства Инь. В это время уже было известно прядение и ткачество, зарождалась письменность. Одновременно развивались числовые обозначения, укоренилась десятичная система счета. В XII веке до н.э. государство Инь покорили кочевые племена Чжоу и основали новое царство, восприняв культуру завоевонного народа. Период от IV века до н.э. до VII века богат различными техническими и научными открытиями (царствование династии Цинь). В это время возникла математика и астрономия. С VII по IX века, во времена правления династии Тан, происходило дальнейшее развитие науки и техники. К X веку Китай стал обширным государством с территорией от Тихого океана до Тибета и от Великой Стены до Вьетнама.




Китай установил и расширил сотрудничество с Индией, Индонезией, Ираном и Средней Азией. В период с X по XIV века династии сменяли одна другую. В стране отмечается рост ремесел, строительство дворцов, мостов и кораблей, развитие мануфактуры и торговли. На территорию Китая проникли первые европейцы. Уровень китайской науки, достигнутый в XVI веке, стал её вершиной. Первые, дошедшие до нас, математические тексты датируются I-м тысячелетием до нашей эры. Имеются сведения о десятичной системе счисления, специальной иероглифической символике чисел, об оперировании большими числами, о наличии вспомогательных счетных устройств, о применении циркуля, линейки, угольника и т.д. китайским ученым принадлежит введение отрицательных чисел. Ко II веку до нашей эры относится создание наиболее древних из дошедших до нас сочинений – «Математика в девяти книгах», «Начала искусства вычисления», «Девять отделов искусства счета» и др.

Задача 1. Имеется два сорта чая. 3 фунта первого сорта смешаны с 6 фунтами второго, после чего фунт смеси стоит 3 дяо. Если смешать 12 фунтов первого с 4 фунтами второго, то фунт смеси будет стоить 3,5 дяо. Сколько стоит фунт первого и второго чая в отдельности?

Задача из типа на смеси, но предыстория этой задачи стимулирует учащихся на её решение.

Задача 2. Имеется амбар. Ширина 3 чжана, длина 4 чжана 5 чи; наполняющее его просо составляет 10000ху. Спрашивается, какова высота амбара? (1 чжан = 10 чи; 1 ху = 51,775 литра; 27 чжан = 10000ху)

Данная задача на применение формулы объема прямоугольного параллелепипеда.

Задача 3. Продали 2 буйвола, 5 баранов, купили 13 свиней, осталось 1000 цяней. Продали 3 буйвола, 3 свиньи, купили 9 баранов, как раз хватило. Продали 6 баранов, 8 свиней, купили 5 буйволов, не хватило 600 цяней. Сколько в отдельности стоит буйвол, баран и свинья?

Задача может быть предложена при решении систем линейных уравнений, но для более сильных учащихся, т.к. содержит три переменных.

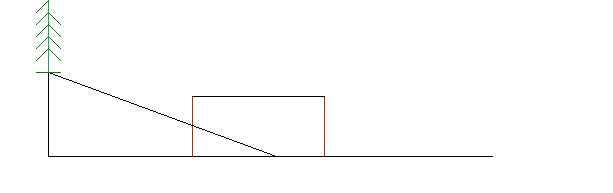
Задача 4. (из «Математического трактата о морском острове») На холме растет сосна неизвестной высоты. Внизу на равнине поставлены два шеста, каждый высотой 20 футов, на одной прямой с деревом и на расстоянии друг от друга в 50 шагов. Верхушка дерева и конец первого шеста образуют прямую с точкой на земле, расположенной в 7 шагах и 4 футах позади шеста. Верхушка дерева образует опять-таки прямую линию с концом заднего шеста и точкой на земле в 8 шагах и 5 футах позади шеста. Требуется узнать высоту сосны и расстояние от переднего шеста до холма (1 шаг = 5 футов; 1 фут = 1 чи; 1 чжан = 10 чи).

Эта геометрическая задача решается при изучении темы «Подобие треугольников»

• Народности Индии уже в глубокой древности создали богатую и разнообразную культуру, оказавшую впоследствии влияние на другие народы. Уже в период первобытно – общинного строя (XXX – XXI вв. до н.э.) индийцы сооружали оросительные каналы, были знакомы с прядением и ткачеством, применяли гончарный круг. Тогда же они строили хорошо распланированные город, в которых были системы водоснабжения и многоэтажные здания, овладели искусством, успешно развивали ювелирное дело. В течении второго тысячелетия до н.э. на территории Индии происходил процесс формирования рабовладельческих государств, закончившийся к X – VIII вв до н.э. С IV века до н.э. по VIII век индийские народности были объединены. В этот период накопились знания во всех областях культуры и науки, в том числе астрономии и математики.
  

Первые индийские математические тексты появились в эпоху составления религиозно – философских книг «Знания» («Веди»)в 1-м тысячелетии до н.э. Другие важнейшие математические рукописи появились с V по XVI век. Все они написаны на санскрите – языке индийской религии и науки. Ряд книг написан в стихах; правила, сформулированные в коротких строфах, заучивали. Математика издавна пользовалась в Индии глубоким уважением. Такое отношение к ней отчетливо выразил Брахмагупта (VII век): «Подобно тому, как солнце затмевает своим блеском звезды, так мудрец затмевает славу других людей, предлагая и особенно решая на народных собраниях математические задачи» и Бхаскара II (XII век): «Я глубоко почитаю математику, потому что знакомые с нею имеют в ней средство и понимание всего существующего; она есть основание всего видимого».