Задачи, предлагаемые при изучении некоторых тем 8 класса задачи, предлагаемые при изучении некоторых тем 9 класса
| Вид материала | Реферат |
- Т. М. Пахнова москва Работа с текстом при изучении и повторении лексики Предлагаемые, 292.07kb.
- Темы курсовых работ по дисциплине «Теория и методика обучения физике» Межпредметные, 19.14kb.
- Исследование содержания основных понятий менеджмента, 43.11kb.
- Анализ вторичного рынка Москвы июнь 2006, 18.57kb.
- Самостоятельная работа, ее роль в изучении физики. 15. Требования к оснащению учебного, 170.13kb.
- Использование национально-регионального компонента при изучении разделов и тем технологии, 144.43kb.
- Т. А. Развитие творческих способностей студентов-дефектологов при изучении дисциплин, 158.17kb.
- Учебное пособие адресовано ученикам 10 класса, изучающим курс информатики в обычных, 154.01kb.
- Учебная программа дисциплины дисциплина Старославянский язык, 455.54kb.
- Проекта, 43.2kb.
Задача 1. Известна во многих учебниках алгебры при изучении темы «Геометрическая прогрессия» «В старинной легенде рассказывается, что изобретателю шахмат предложили просить любую награду. Он попросил себе следующую: в первую клетку шахматной доски положить 1 зерно, во вторую – 2, на третью – 4 и т.д. Сколько зерен запросил мудрец себе в награду?»
Задача 2. « Два светила находятся на данном расстоянии друг от друга и движутся с разными скоростями. Когда они встретятся?»
Эта задача обошла мировую алгебраическую литературу под названием «Задача о курьерах». Заимствована она из астрономии. И вполне может быть рассмотрена при решении задач на движение.
Задача 3. (Брахмагупты) «Найди высоту свечи, зная длины теней, отбрасываемых гномоном в двух различных положениях, при условии, что известно расстояние между гномонами».
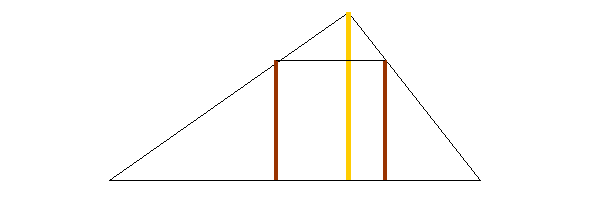
Задача 4. (Шрихарды)
Есть кадамбы цветок,
На один лепесток
Пчелок пятая часть опустилась.
Рядом тут же росла
Вся в цвету сименгда
И на ней третья часть поместилась.
Разность ты их найди,
Её трижды сложи
И тех пчел на кутай посади.
Лишь одна не нашла
Себе места нигде.
Все летала то взад, то вперед
И везде ароматом цветов наслаждалась.
Назови мне теперь,
Подсчитавши в уме,
Сколько пчелок всего здесь собралось?

Задача сводится к решению простого линейного уравнения.
х/5 + х/3 + 3 (1/3х – 1/5х) + 1 = х
- Задачи, вызывающие спор. «Два железнодорожных пути пересекаются под прямым углом. По направлению к перекрестку движутся два поезда: первый со скоростью 800м/мин, второй – 600м/мин. В 10 часов утра первый поезд находился в 40 км от перекрестка, второй в 50 км. В какой момент расстояние между поездами будет минимальным? Где будут находиться поезда в этот момент?»
Не задумываясь, многие учащиеся отвечают, что минимальное расстояние между поездами тогда, когда один из них находится на перекрестке. Но некоторые оспаривают этот ответ, утверждая, что минимальное расстояние между поездами может быть и в тот момент, когда они оба ещё не дошли до перекрестка. Для точного ответа нужно рассмотреть решение чисто математически.
Решая эту задача, учащиеся 9 класса вводят прямоугольную систему координат так, чтобы оси ОХ и ОУ совпали с направлением железнодорожных путей и предполагают, что верный ответ будет при расположении поездов как на первом рисунке.
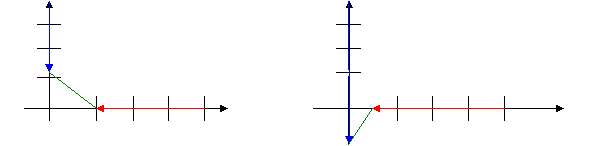
Теперь задача сводится к нахождению расстояния d между точками А1 (0; 40 – 0,8t) и В1 (50 – 0,6t; 0), где t (мин) – время движения поездов после 10 часов утра:
d = А1В1 = (50 - 0,6t)2 + (40 – 0,8t)2 = t2 - 124t + 4100 = (t – 62)2 + 256 ≥ 16.
Отсюда ясно, что dmin = 16 км при t = 62 мин. За 62 минуты первый поезд, идущий от точки А, пройдет 49,6 км, т.е. окажется за точкой О, за перекрестком. Второй поезд пройдет 37,2 км, значит он не дойдет до перекрестка 12,8 км. Таким образом, истинное расположение поездов будет таким, как на втором рисунке.
Решив задачу, учащиеся увидели, что формула для вычисления расстояния между точками вывела их из заблуждения, позволив получить и верный числовой результат и правильную схему расположения поездов, которая никак не ожидалась в самом начале.
Терпимость формулы к человеческим ошибкам, её запас прочности весьма повышает авторитет этой формулы (да и всей математики вообще) в глазах учащихся.
2.4. Пропедевтика аналитического аппарата в геометрических задачах
После изучения темы «Упрощение выражений в 6 классе можно рассмотреть с учащимися геометрические задачи, которые решаются с помощью уравнений. При этом учащиеся убедятся, что уравнения могут быть получены в результате буквенной записи соотношений между элементами фигуры.
На первом этапе обязательным сопровождением такой задачи является чертеж, предъявляемый школьникам. На чертеже указано, какая величина обозначена через х и какие обозначения получили другие величины. Приведем несколько примеров задач для решения на данном этапе.
- Составьте уравнение по рисунку и решите его. Найдите длины отрезков, обозначенных на рисунке 3х и 2х.
АВ + ВС + СД = 120 см.

1.2. Периметр треугольника на рисунке равен 288 см. найдите стороны треугольника.

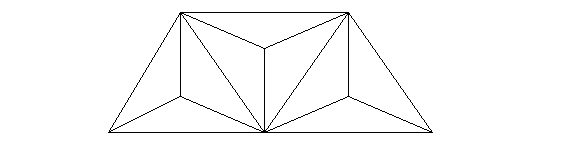
1.3. Площадь четырехугольника на рисунке равна 27 см2. Четырехугольник разбит на равные треугольники площади хсм2. Найдите площадь заштрихованной части четырехугольника.
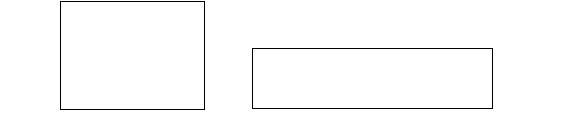
1.4. На рисунке изображены два прямоугольника, имеющие равные площади. Найдите неизвестную сторону второго прямоугольника.
1.5. Составьте уравнение по рисункам и решите их.
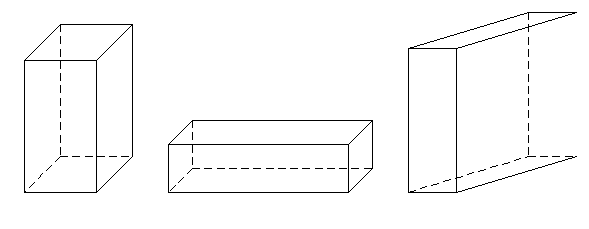
1.6. Используя рисунок, составьте уравнения и решите их, если объем прямоугольного параллелепипеда в случае а) 16дм3; б) 135дм3; в) 6м3.

Решая подобные задачи учащиеся учатся «читать» чертежи, находить в условии задачи данные для составления уравнения, обосновывать составление уравнения, интерпретировать полученные результаты. Беседа по вопросам обеспечивает активизацию учащихся. Вопросы могут быть следующие: «Какая фигура изображена на рисунке? Что известно в задаче? Что требуется найти? Как составить выражение для нахождения неизвестной величины?»
Рассмотрим теперь следующий этап – составление уравнения к текстовым задачам с геометрическим содержанием. Теперь уже ребятам самим придется сделать чертеж к задаче и на нем указать алгебраические выражения, с помощью которых будет составлено уравнение.
2.1. Отрезок АВ равен 20см. Точка С делит отрезок АВ на два отрезка, причем отрезок ВС в три раза длиннее отрезка АС. Найти длину отрезка АС. Решите с помощью уравнения..
2.2. одна из сторон прямоугольника в три раза короче другой. Найдите стороны прямоугольника, если периметр равен 192см. Решите двумя способами: с помощью уравнения и без него.
2.3. Одна из сторон прямоугольника в два раза больше другой. Найдите стороны прямоугольника, если его площадь 50см2.
При решении таких задач важно концентрировать внимание учащихся на основных моментах: введение неизвестного, обозначение других величин через неизвестное, составление выражения, описывающего соотношения между величинами, составление уравнения. Полезно разобрать различные уравнения к одной и той де задаче. Например, если в задаче 2.3. обозначить через х меньшую сторону, то уравнение получится 2х х = 50. Если же принять за х большую сторону, то уравнение примет вид 0,5х х = 50. Надо дать учащимся право самим сделать выбор и, вводя неизвестное х, составить уравнение, а затем убедиться, что при любом выборе мы получаем одинаковый результат.
На третьем этапе можно приступить к заданиям по геометрической интерпретации уравнений.
3.1. По уравнению 6х + 3х + 5х = 28 составьте задачу на: а) нахождение длин звеньев ломаной; б) длин сторон треугольника. Сделайте рисунок.
3.2. Составьте задачу на нахождение длин сторон квадрата, которая может быть решена с помощью уравнения х2 = 9. Сделайте рисунок.
3.3. Составьте задачу на нахождение длин сторон прямоугольника, которая может быть решена с помощью уравнения 3х2 = 27. Сделайте рисунок.
3.4. Составьте задачу на нахождение длин ребер куба, которую можно решить с помощью уравнения х3 = 27. Сделайте рисунок.
3.5. Дано уравнение 2,5х = 15. Составьте по этому уравнению задачу на нахождение длины одного из прямоугольников, имеющих равные площади.
Рассмотрим эту задачу подробнее. Прежде чем приступить к ней, продемонстрируем учащимся следующие заготовки (как в задаче 1.4.):
Обсудим различные возможности записи уравнения 12х = 48:
а) 2х 6 = 12 4 ; б) 3х 4 = 3 16 ; в) 4х 3 = 2 24 и т.п.
Далее переходим к задаче 3.5. Обсуждаем с учащимися различные варианты записи уравнения 2,5х = 15 и поясняем их соответствующим рисунком:
Учащиеся подводятся к тому выводу, что уравнение можно записать по-разному и для каждой записи найти соответствующие размеры прямоугольников. Ребята также убеждаются в том, что по одному и тому же уравнению можно составлять задачи с различными данными.
В более подготовленном классе работу можно усложнить, предложив учащимся самостоятельно составить задачу с совершенно другой фабулой по тому же уравнению.
Возможность различных геометрических интерпретаций одного и того же уравнения создает условия для гибкости математического мышления учащихся. Систематическое составление уравнений по рисункам геометрических фигур и, наоборот, указание геометрических интерпретаций (подчас неоднозначных) к данным аналитическим выражениям заставляет учеников мыслить в двух противоположных направлениях, что способствует формированию нешаблонного мышления.
Четвертый этап аналитической пропедевтики - составление математической модели. Рассмотрим следующие задачи:
4.1. Ученической бригаде поручили покрасить забор в детском саду. Высота забора 1м, длина 240м. В день бригада может покрасить 96 м2. Сколько дней потребуется для выполнения работы (при двусторонней покраске)?
4.2. Сколько метров ткани шириной 1,5м потребуется, чтобы изготовить покрытие для арены цирка, если диаметр арены 13м? При правильном раскрое площадь раскраиваемой ткани составляет 120% покрываемой площади.
4.3. Найдите высоту слоя песка, если для засыпки прямоугольной площадки размерами 4м и 6,9м было израсходовано 13,8 м3 песка.
4.4. Аквариум имеет форму прямоугольного параллелепипеда с размерами 1,8 1 1м. Сколько времени потребуется для заполнения аквариума водой, если в минуту в него поступает 30л?
При рассмотрении каждой из этих задач определяется форма предмета и устанавливается та величина, которая интересует нас в решении прежде всего – площадь, объем, длина и т.д.
Наиболее сложной представляется задача 4.2. Перед её решением необходимо повторить формулу площади круга и определение процента. Затем организуется беседа по вопросам: «Какую форму имеет арена цирка? Как узнать её площадь? Какую величину в задаче можно принять за 100%? Что спрашивается в задаче? Какую форму имеет отрез ткани? Какую величину удобнее принять за х?» В итоге беседы учащиеся приходят к выводу, что сравниваются площади круга и прямоугольника.
Можно сделать следующие записи:
| Площадь круга (м2) | Площадь арены с излишком в 20% (м2) | Площадь отреза ткани (м2) |
| 3,14 6,52 | 3,14 6,52 1,2 | 1,5х |
Решение задач с практическим содержанием имеет большое значение – развивает интерес к математике, показывает учащимся силу математического метода. Получая в ходе решения практической задачи её математическую модель – уравнение – и, наоборот, составляя практические задачи, для которых данное уравнение является математической моделью, учащиеся овладевают способами действий, лежащих в основе математического моделирования.
2.5. Задачи, предлагаемые при изучении
некоторых тем 8 класса.
Тема «Рациональные дроби»
- Из одного и того же пункта в одном и том же направлении отправляются Чебурашка со скоростью V1 и через t часов Крокодил Гена – со скоростью V2. Через сколько часов он догонит Чебурашку?
- У хозяйки – корзина слив. Она дала первому гостю половину всех и ещё одну, второму – половину остатка и ещё одну, третьему – половину второго остатка и ещё слив. Глядь – а корзина пустая. Сколько в ней было слив?
- Редактор стенгазеты 8 класса «Веселая перемена» поместил заметку: «Быстрее всех на школьных соревнованиях стометровку пробежал ученик нашего класса – Коля. Другие наши одноклассники пришли к финишу в таком порядке: Миша, Паша, Федя. И что удивительно – с одной той же разницей в скоростях: Коля затратил на эту дистанцию 12 сек., Миша – 13, Паша – 14, а Федя – 15». Проверьте, прав ли журналист?
Тема «Квадратный корень»
- Крокодил Гена плывет на корабле «Черепаха» со скоростью пол-узла и хочет догнать Чебурашку, который на корабле «Змей Горыныч» покрывает 100t + 100 миль за t часов. Удастся ли ему это?
- По периметру сквера, имеющего форму ромба надо посадить деревья на расстоянии 5 м друг от друга. Известно, что площадь сквера 5808 м2, а длины дорожек, идущих по диагоналям, относятся как 3 : 4. Сколько саженцев нужно для посадки?
- Арка моста имеет форму параболы у = 0,04(100 – х2) высота её 4 м, ширина основания 20 м. под ней проходит плот с грузом, упакованным в контейнер. Найти зависимость максимально возможной ширины контейнера от его высоты. Вычислите возможную ширину контейнера высотой 3м.
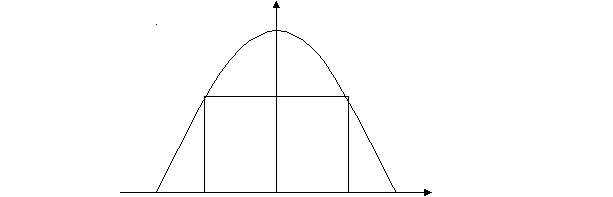
- Царь Салтан строит крепость в форме круга площадью в одну квадратную версту. И думает, какой же длины будет крепостная стена? На сколько короче эта стена по сравнению со стеной квадратной крепости с той же площадью?
Тема «Квадратные уравнения»
- На рисунке изображен проект теплицы. На её покрытие имеется 89 м2 пленки. Заданы размеры теплицы: высота 2 м, длина 5м, наклон крыши - 45º. Найдите ширину теплицы, чтобы оптимально использовать пленку.
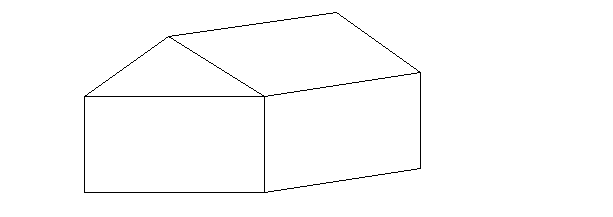
- Мальчик, стоя на склоне горы в 16м от её основания, ударил по футбольному мячу. Мяч катился вверх 3 секунды и укатился на 9м. через какое время он скатится с горки?
- У ученика 8 класса имеются резисторы с сопротивлением 2 Ома, а ему нужен резистор на 8,5 Ома. Восьмиклассник стал собирать схему их двух блоков, соединяя из последовательно: в первом блоке он соединил последовательно несколько резисторов, а во втором блоке столько же – параллельно. Получит ли он нужное сопротивление?
тема «Неравенства»
- Мама с дочкой 55 минут лепили пельмени. Пока дочь лепит 3 пельменя, мама успевает сделать не меньше 4 штук, но через каждые 15 минут она отвлекается на 5 минут, чтобы раскатать тесто. Кто слепил больше пельменей?
- Бублик имеет дырку радиусом 5 см, а радиус внешнего края – 7 см. Оцените объем бублика.
- Из куска проволоки диной 20 см требуется изготовить модель треугольника со сторонами 7 и 9 см. какой может быть третья сторона?
тема «Степень с целым показателем»
- Среднее расстояние от Солнца до планет солнечной системы равно:
- Меркурий 58 млн.км
- Венера 108 млн.км
- Земля 150 млн.км
- Марс 228 млн.км
- Юпитер 778 млн.км
- Сатурн 1430 млн.км
- Уран 2870 млн.км
- Нептун 4500 млн.км
- Плутон 5900 млн.км
- Меркурий 58 млн.км
Выразить это расстояние в световых годах (1 св.год = 9,461012 км)

- Окись углерода вредна для здоровья, в жилых помещениях её содержание не должно превышать 0,2 10-2 г/м3. Какое максимально допустимое число молекул может находиться в помещении размером 4 5 2,5 м?
- В тридевятом царстве живет дракон, который увеличивает свой вес за день в 4 раза, если поймает и съест добра молодца; вдвое, если – красну девицу, и худеет на половину своего веса, если останется без добычи. За год он съел 15 девиц и 112 молодцев. Как изменился его вес за это время?
2.6. Задачи, предлагаемые при изучении
некоторых тем 9 класса.
тема «Квадратичная функция»
- Требуется изготовить ковш в форме усеченного конуса объемом 3л, высотой 20см, с диаметром нижнего основания 10см. Каков диаметр верхнего основания?
справка: объем прямого усеченного конуса равен
V = h/12 (d12 + d1d2 + d22),
где h – высота, d1 ,d2 – диаметры оснований
- Агрономическими опытами установлена следующая зависимость между среднесуточной температурой Т, при которой выращивалась пшеница, и её урожаем У:
-
Т (ºС)
14
16
22
У (кг/м2)
0,91
1,06
0,88
Найдите квадратичную зависимость у = аТ2 + вТ + с между урожайностью и температурой. По этой зависимости найти оптимальную температуру, которая обеспечивает максимальный урожай.
- После начала торможения движение электропоезда описывается законом S = 16t – 0,1t2, а скорость меняется по закону V = 16 – 0,2t, где t – время (с), V – скорость (м/с), S – пройденный путь (м). через сколько секунд поезд остановится? Каков его тормозной путь? Составьте таблицу изменения скорости и пройденного пути за это время (с интервалом 10 сек) и нанесите на графики S = S(t) и V = V(t).
Тема «Неравенства»
- Из автомата выстрелили вертикально вверх, пуля полетела с начальной скоростью 500 м/с. Пренебрегая сопротивлением воздуха, найдите, через какое время после выстрела пуля будет находиться выше 4,5м.
- Разбивается парк. Частью его является прямоугольная лужайка с площадью не менее 1 га, а одна из сторон прямоугольника на 45см больше другой. Вокруг лужайки строится дорожка шириной 4м. сколько для нее потребуется гравия, если его насыпать слоем не менее 15см?
Тема «Целые уравнения»
- Среднее геометрическое двух положительных чисел обычно меньше среднего арифметического. Например, для чисел а = 9, в = 25 (а + в)/2 = 17, ав = 15, т.е. ав (а + в)/2. Докажите это неравенство. Найдите, в каком случае оно превращается в равенство. Когда среднее геометрическое составляет 60% от среднего арифметического?
- В кружке технического творчества устроили соревнование роботов на дистанции 600м. первый робот прошел 200м с некоторой начальной скоростью V, затем 378м – со скоростью на 2м/мин большей и остановился – кончился ресурс батарей. Второго робота сразу запустили со скоростью (V + 1) м/мин, а через 540м скорость увеличили ещё на 2м/мин. Через 56м остановился и второй робот, пройдя на 3мин больше первого. Так как они не преодолели дистанцию, победу присудили первому роботу, который прошел дистанцию с большей скоростью. Найдите его начальную скорость.
Тема «Системы уравнений»
- Уравнение орбиты Земли у2 = 0,9997 (1 – (х - 0,017)2), а уравнение траектории кометы Галлея у2 = 0,06466 (322,2 – (х – 17,36)2). Может ли Земля столкнуться с кометой Галлея?
Чтобы найти точки пересечения траекторий этих двух небесных тел, надо решить систему уравнений
у2 = 0,9997 (1 – (х - 0,017)2),
у2 = 0,06466 (322,2 – (х – 17,36)2).
Левые части уравнений равны. Приравнивая правые, раскрывая скобки и приводя подобные слагаемые, получим
0,9353х2 – 2,211х + 0,3493 = 0,
х2 – 2,364х + 0,3734 = 0.
Чтобы ответить на вопрос задачи, достаточно найти дискриминант
Д/4 = 1,1822 – 0,3734 0,
Следовательно, уравнение имеет корни, и есть вероятность столкновения Земли с кометой Галлея.
- Незнайка заказал Винтику и Шпунтику шкаф.
- Чтобы одна сторона была 210, другая – 280, а третья – 300
- Чего? Сантиметров?
- Нет. Дециметров
- Как это?
- Квадратных
Найдите размеры шкафа.
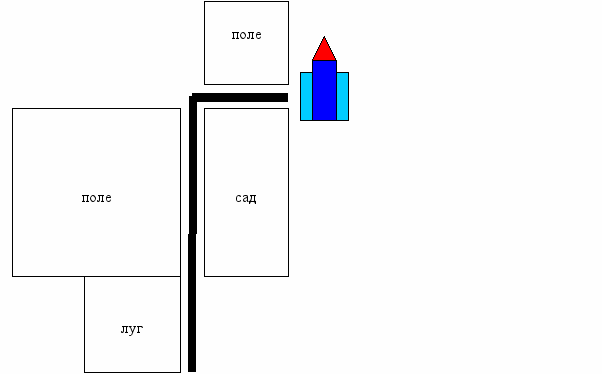
- - Эй, чей это луг вы косите?
- Маркиза Карабаса! – в один голос отвечали косцы.
Помните, что дальше было в сказке «Кот в сапогах»?
- А кому принадлежат эти поля?
- Маркизу Карабасу.
Дальше был сад, мельница и, наконец, замок. Его величество не мог, конечно, не оценить прекрасных владений маркиза и поинтересовался их размерами.
Так вот, дорога, по которой ехали король, принцесса и марких, была длиной 2 лье, т.е. 9км. Угодья слева от дороги (луг и поле) – 2900га, а сад – 800га. Найдите размеры всех угодий.
тема «Последовательности»
- На Поле чудес растут волшебные деревья с золотыми монетами. Каждую ночь на каждом дереве вырастает одна монета.1 мая на них висело 1000 монет. В мае Буратино посадил еще одно дерево. 31 мая на деревьях стало 1995 монет. В какой день Буратино посадил дерево? Какую последовательность образует количество монет на деревьях каждый день мая?
- Каждая ступенька пирамиды имеет форму параллелепипеда с квадратом в основании и одну и ту же высоту - 0,8м. Сторона основания пирамиды-50 м, а у каждой следующей ступени она уменьшается на 2 м. Сколько ступеней у пирамиды, какова сторона основания последней? Каковы высота и объем пирамиды?
- Сосчитайте, сколько мух появилось бы за полгода от одной пары, если бы их потомство не погибало, а полностью сохранялось. Муха откладывает 160 яиц, будем считать, что в новом поколении половина само, они становятся взрослыми через 20 дней и откладывают яйца только один раз. Чтобы представить себе количество мух через 6 месяцев, оцените, как они будут распределены по всей суше (площадь суши на земле – 1, 5 108 км2 = 1,5 1014 м2)
- Банк начисляет вкладчику за год долю х от вклада ( т.е 100 х %). Какая сумма будет на счету через t лет, если первоначальный вклад был Р руб.?

Тема «Степень с рациональным показателем»
- Периоды обращения планет вокруг Солнца приведены в таблице (в земных годах):
Меркурий 0,24
Венера 0,62
Земля 1
Марс 1,9
Юпитер 12
Сатурн 29,5
Уран 84
Нептун 165
Плутон 248
Вычислите средние расстояния от Солнца до этих планет (в астрономических единицах). Справка: если известны периоды обращения планет и расстояние R1 от Солнца до одной из планет, то другие расстояния можно найти по закону Кеплера:
R2 = R1 (T2/T1)3/2 .
Среднее расстояние от Солнца до Земли равно 1 а.е. = 149597892 км.
- Хозяйка сварила суп и кашу. Чтобы кастрюля с кашей не остыла
слишком быстро, она завернула её в одеяло, а суп оставила на
плите. Через час температура каши понизилась до 60º, а супа – до
30º. При этом температура воздуха в комнате была 20º. Какова
будет температура супа и каши через 2 часа? Составьте таблицу
зависимости их температур от времени (0 t 60мин) с шагом 5
мин. И нанесите обе кривые на один график.
Справка: температура тела изменяется по закону Ньютона Т = (То – Тс)/2кt + Тс, где То = 100º - начальная температура тел, Тс = 20º - температура среды. Значения коэффициента k найти из условия, что температуры через t = 60мин известны.
- Скорость резания, допустимая при обтачивании стали на токарном станке, вычисляется по формуле V = 580 Т-1/3 Н-1/5 а-2/5 (м/мин), где Т(мин) – стойкость резца (время непрерывной работы до затупления), Н (мм) – глубина резания, а (мм/об) – скорость подачи. Вычислите V при следующих значениях параметров: Т=60 мин, Н = 3мм, а = 0,2 мм/об.
Тема «Тригонометрия»
- Есть много способов измерения недоступных расстояний путем решения треугольников. Вот один из способов определения высоты скал, зданий, к которым нельзя подойти (недоступно основание высоты). Измеряют базис а и углы , . Как найти Н?
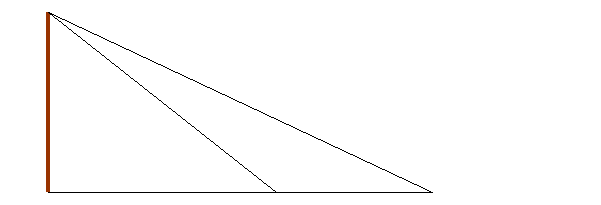
а = АС – ВС = Нctg - Hctg = H (ctg - ctg),
Н = а / (ctg - ctg)
- Кастрюля диаметром 26см и высотой 15см наполнена водой. Под каким минимальным углом к горизонту надо посмотреть, чтобы увидеть центр её дна? Какова будет при этом «кажущаяся глубина» кастрюли – больше или меньше реальной глубины?





Чтобы увидеть центр дна, угол отражения должен быть равен ВСО. Найдем соответствующие ему углы , :
sin = ОВ/ОС = 0,655
sin = 1,33 0,65 = 0,871, = 60º35, где 1,33 – показатель преломления двух сред для воды.
Угол к горизонту = 29º25. «Кажущаяся глубина» будет равна отрезку О1Д (точку О мы видим на месте О1), т.е. h1 = О1Д = СД ctg = 13 0,563 = 7,3см h/2.
Приведем еще несколько примеров задач.
- Три латунных куба с ребрами 3, 4, и 5 дм переплавили в один куб. Найти длину ребра получившегося куба.
- Чугунная труба имеет квадратное сечение, её внешняя ширина 25 см, толщина стен 3см. какова масса одного погонного метра трубы?
- Какое количество нефти (в тоннах) вмещает цистерна, имеющая форму цилиндра, с диаметром 18 м и высотой 7 м. (В данных задачах возникает необходимость взять из справочного материала плотность чугуна и нефти)
- Бревно длиной 20 дм имеет форму усеченного конуса с диаметрами 2 дм и 1 дм. Необходимо вырубить брус с квадратным сечением максимального объема, ось которого совпадает с осью бревна.
- Диаметр Луны составляет ¼ диаметра Земли. Сравните их объемы.
- Сколько кубических метров земли потребуется для клумбы в форме шарового сегмента с радиусом основания 5 м и высотой 60 см.
- Стаканчик мороженого имеет форму конуса высотой 12 см и диаметром 5 см. в стаканчик положили две ложки мороженого в форме полушарий диаметра 4 см. переполнит ли мороженое стаканчик?
Заключение
Цели прикладной направленности обучения математике: формирование конкретных представлений о роли и месте математики в жизни современного общества и формирование знаний, умений и навыков, необходимых для решения практических задач с помощью математики.
Главное в работе учителя по усилению прикладной направленности обучения – постоянная ориентация на применение изучаемого и системный подход к этой проблеме, заключающийся в следующем:
- Усиление прикладной направленности при изучении основных содержательных линий. При этом задача учителя состоит в том, чтобы наполнить абстрактные понятия жизненным содержанием, убедить учащихся в необходимости математического метода познания и показать, что математические знания нужны не только тем, кто посвятит себя научной деятельности, но и тем, кто станет заниматься практическими делами.
- Реализация прикладной направленности обучения с учетом структуры и логики построения учебного материала (осуществление внутрипредметных связей при изучении основных содержательных линий)
- Осуществление двухсторонних межпредметных связей. У значительной части учащихся интерес к математике проходит именно через знакомство с её приложениями, когда они видят реальную пользу абстрактных теорий.
- Использование внеклассной работы для усиления прикладной направленности обучения математике, основными направлениями которой являются:
- Развитие представлений о широте применимости и роли математики в науке, технике и производстве
- Углубление математических знаний (изучение внепрограммного материала прикладного характера)
- Формирование умений применять математические знания в практической деятельности
- Развитие прикладных умений и навыков
- Развитие представлений о широте применимости и роли математики в науке, технике и производстве
Возможностей для этого много: факультативы, кружковая работа, вечера, конференции, викторины, конкурсы, ученические рефераты, оформление кабинета математики.
Список использованной литературы
- А.А.Темербекова. Методика преподавания математики. Учебник для ВУЗов. 2003г.
- В.П.Краснощекова. Прикладная направленность обучения математики в средней школе. Методические разработки по спецкурсу. Пермь, 1997г.
- Ю.М.Колягин. Задачи в обучении математике. М.:Просвещение.1997г.
- Н.А.Терешин. Прикладная направленность школьного курса математики: Кн. Для учителя. М.: Просвещение. 1990г.
- И.М.Шапиро. Использование задач с практическим содержанием в преподавании математики. М.: Просвещение, 1990г.
- А.Е.Малых. История математики в задачах. ПОИПКРО, Пермь 1994г.
- М.А.Фоминых, Ю.Ф.Фоминых. Алгебра – 8. Прикладные задачи. Пермь, 1993г.
- М.А.Фоминых, Ю.Ф.Фоминых. Алгебра – 9. Прикладные задачи. Пермь, 1993г.
- «Математика в школе». Научно – методический журнал. №2, 1981г.; №5, 6, 1985г.; №2,3,1987г.; №2, 1988г.; №2, 1990г.; №3, 1991г.
- Математика. Приложение к газете «Первое сентября», «№ 11, 12, 2004г.
- Региональные стандарты математического образования для города Перми. Пермь, 1995г.
ПРИЛОЖЕНИЯ
Результаты районного мониторинга по математики
в 2003 - 2004 учебном году
В 2003 – 2004 учебном году в МОУ «СОШ № 55» был проведен районный мониторинг, во время которого один из этапов назывался «Прикладная направленность математики». В мониторинге участвовали все учащиеся 5 – 11 классов.
Проанализировав результаты выполнения данных работ в классах, в которых я работала (9 «Д» и 5 «Б»), получились следующие результаты:
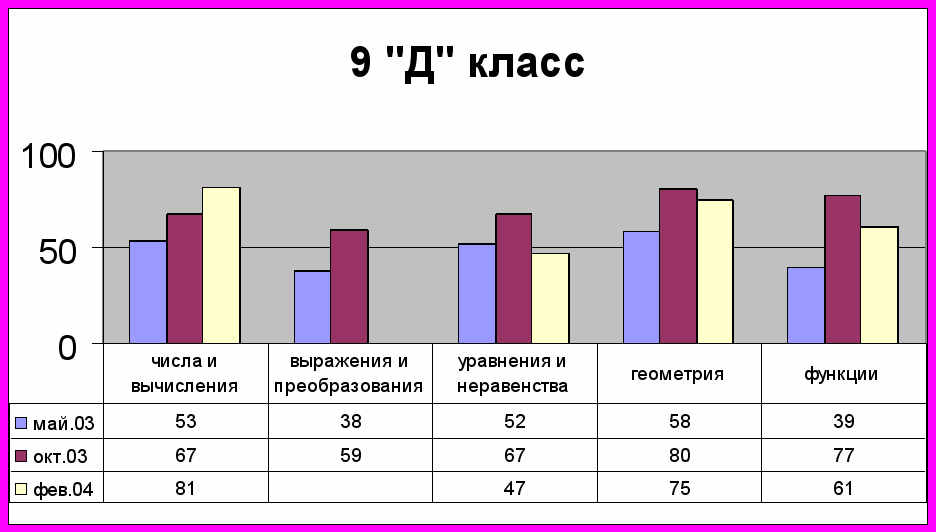
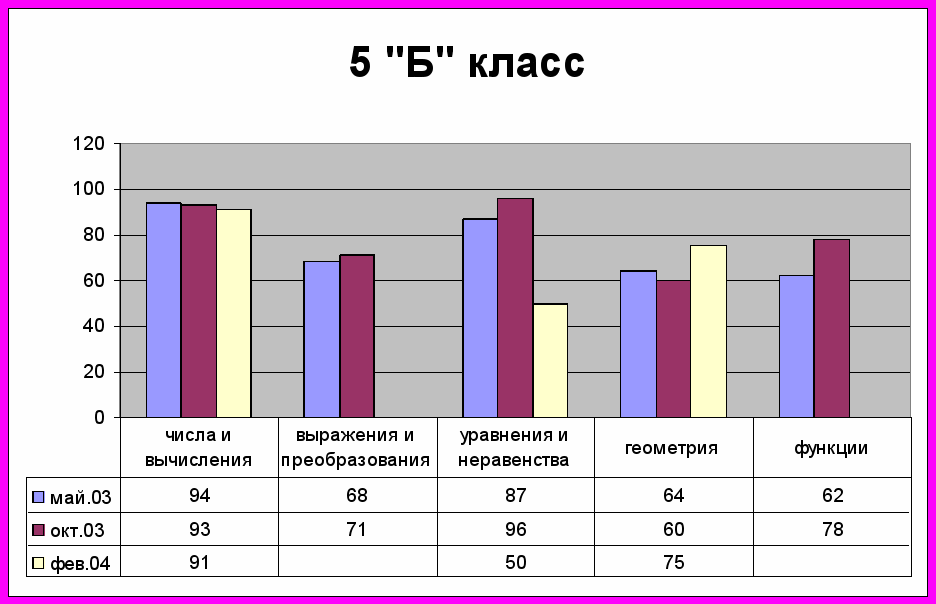
В обоих классах к началу нового учебного 2003 – 2004 года показатель успеваемости по всем содержательным линиям находится на довольно высоком уровне (октябрь 2003 года). При написании теста с тематикой «Прикладная направленность математики» (февраль 2004) результаты в целом хорошие. В большинстве содержательных линий процент успеваемости намного выше отметки 50 %. Падение в целом успеваемости при написании данного теста можно объяснить лишь спецификой заданий прикладного характера.
Причем очень высокий уровень написания прикладного теста учащимися 5 «Б» класса объясняется тем, что учащиеся идут по программе «Школа 2100», в которой достаточно много места и времени уже в рамках программы отдается заданиям прикладного характера, навыкам логического мышления. Учащиеся без труда решают задания, не требующие специальных математических умений и навыков, а лишь необходимо применить математические методы решения тех или иных заданий.
Конспект урока в 8 классе
«Вписанный угол и его величина»
Данный урок является пятым из семи уроков, отведенных на изучение темы «Окружность». На одном из первых уроков ученицей класса была проведена беседа, знакомящая учащихся с историей возникновения термина «окружность» и её основных элементов.
Окружность – самая простая из кривых линий. Это одна из древнейших геометрических фигур. Философы древности придавали ей большое значение. Согласно Аристотелю, небесная материя, из которой состоят планеты и звезды, как самая совершенная должна двигаться по самой совершенной линии – окружности. Сотни лет астрономы считали, что планеты двигаются по окружности. Это ошибочное мнение было опровергнуто лишь в XVII веке учениями Коперника, Галилея, Кеплера и Ньютона.
Ещё вавилоняне и древние индийцы считали самым важным элементом окружности – радиус. Слово это латинское и означает «луч». В древности не было этого термина. Евклид и другие ученые говорили просто «прямая из центра». В одной латинской рукописи XIв., названной «Искусство геометрии» и приписывается римскому автору Боэцию, встречается впервые термин «полудиаметр». Его употребляли также Фибоначчи и Неморарий (XIIIв.), Региомонтан (XVв.) и Тарталья (XVIв).
Термин «радиус» впервые встречается в «Геометрии» французского ученого Рамуса, изданной в 1568г., а затем у Франсуа Виета. Последний писал, что «радиус» - это «элегантное слово», которое римские поэты Овидий и Виргилий употребляли в смысле «луч». Известный римский оратор Цицерон как-то сказал: «Шар образован равными радиусами (лучами), выходящими из его центра». Термин «радиус» становится общепринятым лишь в конце XVIIв. Термин «хорда» (от греческого «хорде» - струна) был введен в современном смысле европейскими учеными XII – XIIIвв.
Определение касательной, как прямой, имеющей с окружностью только одну общую точку, встречается впервые в учебнике «Элементы геометрии французского математика Лежандра (1752 – 1833). В «Началах» Евклида дается следующее определение: прямая касается круга, если она встречает круг, но при продолжении его не пересекает.
То, что касательная к окружности перпендикулярна к радиусу, проведенному в точку касания, было известно ещё Архиту Тарентскому (430 – 365 гг. до н.э.)
Архит – один из талантливейших греческих математиков – пифагорейцев, астроном и государственный деятель. В настоящее время некоторые историки считают его автором VII книги «Начал» Евклида. Древнеримский архитектор Витрувий (Iв.) рассказывает, что Архит был также замечательным инженером – механиком, строил разные машины, в том числе летающего деревянного голубя, детскую трещотку и др. В трудах Архита тесно переплетаются теория чисел, геометрия, теория музыки. Идеи Архита оказали большое влияние на Платона и на дальнейшее развитие греческой математики.
Доказательство того, что отрезки касательных, проведенных из одной точки к окружности, равны, отсутствует у Евклида и приписывается Герону Александрийскому.
К данному уроку учащиеся знакомы с понятиями касательной и её свойств, центрального угла и его величины. Урок начинается с отгадывания кроссворда, который висит на доске:
-
10
11
2
6
4
7
1
13
12
9
5
3
8
- Самая совершенная линия по мнению Аристотеля
- Элегантное слово, которое римские поэты Овидий и Верилий употребляли в смысле «луч»
- В переводе с греческого – «струна»
- Хорда, проходящая через центр окружности
- Часть окружности
- Единица измерения углов и дуг
- Угол с вершиной в центре окружности
- Прямая, которая встречает круг, но при продолжении не пересекает его (Евклид)
- Прямая, имеющая с окружностью две точки
- Идеальный параллелограмм, в котором легко вписывается окружность
- Математик, организовавший в Сицилии свою школу
- Угол между касательной и радиусом, проведенным в точку касания
- Род искусства, которым помимо геометрии занимался древнегреческий математик Архит
После отгадывания кроссворда, по вертикали образуется слово «вписанный» - это и будет тема сегодняшнего урока, вводится определение вписанного угла.
На доске рисунок:
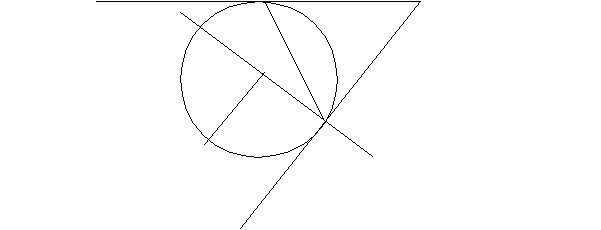
Найти на рисунке понятия и их свойства: окружность, радиус, диаметр, хорда, касательная, секущая, дуга, центральный угол, вписанный угол.
Используя эти факты, самостоятельная работа по рядам (можно совещаться) с последующим обсуждением у доски:

ВС = радиусу АВ:ВС:АС=1:2:3 АД = 70º, ВС=50º
Найти:АВС Найти:АВ, ВС, АС АО = 15
АОС Найти:ДС, ДОВ.
Далее доказывается теорема о величине вписанного угла с рассмотрением первых двух случаев, третий случай дается в домашнюю работу.
После доказательства запись двух следствий:
- вписанные углы, опирающиеся на одну и ту же дугу, равны
- вписанный угол, опирающийся на диаметр – прямой
Потом решение трех устных задач на применение величины вписанного угла и его свойств:
- Какой угол охватывает глаз лошади, когда она находится на краю арены, если она видит 1/6 часть окружности?
- Под каким углом баскетболист видит сторону площадки с кольцом, находясь на трехочковой линии?
- Какой величины надо отрезать дуги от дольки апельсина для украшения торта, если нужно вырезать равносторонний треугольник?
В оставшуюся часть урока решение заданий из учебника.
Конспект урока математики в 5 классе
«Восхождение на Олимп
или
ещё раз об обыкновенных дробях»
Весь урок построен по типу «путешествия». На своем пути учащиеся встречаются с математиками Древней Греции, которые предлагают им различные задания. К данному уроку учащиеся знакомы со всеми действиями с дробями и умеют решать задачи трех типов на части: нахождение части от целого, целого по его части и какую часть составляет одно от другого.
На доске задача, написанная в форме папируса
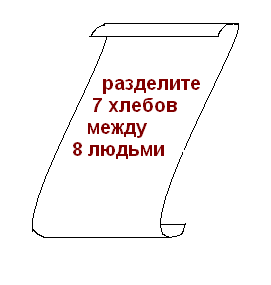
Учащимся предлагается, посмотрев на задачу, назвать тему и цель урока.
Совместными усилиями выясняется, тема - «Обыкновенные дроби», цель – повторение и закрепление ранее изученного.
Наш сегодняшний урок – один из последних в этой теме. С дробями люди познакомились очень давно, а т.к. самые знаменитые математики были греками, мы с вами отправляемся в Древнюю Грецию, где встретимся с некоторыми математиками. Вспомните, пожалуйста, самое высокое место в Древней Греции – ОЛИМП. И мы отправляемся на «Математический Олимп». Путь наш не короткий, но и не длинный, потому что об обыкновенных дробях вы знаете достаточно много, но ещё и не все; не простой, но и не очень сложный, потому что многие из вас без труда решает сложные задачи.
Доска открывается и на ней портреты математиков: Пифагора, Евклида, Фалеса и Архимеда.
- Итак, первый на нашем пути Пифагор – один из самых известных математиков, родился на острове Самос и знаменит тем, что открыл Пифагорийскую школу, в которой занимались не только математикой, но и другими науками, в частности философией. Одно высказывание мне хотелось бы вам привести: «Сыщи себе верного друга; имея его ты можешь обойтись без богов». Как вы это понимаете?
Пифагор первым разделил числа на четные и нечетные, простые и составные. Пифагор предлагает вам отгадать его кроссворд, заодно и вспомним некоторые правила действий с дробями.
-
2
5
1
4
3
1. Число, показывающее, на сколько равных частей разделено целое
- Дробная черта – это действие …
- Деление числителя и знаменателя на одно и тоже число называется …
- Определите, не прибегая к вычислениям, какое выражение больше (первое или второе): 1 – 1/2003 или 1 – 1/2004?
- Плод банан состоит из кожуры и мякоти. Кожура составляет 2/5 массы банана. Если бананы весят 10 кг, то сколько весит мякоть?
А сколько стихов было написано в Пифагорийской школе. Я начинаю, а вы мне в рифму отвечайте:
Каждый может за версту
Видеть дробную черту.
Над чертой – числитель, знайте,
Под чертою – знаменатель.
Дробь такую непременно
Надо звать обыкновенной.
Посмотрите, что за дробь –
Дробь обыкновенная.
Проведем сегодня с ней
Действия мгновенные
Одна вторая плюс две пятых
Сколько будет? …
Действие неверное –
Действие мгновенное.
Ну а правильный ответ
Кто мне даст?
Чтобы дроби вычесть или сложить
Надо общий знаменатель получить
Дробь на дробь просто умножить
Надо числители и знаменатели перемножить
Несложно дроби и разделить:
Стоит лишь вторую заменить
Дробью для нас приятной,
Называется – обратной.
Мы с вами повторили все правила действий с дробями, продолжаем путь дальше.
- Следующий на нашем пути – Евклид, родившийся в г.Александрия, которая знакома вам по знаменитому Александрийскому маяку – одному из семи чудес света. Евклид является автором первого учебника по геометрии. Одна из легенд рассказывает, что к Евклиду обратился юноша с просьбой взять его в ученики, сказав, что желает изучать геометрию, она ему несомненно нужна. Вместо ответа Евклид повелел своему слуге:»Дай этому человеку три обола (древняя монета), он ищет в геометрии пользу».
Евклид предлагает вам решить несколько задач (по вариантам)
- Чтобы построить дом, богатому греку нужно нанять 36 рабочих. 4/9 из них должны быть плотники, 1/6 – каменщики, остальные – разнорабочие. Сколько разнорабочих занято на строительстве?
- На своем участке земледелец посадил 3 локтя пшеницы и 5 локтей гречи, что составило 4/21 от всей площади земельного участка. Какова площадь участка?
- Фалес. Этот математик родился в г.Милет и также как Пифагор знаменит своей школой. Известно, что Евклид при написании своей книги пользовался очень многими открытиями Фалеса.
Говорят, что Фалес первым посоветовал морякам ориентироваться по Полярной звезде. Давайте и мы с вами посмотри на «наше» небо.
Учитель лазером рисует на потолке разные цифры – для учащихся это разминка для глаз.
А Фалес предлагает вам посчитать.
Предлагаются цепочки вычислений, задания к которым разложены на партах заранее. Смысл задания:
У каждого ученика карточка с порядковым номером и заданием, которое необходимо выполнить с ответом предыдущего участника. У первого номера пример целиком. Весь класс разбит на три группы (по рядам). Ответы выписываются на доске. Каждый ученик будет выходить для этого к доске – хорошая физическая разминка.
- Последний математик, встретившийся на нашем пути – Архимед. Он родился в г.Сиракузы. этот великий ученый подарил человечеству крылатое восклицание: «ЭВРИКА!»
И я вам предлагаю сделать небольшое открытие. Одним из самых загадочных образов математики является магический квадрат, его «волшебность» заключается в том, что по всем вертикалям, горизонталям и диагоналям сумма чисел одинаковая. Я вам предлагаю его заполнить. Одно число я уже записала, три вы впишите, решив задачи, а остальные посчитаете.
-
1.
3.
2.
1
2
- Чтобы слепить статую богини скульптору нужно 50 кг различного материала – 24 кг глины, 16 кг гипса, остальное – вода. Какую часть всех материалов составляет вода?
- Греческая аристократка приобрела на рынке 5 метров льна для пошива платья, 3/25 этого количества она отдаст швеям за работу. Сколько материала получают швеи?
- На изготовление глиняного горшка у ремесленника ушло 1/10 пуда глины, что составляет 1/7 от всех имеющихся у него запасов. Сколько центнеров глины у ремесленника в запасе?
Нужно вписать ответы в соответствующие клетки квадрата и заполнить его до конца.
Итак, мы с вами преодолели не простой путь и взобрались на вершину горы, которую образно в начале урока назвали «Математический Олимп».
Давайте определим, все ли успешно совершили восхождение. Кто считает, что его вершина достигнута и нечего больше делать?
Современную систему записи дробей с числителями и знаменателями создали в Индии, только там писали наоборот – числитель внизу, а знаменатель – наверху. Записывать дроби в точности, как сейчас, стали арабы, но с ними мы встретимся в следующий раз.
Урок математики в 6 классе
«Немного из истории Перми»
(задачи с процентами)
За столом учителя сидят два человека за компьютером – контролеры (учителя математики).
Парты в классе стоят в два ряда по 6 парт
Учитель: мы с вами совершим путешествие по Перми, я буду вашим экскурсоводом, мне помогают мои коллеги - учителя, которые будет фиксировать все ваши ответы и которые в конце путешествия сообщат об итогах.
Для того, чтобы начать путешествие, давайте определимся, о чем мы будем говорить и что хотим получить в итоге: изучаемая тема – проценты, задачи на проценты; я уже сказала, что мы отправляемся в небольшую экскурсию по городу Перми. Значит сегодня на уроке мы будем выполнять задания с процентами, в которых речь будет идти о нашем городе. Закрепим свои знания о процентах, узнаем нечто новое т городе Перми.
