Фельдман А. Б. Производные финансовые и товарные инструменты

Вид материала

Документы

Содержание Фьючерс на индекс курсов акций. Таблица 12.1 Арбитраж при надежных выплатах дивидендов Фьючерсы с базисом в виде обменного курса валют. Фьючерсы, основанные на облигациях. О "базисе" в технологиях фьючерсов.

Подобный материал:

• Программа дисциплины Производные финансовые инструменты для направления 080105., 107.25kb.
• Программа дисциплины Производные финансовые инструменты и реальные опционы для направления, 423.51kb.
• Лекции по курсу «Производные финансовые инструменты», 258.65kb.
• Лекции по курсу «Производные финансовые инструменты», 158.65kb.
• Лекции по курсу «Производные финансовые инструменты», 358.4kb.
• Лекции по курсу «Производные финансовые инструменты», 239.66kb.
• Производные финансовые инструменты посещаемость: сентябрь – октябрь 201 1 года, 394.53kb.
• Лекции Селищева А. С. «Производные финансовые инструменты», 171.47kb.
• Лекционый курс: «Производные финансовые инструменты» Содержание: Часть I. Деривативы, 1515.17kb.
• Вопрос 6 раздел 2 Инвестирование в финансовые инструменты, 95.53kb.

Здесь и далее в приложении под символом r_f понимается (1 + i), где i – соответственно безрисковая процентная ставка.

Фьючерс на индекс курсов акций. Условимся, что в течение срока действия фьючерса выплаты дивидендов по акциям, учтенным в данном индексе, будут надежными, предсказуемыми. Участник рынка может выбирать между покупкой портфеля акций и соответствующих фьючерсов. Реализация арбитража при периодически выплачиваемых дивидендах применительно к фьючерсам на индексы демонстрируется в табл. 12.1.


Таблица 12.1

Арбитраж при надежных выплатах дивидендов

Действие	Платежные потоки
	в момент t0	в момент T
Покупка портфеля акций, составляющих индекс	–S	S(T) + n Σ  Dj rT–tj j=1
Продажа фьючерса	0	F–S(T)
Денежный вклад (займ)	+S	–SrfT
Результат	0	F – SrfT + n Σ   Dj rT–tj j=1

Примечание. В таблице принято: t_j – момент выплаты дивидендов по каждой i-й акции.

При нарушении равновесия (равенства) у инвестора появляются арбитражные (спекулятивные) возможности. Если рыночная цена фьючерса на индекс акций превысит теоретическую цену (цену равновесия), то участник рынка займет позицию длинного арбитража, в соответствии с которой в текущий момент он продает подорожавший фьючерс, покупает индексный портфель акций, принимая денежный займ по безрисковой процентной ставке. Станет цена фьючерса ниже теоретической цены, тогда участник рынка может занять позицию короткого арбитража и провести сделки, прямо противоположные предыдущей ситуации.


На рынке наряду с обычными индексами курсов акций применяется индекс исполнения (Performance Index). Стоимость фьючерса на такой индекс предполагает обнуление дивиденда, и формула справедливой цены при годовой процентной ставке: F = S(1 + i)^T = Sr_f^T [см. формулу (12.1)].

В 1992 г. была предложена запись этого выражения (для индекса DAX)¹:


F = S(1+i)

Число дней до исполнения

360

Фьючерсы с базисом в виде обменного курса валют. В основе определения стоимости этого фьючерса (как показано и в главе 8) лежит суждение, что цена фьючерса должна отвечать такому соотношению между вкладом в национальной валюте при действующей процентной ставке и соразмерным (с обменным курсом) прямым вкладом в иностранной валюте с процентной ставкой на внутреннем рынке чужой валюты, при котором достигалось бы равенство доходов партнеров в данных валютах (или ситуация паритета процентных ставок – Interest Rate Parity). Тогда²:

F = S	(1+ia)T
	(1+ii)T

Фьючерсы, основанные на облигациях. Для их оценки признанной стала модель Но – Lee³.

Модель Но – Lee выявляет, основываясь на текущей ситуации с процентами, их будущее развитие. Для этого текущая структура процентов (совокупность их величин) рассматривается либо как функция процентных ставок в их связи со временем, либо как функция курса облигаций с нулевым купоном (Zero-Coupon). В последующем рассматривается только вторая версия.

В модели Но – Lee предполагается, что рынок капиталов свободен от внутренних распрей, отсутствуют выплаты налогов и платежи посредникам, облигации могут продаваться и покупаться в любом делимом количестве, а для каждого наблюдаемого момента времени существует необходимый облигационный займ с нулевым купоном. При этом также предполагается, что число рыночных ситуаций ограничено, а рыночные ожидания связаны с дискретными периодами времени.

В модели для выхода на достоверные решения по фьючерсам, основанным на процентах, принят также ряд требований: расчеты должны быть свободными от арбитража и основываться на описании динамики курсов многих купонных облигаций; модель движения структуры процентов должна соответствовать текущим показателям структуры процентов; должна быть обеспечена легкость при определении параметров модели.

Решение основано на использовании биномиальной модели (см. опционы). Предложен вывод: цена фьючерса в момент t₀ равна ожидаемому кассовому курсу базиса в момент исполнения фьючерса при вероятности q, нейтральной к риску. Это суждение выражается формулами

F₀ = Ê₀

и

Ê₀ = NWP_T1(T2),

где F₀ – цена фьючерса в момент t₀;

Ê₀ – ожидаемая стоимость базиса в момент t₀ при вероятности q, нейтральной к риску;

NW – принятая процентная ставка, по номиналу;

T₁– момент исполнения фьючерса;

T₂ – момент исполнения базиса;

P_T1(T2)– цена облигации с нулевым купоном со сроком исполнения T₂ в момент Т₁.

Показатель P используется в этой модели как дисконтный множитель для определения в данный момент времени текущего значения будущих процентов.

В общем виде Pⁱ_t (T) – цена облигации с нулевым купоном со сроком исполнения T в момент t и при i рыночной ситуации. Для придания образа дисконтного множителя при данных процентных ставках, в свою очередь, используется формула



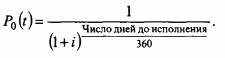
В этой модели стоимость процентного фьючерса принимается не в виде разности (см. главу 8), а в размере собственно процентной ставки.

О "базисе" в технологиях фьючерсов. При разнице курсов, используемых во фьючерсах с относительно более длинными и короткими сроками исполнения, разрыв в курсах обозначается как спрэд (Spread). Теоретически размер Spread равен расходам (Cost-of-Carry), требуемым для осуществления более длительных контрактов. Арбитраж (спекуляция) в этом варианте предполагает продажу более дорогого фьючерса и одновременную покупку более дешевого фьючерса.

Кассовый и срочный рынки находятся (применительно) к фьючерсам в равновесии, если "базис" (срочный курс – кассовый курс) точно соответствует Cost-of-Carry (CoC, см. главу 8), и тогда цена фьючерса является справедливой (равновесной).

На неравновесном рынке цена фьючерса, предлагаемая каждым участником торгов, сложилась под воздействием ожиданий, текущих событий, ликвидности, соотношения спроса и предложения и т.д. Соответственно появляется второй элемент "базиса" (см. главу 9) – оценка "базиса" (Value-Basis). Тогда

Basis ("базис") = (Carry - Basis) + (Value - Basis), равновесный "базис" + оценка "базиса".

Соответственно может быть и "базисный" риск.




¹ См.: Janfien, Birgit / Rudolph, Bernd. Deutsche Aktienindex DAX. Konstruktion und Anwendungsmoglichkeiten. – Frankfurt am Main, 1992. – S. 59.

² См.: Stoll, Hans / Whaley, Robert E. Futures and Options. Theory Applications. Cincinnati, – Ohio, 1993. – P. 160.

³ Но Т./Lee S. Term Structure Movements and Pricing Interest Rate Contingent Claims // Journal of Finance. – 1986. – Vol. 41 – P. 1011–1029. Рассматриваются облигации, поставленные (полученные) при исполнении фьючерса с фиктивным базисом (Cheapest-to-Deliver- или CTD-облигации).


Приложение 13