А. М. Мубараков

Вид материала

Содержание

1.1.6 Сложение гармонических колебаний
A — амплитуда результирующих колебаний, а φ
А результирующих колебаний зависит от разности начальных фаз (φ
С колеблется вдоль отрезка С
Третий закон Ньютона
F = 0 и считая, что скорость выбрасываемых газов относительно ракеты постоянна (ракета движется прямолинейно), получим m dv/dt =
С определяют из начальных условий. Если в начальный момент времени скорость ракеты равна нулю, а ее стартовая масса m

Подобный материал:

1 2 3 4 5 6 7 8 9 10 ... 48

1.1.6 Сложение гармонических колебаний

а) Сложение гармонических колебаний, направленных вдоль одной прямой. Прежде чем рассматривать сложение колебательных движений, остановимся на способе представления колебаний посредством вращающегося вектора амплитуды. Пусть гармоническое колебание можно описать уравнением:

х = A cos (ωt+ φ₀)

(1.58).

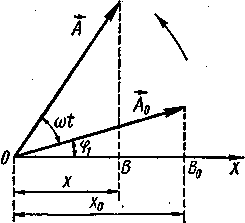
Проведем прямую линию ОХ, которую условно назовем «опорной», и построим вектор А₀, численно равный амплитуде А и направленный из точки О под углом φ к опорной линии (рисунок - 1.20). Если начальная фаза положительна, то угол φ откладывается от опорной линии в сторону, противоположную вращению часовой стрелки; если начальная фаза отрицательна, то угол φ откладывается по часовой стрелке. Проекция вектора А₀ на опорную линию равна смещению х₀ в момент начала отсчета времени (t =0): х₀ = А соsφ₁. Будем вращать вектор амплитуды вокруг оси О, перпендикулярной к плоскости чертежа, с угловой скоростью ω (против часовой стрелки, если ω>0). За промежуток времени t вектор амплитуды повернется на угол ωt и займет положение, изображенное на рисунке - 1.21 вектором А. Его проекция х на опорную линию равна

x = A cos (ωt +φ₁)

(1.59).

За время T, равное периоду колебаний, вектор амплитуды повернется на угол 2π, а проекция В его конца совершит одно полное колебание около положения равновесия О. Следовательно, вращающийся вектор амплитуды полностью характеризует гармоническое колебание.

Пусть точка одновременно участвует в двух гармонических колебаниях одинакового периода, направленных вдоль одной прямой. Сложение этих колебаний удобно производить, пользуясь методом векторных диаграмм. Пусть колебания заданы уравнениями: x₁ = A₁ cos (ωt + φ₁), x₂ = A₂cos (ωt +φ₂). Так как

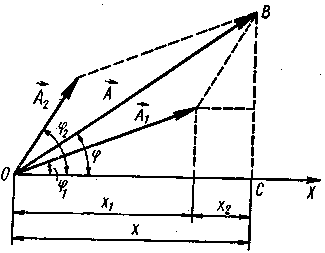
колебания совершаются вдоль одной прямой, то и результирующие колебания будут происходить вдоль этой же прямой. Отложим из точки O опорной линии под углом φ₁ вектор амплитуды А₁и подуглом φ₂ вектор амплитуды А₂ (рисунок - 1.21). Оба вектора вращаются против часовой стрелки с одинаковой угловой скоростью ω, поэтому угол (φ₂-φ₁₎ между ними все время остается неизменным.


Рисунок - 1.20	Рисунок - 1.21

Результирующие колебания могут быть изображены вектором амплитуды А, равным сумме векторов A₁и А₂: А = А₁ + А₂ и вращающимся вокруг точки О с той же угловой скоростью ω, что и векторы А₁ и А_2.. Результирующие колебания должны быть гармоническими с циклической частотой ω:

х = A cos ((ωt + φ)

(1.60),

где A — амплитуда результирующих колебаний, а φ— их начальная фаза. Из рисунка - 1.21 видно, что

А² = А₁² + A₂² + 2А₁А₂ cos (φ₂ - φ₁),

(1.61)

а начальная фаза φ определяется из соотношения tg φ = ВС/ОС, или

tg φ = (А₁ sin φ₁ + А₂ sin φ₂)/(А₁cos φ₁+ А₂cos φ₂)

(1.62).

Из выражения для амплитуда следует, что амплитуда А результирующих колебаний зависит от разности начальных фаз (φ₂-φ₁₎складываемых колебаний. Так (φ₂-φ₁₎с течением времени изменяется, то можно получить определенное значение амплитуды А. Косинус любого угла не может быть больше (+1) и меньше (-1). Следовательно, возможные значения А заключены в пределах ±1:

(А₁ + А₂)≥А≥(А₂- А₁)

(1.63).

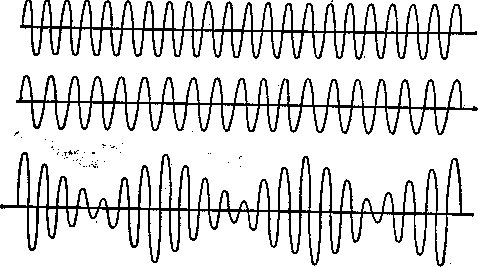
Рассмотрим несколько частных случаев. Если амплитуд двух гармонических колебаний, направленных вдоль одной прямой, одинаковы, а их частоты мало отличаются друг от друга, то в результате сложения этих колебаний получаются колебания с периодически изменяющейся амплитудой. Происхождение этого явления легко представить себе из следующих рассуждений. Пусть в начале колебаний совпадают по фазе и амплитуда результирующего колебания равна сумме их амплитуд. Затем второе колебание начинает отставать по фазе от первого и амплитуда результирующего колебания убывает. Когда разность фаз слагаемых колебаний достигнет определенной величины, результирующая амплитуда станет равной разности амплитуд составляющих колебаний, т. е. в рассматриваемом случае будет равна нулю. При дальнейшем увеличении разности фаз амплитуда, результирующего колебания снова возрастает и, при разности фаз, равной 2π, становится равной сумме амплитуд и т. д. (рисунок - 1.22).

Рисунок - 1.22

Периодические изменения амплитуды от минимального значения до максимального называют биениями. Частота биений равна разности частот складываемых колебаний. Явление биений часто наблюдается при звуковых и электрических колебаниях. Демонстрировать биения можно, заставив одновременно звучать два камертона, обладающих несколько различными частотами свободных колебаний.

Колебания вида х = A(t) cos [ωt + φ(t)] называют модулированными. Различают амплитудно-модулированные колебания, у которых dA/dt«ωA_макс и φ = const, где А_макс — наибольшее значение амплитуды, и колебания, модулированные по фазе или частоте, у которых А=const и dφ/dt«ω.

Биения представляют собой простейший пример модулированных колебаний, у которых A(t) и φ(t) — периодические функции времени. Важной задачей теории колебаний является гармонический анализ (спектральный анализ), т. е. представление сложных модулированных колебаний в виде ряда простых гармонических колебаний.

В общем виде эта задача была разрешена французским математиком Ж. Фурье, который показал, что любые сложные периодические колебания можно представить в виде ряда простых гармонических колебаний с кратными периодами:

х = f{t) = А₀ + А₁ sin (ωt + φi) + + А₂ sin {2ωt + φ₂) + A₃ sin (3ωt + φ₃) + + A_n sin (nωt + + φ_n) + ,

(1.64),

где х = f(t) — функция, описывающая сложное колебание. Число членов в ряду Фурье, вообще говоря, бесконечно велико. Однако возможны такие колебания, для которых ряды Фурье не содержат некоторых членов.

б) Сложение взаимно перпендикулярных колебаний. Пусть материальная точка одновременно участвует в двух гармонических колебаниях, совершающихся с одинаковыми периодами Т в двух взаимно перпендикулярных направлениях. С этими направлениями можно связать прямоугольную систему координат XОY, расположив начало координат в положении равновесия точки (рисунок - 1.23). Обозначим смещение точки С вдоль осей ОХ и OY, соответственно, через х и у. Чтобы найти положение точки в какой-нибудь момент времени t, надо для этого момента времени найти ее смещения, х и у и построить на них прямоугольник (рисунок - 1.23). Конец диагонали прямоугольника определит положение колеблющейся точки в момент времени t, а отрезок ОС — результирующее смещение S. Рассмотрим несколько частных случаев.

а) Начальные фазы колебаний одинаковы. Выберем момент начала отсчета времени таким образом, чтобы начальные фазы обоих колебаний были равны нулю. Тогда смещения вдоль осей ОХ и 0Y можно выразить уравнениями х = А₁ sin ωt, у = А₂ sinωt. Поделив почленно эти равенства, получим уравнение траектории точки С:

x/y = А_1/ А₂ или y = (А₂/ А₁) x

(1.65).

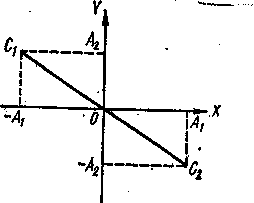
Следовательно, в. результате сложения двух взаимно перпендикулярных колебаний точка С колеблется вдоль отрезка С₁С₂ прямой, проходящей через начало координат (рисунок - 1.23). Такие колебания называют линейно поляризованными.

б) Начальная разность фаз равна π. Уравнения колебаний в этом случае имеют вид:

х =А₁ sin (ωt+ π) = - A₁ cosωt, у =A₂ sin ωt

(1.66).

Уравнение траектории точки С

y =( A₂/ A₁)x

(1.67).

Следовательно, точка С колеблется вдоль отрезка C₁C₂ прямой, проходящей через начало координат, но лежащей в других квадрантах, чем в первом случае (рисунок - 1.24).


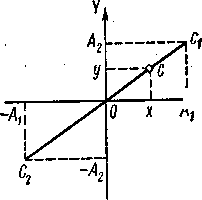Рисунок - 1.23	Рисунок - 1.24

Амплитуда А результирующих колебаний в обоих рассмотренных случаях равна:

А = √А₁²₊ А₂²

(1.68).

При начальной разность фаз π/2 получим случай так называемых эллиптически поляризованных колебаний.

Различные кривые, получаемые при сложении взаимно перпендикулярных колебаний, принято называть фигурами Лиссажу. Форма этих кривых зависит от соотношения амплитуд, частот и начальных фаз колебаний. Поэтому в простейших случаях частоты двух взаимно перпендикулярных гармонических колебаний можно сравнивать по форме фигур Лиссажу. На рисунке - 1.25 показана одна из простейших траекторий, получающаяся при отношении частот 1:2 и разности фаз π/2. Уравнения колебаний имеют вид

х = a cos ωt, y = bcos 2ωt

(1.69).

За то время, пока вдоль оси х точка успевает переместиться из одного крайнего положения в другое, вдоль оси у, выйдя из нулевого положения, она успевает достигнуть одного крайнего положения, затем другого и вернуться в нулевое положение. Чем ближе к единице рациональная дробь, выражающая отношение частот колебаний, тем сложнее оказывается фигура Лиссажу. На Рисунок - 1.26 для примера показана кривая для отношения частот 3:4 и разности фаз π/2.

1.2 Динамика материальной точки

1.2.1 Законы Ньютона. Масса, сила. Закон сохранения импульса, реактивное движение

Раздел физики, изучающий движение тел совместно с причинами его вызывающими, называют динамикой. Механика движения со скоростями v«c, т.е., движение медленных тел, исследуется в классической механике, в основе которой лежат представления Ньютона, сформулированные в трех его законах.


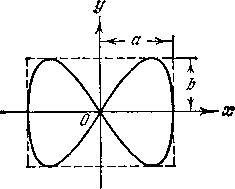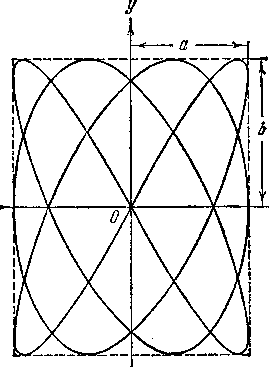Рисунок - 1.25	Рисунок - 1.26

Первый закон Ньютона утверждает: всякое тело находится в состоянии покоя или равномерного и прямолинейного движения, пока воздействие со стороны других тел не заставит его изменить это состояние. В этом законе предполагается, во-первых, что рассматриваемое тело — абсолютно твердое, во-вторых, речь идет только о поступательном движении абсолютно твердого тела в отсутствие внешних воздействий.

Значимость первого закона Ньютона заключается в том, что здесь допускается существование в природе особого явления – сохранения любым телом состояния покоя или равномерного и прямолинейного движения. Это явление Ньютон назвал инерцией. Этим свойством - сохранения состояния покоя или равномерного и прямолинейного движения, обладают все тела, поэтому для ее характеристики пользуются понятием инертность тела. Так как данное свойство выражено у разных тел по-разному, то количественного выражения степени выраженности свойства - сохранения состояния покоя или равномерного и прямолинейного движения было введено понятие массы – как меры инертности тел. Масса – мера инертности тел.

Первый закон Ньютона выполняется не во всякой системе отсчета. Система, отсчета, в которой выполняется первый закон Ньютона, называется инерциальной. Система отсчета, где первый закон Ньютона не выполняется, называется неинерциальной системой отсчета. Первый закон Ньютона называют иногда законом инерции.

Любая система отсчета, движущаяся относительно некоторой инерциальной системы прямолинейно и равномерно будет также инерциальной. Поэтому, инерциальных систем отсчета существует бесконечное множество. Во всех инерциальных системах отсчета движение данной системы тел описываются одними и теми же уравнениями. Поэтому, если в различных инерциальных системах координат мы будем производить одни и те же механические опыты, то эти опыты во всех случаях дадут один и тот же результат. Это положение, высказанное впервые Галилеем, носит название принципа относительности Галилея. Из принципа относительности Галилея следует: никакие механические опыты, производимые внутри инерциальной системы, не дают возможности решить вопрос, имеет ли вся эта система в целом прямолинейное равномерное движение или же она находится в покое. Другим следствием принципа относительности является положение, что в мире не существует абсолютно неподвижного тела: всякий «покой» является относительным.

В содержании первого закона Ньютона характеризуется условие, при котором тело сохраняет свое состояние (покоя или равномерного и прямолинейного движения) неизменным, если на это тело не действуют другие тела. Во втором законе Ньютон отвечает на вопрос, а что будет, если на это тело воздействует другое тело. Оказывается, что при этом происходит изменение скорости этого тела: воздействие на данное тело других тел вызывает изменение его скорости, т. е. выводит его из состояния покоя или прямолинейного движения, т.е. сообщает данному телу ускорение a. Для характеристики такого действия тел друг на друга было введено понятие силы. Силой называют физическую величину, являющуюся мерой механического действия на это тело со стороны других тел.

С помощью, уже введенных в научный оборот, понятий массы m и силы F, содержание второго закона Ньютона можно выразить следующей формулой:

a = F/m

(1.70).

Таким образом, второй закон Ньютона утверждает: ускорение, приобретаемое материальной точкой (телом) прямо пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально его массе. Более употребительно другая форма записи этого закона:

F =m a

(1.71).

Полученное уравнение называют основным законом динамики поступательного движения.

Пусть в начале (t = 0 ) тело обладало скоростью v₀.Под действием силы F за время ∆t = t скорость тела измениласьи стала равной к концу воздействия - v, т.е. a = (v – v₀)/t. Подставим в выражение второго закона Ньютона и преобразуем его:

F =m a = m(v – v₀)/t = (mv – mv₀)/∆t

(1.72).

Анализ полученного соотношения показывает, что сила прямо пропорционально разности произведений - Р = mv, которую назвали импульсом тела.

F = (mv – mv₀)/t = (Р₂- Р₁)/ ∆t =∆Р/∆t

(1.73),

где Р₂и Р₁ конечный и начальный импульсы тела, а (Р₂- Р₁) = ∆Р изменение импульса тела, которое произошло за время ∆t. Выражение (1.73) называется уравнением движения тела и представляет собой общую формулировку второго закона Ньютона: скорость изменения импульса тела равна действующей на нее силе.

Cила - величина векторная. Если на тело одновременно действуют п сил F₁, F₂, , F_nприложенных в одной и той же точке А тела, то их можно заменить одной эквивалентной им силой F, равной их геометрической сумме: F = ∑ F_i , и приложенной в той же точке А. Силу F называют результирующей, или равнодействующей силой. Очевидно, что силы, приложенные в одной и той же точке тела, взаимно уравновешиваются в том и только в том случае, если результирующая этих сил равна нулю. Действие силы на абсолютно твердое тело не изменяется при переносе ее точки приложения вдоль линии действия силы. Если на материальную точку одновременно действуют несколько сил, то каждая из них сообщает материальной точке такое же ускорение, как если бы других сил не было. Это утверждение называют принципом независимости действия сил.

Опыты показывают, что механическое воздействие двух тел друг на друга всегда представляет собой их взаимодействие: если тело 1 действует на тело 2, то при этом тело 2 в свою очередь действует на тело 1. На основе количественного анализа механического взаимодействия тел Ньютон установил свой третий закон: действия двух тел друг на друга всегда равны по величине и направлены по одной прямой в противоположные стороны, т. е.

F₁₂= - F₂₁

(1.74).

Здесь F₁₂— сила, действующая на первое тело со стороны второго, а F₂₁— сила, действующая на второе тело со стороны первого. Следует отметить, что силы F₁₂ и F₂₁ приложены к разным телам и потому не уравновешивают друг друга.

Третий закон Ньютона является существенным дополнением к его первому и второму законам. Он позволяет перейти от динамики отдельной материальной точки к динамике произвольной системы материальных точек, т.е. произвольной механической системы. Для ее описания в динамике широко пользуются понятием центра инерции механической системы. Центром инерции, или центром масс, системы материальных точек называют такую точку С, положение которой задается радиусом-вектором

r_c=(∑m_ir_i)/∑m_i= (1/m) ∑ m_ir_i

(1.75),

где m_t и r_i_; — масса и радиус-вектор i-й точки системы, т — общая масса всей системы, а п — число материальных точек, входящих в состав системы. Скорость центра инерции системы

v_c = dr_c/dt = (1/m) ∑ m_i dr_i/dt = (1/m)∑m_i v_i

(1.76),

где v_i — скорость i-й материальной точки.

Систему материальных точек (тел), не входящих в состав рассматриваемой механической системы, называют внешними телами, а силы, действующие на систему со стороны этих тел,— внешними силами. Соответственно, силы взаимодействия между материальными точками, принадлежащими рассматриваемой системе, называют внутренними силами.

Механическую систему называют замкнутой, или изолированной, если на нее не действуют внешние силы, т. е. происходит взаимодействие только между точками, образующими данную механическую систему. Для замкнутой системы сумма всех внешних сил равна нулю. Отсюда следует закон сохранения импульса: импульс замкнутой системы остается постоянной, какие бы процессы не происходили в этой системе:

dР/dt = 0, Р = ∑m_iv_i= const

(1.77),

где m_i и v_i — масса и скорость i-ой материальной точки системы.

Закон сохранения импульса является одним из основных законов природы. Мы получили его как следствие законов Ньютона. Однако это вовсе не означает, что закон сохранения импульса имеет место лишь в тех пределах, в каких выполняются законы Ньютона и построенная на них классическая механика. Этот фундаментальный закон природы, как показывается в теоретической физике, является следствием определенного физического свойства пространства — его однородности. Однородность пространства означает, что параллельный перенос ^;в нем замкнутой системы как целого не должно отражаться на физических свойствах системы и законах ее движения.

До сих пор мы предполагали, что масса тела остается постоянной, так как само тело не изменяется в процессе его движения. Однако это условие далеко не всегда выполняется. Например, продукты сгорания запасенного в ракете топлива выбрасываются из сопла ракетного двигателя, и масса ракеты уменьшается по мере сгорания топлива.

Идея применения реактивной силы для создания летательных аппаратов высказывалась в 1881 г. Н. И. Кибальчичем. К.Э.Циолковский в 1903 г. опубликовал статью, где предложил теорию движения ракеты и основы теории жидкостного реактивного двигателя. Поэтому его считают основателем отечественной космонавтики.

Рассмотрим движение ракеты, на которую не действуют никакие внешние силы. Полагая F = 0 и считая, что скорость выбрасываемых газов относительно ракеты постоянна (ракета движется прямолинейно), получим m dv/dt = – u dm/dt

откуда v = -u∫ dm/m =-u lnm + C. Значение постоянной интегрирования С определяют из начальных условий. Если в начальный момент времени скорость ракеты равна нулю, а ее стартовая масса m₀, то С = u lnm₀. Следовательно,

v = u ln(m₀/m)

(1.78).

Это соотношение называется формулой Циолковского. Она показывает, что:

1) чем больше конечная масса ракеты т, тем больше должна быть стартовая масса ракеты m₀;

2) чем больше скорость истечения и газов, тем больше может быть конечная масса при данной стартовой массе ракеты.

Все соотношения получены для нерелятивистских движений, т. е. для случаев, когда скорости v и u малы по сравнению со скоростью света с.

Уравнение поступательного движения тела переменной массы впервые было предложено профессором Петербургского университета И. В. Мещерским (1897). Для вывода этого уравнения воспользуемся дифференциальным уравнением для поступательного движения системы, состоящей из тела переменной массы и присоединяющихся или отделяющихся от него частиц. И. В. Мещерский показал, что для тела переменной массы m, движущегося поступательно, имеет место следующее уравнение движения:

d(mv)/dt = F+ (dm₁/dt) • v₁ – d(m₂/dt) • v₂

(1.79),

где v — скорость тела, F - вектор внешних сил, m₁— масса, присоединяющаяся к телу, m₂— масса, отделяющаяся от тела, v₁ и v₂— скорости этих масс. В случае если v₁ и v₂равны нулю, это уравнение переходит в следующее: d(mv)/dt = F

При изучении реактивного движения (когда имеются только отделяющиеся массы) удобно уравнение движения преобразовать к виду: ma = F+ dm₂/dt • (v- v₂), где a — ускорение тела, (v- v₂)— скорость присоединяющихся или отделяющихся частиц по отношению к телу, называемая их относительной скоростью. Уравнение движения тела переменной массы имеет вид

ma = F + F_p,

(1.80)

где a — ускорение тела, а дополнительную силу F_p = dm₂/dt•(v- v₂), обусловленную переменностью массы тела, называют реактивной силой.

Таким образом, было получено уравнение движения тела переменной массы, которое впервые было выведено И. В.Мещерским (1859—1935).

Идея применения реактивной силы в летательных аппаратов высказывалась уже давно. В современных авиационных реактивных двигателях воздух, поддерживающий сгорание топлива, нагнетается специальными насосами. Насос приводится в движение турбиной, действующей за счет струи газа, вытекающего из камеры сгорания. Реактивное действие струи создает полезную тягу двигателя. Такой двигатель носит название турбореактивного двигателя. Авиационный турбореактивный двигатель отличается от простого реактивного двигателя, употребляемого на ракете, тем, что в нем для сгорания топлива используется кислород атмосферного воздуха, а не окислитель, который наряду с горючим несет в своих баках ракета. Благодаря этому, общая масса горючего для турбореактивного двигателя значительно меньше, чем для реактивного. Это преимущество турбореактивного двигателя делает его более пригодным для самолетов, чем простой реактивный двигатель. Однако, турбореактивный двигатель не может работать на очень больших высотах, где плотность атмосферы слишком мала. Он не пригоден для полетов, выходящих за пределы земной атмосферы.

Вопросам ракетной техники и применению ракет для межпланетных сообщений была посвящена вся жизнь выдающегося ученого и изобретателя К. Э. Циолковского. Уже в 1903 г. он опубликовал статью, в которой была рассмотрена теория движения ракеты и впервые были даны основы теории жидкостного реактивного двигателя.

Современные искусственные спутники Земли и космические ракеты выводятся на орбиту с помощью многоступенчатых ракет, так как в случае одноступенчатой ракеты была бы слишком велика масса, которой надо сообщить космическую скорость. Принцип многоступенчатой ракеты был впервые выдвинут К. Э. Циолковским. Ракета использует химическое топливо, причем каждая ступень ракеты имеет свои баки для горючего и окислителя. Схема движения трехступенчатой ракеты состоит в следующем: вначале происходит сгорание топлива в двигателе первой ступени, при этом приводится в движение вся ракета, как целое. Когда топливо первой ступени оказывается использованным, она отделяется, и дальнейший полет ракеты продолжается за счет работы двигателя второй ступени. По окончании работы двигателя второй ступени она отделяется, в свою очередь, и полет продолжает одна третья ступень, масса которой значительно меньше начального ее значения.

Теория воздушно-реактивного двигателя впервые была опубликована в 1929 г. академиком Б. С. Стечкиным. Из-за ряда технических трудностей широкое развитие реактивной и ракетной техники началось лишь в период второй мировой войны и особенно после ее окончания. Применение реактивных двигателей в авиации позволило во много раз увеличить скорости самолетов. Например, скорость современного транспортного самолета ТУ-144 в четыре раза превосходит скорость истребителей с поршневыми двигателями внутреннего сгорания, применявшихся в период второй мировой войны и составляет около 2500 км/ч.

Ракетная техника явилась той базой, на основе которой стали возможными запуски искусственных спутников Земли, пилотируемых космических кораблей и автоматических орбитальных, лунных и межпланетных станций.

Blog

Содержание

1.1.6 Сложение гармонических колебаний