Титульный лист программы Форма обучения по дисциплине ф со пгу 18. 3/37 (Syllabus)
| Вид материала | Программа |
- Титульный лист программы Форма обучения по дисциплине ф со пгу 18. 3/37 (Syllabus), 487.77kb.
- Титульный лист программы Форма обучения по дисциплине ф со пгу 18. 3/37 (Syllabus), 563.5kb.
- Титульный лист программы Форма обучения по дисциплине ф со пгу 18. 3/37 (Syllabus), 602.25kb.
- Титульный лист программы обучения по дисциплине Форма (Syllabus) ф со пгу 18. 3/37, 209.49kb.
- Титульный лист программы Форма обучения по дисциплине ф со пгу 18. 3/37 (Syllabus), 268.51kb.
- Титульный лист программы Форма обучения по дисциплины ф со пгу 18. 3/37 (Syllabus), 309.59kb.
- Титульный лист программы обучения по дисциплине (Syllabus) ф со пгу 18. 3/37, 274.92kb.
- Титульный лист программы обучения по дисциплине (Syllabus) ф со пгу 18. 3/37, 429.81kb.
- Титульный лист программы обучения по дисциплине syllabus ф со пгу 18. 3/37, 881.28kb.
- Титульный лист программы обучения по дисциплине (Syllabus) Форма, 524.99kb.
Титульный лист программы Формаобучения по дисциплине Ф СО ПГУ 7.18.3/37
(Syllabus)
Министерство образования и науки Республики Казахстан
Павлодарский государственный университет им. С. Торайгырова
Факультет физики, математики и информационных технологий
Кафедра Математики
программа обучения по дисциплине
(Syllabus)
Алгебра II
для студентов специальности 5В060100 «Математика»
Павлодар
Лист утверждения программы Форма
обучения по дисциплине Ф СО ПГУ 7.18.3/38
(Syllabus)
УТВЕРЖДАЮ
Декан ФФМиИТ
_____________ Ж.К. Нурбекова.
«___»_________________2010 г.
Составитель д.п.н., профессор ПГУ им. С.Торайгырова Дроботун Б.Н. ________
Кафедра математики
Программа обучения по дисциплине (Syllabus)
Алгебра II
для студентов очной формы обучения
специальности 5В060100 «Математика»
Программа разработана на основании рабочей учебной программы, утверждённой
«____» _________20___г.
Рекомендована на заседании кафедры от «___»____________20__г.
Протокол №_____.
Заведующий кафедрой ______________________ И.И.Павлюк
Одобрена учебно-методическим советом ФФМиИТ
«_____»______________20___ г. Протокол №____
Председатель УМС___________________ Ж.Г. Муканова. «_____»_________20___ г.
1. Сведения о преподавателе и контактная информация
Дроботун Борис Николаевич – кандидат физико-математических наук, доктор педагогических наук, доцент ВАК, профессор ПГУ им. С. Торайгырова.
Кафедра математики находится в 1 корпусе, аудитория № 201.
2 Данные о дисциплине
Алгебра – часть математики, посвященная изучению алгебраических операций. Основной задачей изучения алгебраических операций и их совокупностей в современной математике является задача изучения специфики действия этих операций, при этом, множества, на которых они задаются, играют второстепенное значение. В соответствии с этим, операции задаются системами аксиом, в которых посредством их синтаксического строения характеризуются свойства этих операций.
Простейшие алгебраические операции – арифметические действия над натуральными и положительными рациональными числами – встречаются в самых ранних математических текстах, свидетельствующих о том, что уже в глубокой древности были известны все основные свойства этих действий.
В 17-18 вв. под алгеброй понималась наука о буквенных вычислениях – тождественных преобразованиях буквенных формул, решения алгебраических уравнений и т.п. – в отличие от арифметики, занимавшейся вычислениями над конкретными числами. Предполагалось, однако, что под буквами подразумеваются числа целые или дробные.
Наряду с теорией алгебраических уравнений с одним неизвестным развивается теория систем алгебраических уравнений с несколькими неизвестными, в частности систем линейных уравнений. В связи с исследованием последних, возникают понятия матрицы и определителя.
Начиная с середины 19 в. центр тяжести в алгебраических исследованиях постепенно перемещается с теории уравнений на изучение произвольных алгебраических операций.
Эти работы подготовили вступление алгебры в конце 19 – начало 20 вв. в современный этап ее развития, характеризующийся объединением ранее разрозненных алгебраических идей на общей аксиоматической основе и существенным расширением области приложений.
3 Трудоемкость дисциплины
| Семестр | Количество кредитов | Количество контактных часов по видам аудиторных занятий | Количество часов самостоятельной работы студентов | Формы контроля | ||||||
| всего | лек | пр | лаб | студ | инд | всего | СРСП | |||
| 1 | 3 | 45 | 15 | 30 | | | | 90 | 6,75 | экз |
| 2 | 3 | 45 | 15 | 30 | | | | 90 | 6.75 | экз |
| Всего | 6 | 90 | 30 | 60 | | | | 180 | 13,5 | |
4 Цель дисциплины:
- формирование общей алгебраической и мировоззренческой культуры, как базовой основы освоение языка современной математики;
- формирование культуры абстрактно-логического мышления, позволяющего овладеть системой идей и методов современной алгебры;
- формирование системы знаний навыков и умений, позволяющей использовать методологию современной алгебры при изучении других математических дисциплин теоретического и прикладного характера.
Задачи дисциплины:
- освоение базовых конструкций и технологий современной алгебры, связанных с гомоморфизмами и изоморфизмами алгебраических систем: подобъектов, расширений объектов, образа и ядра гомоморфизма (оператора); фактор-структуры; конгруэнции и т. п.;
- отработка навыков нахождения собственных значений, векторов и инвариантных подпространств линейного оператора;
- освоение технологий нахождения жордановой формы матрицы.
5. Требования к знаниям, умениям и навыкам
В результате изучения данной дисциплины студенты должны:
иметь представление:
- об операторе как отображении множеств. наделенных теми или иными математическими структурами: алгебраическими, порядковыми, топологическими, метрическими и т.д.
- об алгебре операторов как алгебраической системе относительно алгебраических операций взятия обратного оператора, произведения оператора на число, сложении и умножения операторов.
- о способах задания операторов;
- о нормальных формах однотипных математических объектов, как о наиболее удобных для использовании в математической практике представителях из классов, полученных посредством тех или иных классификационных процедур, определенных на совокупностях этих объектов;
- о теории квадратичных форм, как обобщенно-алгебраической реализации теории линий 2-го порядка аналитической геометрии.
знать:
- понятие линейного преобразования и линейного оператора в линейных и евклидовых пространствах; матрицы линейного оператора; собственного значения, собственного вектора и инвариантного подпространства линейного оператора; понятие корневого подпространства; понятие сопряженного, нормального, ортогонального и симметрического оператора и их алгебраическую и геометрическую характеризации;
- понятие
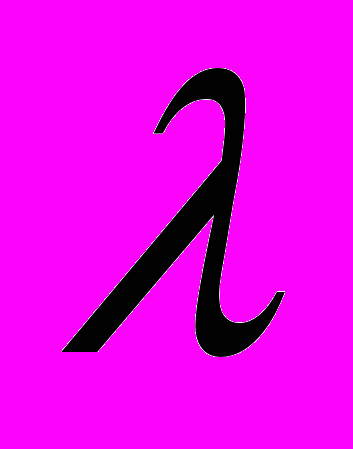- матрицы; алгоритм приведения 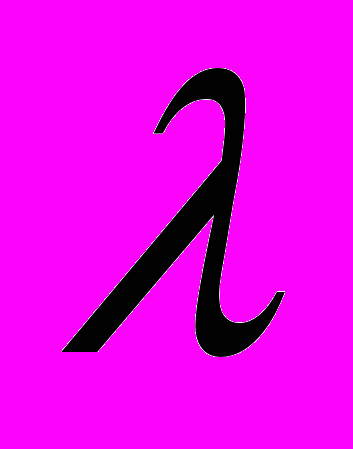- матрицы к каноническому виду; понятие подобия матриц и критерий подобия; понятие жордановой клетки и жордановой матрицы; алгоритм приведения матрицы к жордановой нормальной форме;- понятие квадратичной формы и её матрицы; канонического вида и инвариантов квадратичной формы; понятие знакопостоянной квадратичной формы.
уметь:
- находить матрицу линейного оператора; по матрице линейного оператора, заданной в одном базисе находить матрицы этого оператора при переходе от одного базиса к другому; находить собственные значения, собственные векторы и инвариантные подпространства линейного оператора; строить ортонормированные базисы евклидова пространства из собственных векторов линейного оператора этого пространства;
- раскладывать векторные пространства в прямую сумму корневых подпространств линейного оператора и корневых подпространств в прямую сумму циклических подпространств;
- приводить матрицы к жордановой форме и строить канонические базисы;
- использовать свойства сопряженных, ортогональных, симметрических операторов;
- приводить
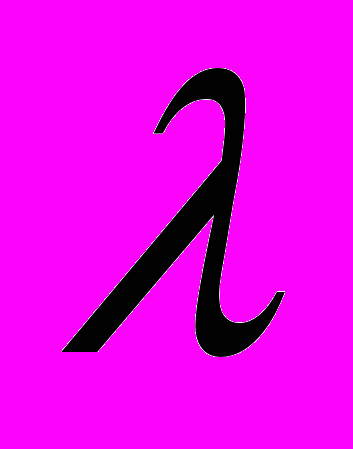- матрицу к каноническому виду различными методами; применять алгоритм приведения матрицы к жордановой нормальной форме;- находить матрицу квадратичной формы (и квадратичную форму по матрице); приводить квадратичную форму к нормальному виду; применять алгоритм Сильвестра положительной определенности квадратичной формы; находить инварианты квадратичной формы.
приобрести практические навыки:
- находить матрицы суммы и произведения линейных операторов; переходить от матрицы линейного оператора, заданной в одном базисе к матрице этого оператора в другом;
- оперирования с квадратичными формами и каноническими алгоритмами их преобразования к тем или иным видам;
- приведения матриц к жордановой нормальной форме .
6 Пререквизиты
Для освоения данной дисциплины необходимы знания, умении и навыки, приобретенные при изучении следующих дисциплин: школьный курс « Алгебра и начала анализа», «Геометрия», вузовский курс «Введение в специальность».
7 Постреквизиты
Знания, умения и навыки, полученные при изучении дисциплины необходимы для освоения следующих вузовских дисциплин: математический анализ, аналитическая геометрия, дифференциальные уравнения, дискретная математика и математическая логика.
8 Содержание дисциплины
Тематический план дисциплины
| № | Наименование тем | Количество контактных часов по видам занятий | |||
| лекц | практ | лаб | СРС | ||
| 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | Линейные операторы в линейных пространствах и операции над ними. | 4 | 6 | - | 18 |
| 2 | Жорданова форма матрицы. | 4 | 10 | - | 24 |
| 3 | Линейные операторы в евклидовых и унитарных пространствах | 3 | 6 | - | 24 |
| 4 | Квадратичные формы. | 4 | 8 | - | 24 |
| ИТОГО : | 15 | 30 | - | 90 | |
9. Краткое описание дисциплины.
В учебном курсе «Алгебра» изучаются посредством применения метода содержательных аксиоматик классические алгебры и алгебраические системы: группы, кольца, поля, векторные пространства. В качестве базовых примеров колец и полей рассматриваются числовые системы, кольца вычетов по модулю т, кольца многочленов над полем, матричные кольца. Пропедевтической основой изучения конечномерных векторных пространств служит п-мерное векторное пространство векторов строк над полем действительных чисел. В рамках изучения векторных пространств изучаются методы исследования и решения систем неоднородных и однородных линейных уравнений. Евклидовы и унитарные пространства размерности п и их преобразования изучаются как обобщение трехмерного пространства с базисом
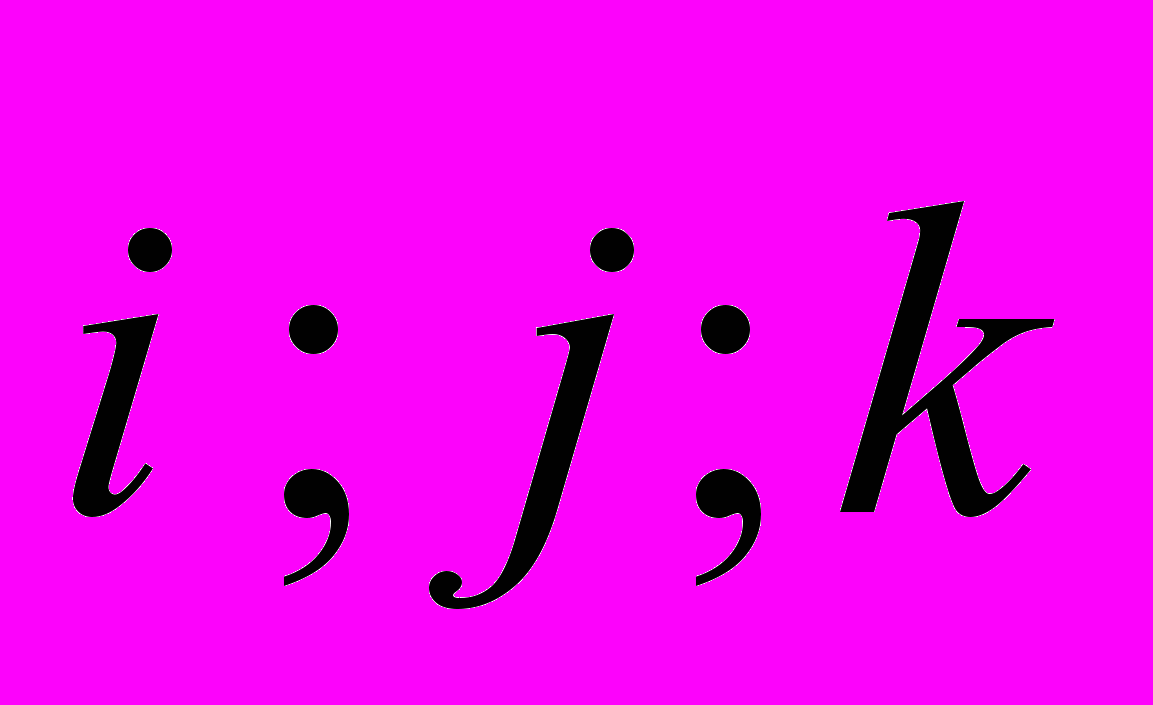и их линейных преобразований.10 Компоненты курса
Перечень тем лекционных занятий
Тема 1. Линейные операторы в евклидовых и унитарных пространствах и операции над ними.
Понятие линейного оператора. Матрицы линейного оператора. Связь между линейными операторами в разных базисах. Образ и ядро, ранг и дефект линейного оператора. Обратимые линейные операторы. Метод параллельного вычисления базиса ядра и образа линейного оператора. Собственные векторы и собственные значения линейного оператора и методы их нахождения. Линейные преобразования с простым спектром. Инвариантные подпространства линейного оператора. Разложение пространства в прямую сумму корневых подпространств линейного оператора. Разложение корневого пространства в прямую сумму циклических подпространств.
Тема 2. Жорданова форма матрицы.
Понятие
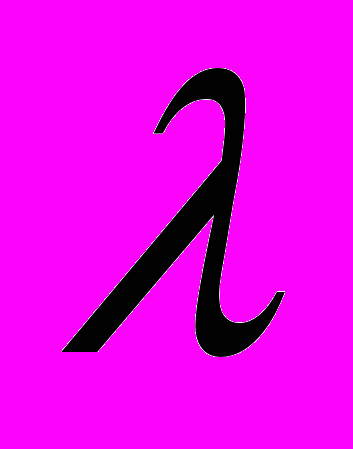- матрицы. Элементарные преобразования 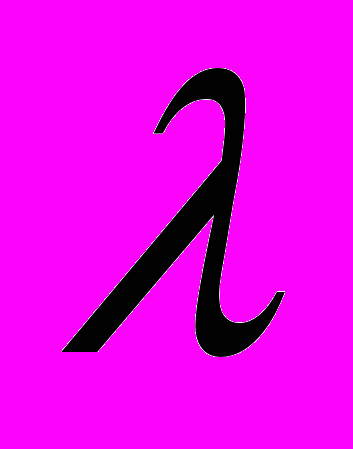- матриц. Канонические 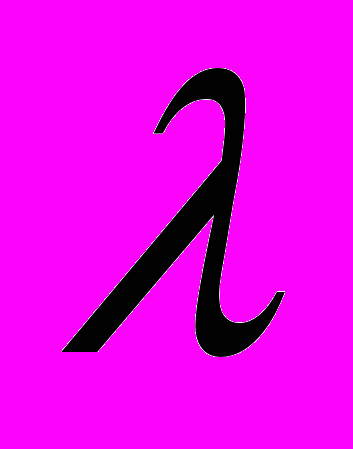- матрицы. Алгоритм приведения 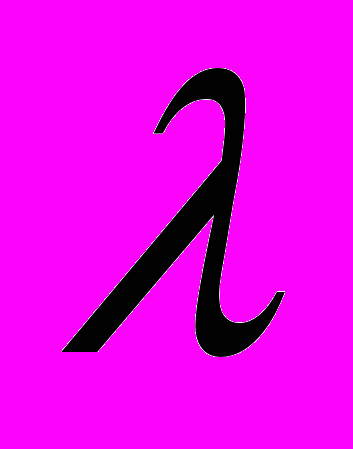- матрицы к каноническому виду посредством элементарных преобразований. Унимодулярные 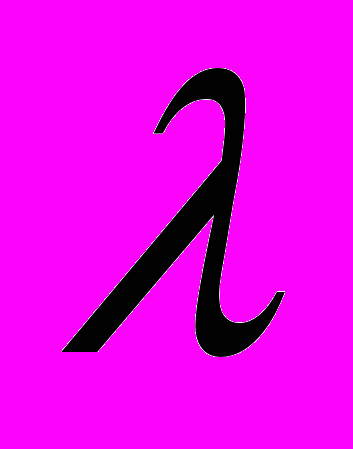- матрицы. Связь подобия числовых матриц с эквивалентностью их характеристических матриц. Матричные многочлены. Теорема о подобии матриц. Жорданова нормальная форма. Приведение матрицы к жордановой нормальной форме. Построение канонического базиса. Тема 3. Линейные операторы в евклидовых и унитарных пространствах.
Линейные функционалы. Сопряженные и нормальные операторы. Критерий нормальности оператора. Унитарные и симметрические операторы. Алгебраическая и геометрическая характеризации унитарных, ортогональных, самосопряженных и знакопостоянных операторов. Полярное разложение. Теорема о полярном разложении.
Тема 4. Квадратичные формы.
Квадратичные формы и их матрицы. Преобразование неизвестных квадратичной формы. Метод Лагранжа приведения квадратичной формы к каноническому виду. Закон инерции, инварианты квадратичной формы. Знакопостоянные квадратичные формы, критерий Сильвестра. Приведение квадратичной формы к главным осям.
Перечень и содержание практических занятий
Тема 1. Линейные операторы в евклидовых и унитарных пространствах и операции над ними.
Занятие 1,2. Матрица линейного оператора.
Решение задач на нахождение матрицы линейного оператора в различных базисах; на нахождение матричных представлений результатов операций над линейными операторами (операций сложения, умножения линейных операторов и операции взятия обратного оператора).
Занятие 3,4. Ранг и дефект линейного оператора.
Решение задач на нахождение ранга и дефекта линейного оператора и на построение базисов его ядра и области значений. Отработка алгоритма на нахождение собственных векторы и собственных значений линейного оператора. Линейные опраторы с простым спектром.
Занятие 5,6. Инвариантные подпространства.
Анализ методов нахождения инвариантных подпространств линейных операторов, на разложение векторного пространства в прямую сумму корневых подпространств линейного оператора и на разложение корневых пространств в прямую сумму циклических подпространств.
Тема 2. Жорданова форма матрицы.
Занятие 7,8. Жорданова форма матриц.
Задачи на реализацию алгоритма приведения матриц к жордановой нормальной форме.
Занятие 9,10.
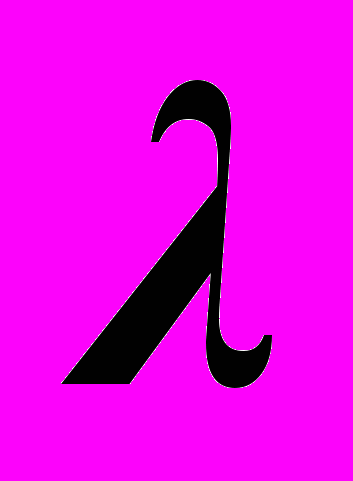- матрицы. Элементарные преобразования
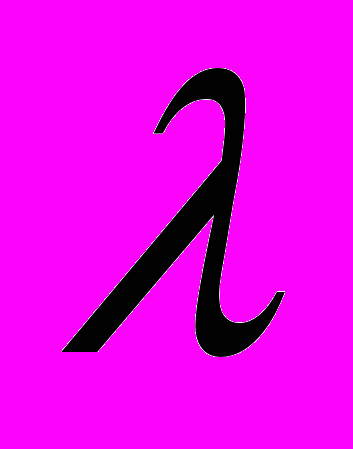- матриц. Отношение эквивалентности 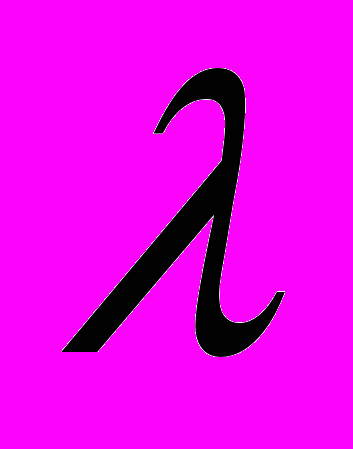- матриц. Канонические 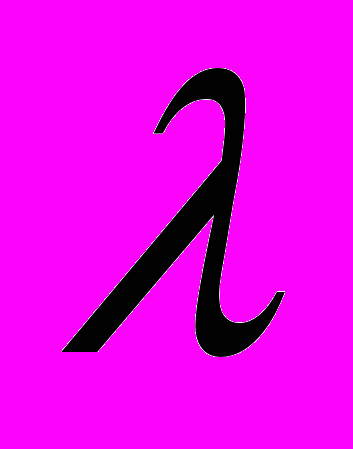- матрицы. Задачи на отработку навыков и умений приведение 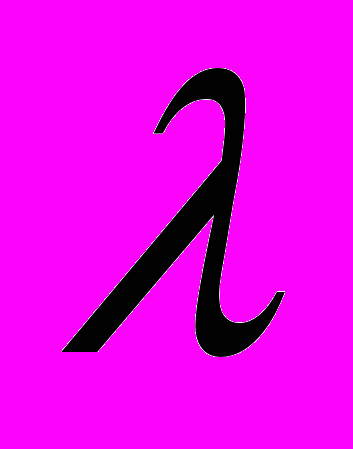- матриц к каноническому виду посредством элементарных преобразований.Занятие 11,12. Унимодулярные матрицы.
Отработка навыков работы с унимодулярными матрицами. Матричные многочлены и
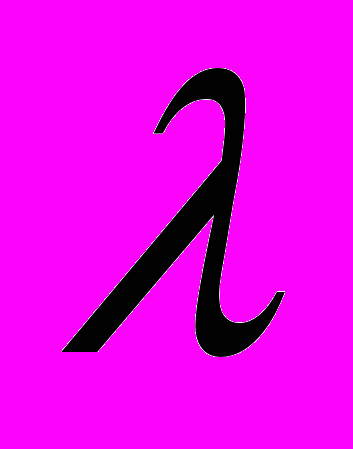- матрицы. Критерий подобия матриц и отработка технологий его применения.Занятие 13,14. Метод
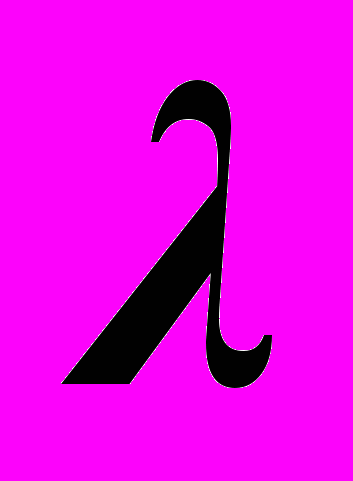- матриц нахождения жордановой формы.Клетки Жордана и их канонический вид. Элементарные делители матрицы А и методы их нахождения. Отработка алгоритма приведения к жордановой нормальной форме.
Занятие 15,16. Минимальный многочлен матрицы.
Многочлены от матриц. Многочлены, аннулируемые матрицей А. Инвариантные множители и минимальный многочлен матрицы А. Алгоритм нахождения минимального многочлена.
Тема 3. Линейные операторы в евклидовых и унитарных пространствах.
Занятие 17,18. Сопряженные и самосопряженные операторы.
Сопряженные операторы и их матрицы. Отработка навыков работы с сопряженными операторами.
Занятие 19,20. Ортогональные операторы.
Матрицы ортогональных операторов. Ортогональные матрицы. Канонический вид ортогональной матрицы. Решение задач на ортогональные преобразования и ортогональные матрицы.
Занятие 21,22. Симметрические и кососимметрические операторы.
Матрицы симметрических и кососимметрических операторов. Решение задач и отработка алгоритмов.
Тема 4. Квадратичные формы.
Занятие 23,24. Матрицы квадратичных форм.
Квадратичные формы и их матрицы. Ранг квадратичной формы. Линейные преобразования переменных квадратичной формы. Решение задач.
Занятие 25,26. Канонический вид квадратичной формы.
Метод Лагранжа приведения квадратичной формы к каноническому виду. Решение задач на применение алгоритма Лагранжа.
Занятие 27,28. Закон инерции.
Положительный, отрицательный индексы инерции и сигнатура квадратичной формы. Решение задач на нахождение инвариантов действительных квадратичных форм.
Занятие 29,30. Положительно определенные квадратичные формы.
Критерий положительной определенности квадратичных форм. Решение задач на применение критерия положительной определенности.
Содержание самостоятельной работы студента
Перечень видов СРС
| № | Вид С.Р.С. | Форма отчетности. | Вид контроля | Объем в часах. |
| 1 | Подготовка к лекционным занятиям. | | Выборочный опрос. | 15 |
| 2 | Подготовка к практическим занятиям (изучение материала по теме занятия, решение задач и упражнений). | Рабочая тетрадь с решениями | Выборочная Проверка. Участие на занятиях. | 30 |
| 3 | Изучение материала, в частности, не вошедшего в аудиторные занятия. | Конспект. Письменные ответы на вопросы по содержанию материала. | Коллоквиум (фронтальная проверка). | 6 |
| 4 | Выполнение индивидуальных заданий. | Тетради для выполнения индивидуальных заданий. | Проверка и собеседование по результатам проверки. | 16 |
| 5 | Подготовка докладов (рефератов) | Компьютерная распечатка доклада. | Допуск к защите и защита реферата. | 6 |
| 6 | Подготовка к выполнению контрольных работ. | Решение заданий соответствующего варианта К.Р. | Проверка Выборочное собеседование. | 12 |
| 7 | Подготовка к выполнению рубежных контрольных мероприятий. | Результаты РК-1 и РК-2. Тестирование и собеседование. | Проверка вариантов тестовых заданий. Собеседование. | 5 |
| Всего | 90 | |||
Перечень тем (разделов, подразделов), вынесенных на самостоятельное изучение студентами
1. Невырожденные линейные операторы.
2. Линейные операторы с простым спектром. Условия, при которых матрица линейного оператора подобна диагональной.
3. Нормальные операторы и критерий нормальности.
4. Геометрическая характеризация ортогональных и самосопряженных операторов.
5. Распадающиеся квадратичные формы.
6. Приведение квадратичной формы к главным осям. Пары форм.
Календарный график контрольных мероприятий
по выполнению и сдаче заданий на СРС и работе на занятиях по дисциплине «Алгебра 2» для студентов очной формы обучения специальности 5В060100 «Математика»
| 1 рейтинг (2семестр) | |||||||||||
| Недели | Макс балл за 1 занятие | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | всего | |
| Максимальный балл | 6 | 6 | 11 | 18 | 10 | 11 | 18 | 20 | 100 | ||
| Посещение и подготовка к лекциям | Вид СРС/ форма отчетн. | | ДЗЛ1 | ДЗЛ2 | ДЗЛ3 | ДЗЛ4 | ДЗЛ5 | ДЗЛ6 | ДЗЛ7 | ДЗЛ8 | 16 |
| Форма контроля | | У | У | У | У | У | У | У | У | ||
| Макс балл | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | ||
| Посещение и подготовка к практ. занятиям | Вид СРС/ форма отчетн. | | ДЗП 1,2 | ДЗП 3,4 | ДЗП 5,6 | ДЗП 7,8 | ДЗП 9,10 | ДЗП 11,12 | ДЗП 13,14 | ДЗП 15,16 | 32 |
| Форма контроля | | У | У | У | У | У | У | У | У | ||
| Макс балл | 2 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | ||
| Выполнение и оформление инд. заданий | Вид СРС/ форма отчетн. | | | | | ИДЗ1 | | | ИДЗ2 | | 16 |
| Форма контроля | | | | | Д,П | | | Д,П | | ||
| Макс балл | | | | | 8 | | | 8 | | ||
| Выполнение и оформление контр. работ | Вид СРС/ форма отчетн. | | | | КР1 | | | КР2 | | | 10 |
| Форма контроля | | | | П | | | П | | | ||
| Макс балл | | | | 5 | | | 5 | | | ||
| Написание и защита доклада/ реферата | Вид СРС/ форма отчетн. | | | | | | Р1 | | | | 4 |
| Форма контроля | | | | | | Д,З | | | | ||
| Макс балл | | | | | | 4 | | | | ||
| Самостоятельное Изучение материала | Вид СРС/ форма отчетн. | | | | | ДЗ СИ1 | | | ДЗ СИ2 | | 8 |
| Форма контроля | | | | | К | | | К | | ||
| Макс балл | | | | | 4 | | | 4 | | ||
| Контроль знаний по темам дисциплины | Вид СРС/ форма отчетн. | | | | | | | | | ПТД | 14 |
| Форма контроля | | | | | | | | | Т | ||
| Макс балл | | | | | | | | | 14 | ||
| 2 рейтинг (2семестр) | |||||||||||
| Недели | Макс балл за 1 занятие | 9 | 10 | 11 | 12 | 13 | 14 | 15 | | всего | |
| Максимальный балл | 6 | 6 | 19 | 12 | 10 | 19 | 28 | | 100 | ||
| Посещение и подготовка к лекциям | Вид СРС/ форма отчетн. | | ДЗЛ9 | ДЗЛ10 | ДЗЛ11 | ДЗЛ13 | ДЗЛ13 | ДЗЛ14 | ДЗЛ15 | | 14 |
| Форма контроля | | У | У | У | У | У | У | У | | ||
| Макс балл | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | | ||
| Посещение и подготовка к практ. занятиям | Вид СРС/ форма отчетн. | | ДЗП 17,18 | ДЗП 19,20 | ДЗП 21,22 | ДЗП 23,24 | ДЗП 25,26 | ДЗП 27,28 | ДЗП 29,30 | | 28 |
| Форма контроля | | У | У | У | У | У | У | У | | ||
| Макс балл | 2 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | | ||
| Выполнение и оформление инд. заданий | Вид СРС/ форма отчетн. | | | | ИДЗ3 | | | ИДЗ4 | | | 18 |
| Форма контроля | | | | Д,П | | | Д,П | | | ||
| Макс балл | | | | 9 | | | 9 | | | ||
| Выполнение и оформление контр. работ | Вид СРС/ форма отчетн. | | | | | КР3 | | | КР4 | | 12 |
| Форма контроля | | | | | П | | | П | | ||
| Макс балл | | | | | 6 | | | 6 | | ||
| Написание и защита доклада/ реферата | Вид СРС/ форма отчетн. | | | | | | Р2 | | | | 4 |
| Форма контроля | | | | | | Д,З | | | | ||
| Макс балл | | | | | | 4 | | | | ||
| Самостоятельное Изучение материала | Вид СРС/ форма отчетн. | | | | ДЗ СИ3 | | | ДЗ СИ4 | | | 8 |
| Форма контроля | | | | К | | | К | | | ||
| Макс балл | | | | 4 | | | 4 | | | ||
| Контроль знаний по темам дисциплины | Вид СРС/ форма отчетн. | | | | | | | | ПТД | | 16 |
| Форма контроля | | | | | | | | Т | | ||
| Макс балл | | | | | | | | 16 | | ||
Условные обозначения: ДЗЛ 1 – домашнее задание на подготовку к лекции №1; У – участие в учебном процессе; ДЗП 1 – домашнее задание на подготовку к практическому занятию №1; Д – допуск; О – отчет; П – проверка; ДЗСИ1 домашнее задание №1 на самостоятельное изучение материала; К – коллоквиум; КР 1 – контрольная работа №1; ИДЗ 1 – индивидуальное задание №1; Т 1 – тест №1, Р – реферат.
Рекомендован на заседании кафедры от «____»____________20___г. Протокол № ____
Заведующий кафедрой ____________ Павлюк И.И. «____»_______20___ г.
11 Политика курса
В обязанности студентов входит регулярное посещение занятий, выполнение требований графика сдачи заданий по дисциплине, самостоятельная работа с литературой в библиотеке и интернет зале.
В процессе совместной работы преподавателей со студентами необходимо придерживаться следующих правил:
1. Преподаватель и студент должны относиться друг к другу с уважением, быть тактичным и вежливым.
2. Будьте активны на занятиях. Задавайте преподавателю вопросы. Присутствие на занятиях не является достаточным. Нужно активное овладение материалом, анализ предлагаемых технологий и установок, выяснение мельчайших подробностей схем, принципов действия и т.п.
3. Преподавтель обязан творчески работать со студентом. Студент обязан идти на контакт с преподавателем и получать консультацию по выполняемым практическим, самостоятельным заданиям.
4. Не стесняйтесь ошибаться. Не ошибается тот, кто ничего не делает.
5. Не делайте вид, что вы во всём разобрались. Проявляйте пытливость, наблю-дательность.
6. Посещение занятий является обязательным. Если вы пропустили три и более занятия без уважительных причин (причина должна быть подтверждена документально), то преподаватель вправе потребовать от вас получения допуска деканата.. Помните: посещаемость входит в итоговую оценку.
7. Необходимо своевременно сдавать отчёты по практическим, самостоятельным работам в соответствии с графиком. Это влияет на итоговую оценку. Незавершенные отчеты и самостоятельные работы не засчитываются. Свовременное и в полной мере выполненное задание предпологает максимаоьный балл за каждую работу.
Поощрительные балы – 5 баллов:
- за творческий подход;
- за активное участие в учебном процессе;
- за участие в студенческой конференций;
- за использование разнообразных источников.
Штрафные баллы – 5 баллов взимаются из общего количества в случае:
- несвоевременного представления материалов;
- некачественно выполненной работы;
- пропуска занятий;
- опоздания на занятия.
Без личного присутствия студента итоговый контроль не проводится.
8. Опоздания на аудиторные занятия допускаются только до 5 минут, в противном случае студент к занятию не допускается. При наличии объективных причин необходимо предупредить преподавателя заранее. Систематические опоздания – признак дурного тона. Они характеризуют отношение студента к учёбе.
9. Этика не допускает разговоров вслух, когда говорит преподаватель. После второго предупреждения студент удавляется из аудитории. Разговоры на посторонние темы во время занятий не допускаются.
10. Ваша обязанность приходить на занятия подготовленным. Используйте имеющуюся литературу, своевременно получите литературу в библиотеке.
11. Правила внутреннего распорядка должны выполняться.
12. Категорически запрещается копирование выполненных чужих работ, заимствование без переработки литературных материалов.
13. Все отчёты представляются в машинописном варианте с индивидуальной переработкой материала и начерченными схемами, устройствами.
14. Желательно посещение консультаций.
15. Во время занятий сотовые телефоны должны быть отключены.
16. Обработка и сдача практических работ, СРС не по графику ухудшает качество усвоения, качество учёбы, создаёт ненужные напряжения и хаос. Для создателя стимула к созидающему ритмичному труду студентов служит рейтинговая карта с поощрением своевременной и качественной работы.
17. Каждый студент должен внимательно ознакомиться с рейтинговой картой и графиками выполнения всех видов работ и выполнять все требования, которые направлены на повышение успеваемости и качество подготовки специалистов.
18. Итоговая оценка подсчитывается по формуле
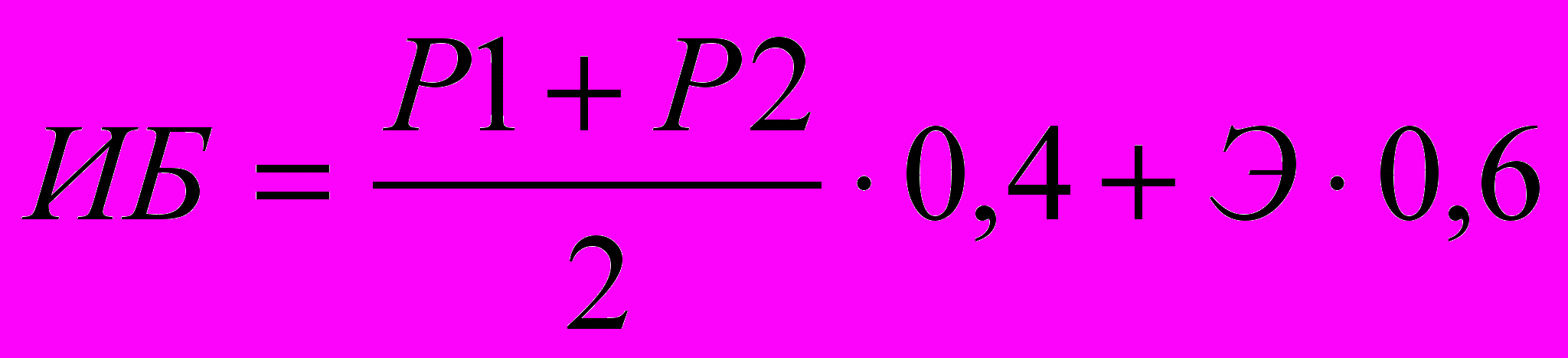
ИБ – итоговый балл.
Р1, Р2 – баллы, полученные на рубежных контролях
Э – балл, полученный на экзамене.
12 Список литературы
Основная
1. Курош А.Г. Курс высшей алгебры: Учебник. М.: Физматлит, 200 Физматлит, 2001.
.
2. Кострикин, А. И. Введение в алгебру: учебник. М.: Физматлит, 2001.
3. Проскуряков И. В. Сборник задач по линейной алгебре: Учебное пособие для физ.-мат. спец. вузов . М.: Лаборатория Базовых Знаний, 2003.
4. Фаддеев Д. К., Соминский И. С. Задачи по высшей алгебре: учеб. пособие для студ. вузов, обучающихся по мат. Спец. СПб.:Лань, 2008.
5. Фадеев Д.К., Соминский Л.С. Сборник задач по высшей алгебре: Учебное пособие, М.: Наука, 1972
Дополнительная
6. Кострикин А. И., Манин Ю. И.. Линейная алгебра и геометрия: учеб. пособие. СПб.:Лань,2008.
7. Икрамов, Х. Д. Задачник по линейной алгебре: учеб. пособие. СПб.:Лань, 2006
8 Воеводин, В. В. Линейная алгебра: учеб. пособие. СПб.:Лань, 2008.