Т. С. Рамазанов доктор физико-математических наук, профессор, Казну им. Аль-Фараби, г. Алматы; > С. К. Тлеукенов доктор физико-математических наук, профессор, пгу им. С. Торайгырова, г. Павлодар; > А. М. Мубараков
| Вид материала | Учебник |
- Титульный лист программы Форма обучения по дисциплине ф со пгу 18. 3/37 (Syllabus), 349.17kb.
- Б. А. – доктор юридических наук, профессор Казну им аль-Фараби, 209.21kb.
- Карпухин В. Б., доктор физико-математических наук, профессор кафедры «Высшая и прикладная, 263.95kb.
- А. М. Мубараков доктор пед наук, профессор. Н. Э. Пфейфер доктор пед наук, профессор, 1066.25kb.
- Веселаго Виктор Георгиевич, доктор физико-математических наук, профессор мфти, область, 30.58kb.
- Практических: 0 Лабораторных, 16.69kb.
- Практических: 34 Лабораторных, 24.5kb.
- Практических: 0 Лабораторных, 16.63kb.
- Практических: 34 Лабораторных, 20.05kb.
- Практических: 0 Лабораторных, 18.53kb.
1.2.2 Силы в механике
В современной физике различают четыре вида взаимодействий:
1) гравитационное (обусловленное всемирным тяготением);
2) электромагнитное (осуществляемое через электрические и магнитные поля);
3) сильное или ядерное (обеспечивающее связь частиц в атомном ядре);
4) слабое (ответственное за процессы взаимопревращений элементарных частиц).
В задачах классической механики встречаются с гравитационными и электромагнитными силами, а также с упругими силами и силами трения. Два последних вида сил определяются характером взаимодействия между молекулами вещества. Силы взаимодействия между молекулами имеют электромагнитное происхождение. Следовательно, упругие силы и силы трения являются по своей природе электромагнитными. Гравитационные и электромагнитные силы являются фундаментальными — их нельзя свести к другим, более простым, силам. Упругие же силы и силы трения не являются фундаментальными. Законы фундаментальных сил чрезвычайно просты. Для упругих сил и сил трения они получены эмпирически.
Под действием приложенных к нему сил всякое реальное тело деформируется, т. е. изменяет свои размеры и форму. Если после прекращения действия сил тело принимает первоначальные размеры и форму, деформация называется упругой. Упругие деформации наблюдаются в том случае, если сила, обусловившая деформацию, не превосходит некоторый, определенный для каждого конкретного тела предел (предел упругости).
Опыт показывает, что при небольших деформациях удлинение пружины ∆х оказывается по величине пропорциональным растягивающей силе: ∆х~Fупр,. Соответственно, упругая сила оказывается пропорциональной удлинению пружины и противодействует ей:
| Fупр. = - k∆х. | (1.81). |
Это соотношение носит название закона Гука, где k называется коэффициентом жесткости пружины.
Силы трения появляются при перемещении соприкасающихся тел или их частей друг относительно друга. Трение, возникающее при относительном перемещении двух соприкасающихся тел, называется внешним (сухим); трение между частями одного и того же сплошного тела (например, жидкости или газа) носит название внутреннего трения. Силы трения, которые возникают при движении твердого тела в жидкой или газообразной среде, следует отнести к категории сил внутреннего трения. В этом случае, слои среды, непосредственно соприкасающиеся с телом, вовлекаются им в движение с той же скоростью, с какой твердое тело движется в этой среде. Трение между поверхностями двух твердых тел при отсутствии какой-либо прослойки, например смазки между ними, называется сухим. Трение между твердым телом и жидкой или газообразной средой, а также между слоями такой среды называется вязким (или жидким).
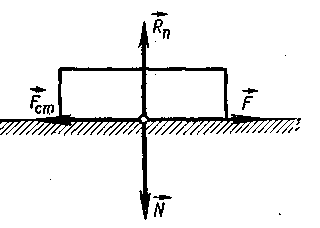
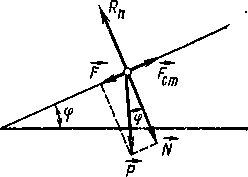
Силы трения направлены по касательной к трущимся поверхностям (или слоям), причем так, что они противодействуют относительному смещению этих поверхностей (слоев). Если, например, два слоя жидкости скользят друг по другу, двигаясь с различной скоростью, то сила, приложенная к более быстро движущемуся слою, направлена в сторону, противоположную движению, а сила, действующая на слой, движущийся медленнее, направлена в сторону движения слоя. Сухое трение возникает не только при скольжении одной поверхности по другой, но также и при попытках вызвать такое скольжение. В последнем случае она называется силой трения покоя. Одно тело прижимается к другому телу с силой Fтр, направленной по нормали к поверхности соприкосновения тел (рисунок - 1.27). Она называется силой нормального давления N и может быть обусловлена весом тела или другими причинами. Cила трения Fтp по модулю равна N, но имеет противоположное направление. Безразмерный коэффициент пропорциональности µ называют коэффициентом трения. Он, как показывает опыт, зависит от материала и состояния поверхностей соприкосновения тел. Если тело находится на наклонной плоскости, то, как видно из рисунка - 1.28
| N = Р cos φ и F = Psin φ | (1.82), |
где Р — сила тяжести тела, φ —угол наклона плоскости к горизонту и сила трения равна:
| Fтр = - µN | (1.83). |
 |  |
| Рисунок - 1.27 | Рисунок - 1.28 |
При малых углах φ тело неподвижно на наклонной плоскости. По мере увеличения угла φ сила F возрастает и при некотором угле φ>φ0 тело скользит по наклонной плоскости. Полагая Р sin φ0 = F0 = µ P cos φ0, найдем связь между коэффициентом статического трения и углом трения:
| µ = tg φ0. | (1.84). |
При действии на соприкасающиеся два тела касательных сил, величина которых меньше предельного значения силы статического трения, тела не проскальзывают друг относительно друга. Если внешняя сила F превзойдет по модулю F0, тело начинает скользить, причем его ускорение определяется результирующей двух сил: внешней F и силы трения скольжения Fтp, величина которой в той или иной мере зависит от скорости скольжения.
В отличие от сухого вязкое трение характерно тем, что сила вязкого трения обращается в нуль одновременно со скоростью. Поэтому, как бы ни была мала внешняя сила, она может сообщить относительную скорость слоям вязкой среды.
Между твердым телом и вязкой (жидкой или газообразной) средой в жидкой или газообразной среде возникают силы сопротивления среды, которые могут быть гораздо значительнее, чем силы трения.. При небольших скоростях эта сила растет линейно со скоростью:
| Fсопр = -rv | (1.85), |
где знак минус означает, что эта сила направлена противоположно скорости. Величина коэффициента r зависит от формы и размеров тела, состояния его поверхности и от свойства среды, называемого вязкостью.
Сила тяжести и вес. Под действием силы притяжения к Земле все тела падают с одинаковым относительно поверхности Земли ускорением g.= 9.81 м/с2. Это означает, что в системе отсчета, связанной с Землей, на всякое тело массы т действует сила, называемая силой тяжести:
| Fтяж = mg | (1.86). |
Когда тело покоится относительно поверхности Земли, сила Fтяж уравновешивается реакцией подвеса или опоры, удерживающего тело от падения (F= - Fтяж). По третьему закону Ньютона тело в этом случае действует на подвес или опору с силой P, равной — Fтяж т. е. с силой
| P = Fтяж = mg | (1.87). |
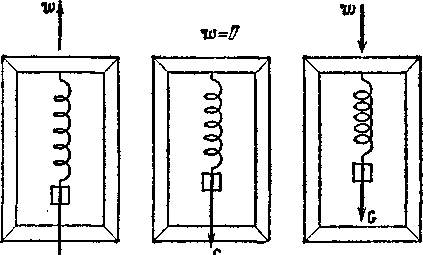
Сила P, с которой тело действует на подвес или опору, называется весом тела. Эта сила равна mg лишь в том случае, когда тело и опора неподвижны относительно Земли (рисунок - 1.29,б). В случае их движения с некоторым ускорением а вес P не будет равен mg. Уравнение движения тела будет иметь вид
| Fтяж + P = mа | (1.88), |
где реакция подвеса представляет собой вес тела Р в этих условиях. Отсюда
| Р =m(g±а) | (1.89). |
Эта формула определяет вес тела в общем случае (в этом предположении выполнены рисунки - 1.29 а,в). В зависимости от направления движения в выражении (1.89) P, обозначим знаком «+» движение, когда а направлен вверх, знак «-» соответствует направлению а вниз. Отсюда следует, что вес Р может быть, как больше, так и меньше силы тяжести Fтяж.. При свободном падении тела с а =g сила Р, с которой тело действует на подвес, равна нулю. Наступает состояние невесомости. Космический корабль, летящий вокруг Земли с выключенными двигателями, движется, как и свободно падающая рамка, с ускорением g, вследствие чего тела внутри корабля находятся в состоянии невесомости — они не оказывают давления на соприкасающиеся с ними тела. Если тело поднимается вверх с а, то наступает явление, которое известно в науке как перегрузка. При этом,
 | ||||
| | а) | б) | в) | |
| Рисунок - 1.29 | ||||
в зависимости от значения а, может быть многократное увеличение собственного веса поднимающегося ввысь тела, что и обозначается как перегрузка.
Отметим, что часто путают силу тяжести Fтяж и вес тела Р. Это обусловлено тем, что в случае неподвижной опоры силы Fтяж и Р совпадают по величине и по направлению (обе они равны mg). Однако следует помнить, что эти силы приложены к разным телам: Fтяж приложена к самому телу, Р приложена к подвесу или опоре, ограничивающим свободное движение тела в поле сил земного тяготения. Кроме того, сила Fтяж всегда постоянна и равна mg, независимо от того, движется тело или покоится. Вес Р зависит величина переменная, зависит от ускорения, с которым движется тело.
1.2.3 Работа сил в механике, энергия. Закон сохранения энергии в механике
Работой постоянной силы F, когда тело движется поступательно и прямолинейно, при прохождении телом пути S, называют величину
| А = FScos α = FτS, | (1.90), |
где α— угол между силой F и направлением движения тела. Здесь. Fτ= Fcos α — проекция силы F на направление вектора v скорости тела (рисунок - 1.30).
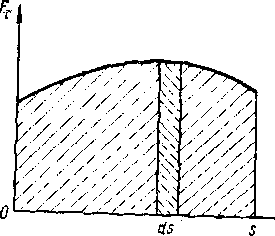
В общем случае тело может двигаться произвольным, достаточно сложным образом, а сила F — изменяться (рисунок - 1.31). Тогда, рассматривая достаточно малое (элементарное) перемещение тела ds, в пределах которой можно считать силу F постоянной, элементарную работу, можно вычислить по формуле:
| dА = Fcosαds = Fτds | (1.91). |
Работа, совершаемая силой F на конечном пути s, равна сумме элементарных работ на отдельных бесконечно малых участках пути; эта сумма приводится к интегралу:
| A = ∫F cos αds = ∫Fτ ds | (1.92). |
Работа, совершаемая силой F на конечном пути S, графически измеряется площадью заштрихованной на рисунке - 1.31 фигурой, ограниченной, с одной стороны функцией F(t), с другой стороны, ординатами, определяемыми S.
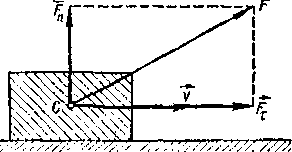 |  |
| Рисунок - 1.30 | Рисунок - 1.31 |
Силу F, действующую на материальную точку, называют консервативной, или потенциальной, если работа А, совершаемая этой силой при перемещении точки из одного произвольного положения в другое, не зависит от того, по какой траектории это перемещение произошло. Поэтому при перемещении материальной точки вдоль замкнутой траектории работа консервативной силы тождественно равна нулю. Таким образом, консервативные силы можно определить двумя способами:
1) как силу, работа которой не зависит от пути, по которому частица переходит из одного положения в другое;
2) как силу, работа которой по замкнутому пути равна нулю.
Примерами консервативных сил могут служить силы всемирного тяготения, силы упругости, силы электростатического взаимодействия между заряженными телами.
Все силы, не удовлетворяющие условию консервативности, называются неконсервативными. Характерным примером таких сил являются силы трения скольжения. Сила трения скольжения всегда направлена в

 сторону, противоположную направлению движения, так что cosα = -1. Поэтому работа силы трения скольжения вдоль замкнутой траектории всегда отрицательна и никогда не равна нулю.
сторону, противоположную направлению движения, так что cosα = -1. Поэтому работа силы трения скольжения вдоль замкнутой траектории всегда отрицательна и никогда не равна нулю.Для характеристики скорости совершения работы силой вводится понятие мощности. Мощностью N силы F называется физическая величина, численно равная работе, совершаемой этой силой за единицу времени:
| N = dA/dt | (1.93. |
Подставляя в эту формулу выражение для элементарной работы, получим
| N = F cosα ds/dt = Fvcosα | (1.94), |
где v — скорость точки приложения силы.
В механике различают два вида энергии, кинетическую и потенциальную. Кинетической энергией тела называют энергию ЕK, являющуюся мерой его механического движения и измеряемую той работой, которую может совершить тело при его торможении до полной остановки. Найдем выражение для кинетической энергии твердого тела В, имеющего массу т и движущегося поступательно со скоростью v.
Пусть тело В тормозится под действием некоторой силой F (в общем случае переменной) и на малом участке пути ds совершает элементарную работу dА = - Fτ ds. По второму закону Ньютона - Fτ= mdv/dt Следовательно, dA = - m (dv/dt) ds = - m (ds/dt) dv = - m v dv. Работа, совершаемая телом В до полной его остановки
| A = - ∫ m v dv = mv2/2 | (1.95). |
Итак, кинетическая энергия поступательно движущегося телa, равна половине произведения массы этого тела на квадрат его скорости:
| Ек = A = mv2/2 | (1.96). |
Данная формула справедлива для кинетической энергии материальной точки. Любую механическую систему можно рассматривать как систему материальных точек. Поэтому кинетическая энергия ЕK механической системы равна сумме кинетических энергий всех п материальных точек, образующих эту систему:
| Ек = ∑ Еi = ∑mivi2/2 | (1.97), |
где mi, vi — масса и скорость i-й материальной точки. Таким образом, кинетическая энергия системы полностью определяется величинами масс и скоростей движения. входящих в нее материальных точек. Она не зависит от того, каким образом части рассматриваемой системы приобрели данные значения скоростей. Кратко этот важный вывод можно сформулировать следующим образом: кинетическая энергия системы есть функция состояния ее движения.
Если на систему материальных точек или тел действуют консервативные (потенциальные) силы, то можно ввести понятие потенциальной энергии этой системы. В самом деле, работа, совершаемая консервативными силами, не зависит от того, как было осуществлено это перемещение. Работа А1-2 при перемещении системы из одной точки пространства, полностью определяется начальной и конечной местоположениями системы. Это можно выразить в форме
| А1-2 = Еп1 – Еп2 | (1.98), |
где Еп — некоторая функция состояния системы, зависящая только от координат всех материальных точек системы. Эту функцию называют потенциальной энергией системы. Отсюда следует, что работа консервативных сил, действующих на механическую систему, равна убыли потенциальной энергии этой системы. Из определения следует, что потенциальная энергия системы в произвольном состоянии равна работе, совершаемой консервативными силами при переводе системы из одного состояния в другое по условию задачи.
Так, например, работа силы тяжести зависит только от разности высот начальной и конечной точек пути. Сила тяжести тела приложена к его центру тяжести. Поэтому работа силы тяжести при любом движении тела равна произведению этой силы на разность высот начального и конечного положений его центра тяжести. Отсюда следует, что работа силы тяжести вдоль замкнутой траектории центра тяжести тела равна нулю, т. е. что сила тяжести, действительно, является консервативной. Потенциальная энергия тела, поднятого на высоту H над поверхностью Земли равна
| En =mgH+ Еno | (1.99), |
где Еn0— потенциальная энергия тела, лежащего на поверхности Земли. Обычно принимают Еn0 = 0, так что
| Еn = mgH. | (1.100). |
Найдем потенциальную энергию упруго деформированного тела. Сила упругости Fynp, как известно из опыта, пропорциональна величине деформации х, т. е. Fynp, = - kх где k — коэффициент упругости, характеризующий упругие свойства тела, а знак минус показывает, что сила упругости направлена в сторону, противоположную направлению деформации: упруго деформированное тело стремится восстановить свои первоначальные форму и размеры.
Элементарная работа, совершаемая силой Fynp при бесконечно малом изменении деформации тела на величину dx равна dА = (Fynpdx) = - kxdx. Работа этой силы при конечном изменении деформации тела, например, при переводе его из недеформированного состояния (х=0) в состояние, соответствующее деформации х, равна
| А = - ∫kxdx = - kx2/2 | (1.101). |
Работа А не зависит от хода процесса деформации тела и полностью определяется значениями деформации тела в начальном и конечном состояниях. Следовательно, силы упругости являются консервативными, а потенциальная энергия упруго деформированного тела
| Еn = kx2/2. | (1.102). |
Полной механической энергией системы называют величину E, равную сумме кинетической и потенциальной энергий этой системы:
| E = EK+ En. | (1.103). |
Полная механическая энергия системы — функция ее состояния, так как зависит только от координат, скоростей и масс всех малых частей (материальных точек) системы
Найдем условие, которому должна удовлетворять система тел для того, чтобы ее полная механическая энергия не изменялась с течением времени. Если v — скорость i-й материальной точки с массой ти то ее кинетическая энергия Eкi = mivi2/2. Изменение этой энергии за малый промежуток времени dt, связанное с изменением скорости v, на dvi= aidt (аi— ускорение рассматриваемой материальной точки), равно
| dEкi = mi /2[(dvi, vi) + (vi ,dvi,)] = mi(aidt, vi,) = (miаi, vtdt) = (miаi, dri) | (1.104), |
где dri = vidt— приращение радиуса-вектора ri, материальной точки. По второму закону Ньютона miаi = Fi + fi, где Fi и fi — результирующие, соответственно, консервативных и неконсервативных сил, действующих на i-ю материальную точку. Поэтому
| dEкi. = (Fi dri) + (fi dri) | (1.105). |
Кинетическая энергия WK всей системы равна сумме кинетических энергий всех п материальных точек, образующих эту систему, а ее изменение за малый промежуток времени dt dЕк = ∑dEкi., т. е.
| dЕк =∑(Fi dri) +∑(fi dri) | (1.106). |
Первая сумма в правой части этого уравнения представляет собой суммарную работу dA, совершаемую всеми консервативными силами за промежуток времени dt. Эта работа равна убыли за то же время dt потенциальной энергии системы
| Еn = Еnвнутр + Еnвнешн | (1.107), |
| ∑(Fi dri) = dA = - dЕn | (1.108). |
Вторая сумма в правой части уравнения ∑(fi dri).представляет собой суммарную работу dAнк, совершаемую всеми неконсервативными силами. Таким образом, уравнение можно переписать в форме dЕк + dЕn = dAнк, или
| dЕ = dAнк, | (1.109), |
где Е= Е K+ Е n — полная механическая энергия системы.
Если внутренние силы взаимодействия между которыми консервативны, а все внешние силы — стационарны и консервативны, такую систему тел (материальных точек) называют консервативной системой,. Для такой системы dA = dE = 0 и
| E = EK+ Eп= const, | (1.110), |
т. е. полная механическая энергия консервативной системы не изменяется с течением времени. Этот закон называют законом сохранения механической энергии. Он справедлив, для замкнутой консервативной системы, т е системы, на которую внешние силы не действуют, а все внутренние силы — консервативны.
Рассмотрим применение закона сохранения механической энергии к расчету абсолютно упругого прямого центрального удара двух тел. Абсолютно упругим называют такой удар, в результате которого не происходит превращения механической энергии системы соударяющихся тел в другие виды энергии. Пусть два абсолютно упругих шара с массами m1 и m2 до удара (рисунок - 1.32, а) движутся поступательно со скоростями v1 и v2, направленными в одну и ту же сторону вдоль линии их центров, причем v1 > v2. Нужно найти скорости шаров u1 и u2 после соударения (рисунок - 1.32, б).
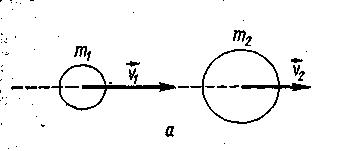 | 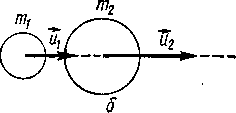 |
| Рисунок - 1.32 | |
В процессе удара систему соударяющихся тел можно считать замкнутой. Следовательно, для решения этой задачи можно воспользоваться законами сохранения механической энергии и импульса. Перед ударом и после его завершения соударяющиеся тела не деформированы, т. е. потенциальную энергию системы в этих двух состояниях можно считать одинаковой и равной нулю. Тогда из закона сохранения механической энергии имеем
| m1v12/2 + m2v22/2 = m1u12/2 + m2u22/2 | (1.111), |
где u1 и u2 скорости этих шаров после соударения. По закону сохранения импульса
| m1v1 + m2v2 = m1u1 + m2u2 | (1.112). |
Совместное решение двух последних уравнений дает
| u1 = [v1(m1-m2)+ 2m2v2] / (m1+m2), u2 = [v2(m2-m1)+ 2m1v1] / (m1+m2) | (1.113), |
т.е., после упругого соударения тела двигаются каждая со своей скоростью кинетической энергией Е1 и Е2 соответственно.
Систему тел называют диссипативной, если ее механическая энергия постепенно уменьшается за счет преобразования в другие (немеханические) формы энергии. Этот процесс называют процессом диссипации (рассеяния) энергии. В качестве примера рассмотрим диссипацию энергии при абсолютно неупругом прямом центральном ударе двух поступательно движущихся тел.
При абсолютно неупругом ударе происходит диссипация энергии. Изменение ∆E полной механической энергии системы соударяющихся тел равно изменению их кинетической энергии
| ∆E = ∆Eк =(m1+m2)u2/2 - [m1v12/2 + m2v22/2] | (1.114). |
Общую скорость тел можем найти, применяя закон сохранения импульса для неупругого удара, учитывая, что после соударения они двигаются вместе, имея общую скорость:
| u = (m1v1 + m2v2)/ (m1+m2) | (1.115. |
После преобразований, рассеянная энергия равна:
| ∆E =- m1m2 (v1 –v2)2 /2(m1+m2) | (1.116). |
1.3 Динамика вращательного движения твердых тел
1.3.1 Момент силы, момент импульса. Закон сохранения момента импульса
В механике твердым телом называется совокупность материальных частиц, взаимное расположение которых остается неизменным. Основные законы механики определяют движение отдельной материальной точки.
При вращательном движении угловая скорость и угловое ускорение одинаковы в каждый данный момент для всех частиц тела. В связи с неизменностью взаимного расположения частиц линейные скорости и линейные ускорения пропорциональны расстоянию частиц от оси вращения. Этим определяется та исключительная роль, которую играет расстояние частиц от оси вращения в динамике вращательных движений твердого тела.
Если на твердое тело, имеющее закрепленную ось вращения, действует сила F, приложенная в точке А (рис. 54), то очевидно, что составляющая F1 этой силы, параллельная оси вращения, никакого вращательного эффекта дать не может, и только другая составляющая, лежащая в плоскости, перпендикулярной к оси вращения, F2, дает вращательный эффект, который тем более значителен, чем больше кратчайшее расстояние между прямой, по которой действует сила, и осью вращения.
Поэтому моментом силы относительно оси называют произведение проекции силы (на плоскость, перпендикулярную к оси) и кратчайшего расстояния между прямой, по которой действует сила, и осью. Момент силы относительно оси рассматривают как вектор, направленный по оси туда, куда нужно смотреть, чтобы видеть силу обращенной в сторону движения часовой стрелки (т. е. на рисунке - 1.33 вниз). Момент силы F относительно оси численно равен М = F2p.
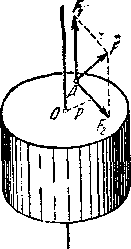 |
| Рисунок - 1.33 |
Твердое тело можно мысленно представить в виде системы материальных точек — достаточно малых частей этих тел. Рассмотрим произвольную механическую систему, состоящую из п материальных точек. Пусть mi— масса i-й точки системы, а ri— радиус-вектор, проведенный в эту точку из начала координат О неподвижной инерциальной системы отсчета.
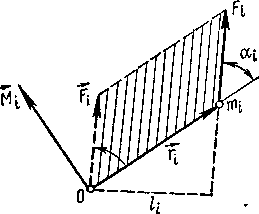
Векторное произведение радиуса-вектора ri, проведенного в точку приложения силы Fi на' эту силу называют моментом М силы, Fi относительно точки О:
| Мi = [ri Fi] | (1.117). |
Векторы Мi , ri и Fi образуют правую тройку (рисунок - 1.34). Численное значение момента силы F; равно
| Мi = Fi risinα = Fili | (1.118, |
где α-— угол между векторами ri и Fi, risinα = li— длина перпендикуляра, опущенного из точки О на линию действия силы Ft. Величина lt называется плечом силы Fi. Если линия действия силы проходит через точку О, то lt = 0 и момент силы относительно точки О тоже равен нулю.
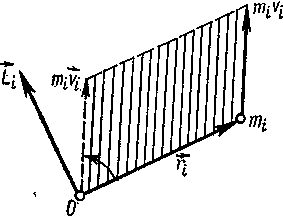
Векторное произведение радиуса-вектора ri на ее импульс mv, называют моментом импульса Li относительно точки О:
| Li = [rimivi] | (1.119). |
Он направлен перпендикулярно к плоскости, проведенной через векторы ri и mivi и образует с ними правую тройку векторов: при наблюдении из конца Li видно, что кратчайший поворот от ri к mivi происходит против часовой стрелки (рисунок - 1.35). Из полученных соотношений следует, что скорость изменения момента импульса Li i-ой материальной точки равна
| dL/dt = ∑Mik + Miвнешн | (1.120). |
Сложим почленно все уравнения, записанные для каждой из n материальных точек системы: ∑dLi/dt =∑ ∑Mik + ∑Miвнешн. Векторную сумму моментов Miвнешн всех внешних сил, приложенных ко всем материальным точкам системы, называют результирующим, или главным моментом М внешних сил относительно точки О: М = ∑Miвнешн
 |  |
| Рисунок - 1.34 | Рисунок - 1.35 |
Векторную сумму моментов импульса Li, всех материальных точек системы называют моментом импульса (количества движения) L тела относительно точки О:
| L = ∑Li =∑[ri,mivi] | (1.121). |
Для тела выполняется соотношение:
| dL/dt =∑dLi/dt | (1.122). |
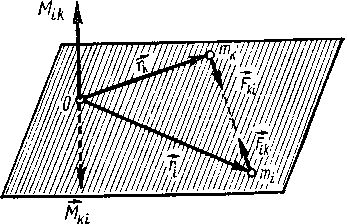
Наконец, векторная сумма моментов всех внутренних сил Flk взаимодействия между всеми точками системы относительно точки 0 равна нулю: ∑ ∑Mik = 0. Это связано с тем, что по третьему закону Ньютона силы F iк и Fkt численно равны, имеют общую линию действия, но направлены во взаимно противоположные стороны. Поэтому их моменты Mik = [ri, Fik] и Mki = [rk,, Fki] относительно точки О, численно равны и противоположны по направлению (рисунок - 1.36).
 |
| Рисунок - 1.36 |
Поэтому
| ∑dL/dt = M | (1.123). |
Таким образом, скорость изменения момента импульса системы относительно неподвижной точки равна результирующему моменту относительно той же точки всех внешних сил, действующих на систему. Это утверждение выражает основной закон динамики для тела, вращающегося вокруг неподвижной точки. Отсюда следует, что момент импульса L является основной динамической характеристикой тела, вращающегося вокруг неподвижной точки.
Из основного закона динамики для тела, вращающегося вокруг неподвижной оси, следует закон сохранения момента импульса тела относительно этой оси: если момент внешних сил относительно неподвижной оси вращения тела тождественно равен нулю, то момент импульса тела относительно этой оси не изменяется. Действительно для случая, когда на тело либо вовсе не действуют внешние силы, либо они таковы, что их равнодействующая не дает момента относительно оси вращения. Тогда dL = M dt = 0. Но если dL равно нулю, то, следовательно, сама величина момента импульса L = остается постоянной: L = const. Этот утверждение и носит название закона сохранения момента импульса относительно оси вращения.
Закон сохранения момента импульса, подобно законам сохранения импульса и энергии, является одним из фундаментальных законов природы. В теоретической физике доказано, что этот закон — следствие изотропности пространства. Изотропность пространства означает, что при повороте в нем замкнутой системы как целого (иначе говоря, при изменении ориентации осей координат) физические свойства замкнутой системы и законы ее движения не изменяются.
1.3.2 Кинетическая энергия вращательного движения. Момент инерции
Кинетическая энергия вращающегося тела равна сумме кинетических энергий всех частиц тела:
| Eк = ∑mivi2/2 | (1.124), |
где тi-— масса какой-либо частицы, а vi— ее линейная скорость, пропорциональная расстоянию ri данной частицы от оси вращения. Подставляя в это выражение vi= ωri и вынося за знак суммы общую для всех частиц угловую скорость ω, находим:
| Eк = ω2/2∑miri2 | (1.125). |
Эту формулу для кинетической энергии вращающегося тела можно привести к виду, аналогичному выражению кинетической энергии поступательного движения, если ввести величину момента инерции тела. Моментом инерции материальной точки называют произведение массы точки на квадрат расстояния от оси вращения:
| Ii = miri2 | (1.126). |
С использованием понятия момента инерции кинетическая энергия вращающегося тела определяется такой формулой:
| Е = Iω2/2 | (1.127). |
Сравнивая формулы кинетической энергии тела при поступательном и вращательном движении, находим, что роль массы тела во вращательном движении играет момент инерции I. Отсюда следует, что момент инерции играет ту же роль, что и масса для поступательного движения, как меры инертности.
Зная формулу момента инерции материальной точки, можно вычислить момента инерции любого тела. Для того необходимо дифференцировать тело на такие маленькие кусочки dm, когда их можно принять материальной точкой: это позволяет применить к ним соответствующую формулу dIi = ri2dm. Тогда момент инерции тела можно вычислить как сумму моментов инерции всех точек, образующих это тело:I = ∑miri2. Или, учитывая, что тело является сплошной средой, математически можно вычислить через интеграл:
| I = ∫miri2 | (1.128). |
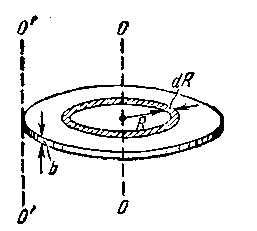
В качестве примера найдем момент инерции однородного диска относительно оси, перпендикулярной к плоскости диска и проходящей через его центр (рисунок - 1.37). Разобьем диск на кольцевые слои толщиной dR. Все точки одного слоя будут находиться на одинаковом расстоянии от оси, равном R. Объем такого слоя равен dV=b2πRdR, где b — толщина диска. Поскольку диск однороден, плотность его во всех точках одинакова и ρ в уравнении можно вынести за знак интеграла: I = ρ∫R2dV = ρ∫R2b2nRdR, где R— радиус диска. Вынесем за знак интеграла постоянный множитель 2πb: I=2πbρ∫ R2 dR = 2πbρ R4/4. Наконец, введя массу диска т, равную произведению плотности р на объем диска bπR2, получим:
| I = mR2/2 | (1.129). |
 |
| Рисунок - 1.37 |
Если необходимо найти момент инерции диска относительно, любой оси например, оси О'О' (рисунок - 1.37), вычисления оказываются более сложными. Нахождение момента инерции значительно облегчается, если воспользоваться теоремой Штейнера: момент инерции I относительно произвольной оси равен сумме момента инерции Ic относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела т на квадрат расстояния а между осями:
| 1 = 1с + та2 | (1.130). |
Теорема Штейнера сводит вычисление момента инерции относительно любой произвольной оси к вычислению момента инерции относительно оси, проходящей через центр масс тела. Ниже приводятся моменты инерции некоторых однородных тел простейшей формы (таблица - 1.1). Полученные данные показывают, что момент инерции тела зависит не только от его массы, но и от ее распределения относительно оси вращения.
Таблица - 1.1 Моменты инерции некоторых тел
| Тело | Положение оси О | Момент инерции |
| Полый тонкостенный цилиндр радиуса R, массой m | Ось симметрии | Jо = mR2 |
| Сплошной цилиндр (или диск) радиуса R, массой m | Ось симметрии | Jо = mR2/2 |
| Прямой тонкий стержень, длиной l и массой m | Ось перпендикулярна к стержню и проходит через его середину | Jо = ml2/12 |
| Тот же стержень | Ось перпендикулярна к стержню и проходит через его конец | Jо = ml2/3 |
| Шар радиуса R, массой m | Ось проходит через центр шара | Jо = 2mR2/5 |
