Т. С. Рамазанов доктор физико-математических наук, профессор, Казну им. Аль-Фараби, г. Алматы; > С. К. Тлеукенов доктор физико-математических наук, профессор, пгу им. С. Торайгырова, г. Павлодар; > А. М. Мубараков
| Вид материала | Учебник |
- Титульный лист программы Форма обучения по дисциплине ф со пгу 18. 3/37 (Syllabus), 349.17kb.
- Б. А. – доктор юридических наук, профессор Казну им аль-Фараби, 209.21kb.
- Карпухин В. Б., доктор физико-математических наук, профессор кафедры «Высшая и прикладная, 263.95kb.
- А. М. Мубараков доктор пед наук, профессор. Н. Э. Пфейфер доктор пед наук, профессор, 1066.25kb.
- Веселаго Виктор Георгиевич, доктор физико-математических наук, профессор мфти, область, 30.58kb.
- Практических: 0 Лабораторных, 16.69kb.
- Практических: 34 Лабораторных, 24.5kb.
- Практических: 0 Лабораторных, 16.63kb.
- Практических: 34 Лабораторных, 20.05kb.
- Практических: 0 Лабораторных, 18.53kb.
I Механика
1.1 Кинематика материальной точки
1.1.1 Понятие материальной точки. Система отсчета. Траектория, путь, перемещение Единицы измерения
Механика – часть физики, которая изучает закономерности механического движения. Для установления связей и отношений, которые имеют место в том или ином процессе, необходимо произвести измерения. Для этого нужно выбрать эталон данной физической величины и установить способ сравнения этих физических величин. Для построения системы единиц произвольно выбирают единицы для нескольких не зависящих друг от друга физических величин. Эти единицы называются основными. Основные единицы измерения имеют специальные эталоны измерения, которые, и хранятся в особых условиях. Остальные же величины и их единицы выводятся из законов, связывающих эти величины с основными единицами измерений. Они называются производными. Построенные по этому принципу системы единиц носят название абсолютных. Существует несколько систем единиц, отличающихся выбором тех величин, которые приняты за основные и для которых установлены специальные эталоны.
В настоящее время в физике согласно Государственному стандарту (ГОСТ 8.417—81), обязательна к применению Система Интернациональная (СИ), которая строится на семи основных единицах — метр, килограмм, секунда, ампер, кельвин, моль, кандела — и двух дополнительных — радиан и стерадиан.
Метр (м) —длина пути, проходимого светом в вакууме за 1/299 792 458 с.
Килограмм (кг) — масса, равная массе международного прототипа килограмма (платиноиридиевого цилиндра, хранящегося в Международном бюро мер и весов в Севре, близ Парижа).
Секунда (с) — время, равное 9 192 631 770 периодам излучения, соответствующего переходу между двумя сверхтонкими уровнями основного состояния атома цезия-133.
Ампер (А) — сила постоянного тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малого поперечного сечения, расположенным в вакууме на расстоянии 1 м один от другого, создает между этими проводниками силу, равную 2-10-7Н на каждый метр длины.
Кельвин (К) — 1/273,16 часть термодинамической температуры тройной точки воды.
Моль (моль) — количество вещества системы, содержащей столько же структурных элементов, сколько атомов содержится в нуклиде 12С массой 0,012 кг.
Кандела (кд) — сила света в заданном направлении источника, испускающего монохроматическое излучение частотой 540•1012 Гц, энергетическая сила света которого в этом направлении составляет 1/683 Вт/ср.
Радиан (рад) — угол между двумя радиусами окружности, длина дуги между которыми равна радиусу.
Стерадиан (ср) — телесный угол с вершиной в центре сферы, вырезающий на поверхности сферы площадь, равную площади квадрата со стороной, равной радиусу сферы.
С помощью основных величин можно получить другие величины либо используя выражения для законов природы, либо путем целесообразного определения через умножение или деление основных величин. Например, Скорость = Путь/Время, Работа = Сила • Путь, Плотность = Масса/Объем, Заряд = Сила тока • Время, и т. д. При этом необходимо соблюдать правило размерности.
Размерность физической величины есть ее выражение в основных единицах. Размерности обеих частей физических равенств должны быть одинаковыми, так как физические законы не могут зависеть от выбора единиц физических величин. Поэтому можно проверять с помощью размерности правильность полученных физических формул.
Для представления физических величин, особенно в формулах, таблицах или на графиках, используются специальные символы — обозначения величин. В согласии с международными соглашениями. Единицы Международной системы (СИ) при практическом использовании часто оказываются слишком большими или слишком малыми, поэтому с помощью особых приставок могут быть образованы десятичные кратные и дольные единицы, если это не запрещено в отдельных случаях. Сводка этих приставок дана в специальных справочных таблицах. Существуют некоторые правила использования приставок. Приведем важнейшие из них:
а) единица измерения не может содержать более одной приставки.
б) комбинация сокращенного обозначения приставки и единицы измерения составляют единый символ.
Например, для измерения давления, допускается – исторически сложившееся единица измерения – мм.рт. столба, или, так как Фарад – очень крупная единица измерения, в повседневной жизни можно выражать емкость конденсатора долями Фарад: пФ, мФ и т.д. Но при расчетах необходимо придерживаться определенной системы, производить все расчеты в одной системе, предпочтительно в СИ.
Главной задачей механики является характеристика движения тела в пространстве с течением времени. Механическое движение – это изменение с течением времени взаимного расположения тел или их частей в пространстве. Чтобы описать механическое движение применяют ряд научных абстракций, который позволяет отразить закономерности того или иного вида движения.
Движущееся тело обладает определенными размерами — протяженностью в пространстве. Иногда форма и размер тела не влияют на само движение и все процессы в ней. Тогда можно абстрагироваться от несущественного, незначительного, в условиях данной задачи, и рассматривать ее как геометрическую точку, приписав ей массу физического тела. Такая абстракция называется материальной точкой. Следует указать, что вообще, вводя абстрактные понятия, в науке отвлекаются от всех свойств тел, несущественных для рассматриваемого явления, упрощая, таким образом, задачу и концентрируя внимание на тех свойствах тел, которые предопределяют характер изучаемого явления. Материальной точкой называется тело, размеры которого пренебрежимо малы по сравнению с масштабами движения.
Изучая более подробно внутренние свойства конкретных тел, мы можем прийти к понятию твердого тела как системы жестко связанных между собой материальных точек упругого тела, как системы точек, способных к небольшим относительным смещениям. С помощью таких абстракций можно изучить, например, давление газа на стенки сосуда, в котором он заключен.
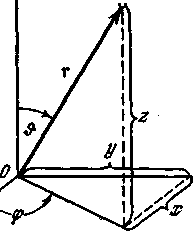
Определять положение точки «по отношению к пустому пространству» невозможно и физически бессмысленно. Можно определять положение любого тела, в том числе и материальной точки, лишь по отношению к другому, произвольно выбранному материальному телу, называемому телом отсчета. Выбранное таким образом тело условно считается неподвижным. Связывая с этим телом произвольную систему координат, мы получим систему отсчета положений материальной точки. Для задания положения этого тела в пространстве система координат, которая будет каждый раз показывать ее местоположение в тот или иной момент времени общепринята трехмерная, простейшая декартовая прямоугольная система координат (рисунок - 1.1). Положение точки М в этой системе характеризуется тремя координатами: х — абсцисса, у — ордината и z — аппликата точки: М{х, у, z). Они являются проекциями радиуса-вектора ОМ=r, проведенного из начала координат в точку М(r).
Вместо координат х, у, z, радиус-вектор r может характеризовать положение точки в пространстве, задавая, например, его длину /r/ и два угла: θ, между радиусом-вектором r и осью 0Z и φ между проекцией r на плоскость XY и осью ОХ, как это показано на чертеже. Такая система описания движения называется сферической системой координат.
Во всех случаях, радиус-вектор r и положение точки в пространстве характеризуются количественно тремя числами, которые могут меняться независимо друг от друга. Это является математическим отражением того факта, что пространство трехмерно. Поскольку три величины, характеризующие положение точки в пространстве, взаимно независимы, говорят, что материальная точка обладает тремя степенями свободы, которые описывают положение материальной точки или твердого тела в любой момент времени и называются законами движения. Такие уравнения называют кинематическими уравнениями движения. Для измерения хода времени, в течение которого происходило движение, необходим счетчик времени, который также входит, как обязательный для описания движения, элемент в систему отсчета.
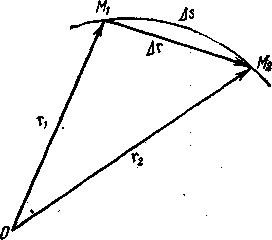
Совокупность последовательных положений, занимаемых точкой М в процессе ее движения, образует в пространстве линию, называемую траекторией движущейся точки. На рисунке - 1.2 изображен отрезок траектории.
 |  |
| Рисунок - 1.1 | Рисунок - 1.2 |
В какой-то момент времени t1 точка М занимает на траектории положение М1, характеризуемое радиус-вектором ОМ1 = r1. Если материальная точка движется, то ее положение в пространстве с течением времени меняется:
| r = r(t) | (1.1) |
либо
| x = x(t), y = y(t), z = z(t) | (1.2) |
M1M2 = S при этом представляет собой путь, пройденный точкой М за время ∆t
 . Вектор M1M2=∆r, проведенный из начального положения М1 в конечное положение М2, называется вектором перемещения точки М за время ∆t. При прямолинейном движении |∆r| = ∆s. В общем случае, как это видно из рисунка, |∆r| ≠∆s, но различие между ними тем меньше, чем меньше ∆r. Очевидно, что при произвольном криволинейном движении равенство |∆r|=∆s соблюдается лишь в пределе для бесконечно малого промежутка времени, т. е. когда ∆r →0:lim∆s/|∆r| = 1.Из рис. 1.2 видно, чтоr2 = r1 + |∆r|, или
. Вектор M1M2=∆r, проведенный из начального положения М1 в конечное положение М2, называется вектором перемещения точки М за время ∆t. При прямолинейном движении |∆r| = ∆s. В общем случае, как это видно из рисунка, |∆r| ≠∆s, но различие между ними тем меньше, чем меньше ∆r. Очевидно, что при произвольном криволинейном движении равенство |∆r|=∆s соблюдается лишь в пределе для бесконечно малого промежутка времени, т. е. когда ∆r →0:lim∆s/|∆r| = 1.Из рис. 1.2 видно, чтоr2 = r1 + |∆r|, или| ∆r = r2-rl | (1.3) |
т. е. вектор перемещения равен геометрической разности радиусов-векторов конечного и начального положения точки; этот вектор представляет собой приращение радиуса-вектора и характеризует изменение положения точки М в пространстве за время ∆t.
