Т. С. Рамазанов доктор физико-математических наук, профессор, Казну им. Аль-Фараби, г. Алматы; > С. К. Тлеукенов доктор физико-математических наук, профессор, пгу им. С. Торайгырова, г. Павлодар; > А. М. Мубараков

Вид материала

Учебник

Содержание 1.1.3 Кинематика прямолинейного движения

Подобный материал:

• Титульный лист программы Форма обучения по дисциплине ф со пгу 18. 3/37 (Syllabus), 349.17kb.
• Б. А. – доктор юридических наук, профессор Казну им аль-Фараби, 209.21kb.
• Карпухин В. Б., доктор физико-математических наук, профессор кафедры «Высшая и прикладная, 263.95kb.
• А. М. Мубараков доктор пед наук, профессор. Н. Э. Пфейфер доктор пед наук, профессор, 1066.25kb.
• Веселаго Виктор Георгиевич, доктор физико-математических наук, профессор мфти, область, 30.58kb.
• Практических: 0 Лабораторных, 16.69kb.
• Практических: 34 Лабораторных, 24.5kb.
• Практических: 0 Лабораторных, 16.63kb.
• Практических: 34 Лабораторных, 20.05kb.
• Практических: 0 Лабораторных, 18.53kb.

1.1.3 Кинематика прямолинейного движения

Равномерное прямолинейное движение. Равномерным прямолинейным называют такое движение, которое происходит по прямолинейной траектории, и когда за любые равные промежутки времени тело совершает одинаковые перемещения. Скоростью равномерного прямолинейного движения называют векторную величину, равную отношению перемещения тела к промежутку времени, в течение которого было совершено это перемещение: v=r/t

Направление скорости в прямолинейном движении совпадает с направлением перемещения, поэтому модуль перемещения равняется пути движения: /r/ = S. Поскольку в равномерном прямолинейном движении за любые равные промежутки времени тело совершает равные перемещения, скорость такого движения является величиной постоянной (v= const):

v = S/t

(1.16).

Это выражение называется уравнением скорости равномерного прямолинейного движения, откуда следует уравнением пути равномерного прямолинейного движения:

S = vt

(1.17).

Это движение можно графически отобразить в разных координатах. В системе v(t), равномерное прямолинейное движение скорость будет представлять собой прямую, параллельную оси абсцисс, а путь – площадь четырехугольника со сторонами равными величине постоянной скорости и времени, в течение которой происходило движение (рисунок - 1.8). В координатах S(t), путь отражается наклонной прямой, а о скорости можно судить по тангенсу угла наклона этой прямой (рисунок - 1.9) Пусть ось Ох системы координат, связанный с телом отсчета, совпадает с прямой, вдоль которой движется тело, а x₀ является координатой начальной точки движения тела.

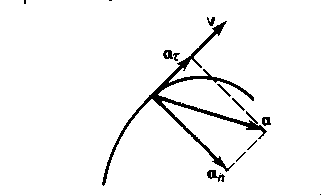Рисунок - 1.7	Рисунок - 1.8

Вдоль оси Ох направлены и перемещение S, и скорость v движущегося тела. Теперь можно установить кинематический закон равномерного прямолинейного движения, т. е. найти выражение для координаты движущегося тела в любой момент времени.

x = x0+vxt

(1.18).

По этой формуле, зная координату х₀ начальной точки движения тела и скорость тела v (ее проекцию v_x на ось Ох), в любой момент времени можно определить положение движущегося тела. Правая часть формулы является алгебраической суммой, так как и х₀, и v_x могут быть и положительными, и отрицательными (ее графическое представление дано на рисунке- 1.10).

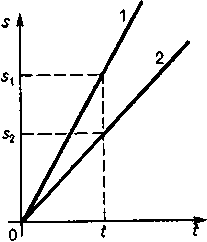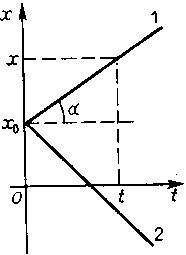Рисунок - 1.9	Рисунок - 1.10

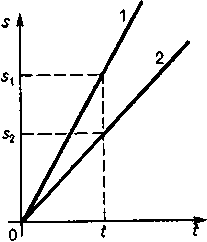
Прямолинейное движение, при котором скорость тела за любые равные промежутки времени изменяется одинаково, называют равнопеременным прямолинейным движением. Быстроту изменения скорости характеризуют величиной, обозначаемой а и называемой ускорением. Ускорением называют векторную величину, равную отношению изменения скорости тела (v - v₀) к промежутку времени t, в течение которого это изменение произошло: a=(v-v₀)/t. Здесь v₀ — начальная скорость тела, v — мгновенная скорость тела в рассматриваемый момент времени.

Прямолинейное равнопеременное движение есть движение с постоянным ускорением (a = const). В прямолинейном равноускоренном движении векторы v₀, v и а направлены по одной прямой. Поэтому модули их проекций на эту прямую равны модулям самих этих векторов.

Найдем кинематический закон прямолинейного равноускоренного движения. После преобразования получим уравнение скорости равноускоренного движения:

v = v0 +at

(1.19).

Уравнение пути равноускоренного движения будет

S= v0t + at2/2.

(1.20).

Если рассматривать два последних уравнения как систему уравнений и исключить параметр t, то получим еще одно соотношение для равнопеременного движения:

(v2 - v02) = 2аS

(1.21).

Если первоначально тело покоилось (v0 ==0),

v =√ 2аS

(1.22).

Графики скорости прямолинейного равноускоренного движения изображены на рисунке – 1.11. На этом рисунке графики 1 и 2 соответствуют движению с положительной проекцией ускорения на ось Ох (скорость увеличивается), а график 3 соответствует движению с отрицательной проекцией ускорения (скорость уменьшается). График 2 соответствует движению без начальной скорости, а графики 1 и 3 — движению с начальной скоростью v_0x. Угол наклона графика к оси абсцисс зависит от ускорения движения тела. Для построения зависимости координаты от времени (график движения) на оси абсцисс откладывают время движения, а на оси ординат — координату движущегося тела.

Пусть тело движется равноускоренно в положительном направлении Ох выбранной системы координат. Тогда уравнение движения тела имеет вид:

х = х0 + v oxt

(1.23).

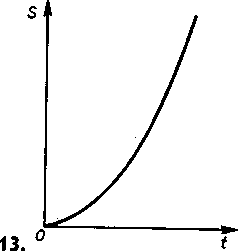
Графиком этой зависимости является парабола, ветви которой направлены вверх, если а>0, или вниз, если а<0. Чтобы построить график пути, на оси абсцисс откладывают время, а на оси ординат - длину пути, пройденного телом. В равноускоренном прямолинейном движении зависимость пути от времени выражается формулами, которые отражают квадратичную зависимость. Следовательно, графиком пути прямолинейного равнопеременного движения является ветвь параболы (рисунок - 1.12).

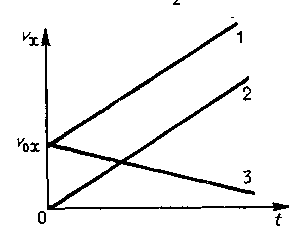Рисунок - 1.11	Рисунок - 1.12