Т. С. Рамазанов доктор физико-математических наук, профессор, Казну им. Аль-Фараби, г. Алматы; > С. К. Тлеукенов доктор физико-математических наук, профессор, пгу им. С. Торайгырова, г. Павлодар; > А. М. Мубараков

Вид материала

Учебник

Содержание 1.1.4 Движение точки по окружности. Связь между линейными и угловыми кинематическими параметрами R этой окружности за время Δt Угловым ускорением R = const. Поэтому вращательное движение можно характеризовать и линейными параметрами: линейной скоростью v R, линейная скорость v = dS/dt

Подобный материал:

• Титульный лист программы Форма обучения по дисциплине ф со пгу 18. 3/37 (Syllabus), 349.17kb.
• Б. А. – доктор юридических наук, профессор Казну им аль-Фараби, 209.21kb.
• Карпухин В. Б., доктор физико-математических наук, профессор кафедры «Высшая и прикладная, 263.95kb.
• А. М. Мубараков доктор пед наук, профессор. Н. Э. Пфейфер доктор пед наук, профессор, 1066.25kb.
• Веселаго Виктор Георгиевич, доктор физико-математических наук, профессор мфти, область, 30.58kb.
• Практических: 0 Лабораторных, 16.69kb.
• Практических: 34 Лабораторных, 24.5kb.
• Практических: 0 Лабораторных, 16.63kb.
• Практических: 34 Лабораторных, 20.05kb.
• Практических: 0 Лабораторных, 18.53kb.

1.1.4 Движение точки по окружности. Связь между линейными и угловыми кинематическими параметрами

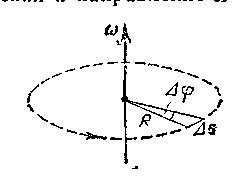
Вращательным называется движение точки, траекторией которой является окружность. Пусть радиус R этой окружности за время Δt поворачиваются на угол Δφ. Этот угол Δφ - называется угловым перемещением точки (рисунок - 1.13).

Угловой скоростью ω называется предел, к которому стремится отношение углового перемещения Δφ к промежутку времени Δt, за который это перемещение произошло, при бесконечном убывании Δt, т. е.

ω =lim Δφ/Δt = dφ/dt

(1.24).

Угловым ускорением называется предел отношения изменения угловой скорости Δω за промежуток времени Δt при бесконечном уменьшении последнего, т. е.

ε = lim Δω/Δt = dω/dt.

(1.25).

Вращательное движение можно представить как частный случай криволинейного движения с постоянным радиусом кривизны: R = const. Поэтому вращательное движение можно характеризовать и линейными параметрами: линейной скоростью v, линейным ускорением a{a_n,a_τ}. Между линейной и угловой характеристиками существует связь, которая позволяет, в зависимости от условия задачи, легко переходить от одних параметров описания к другим.

Для точки, движущейся по окружности радиуса R, линейная скорость v = dS/dt, где dS — путь, пройденный телом по дуге окружности за промежуток времени dt:dS= Rdφ. Подставив ее в формулу линейной скорости, получим

v = ωR.

(1.26).

Данная формула выражает связь между линейной и угловой скоростями движения точки по окружности. Криволинейное движение точки описывается нормальным ускорением a_n. Произведя с ней некоторые преобразования, получим:

an = v2/R =(ωR)2/R =ω2R

(1.27).

Тангенциальное ускорение связано с угловым ускорением следующим образом:

aτ = dv/dt = d(ωR)/dt = R•dω/dt = ε•R.

(1.28).

Угловая скорость и угловое ускорение – вектора. Поэтому необходимо уточнить, как они ориентированы в пространстве. Для этого требуется задать ось вращения и указать, в какую сторону происходит вращение. Можно связать направление угловой скорости с движением буравчика: угловой скорости приписывают то направление, в котором будет двигаться (ввинчиваться или вывинчиваться) буравчик, если его вращать в направлении изображаемого вращения (рисунок - 1.14).

Угловая скорость обладает всеми свойствами векторных величин и

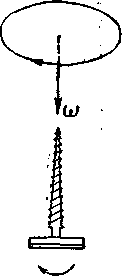Рисунок - 1.13	Рисунок - 1.14

поэтому можно к нему применить правило векторного произведения, которая связывает три вектора следующим образом:

v = [ωR].

(1.29).

Они связаны между собой правилом правого винта: вращение от ω к R покажет направление поступательного движения тела (v) в данный момент времени. Если направление оси вращения остаётся неизменным, то вектор ε лежит на той же оси, что и вектор угловой скорости. Он совпадает по направлению с ω, если угловая скорость возрастает по величине (рисунок - 1.15,а), и направлен в противоположную сторону, если ω уменьшается (рисунок - 1.15,в).

Промежуток времени, в течение которого материальная точка, двигаясь по окружности, совершает один полный оборот, называют периодом обращения. Период обращения обозначают буквой Т и выражают в секундах. Величину п, обратную периоду обращения и равную числу оборотов, совершаемых телом за единичное время, называют частотой обращения - n =1/T.

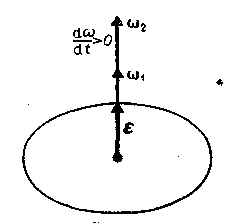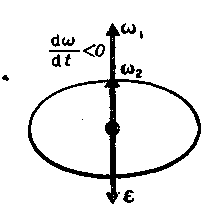а)	в)
Рисунок - 1.15