Карпухин В. Б., доктор физико-математических наук, профессор кафедры «Высшая и прикладная математика» Учебно-методический комплекс по дисциплине «Теория массового обслуживания» составлен в соответствии с требованиями Государственного образовательного стандарта высшего профессионального образования п

Вид материала

Содержание

1. Цель изучения дисциплины
2. Требования к уровню освоения
3. Объем дисциплины и виды
4. Содержание дисциплины
4.2. Содержание разделов дисциплины
4.3. Контрольные работы
Обеспечение дисциплины
5.2. Средства обеспечения освоения дисциплины
6. Методические рекомендации
Титульный лист контрольной работы оформляют в соответствии с прил. 1.
7. Задание на контрольную работу
T – интервала времени между двумя последовательными вызовами в потоке; б) вероятность того, что за t
8. Защита контрольных работ
9. Сдача экзамена по курсу
Билет № 45
Случайные числа
Методические указания для студентов
Методические указания для преподавателей
Материалы текущего, промежуточного, итогового контроля
Пример экзаменационных билета и задачи
...
Полное содержание

Подобный материал:

Автор-составитель:

Карпухин В.Б., доктор физико-математических наук, профессор кафедры «Высшая и прикладная математика»

Учебно-методический комплекс по дисциплине «Теория массового обслуживания» составлен в соответствии с требованиями Государственного образовательного стандарта высшего профессионального образования по специальности: 230101, вычислительные машины, комплексы, системы и сети (ЭВМ); 230201, информационные системы и технологии (ИСЖ);210100, управление и информатика в технических системах (УИТС).

Дисциплина входит в федеральный компонент цикла математических и естественнонаучных дисциплин и является обязательной для изучения.

1. ЦЕЛЬ ИЗУЧЕНИЯ ДИСЦИПЛИНЫ

Дисциплина «Теория массового обслуживания» имеет своей целью сформировать теоретико-вероятностный подход к изучению вычислительных систем, к оценке и определению их точности, быстродействия, надежности.

Применение современных средств вычислительной техники тесно связано с использованием возможностей методов теории случайных процессов и теории массового обслуживания. Для вычислительных систем характерна работа в режиме решения потока случайных задач, поступающих в случайные моменты времени. Случайность характерна и для отдельных подсистем типа «процессор – основная память», для обращения к внешним запоминающим устройствам и т. п. Анализ и синтез таких систем возможен методами теории массового обслуживания.

Задача анализа состоит в определении количественных показателей функционирования систем массового обслуживания и зависимости этих показателей от параметров входящего потока и структуры самой системы массового обслуживания, в определении «узких мест» системы и их влияния на эффективность работы всей СМО.

Задача синтеза состоит в определении структуры системы массового обслуживания при заданных свойствах и ограничениях на ресурсы системы.

Эти задачи могут быть решены как точными методами (марковские системы) так и методами имитационного моделирования. Ясно, что оба подхода к расчету вычислительных систем, как систем массового обслуживания, требуют знания такого математического аппарата, как теория массового обслуживания.

2. ТРЕБОВАНИЯ К УРОВНЮ ОСВОЕНИЯ

СОДЕРЖАНИЯ ДИСЦИПЛИНЫ

Изучив дисциплину «Теория массового обслуживания» студент должен:

2.1. Знать и уметь использовать при решении прикладных задач основы марковской теории и методов статистического моделирования систем массового обслуживания.

2.2. Иметь опыт и навыки решения задач по всем темам рабочей программы.

2.3. Иметь представление о способах математического описания реальных случайных процессов и их моделировании средствами теории массового обслуживания; о трудностях построения математических моделей систем массового обслуживания при потере марковости.

3. ОБЪЕМ ДИСЦИПЛИНЫ И ВИДЫ
УЧЕБНОЙ РАБОТЫ

Ниже приводится выписка из учебных планов специальностей ЭВМ, УИТС и ВИСЖ.

Вид учебной работы	Количество часов
Вид учебной работы	ЭВМ	УИТС	ВИСЖ
Аудиторные занятия:	12	12	48
лекции	8	8	24
практические занятия	4	4	24
Контрольная работа	115	115	13=3
Самостоятельная работа	58	48	100
Вид итогового контроля	Экзамен	Экзамен	Экзамен
Общая трудоемкость дисциплины	85	75	151

4. СОДЕРЖАНИЕ ДИСЦИПЛИНЫ

4.1. Разделы дисциплины и виды занятий

Для студентов-заочников специальностей ЭВМ и УИТС рекомендуется следующее распределение часов аудиторной работы.

Раздел дисциплины	Количество часов
Раздел дисциплины	лекции	практические занятия
Теория потоков. Простейший поток. Потоки событий, не являющиеся простейшими	2	1
Цепи Маркова с конечным числом состояний с дискретным временем, с непрерывным временем	2	1
Основные понятия теории массового обслуживания. Марковские СМО	2	1
Немарковские СМО. Имитационное моделирование СМО	2	1
Итого: лекций практических занятий	8	4
Всего аудиторных занятий	12

Для студентов-вечерников специальности ИСЖ рекомендуется следующее распределение часов аудиторной работы.

Раздел дисциплины	Количество часов
Раздел дисциплины	лекции	практические занятия
Простейший поток. Потоки событий, не являющиеся простейшими	2	2
Понятие случайного процесса. Дискретные цепи Маркова	2	2
Непрерывные цепи Маркова. Классификация состояний системы	2	2
Понятие об эргодическом процессе. Теорема Маркова и ее следствия	2	2
Процесс «гибели и размножения». Условия существования стационарного распределения	2	2
Основные понятия ТМО. Классификация СМО	2
Параметры и показатели эффективности работы СМО	2
Марковские СМО. Задача Эрланга	2	2
Основные типы марковских систем	2	4
Простейшие немарковские системы	2	2
Понятие о методе статистического моделирования	2	4
Имитационное моделирование СМО	2	2
Итого: лекций практических занятий	24	24
Всего аудиторных занятий	48

4.2. Содержание разделов дисциплины

Раздел 1

Теория потоков

1. Поток событий. Простейший поток и его свойства: стационарность, ординарность, отсутствие последствия.

[ 1, гл.5, § 5.9, гл. 19, § 19.3; 5, гл. VI, § 5; 6, задачи 184 - 187; 7; 9, гл. 11, § 11.2; 10, гл. 17, § 17.3; 11, гл. 10, § 10.2]

2. Потоки событий, не являющиеся простейшими: нестационарный пуассоновский поток, потоки Эрланга; регулярный поток; поток Пальма. Предельная теорема для суммарного потока.

[ 1, гл. 19, § 19.4, 19.5; 2, гл. 2, § 2.1-2.4; 7, задачи 11-20; 12, введение, § 3; 13, гл. 4, § 4.3, 4.11; гл. 7, § 7.2]

Раздел 2

Цепи Маркова

3. Понятие случайного процесса. Цепь Маркова с конечным числом состояний и дискретным временем. Граф состояний. Матрица переходных вероятностей. Стационарное распределение.

[2, гл. 3, § 3.2-3.3, 5, гл. XXII, §1-3, задачи 1,2; 7, задачи 21-30; 13, гл. 2, § 2.9]

4. Марковские процессы с конечным числом состояний и непрерывным временем. Размеченный граф состояний. Матрица интенсивностей перехода. Система дифференциальных уравнений Колмогорова. Нахождение стационарного распределения.

[ 2, гл. 4, §4.1-4.2; 3, гл. 5, § 15-17; 7, задачи 31-40; 11, гл. 10, § 10.3; 12, введение, § 4; 13, гл. 2, § 2.4]

5. Классификация состояний системы: источники, поглотители, транзитивные и изолированные состояния. Понятие об эргодическом процессе. Теорема Маркова (без доказательства) и ее применение для расчета финальных вероятностей состояний.

[ 2, гл. 3, § 3.1; 7, задачи 41-50; 13, гл.2, § 2.6, 2.7]

6. Процесс «гибели и размножения» с непрерывным временем и простейшими потоками, размеченный граф состояний. Условия существования стационарного режима. Нахождение предельного распределения вероятностей в случае конечного числа состояний.

[ 2, гл.5, § 5.1; 4, гл.1, §1.3,1.4; 7, задачи 51-60; 10, гл. 17, § 17.4 – 17.5; 11,гл. 10, § 10.4; 12, гл.1, § 1 ]

Раздел 3

Расчет простейших систем массового обслуживания

7. Основные понятия и классификация систем массового обслуживания (СМО): по поведению заявки (с отказами, с очередью, смешанного типа); по характеру источника заявок (открытого и замкнутого типа); по дисциплине ожидания и обслуживания.

[ 4, гл.1, § 1.2, 1.5-1.8; 3, гл.6, §18; 7; 9, гл. 11, § 11.1; 10, гл. 17, § 17.2; 11, гл. 10, § 10.1 ]

8. Параметры и характеристики СМО; параметры входящего потока; параметры структуры СМО. Показатели эффективности СМО. Формула Литтла.

[ 3, гл.6, §19 ; 7; 9, гл. 11, § 11.2; 10, гл. 17, § 17.6; 11, гл. 10, § 10.5; 12, введение, § 5; 13, гл. 3, § 3.4]

9. Марковские СМО. Многоканальная СМО с отказами (задача Эрланга). Предельное распределение вероятностей состояний. Определение основных характеристик обслуживания. Одноканальная СМО с ограниченной очередью. Многоканальная СМО с ограниченной очередью. Одноканальная СМО с неограниченной очередью. Многоканальная СМО с неограниченной очередью.

[ 3, гл.6, § 20-21 ; 4 ; гл.1, § 1.4-1.8, гл.4, § 4.1-4.2 ; 7; 9, гл. 11, § 11.3-11.4 ; 10, гл. 17, § 17.6; 11, гл. 10, § 10.5 – 10.6; 12, гл.1, § 1 - 3]

10. Немарковские СМО. Одноканальная СМО с неограниченной очередью, простейшим входящим потоком и произвольным распределением времени обслуживания. Формулы Полячека-Хинчина. Расчет показателей эффективности.

[ 3, гл.6, § 21 ; 7, задачи 71-80; 10, гл. 17, § 17.7 – 17.8; 12, гл. 2 - 4, § 1 - 2 ]

Раздел 4

Статистическое моделирование систем массового обслуживания

11. Понятие о методе статистического моделирования (методе Монте-Карло). Случайные числа. Разыгрывание дискретной случайной величины. Метод обратных функций для разыгрывания непрерывной случайной величины. Приближенное разыгрывание нормальной случайной величины.

[ 5, гл. XXI, § 1-4 ; 6, гл.15, § 1, задачи 679-681, § 3, задачи 690, 697 ; 3, гл.7, § 22, 23 ; 4, гл.6. § 6.1 ]

12. Моделирование случайного потока событий. Моделирование простейшего потока. Моделирование потока с заданным эмпирическим распределением интервалов времени между двумя последовательными событиями в потоке.

[ 5, гл.XXI, § 7, 6, гл.15, § 7, задачи 730, 731; 3, гл.7, § 24;

4, гл.6, § 6.2; 12, введение, § 6 ] .

13. Моделирование работы СМО. Построение временных диаграмм функционирования СМО. Моделирование СМО с отказами. Моделирование СМО с конечным числом мест в очереди. Моделирование работы СМО с приоритетами. Примеры расчета показателей эффективности работы СМО методом Монте-Карло.

[ 5, гл.XXI, § 7, 6, гл.15, § 7, задачи 730, 731; 3, гл.7, § 24; 4, гл.6, § 6.4; 10, гл. 17, § 17.9; 11, гл. 10, § 10.7; 13, гл. 10,
§ 10.1 – 10.4 ] .

4.3. Контрольные работы

В процессе изучения дисциплины студенты-заочники специальностей ЭВМ и УИТС выполняют одну контрольную работу. По окончании изучения дисциплины студенты сдают зачет по контрольной работе и экзамен по курсу.

По окончании изучения дисциплины студенты-вечерники специальности ВИСЖ выполняют одну аудиторную контрольную работу и сдают экзамен по курсу.

5. УЧЕБНО-МЕТОДИЧЕСКОЕ
ОБЕСПЕЧЕНИЕ ДИСЦИПЛИНЫ

5.1. Рекомендуемая литература

Основная

Вентцель Е. С. Теория вероятностей, 2002.

2. Вентцель Е. С. Исследование операций: задачи, принципы, методология. – М.: Наука, 2001.

3. Гмурман В. Е. Теория вероятностей и математическая статистика. - М.: Высшая школа, 2003.

5. Гмурман В. Е. Руководство к решению задач по теории вероятностей и математической статистике. – М.: Высшая школа, 2002.

6. Гнеденко Б.В., Коваленко И.Н. Введение в теория массового обслуживания 2011

Дополнительная

Антонов А.В. Системный анализ. Учебник для студентов вузов, обучающихся по специальностям ИВТ и АСУ. – М.: Высшая школа, 2006.
Колемаев В.А, Староверов О.В., Турундаевский В.Б. Теория вероятностей и математическая статистика 1991.
Справочник по теории вероятностей и математической статистике. Справочное издание, 1985

5.2. Средства обеспечения освоения дисциплины

В процессе изучения дисциплины «Теория массового обслуживания» рекомендуется использовать современные версии пакетов прикладных программ Mathcad, Maple, Derive, Excel.

1. Очков В.Ф. Mathcad 14 для студентов, инженеров и конструкторов. – СПб.: БХВ – Петербург, 2007.

2. Ларсен Р.У. Инженерные расчеты в Excel. – М.: Вильямс, 2004.

3. Дьяконов В.П. Maple 9.5/10 в математике, физике и образовании. – М.: СОЛОН – Пресс, 2006.

4. Лобанова О.В. Практикум по решению задач в математической системе Derive - М.: Финансы и статистика, 1999.

6. МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
ПО ОРГАНИЗАЦИИ ИЗУЧЕНИЯ ДИСЦИПЛИНЫ

Контрольную работу студент-заочник выполняет в отдельной тетради. Текст пишут от руки обычной или шариковой ручкой чернилами или пастой одного цвета, но не красного и не зеленого. Каждая страница текста должна иметь поля не менее 30 мм для замечаний преподавателя.

Титульный лист контрольной работы оформляют в соответствии с прил. 1.

Все страницы, рисунки, таблицы, схемы, графики, должны иметь единую порядковую нумерацию. Графическую часть работы выполняют карандашом с применением чертежных инструментов на отдельной странице или миллиметровой бумаге. Допускается выполнение графической части на ЭВМ с соответствующими пояснениями в тексте. Все иллюстрации обозначаются номером сокращенно, например «Рис. 2.3». Цифровой материал представляют в виде таблиц. Каждая таблица должна иметь тематический заголовок. Таблицы нумеруют выше заголовка в верхнем правом углу, например «Таблица 1.3» .

В конце работы студент приводит список использованной при выполнении контрольной работы литературы и вычислительных средств, ставит личную подпись, а также дату сдачи работы на проверку.

Контрольные работы выполняют по варианту, номер которого совпадает с последней цифрой учебного шифра студента-заочника, и сдают преподавателю-рецензенту для проверки. Например, студент-заочник, имеющий учебный шифр 0510–п/ЭВМ–3428, выполняет задачи с номерами 8, 18, 28, …, содержащиеся в варианте 8. Если учебный шифр оканчивается на «0», то студент-заочник решает задачи варианта 10.

Преподаватель-рецензент проверяет правильность решения каждой задачи и в конце контрольной работы пишет рецензию на ее выполнение. В рецензии отмечают ошибки решения, проводят анализ их причин, дают рекомендации по более глубокому изучению учебного материала с целью исправления допущенных ошибок, указывают недостатки оформления контрольной работы и выносят заключение «Контрольная работа допущена к зачету» или «Контрольная работа не допущена к зачету». В той же тетради после рецензии преподавателя студент-заочник должен исправить допущенные ошибки и вновь сдать контрольную работу на проверку.

Зачет по контрольной работе студент-заочник может получить лишь после беседы с преподавателем.

Распределение номеров задач по вариантам контрольных работ приведено в таблице.

Вариант	Номера задач
01	1, 11, 21, 31, 41, 51, 61, 71
02	2, 12, 22, 32, 42, 52, 62, 72
03	3, 13, 23, 33, 43, 53, 63, 73
04	4, 14, 24, 34, 44, 54, 64, 74
05	5, 15, 25, 35, 45, 55, 65, 75
06	6, 16, 26, 36, 46, 56, 66, 76
07	7, 17, 27, 37, 47, 57, 67, 77
08	8, 18, 28, 38, 48, 58, 68, 78
09	9, 19, 29, 39, 49, 59, 69, 79
10	10, 20, 30, 40, 50, 60, 70, 80

Студент-вечерник выполняет одну аудиторную контрольную работу в конце семестра в течение двух академических часов. Содержание контрольных заданий определяется преподавателем, ведущим занятия в группе. Один контрольный вариант должен содержать 5-6 типовых задач (в зависимости от сложности). Далее приведенные контрольные задачи обязательны для студентов-заочников и служат материалом для самостоятельной подготовки к аудиторной контрольной работе для студентов-вечерников.

7. ЗАДАНИЕ НА КОНТРОЛЬНУЮ РАБОТУ

1–10. Среднее число вызовов, поступающих на станцию скорой помощи за один час, равно . Поток вызовов простейший. Найти:

а) математическое ожидание, дисперсию, среднее квадратическое отклонение непрерывной случайной величины T – интервала времени между двумя последовательными вызовами в потоке;

б) вероятность того, что за t минут поступит: m вызовов; менее m вызовов; не менее m вызовов.

1. = 60, t = 6, m = 3.

2. = 40, t = 6, m = 4.

3. = 30, t = 10, m = 2.

4. = 15, t = 12, m = 4.

5. = 30, t = 4, m = 3.

6. = 20, t = 9, m = 3.

7. = 35, t = 12, m = 4.

8. = 25, t = 12, m = 3.

9. = 10, t = 24, m = 2.

10. = 50, t = 6, m = 4.

11–20. Электронное устройство работает в ждущем режиме и переключается очередным импульсом. Поток импульсов является потоком Эрланга k – го порядка с интенсивностью

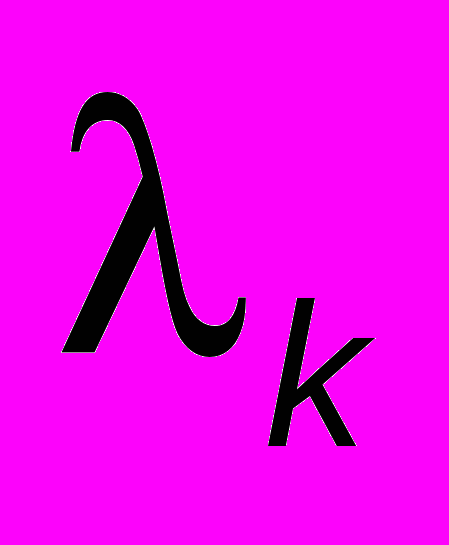импульсов в час. В случайный момент времени устройство включается в сеть и ждет первого очередного импульса. Найти плотность распределения вероятностей времени ожидания очередного импульса и построить ее график. Вычислить вероятность того, что устройство останется в ждущем режиме не более t минут. Ответ дать с тремя десятичными знаками.

Указание: плотность распределения времени ожидания первого очередного события для потока Эрланга k – го порядка имеет вид

f(x)= ,

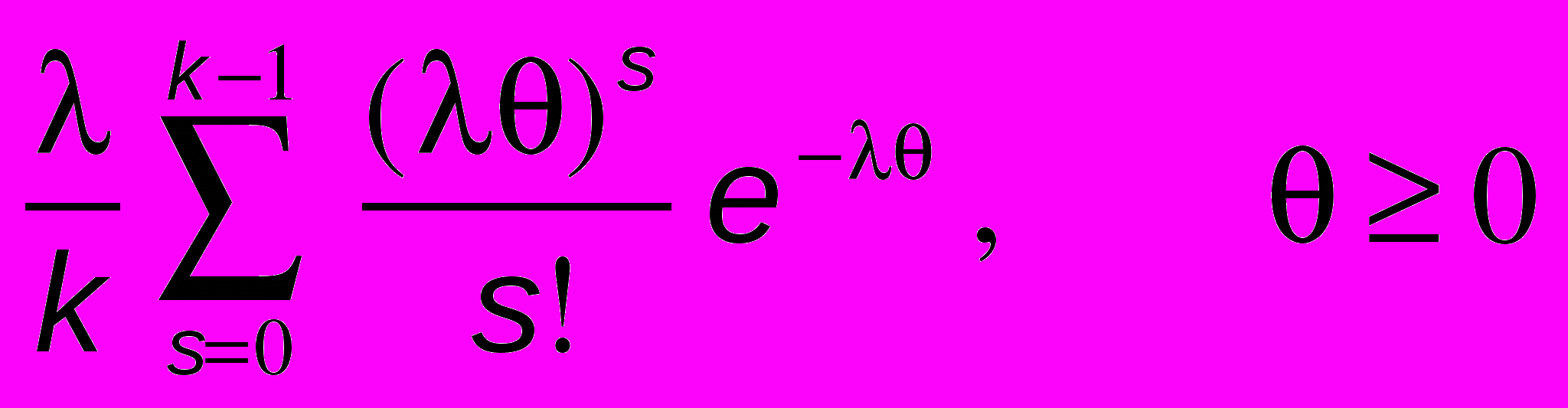где – интенсивность простейшего потока, из которого получен поток Эрланга k – го порядка.

11. k = 3,

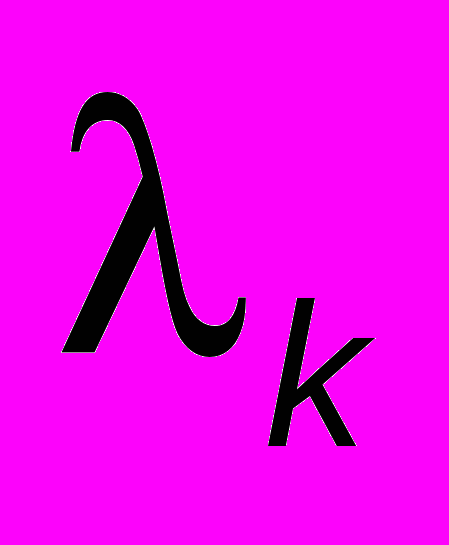= 2, t = 10.

12. k = 2,

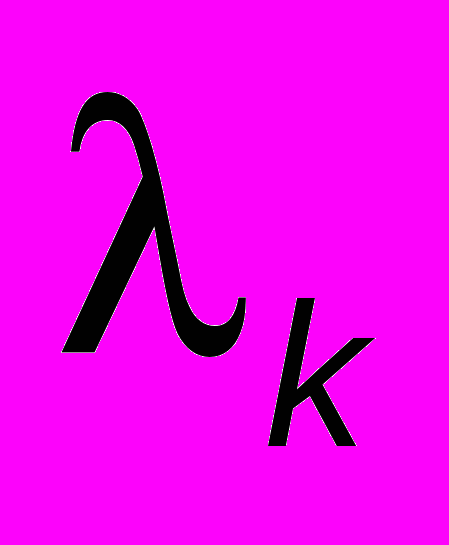= 3, t = 5.

13. k = 3,

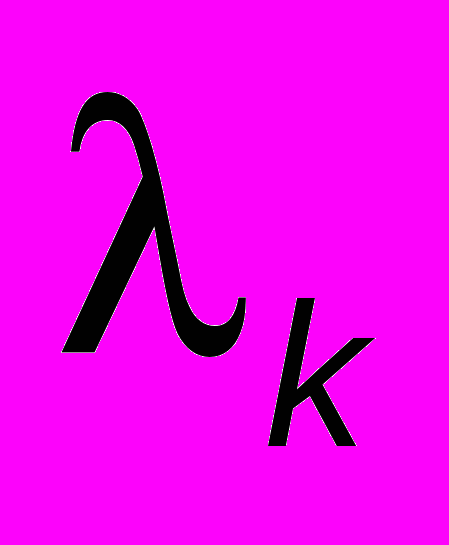= 1, t = 6.

14. k = 2,

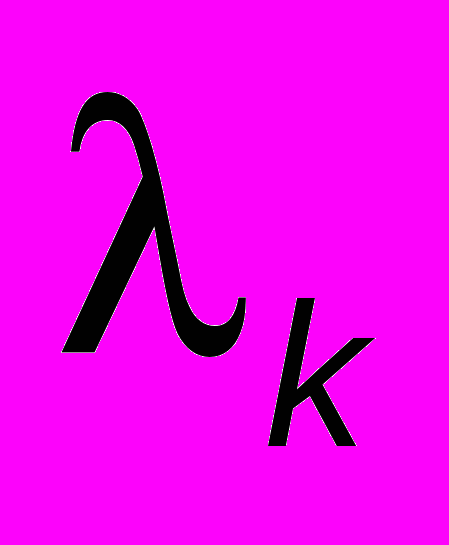= 2, t = 12.

15. k = 3,

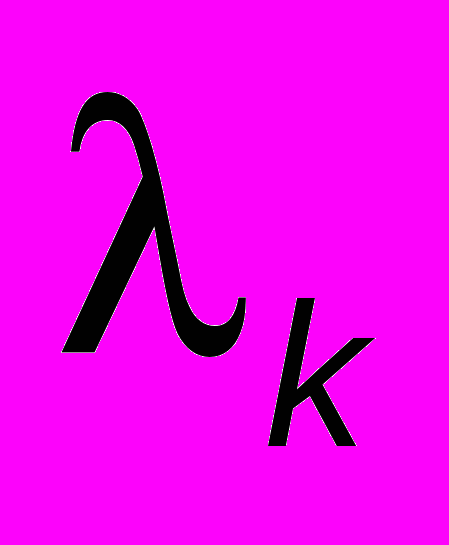= 3, t = 15.

16. k = 2,

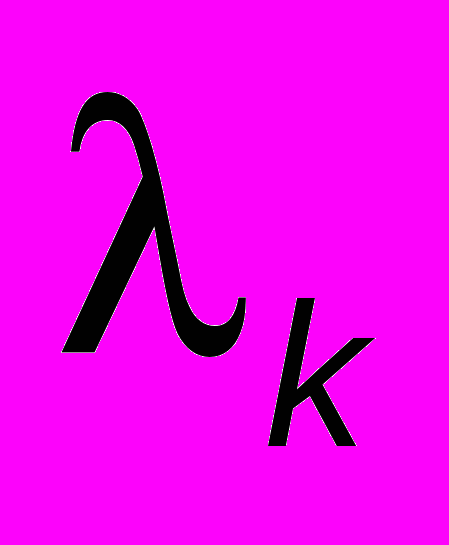= 0,5, t = 10.

17. k = 3,

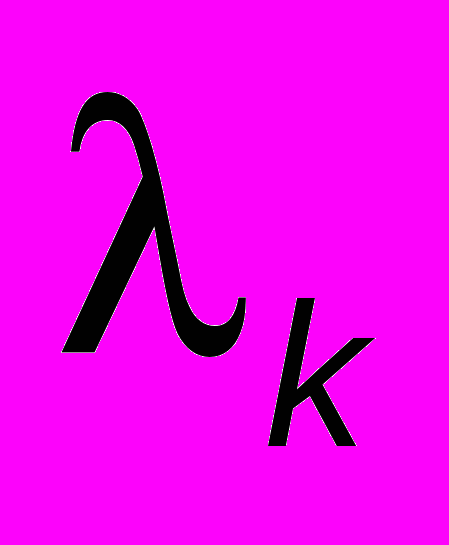= 1,5, t = 5.

18. k = 2,

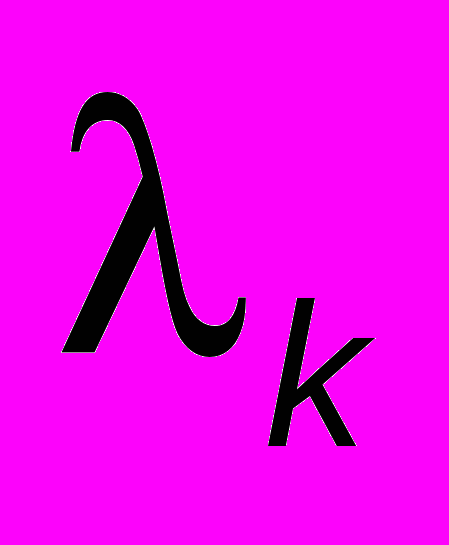= 2,5, t = 20.

19. k = 3,

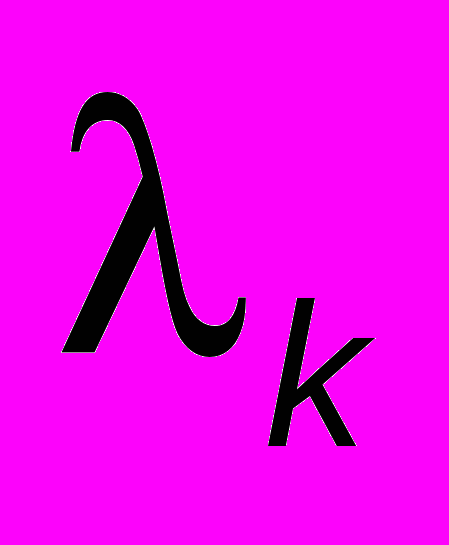= 0,5, t = 12.

20. k = 2,

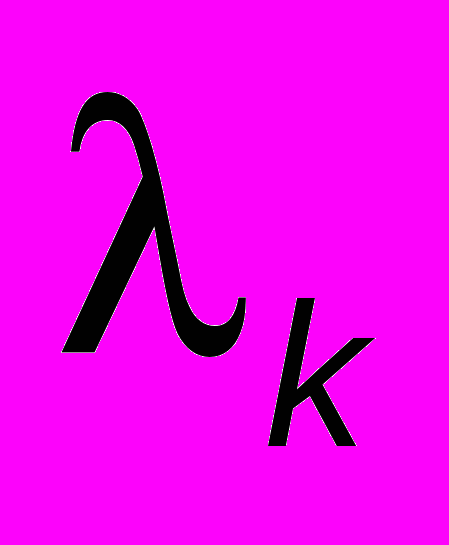= 1,5, t = 15.

21–30. Задана матрица P вероятностей перехода дискретной цепи Маркова за один шаг. Распределение вероятностей по состояниям в начальный момент определяется вектором

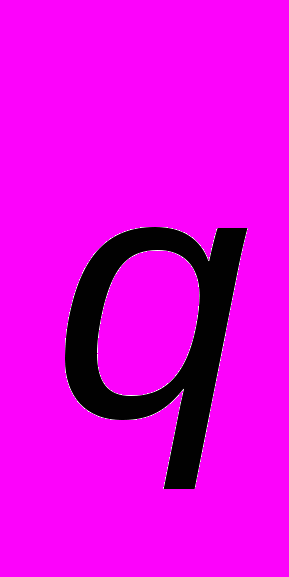. Построить размеченный граф состояний. Найти:

1) матрицу P₂ переходов цепи за два шага;

2) распределение вероятностей по состояниям в конце второго шага;

3) вероятность пребывания цепи в третьем состоянии в конце первого шага;

4) стационарное распределение вероятностей.

21. P = ,

.

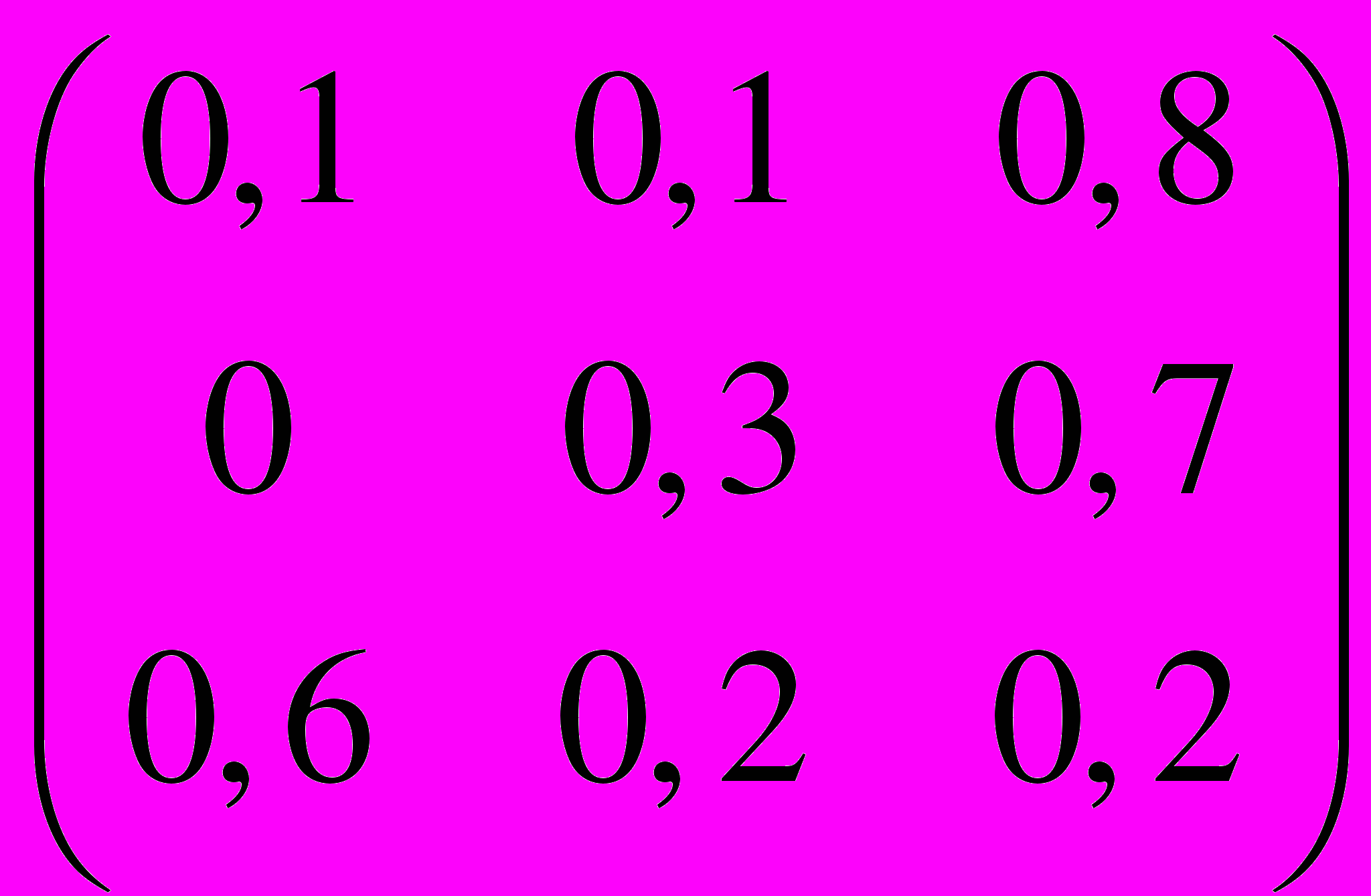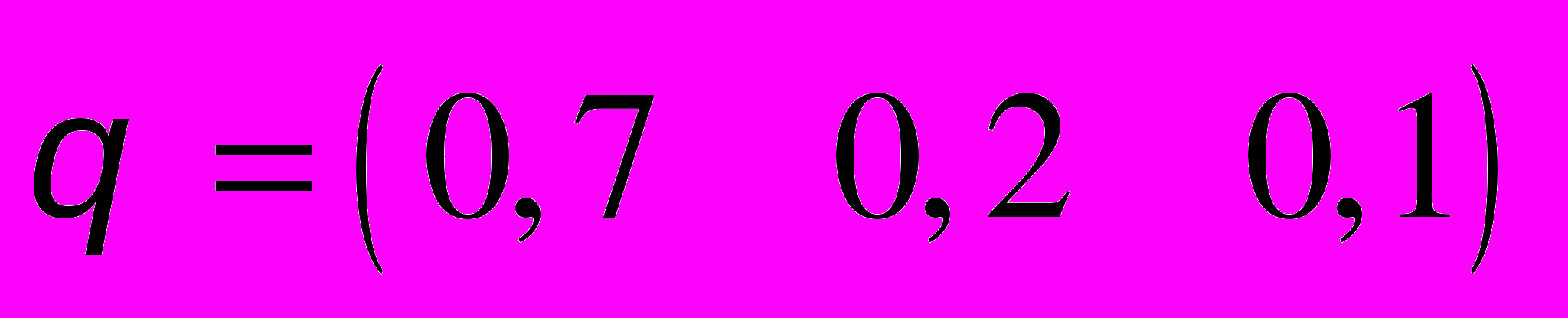22. P = ,

.

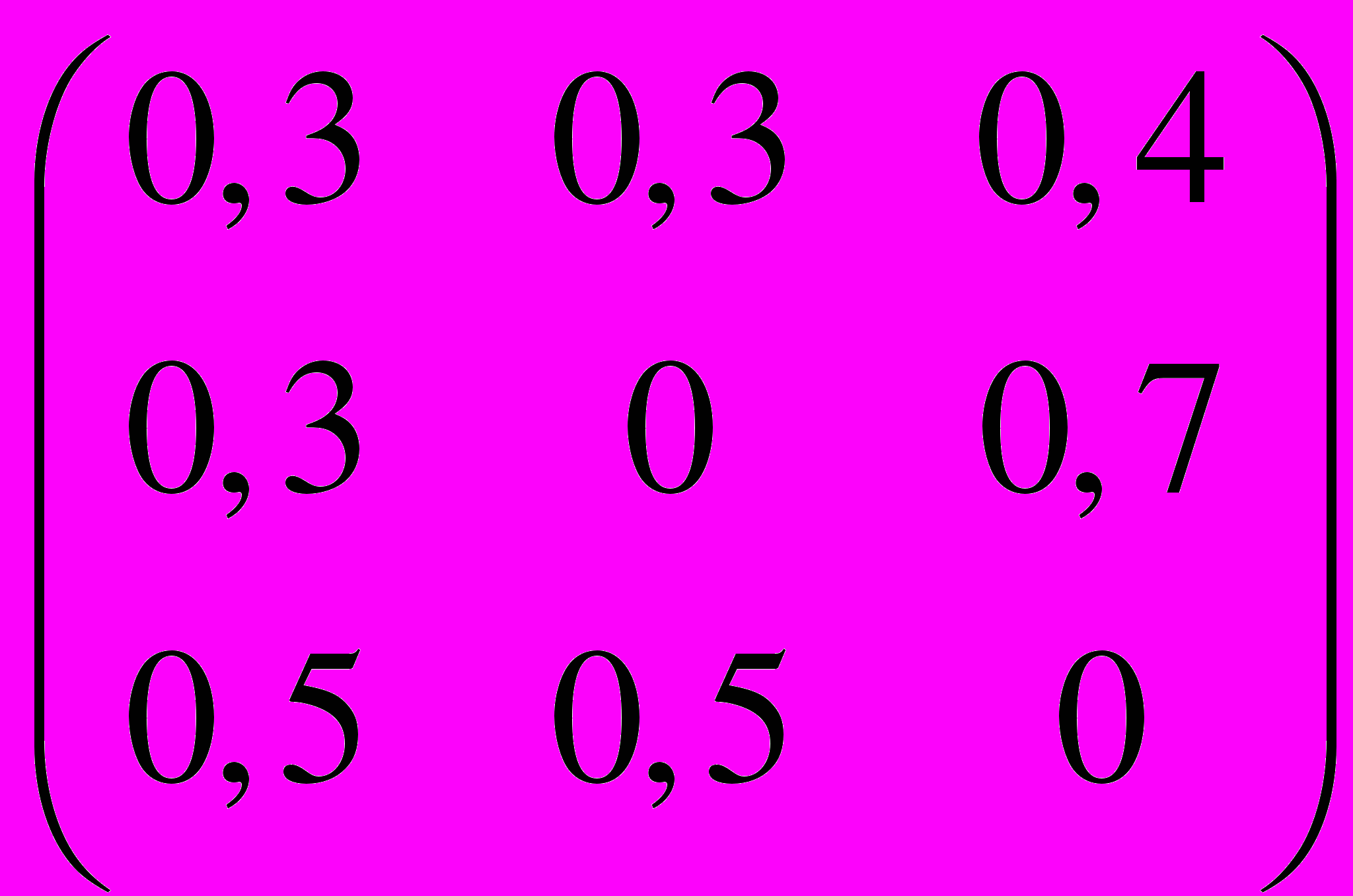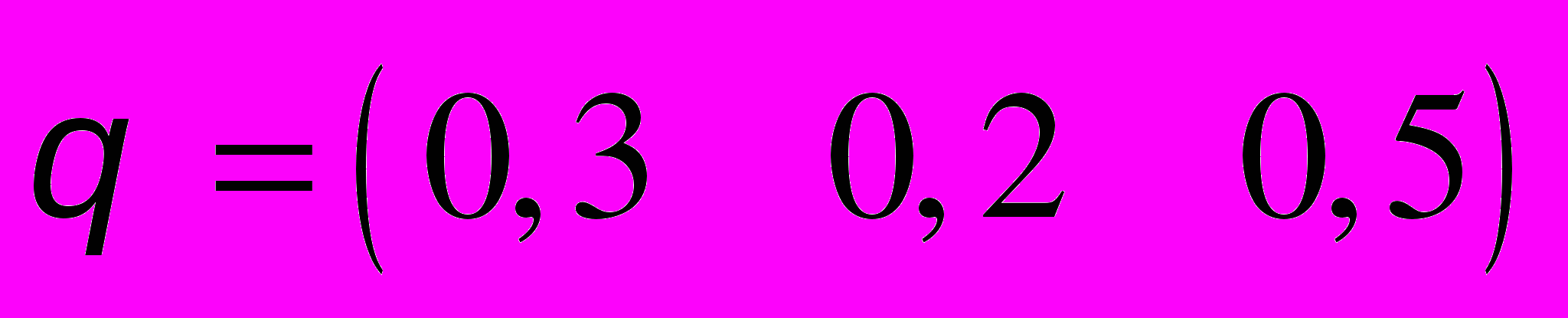23. P = ,

.

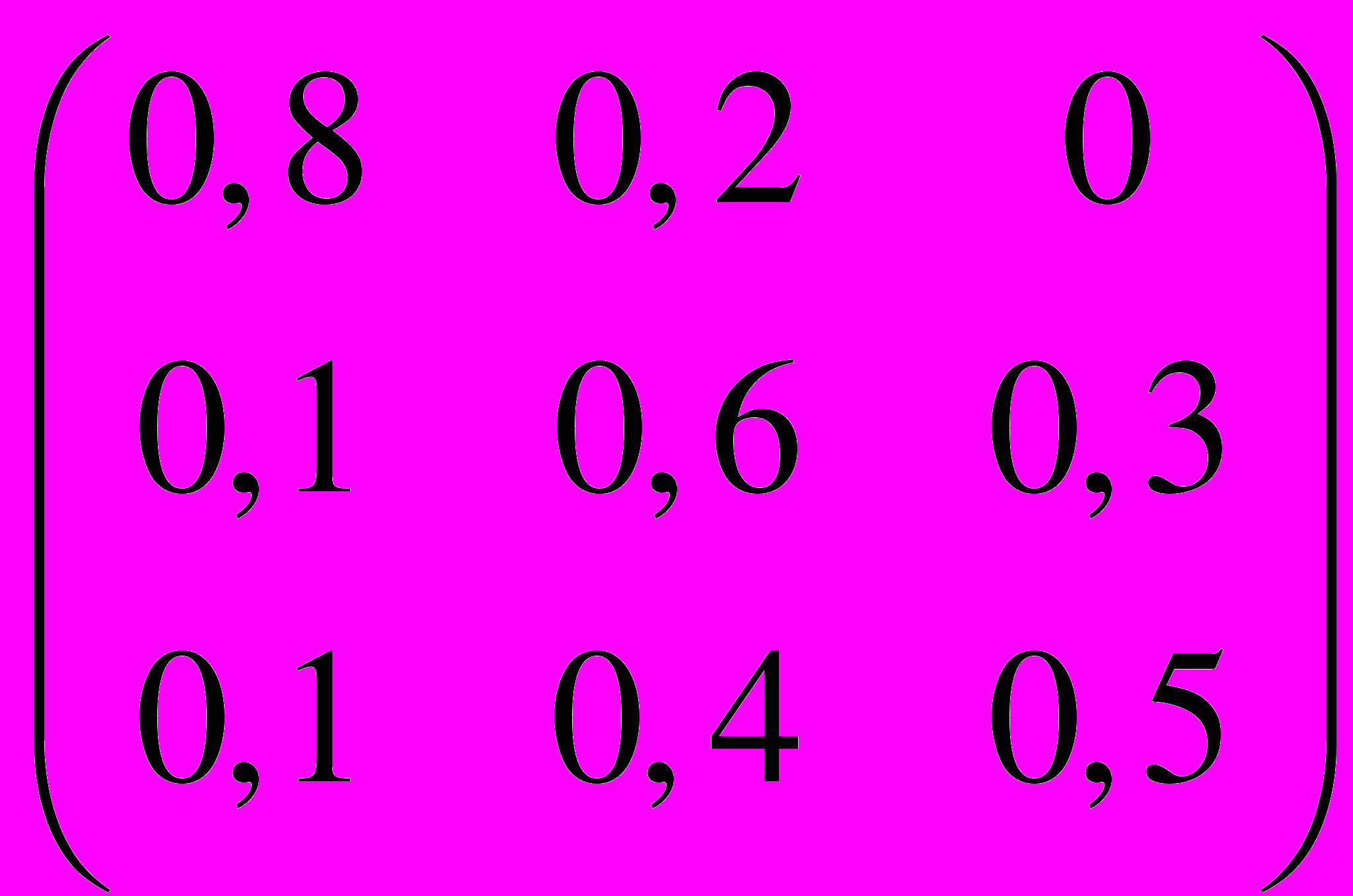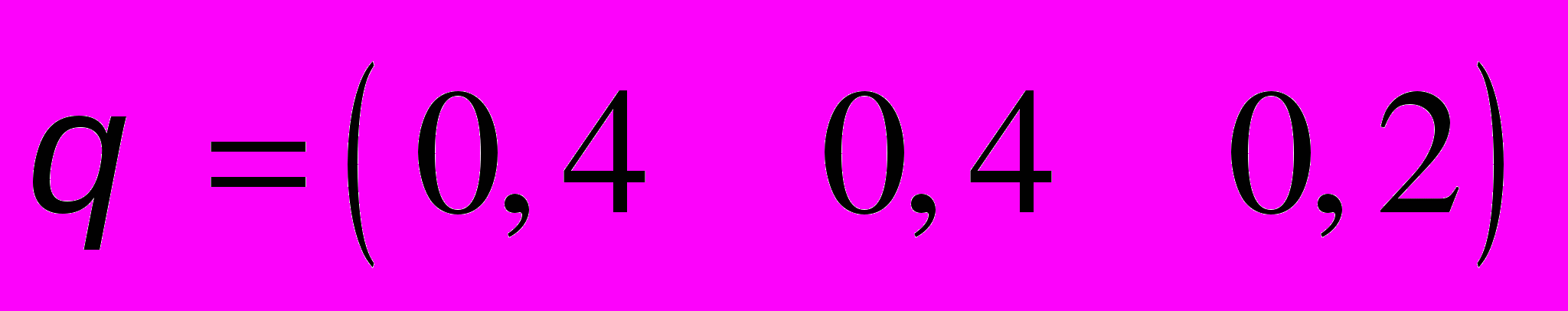24. P = ,

.

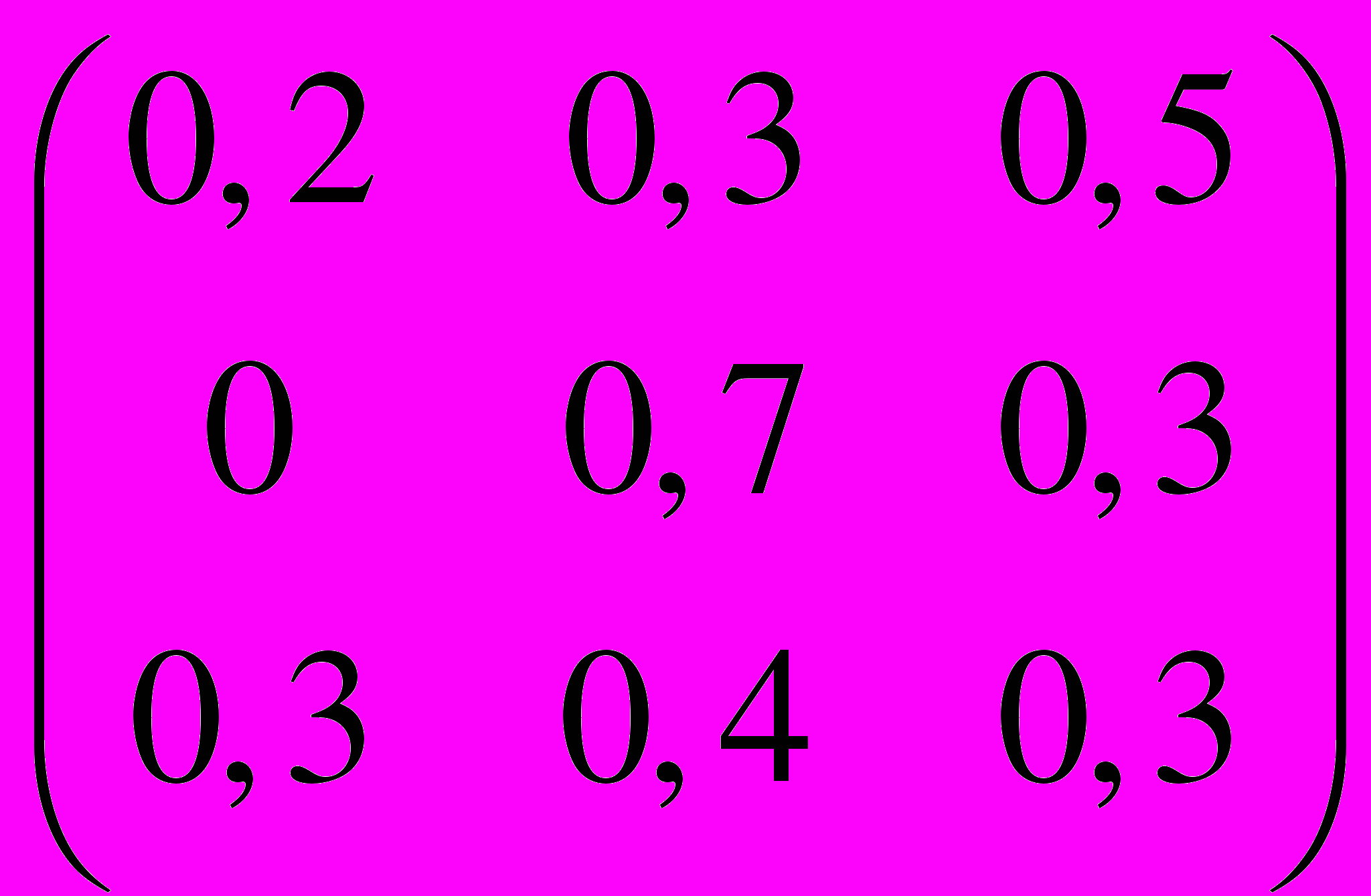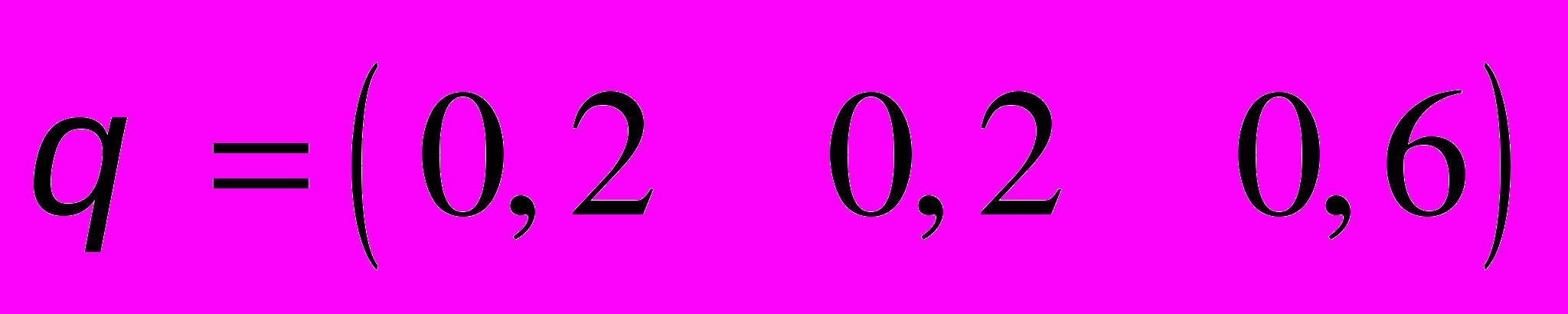25. P = ,

.

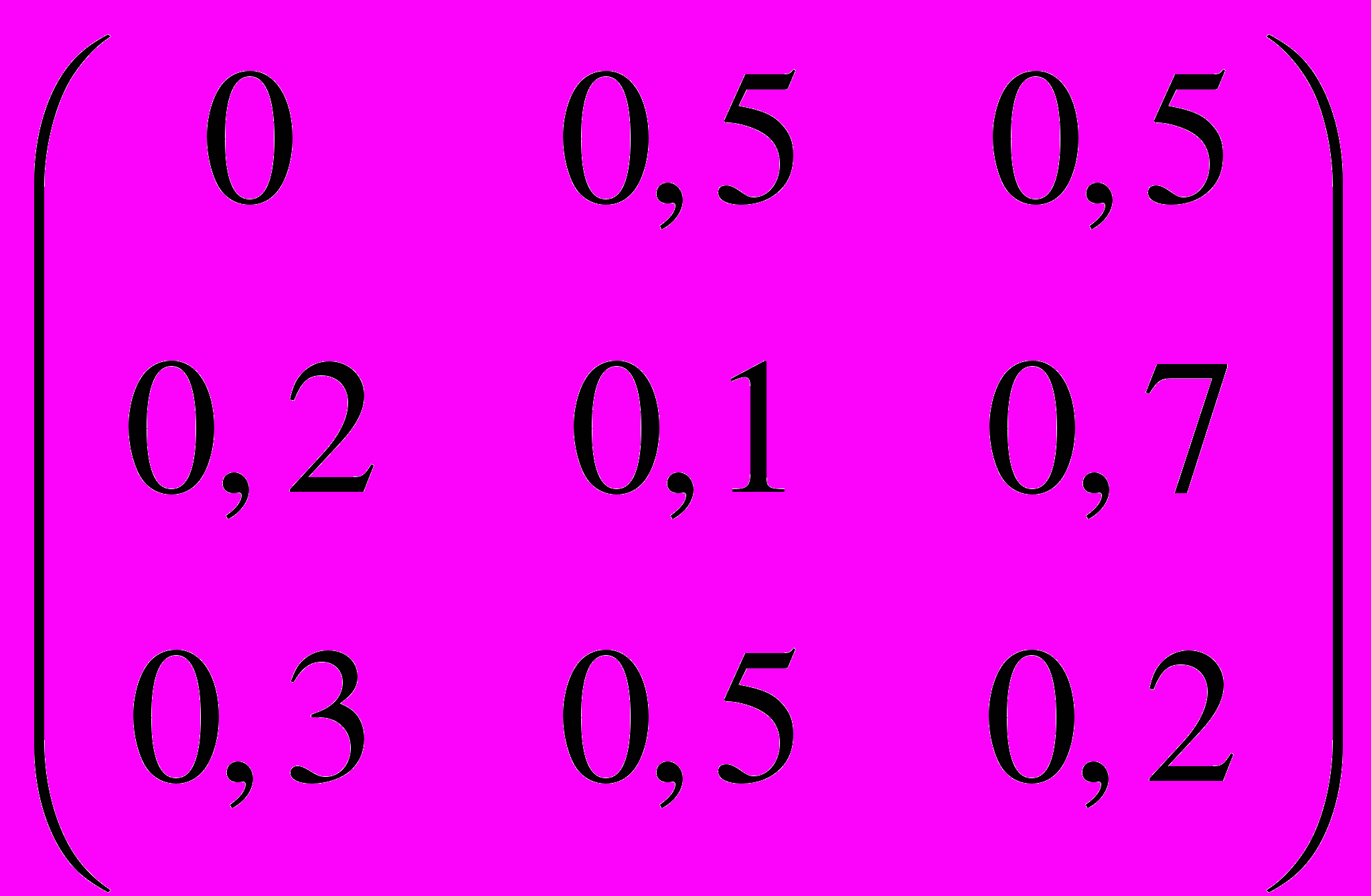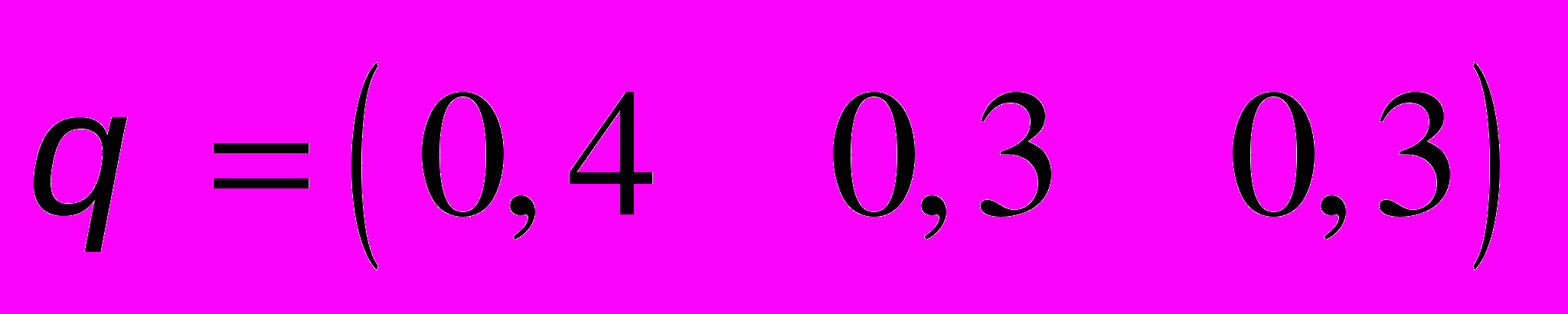26. P = ,

.

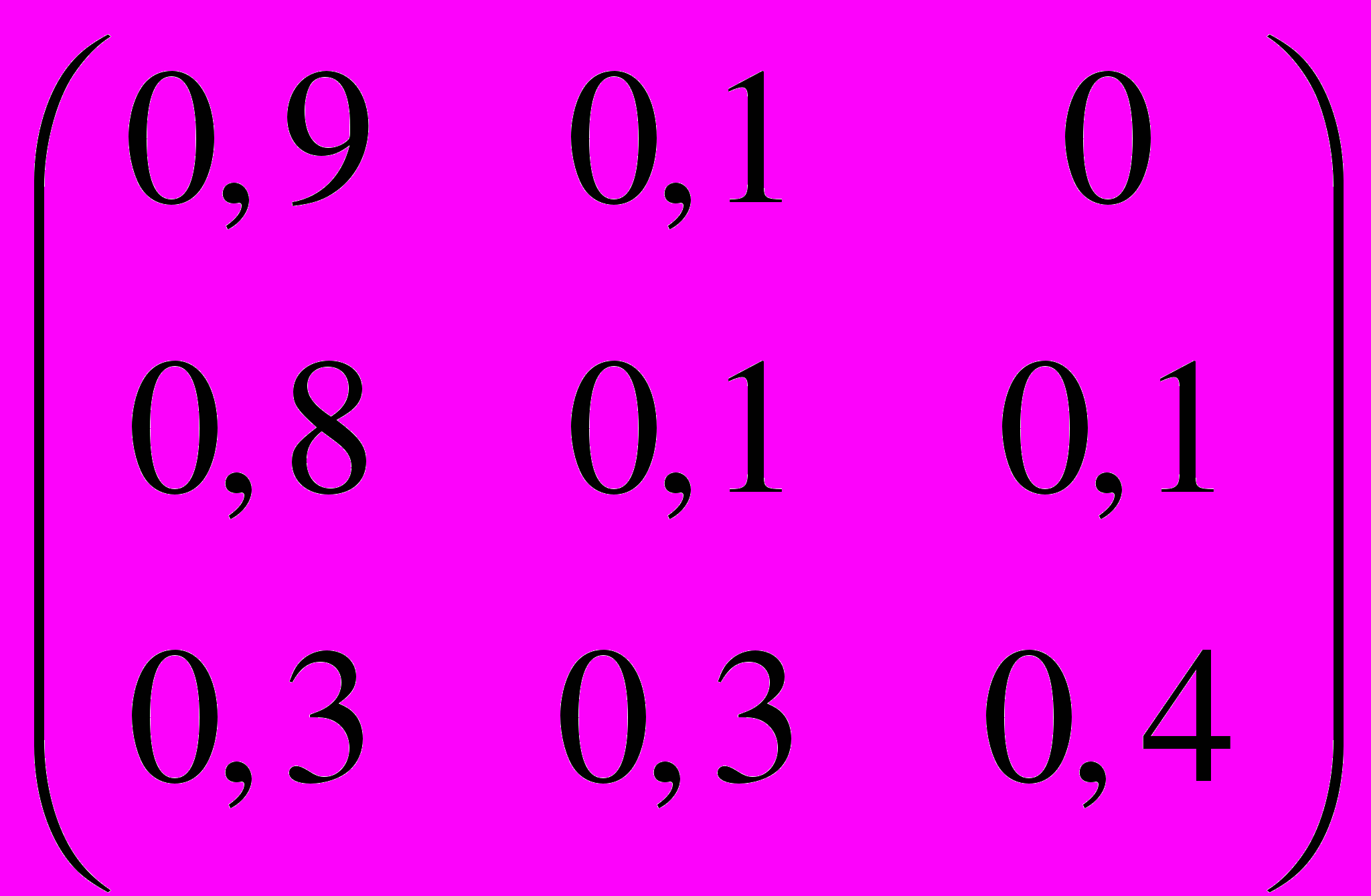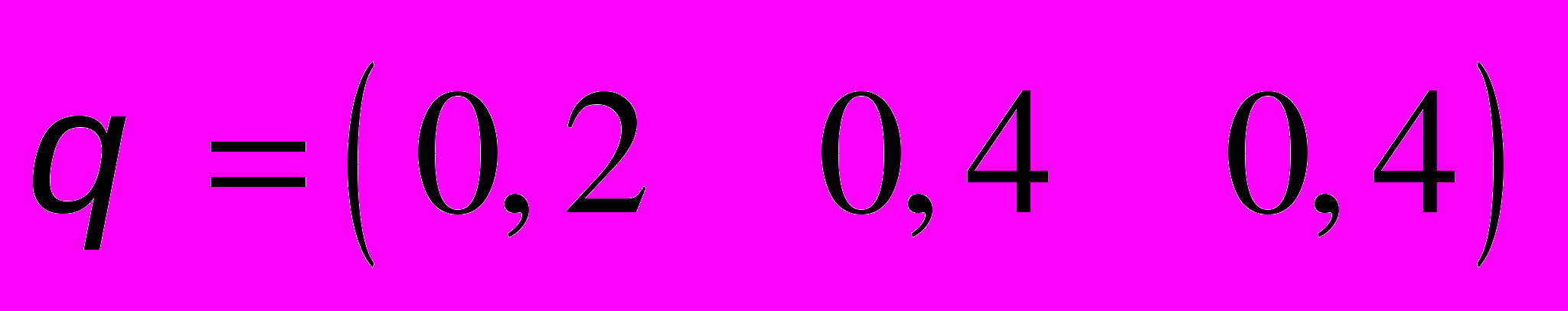27. P = ,

.

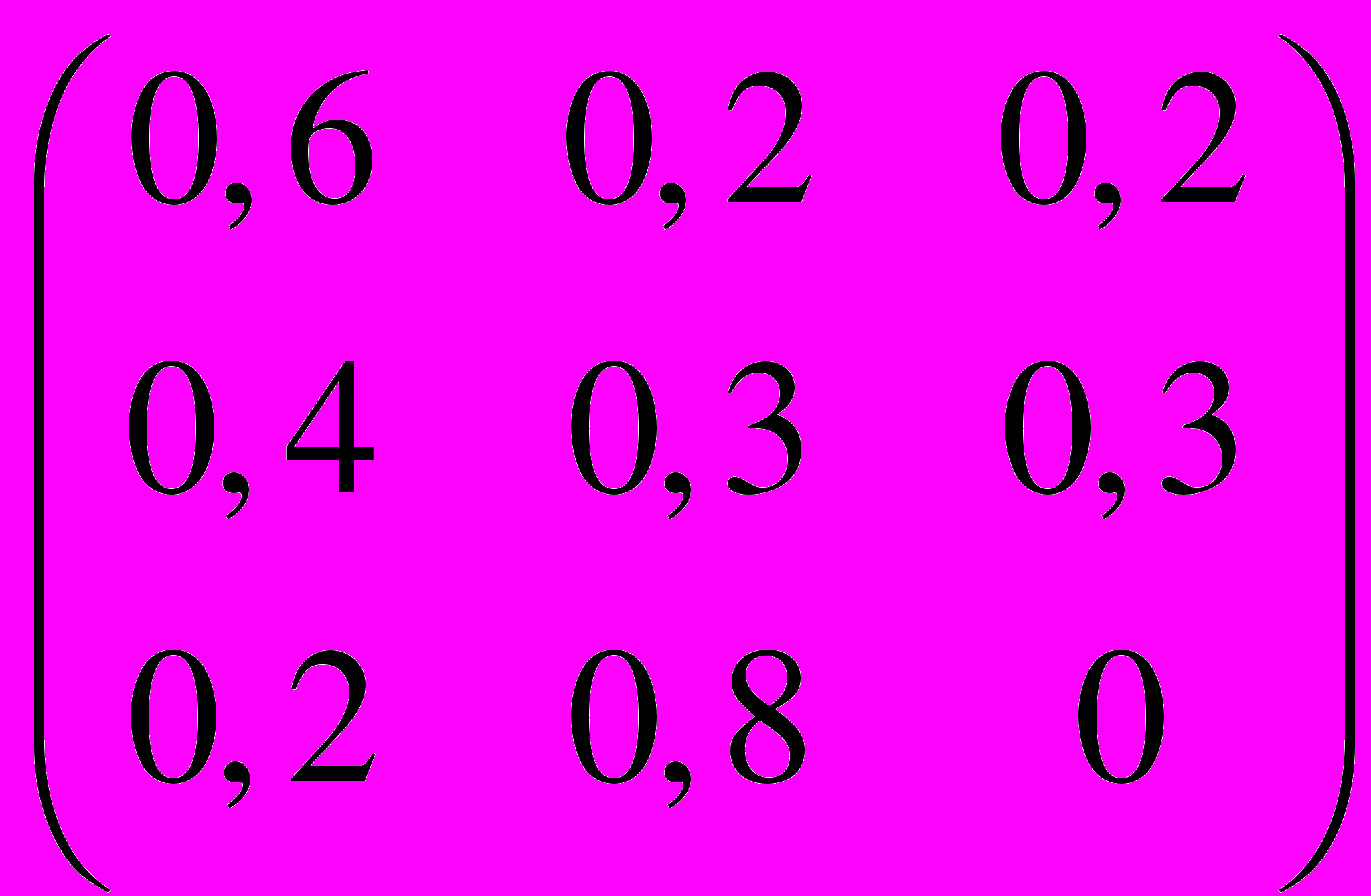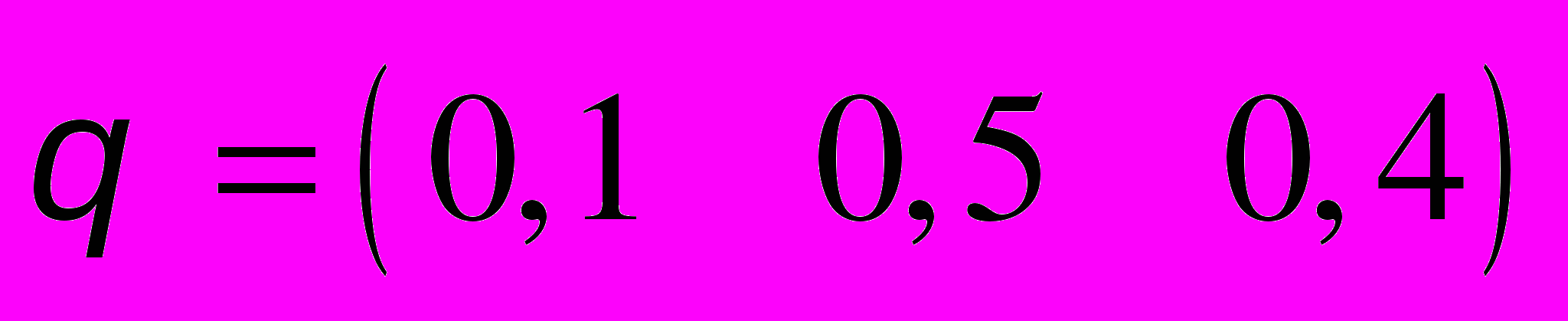28. P = ,

.

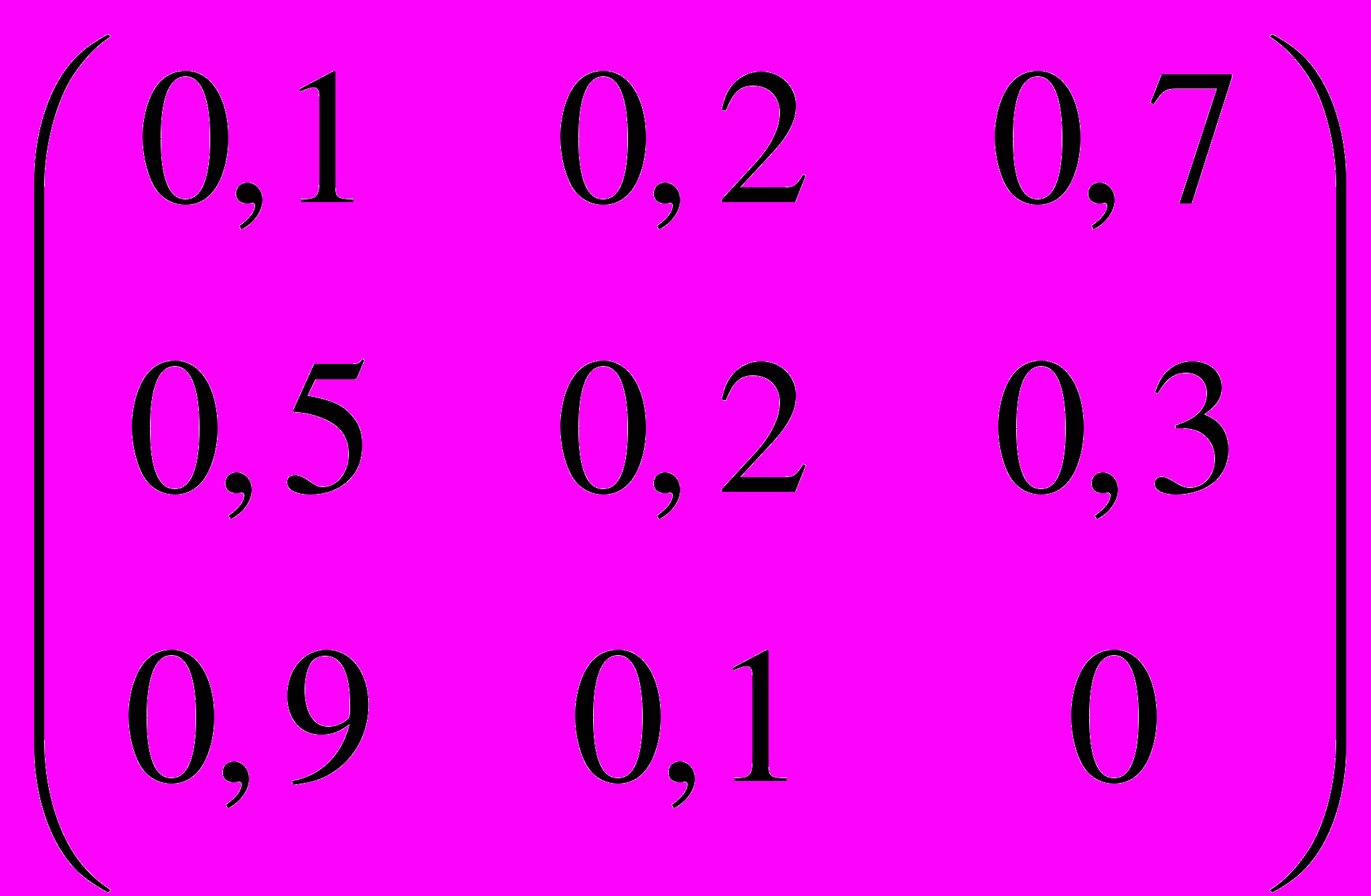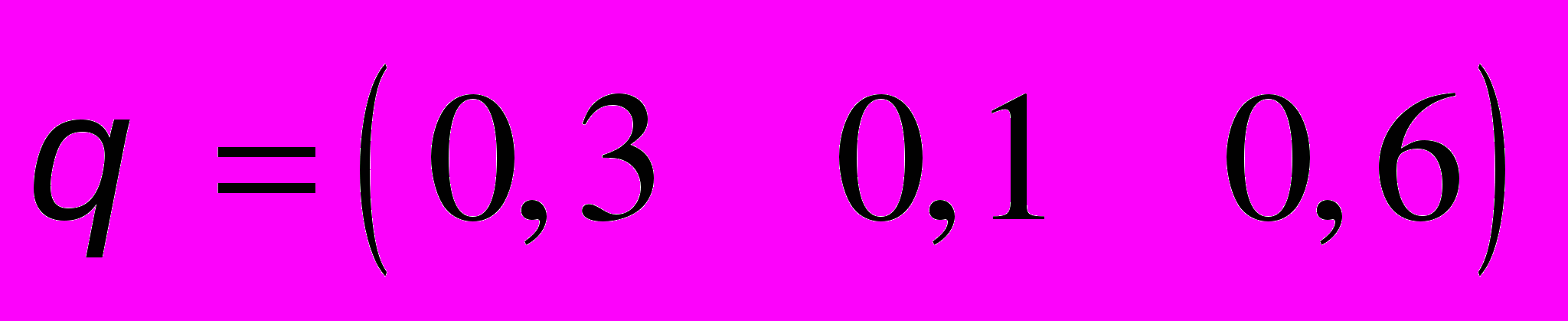29. P = ,

.

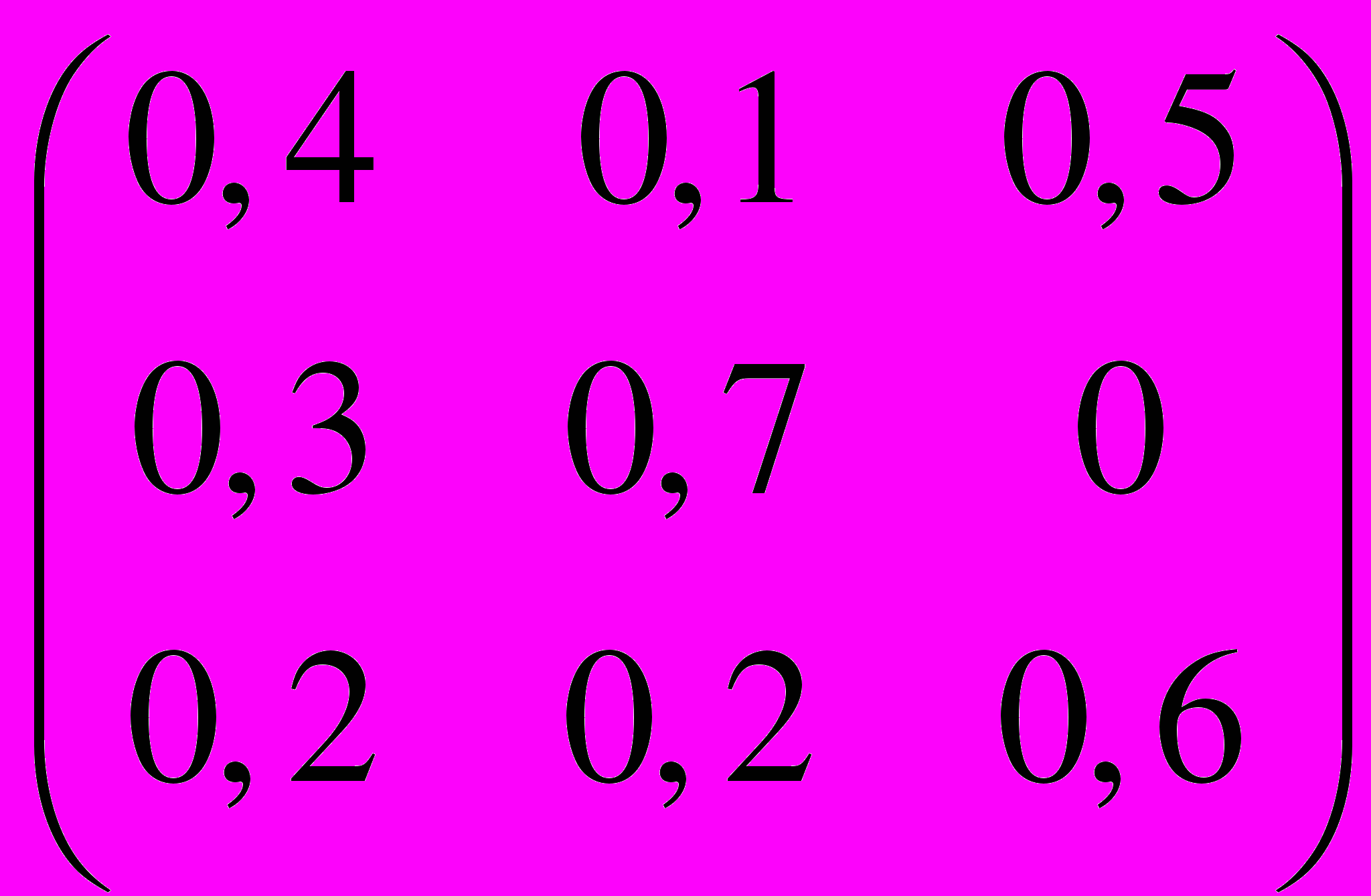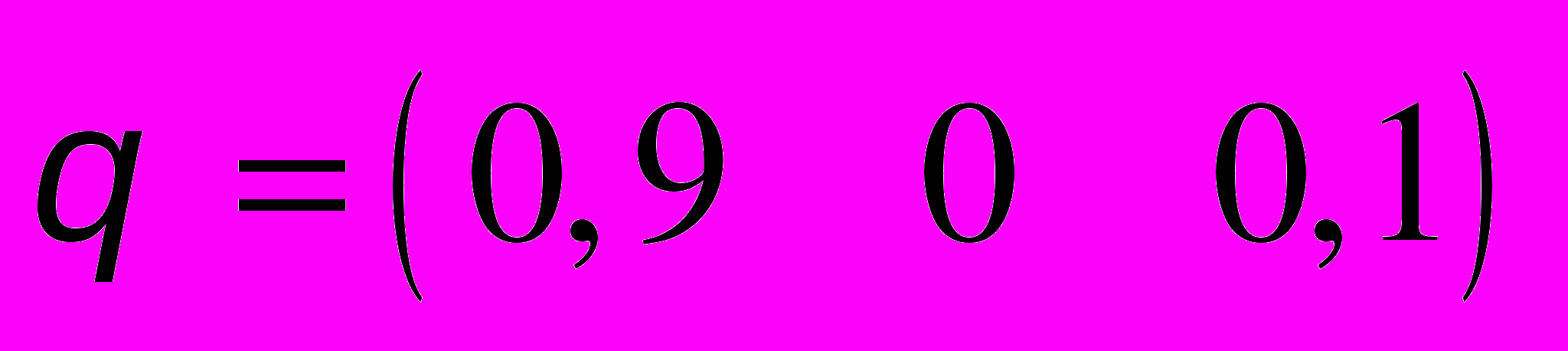30. P = ,

.

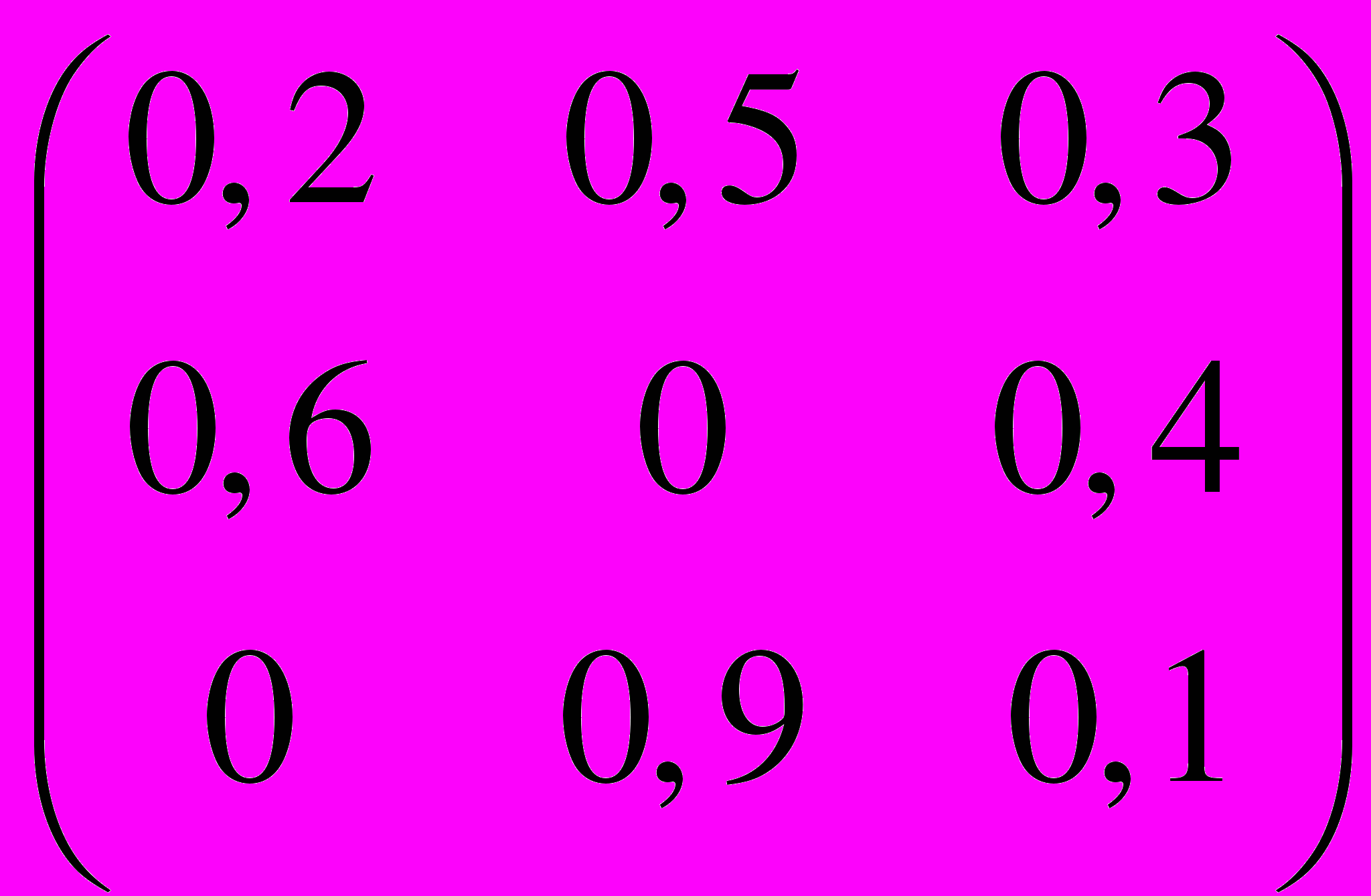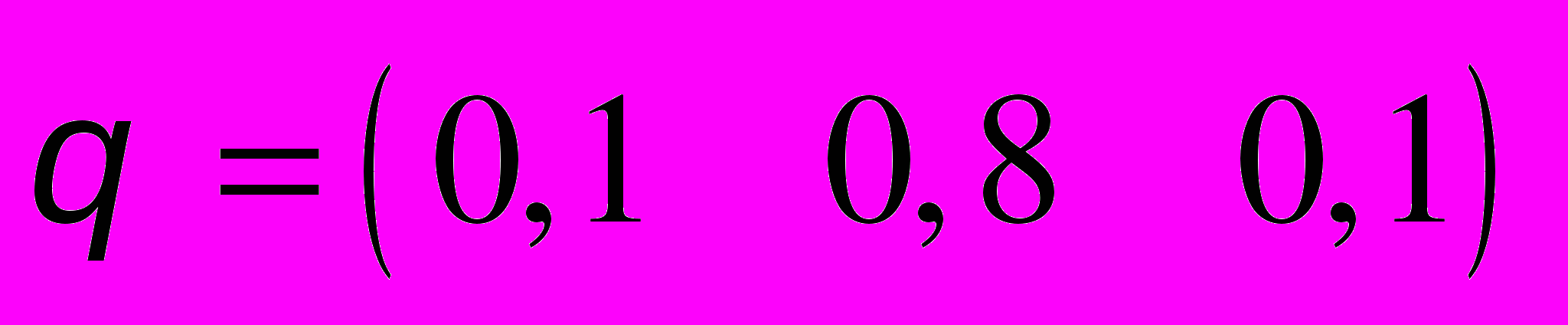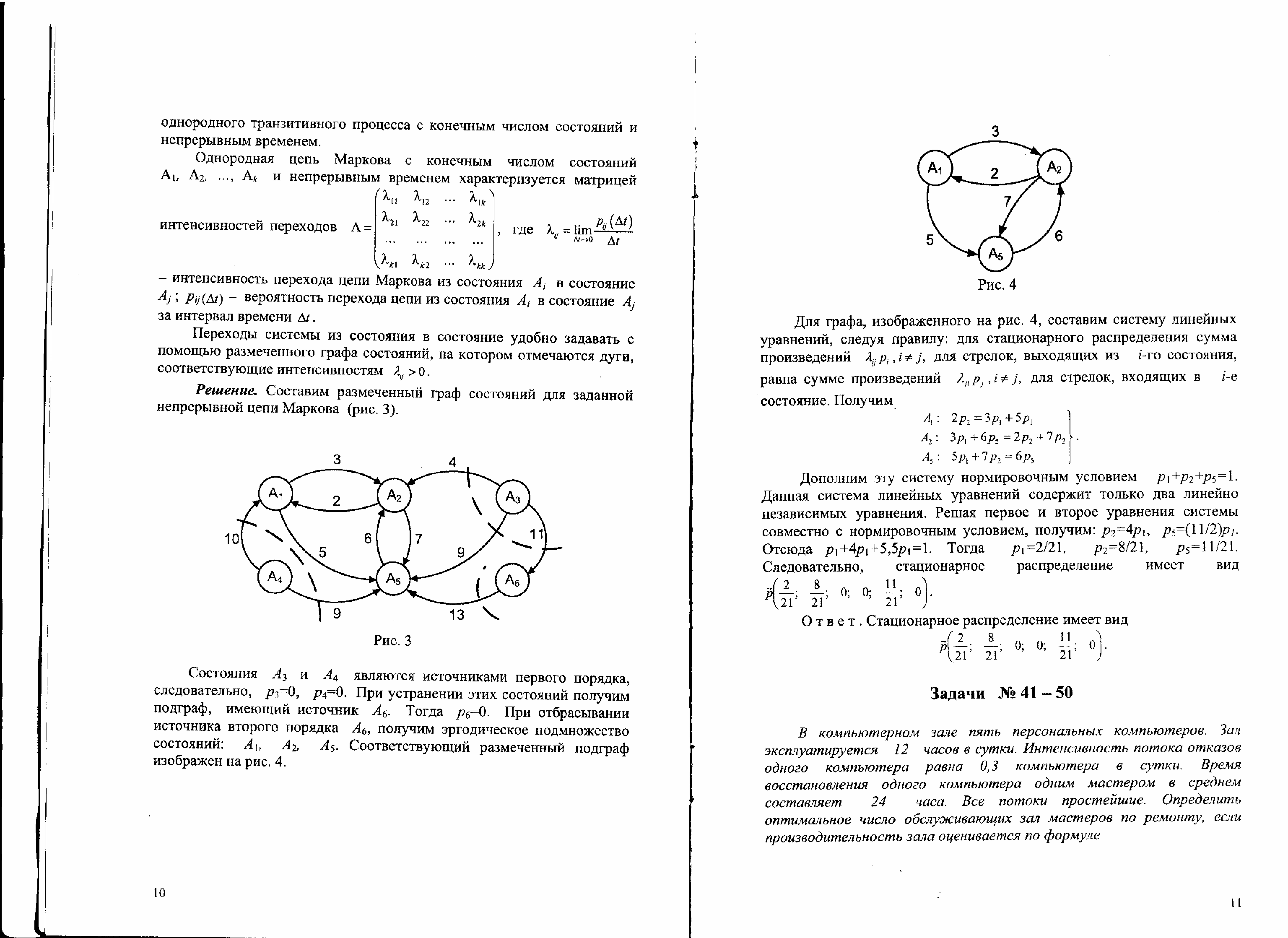
31 – 40. Задана матрица

интенсивностей переходов непрерывной цепи Маркова. Построить размеченный граф состояний. Провести классификацию состояний системы. Найти стационарное распределение вероятностей, если оно существует.

31.

.

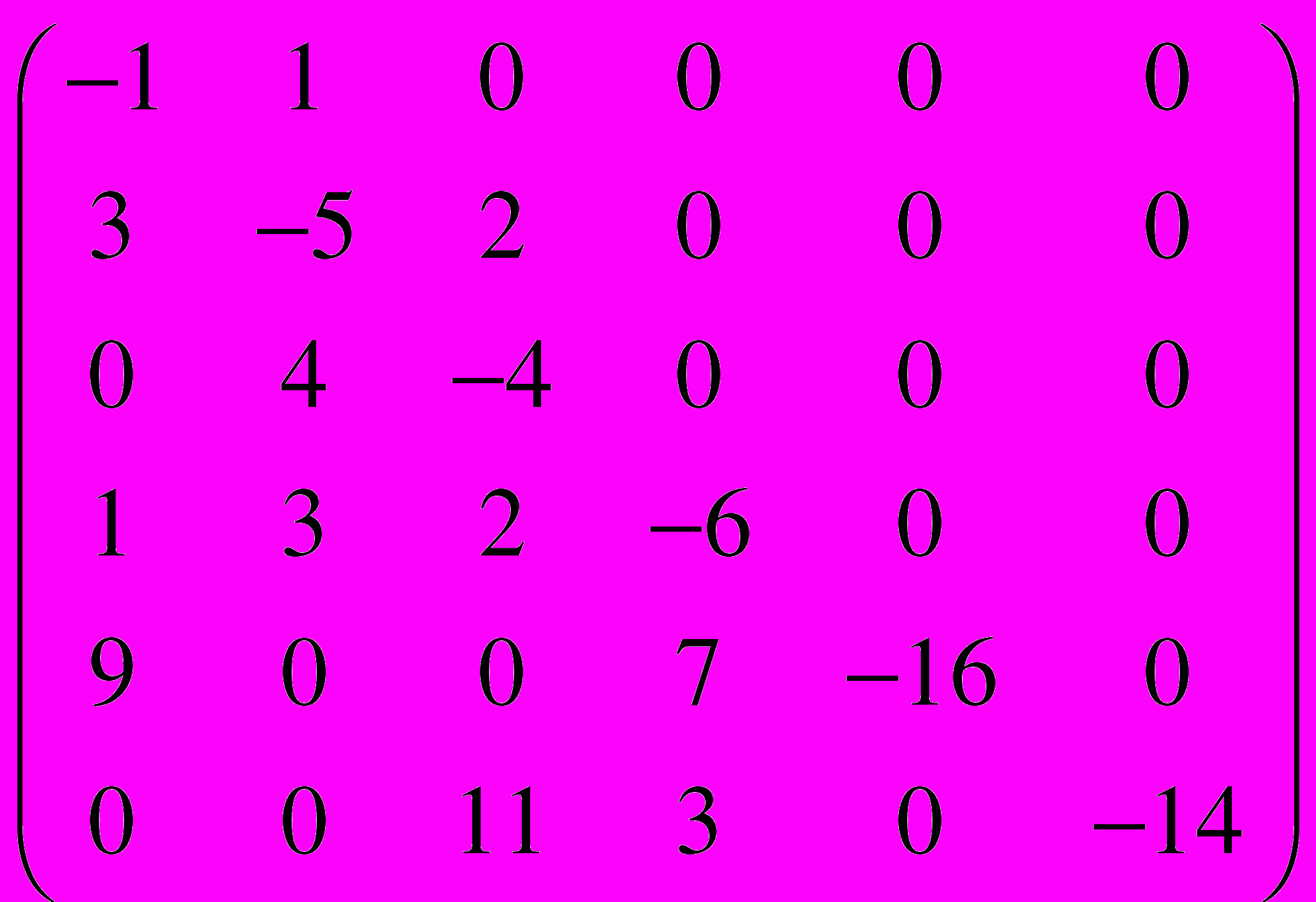32.

.

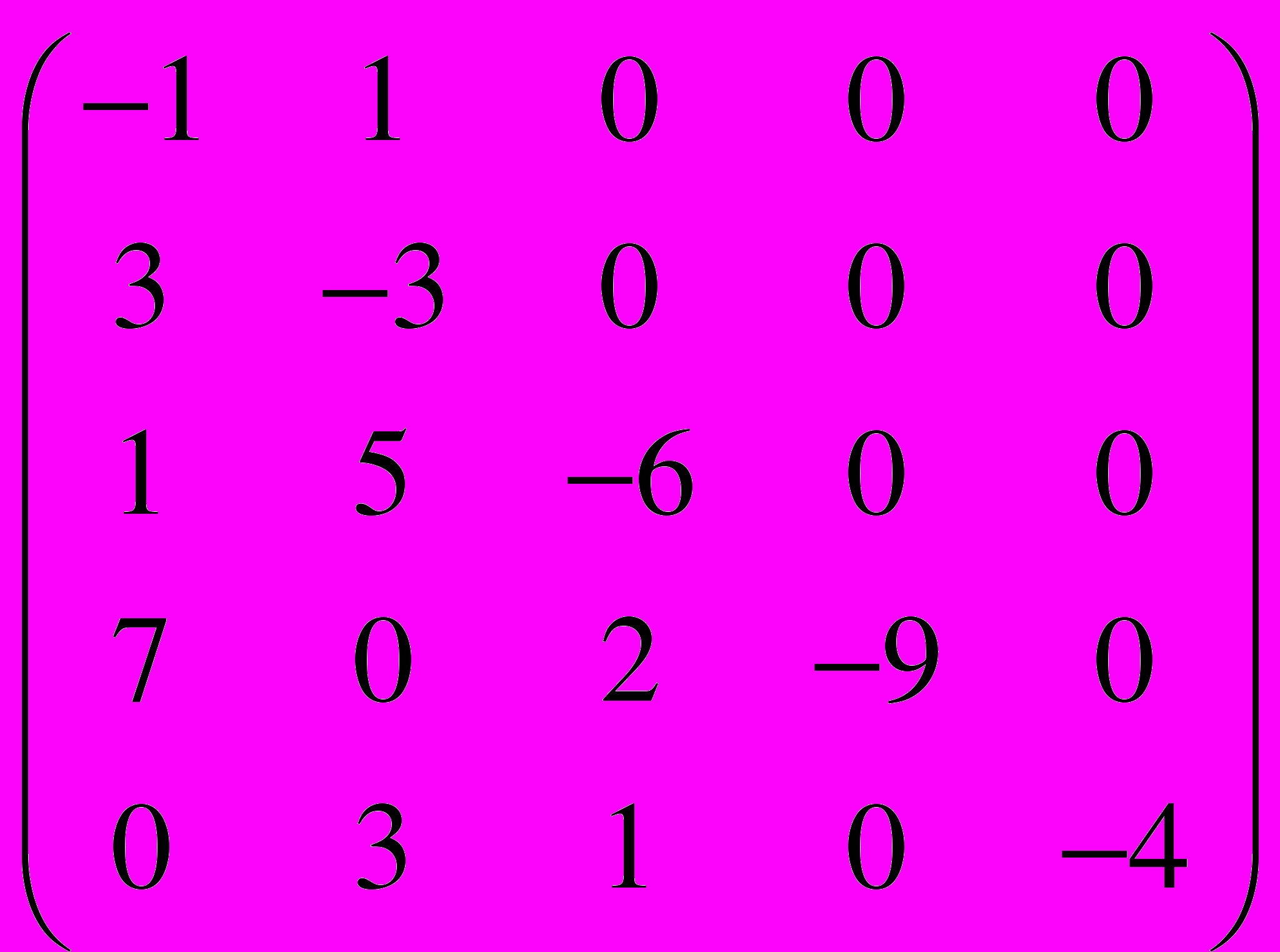33.

.

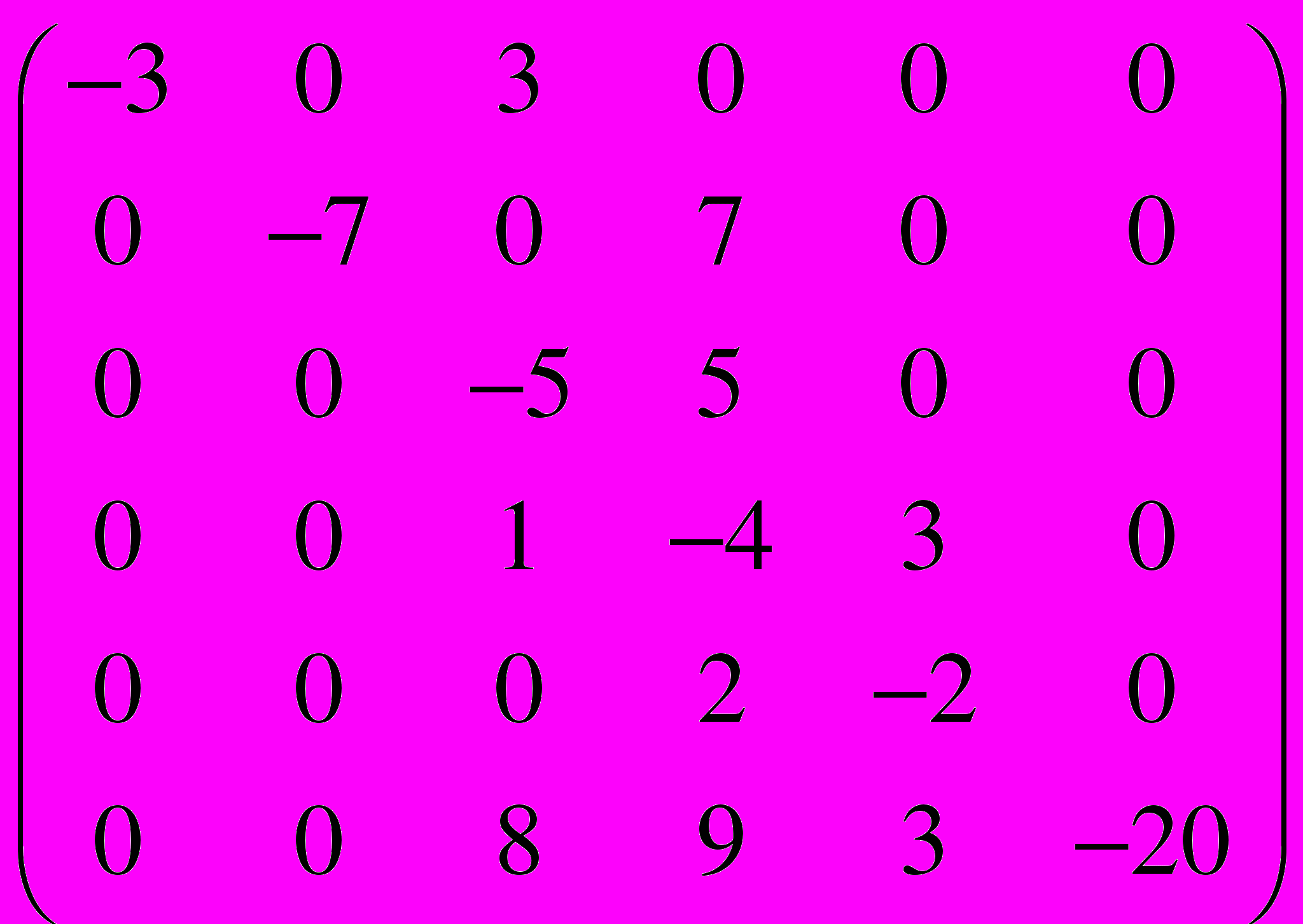34.

.

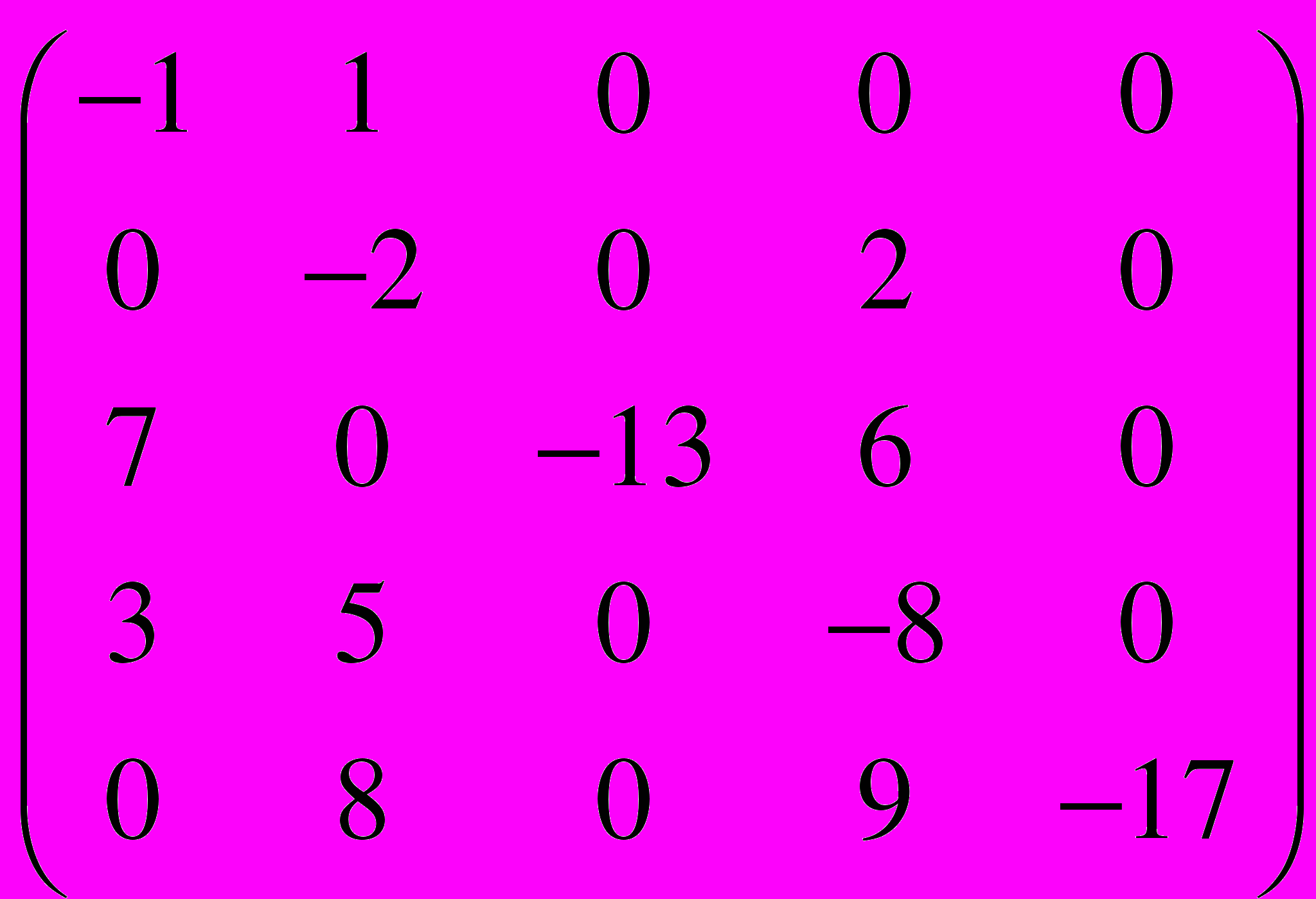35.

.

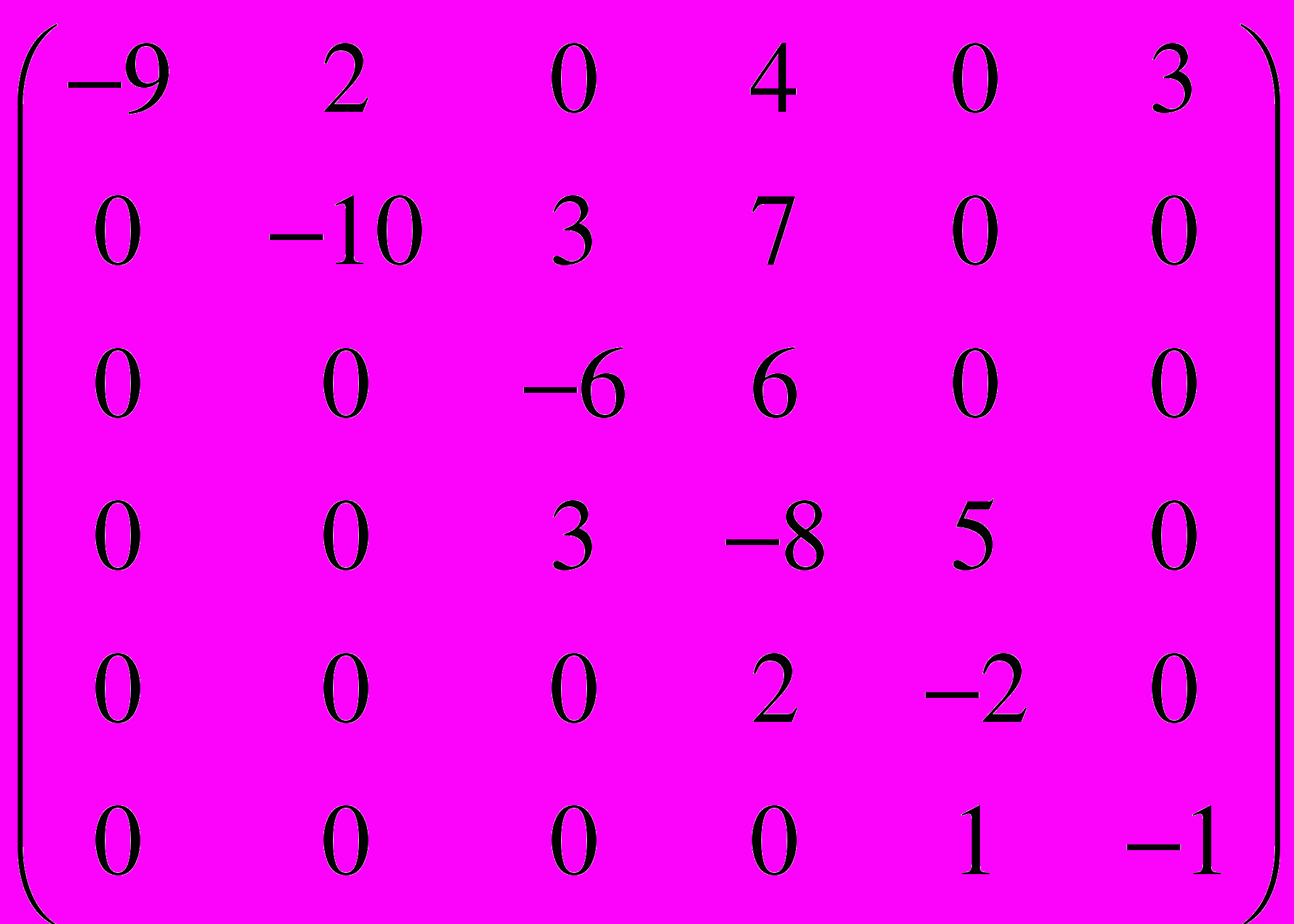36.

.

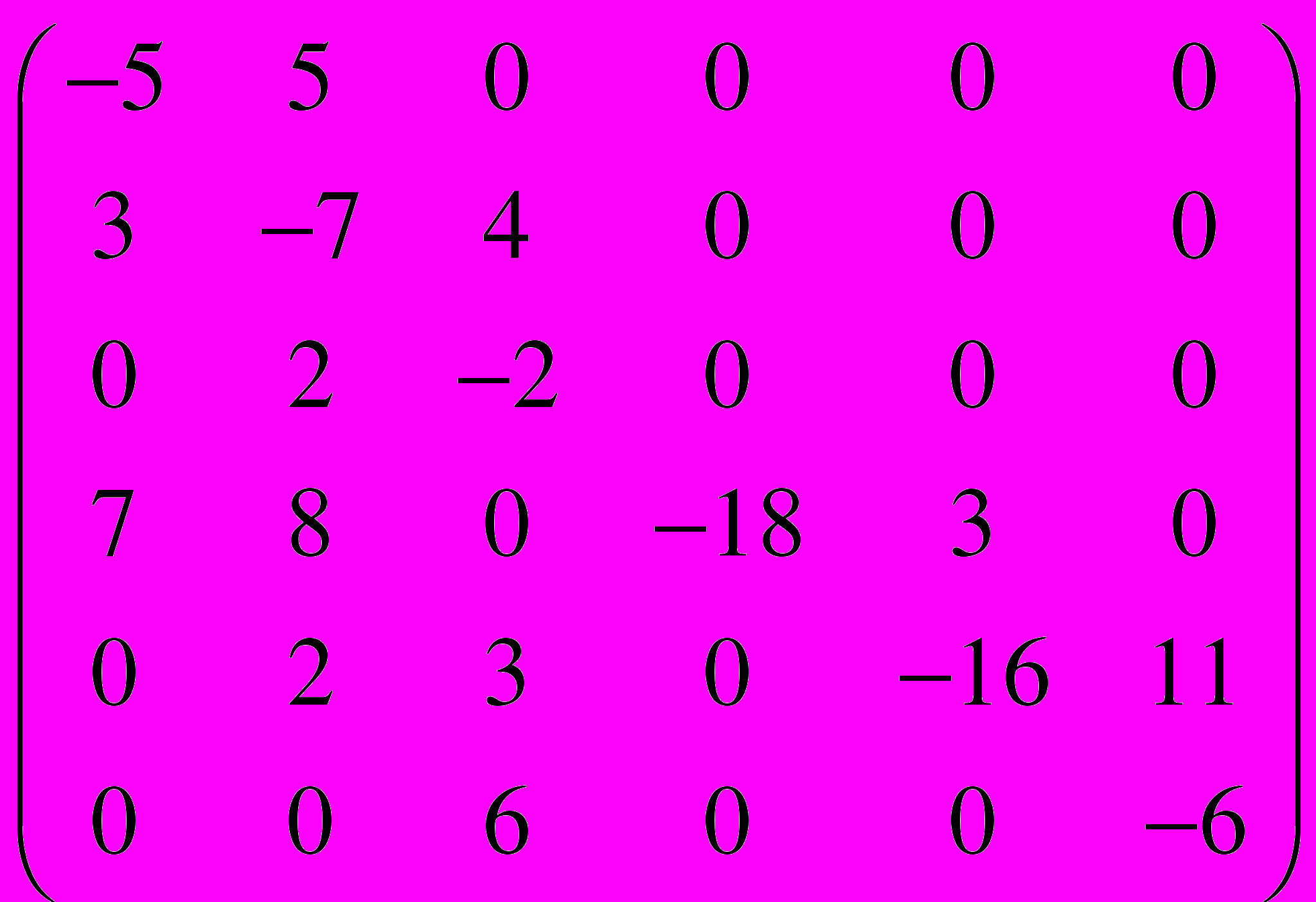37.

.

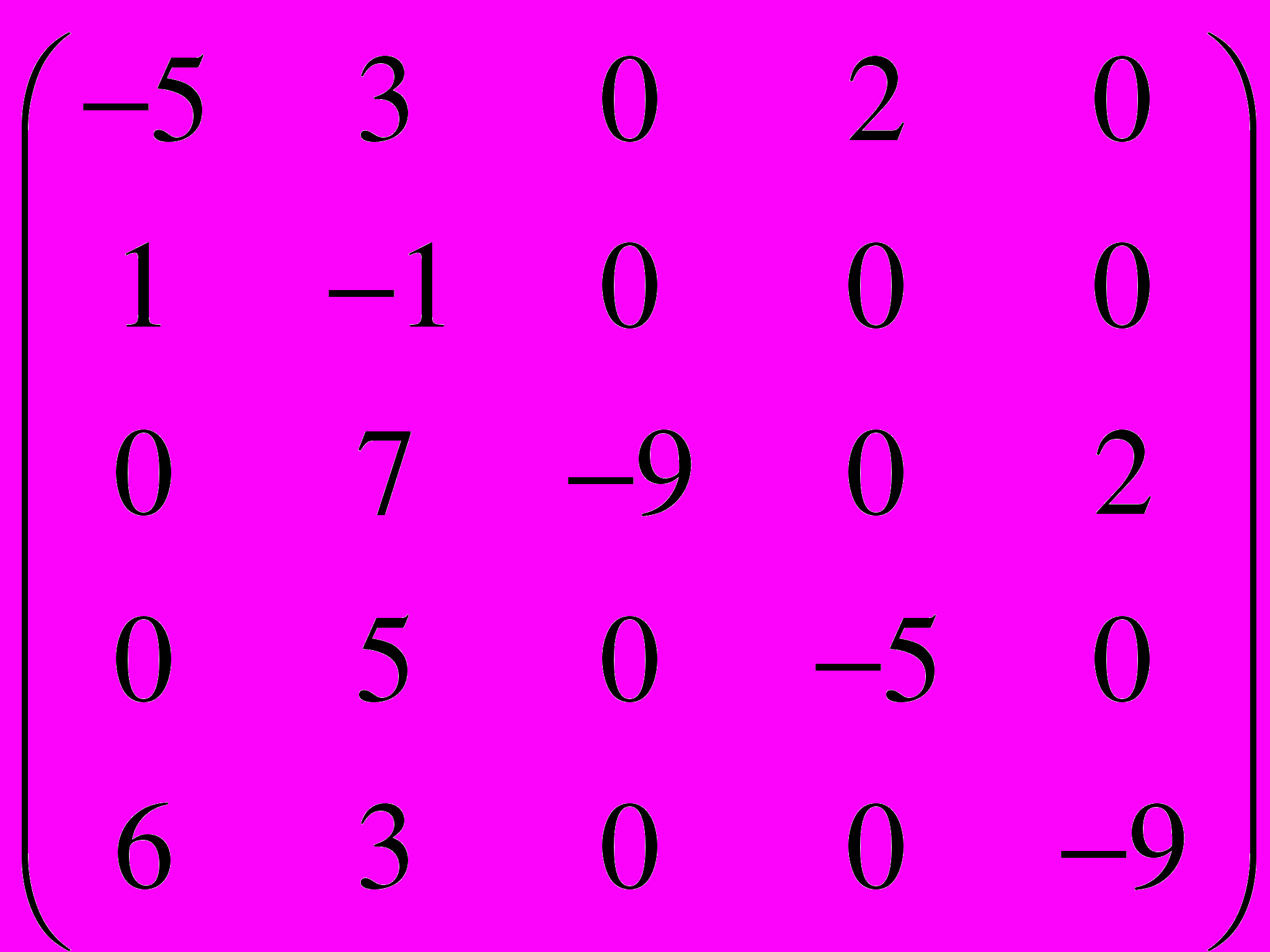38.

.

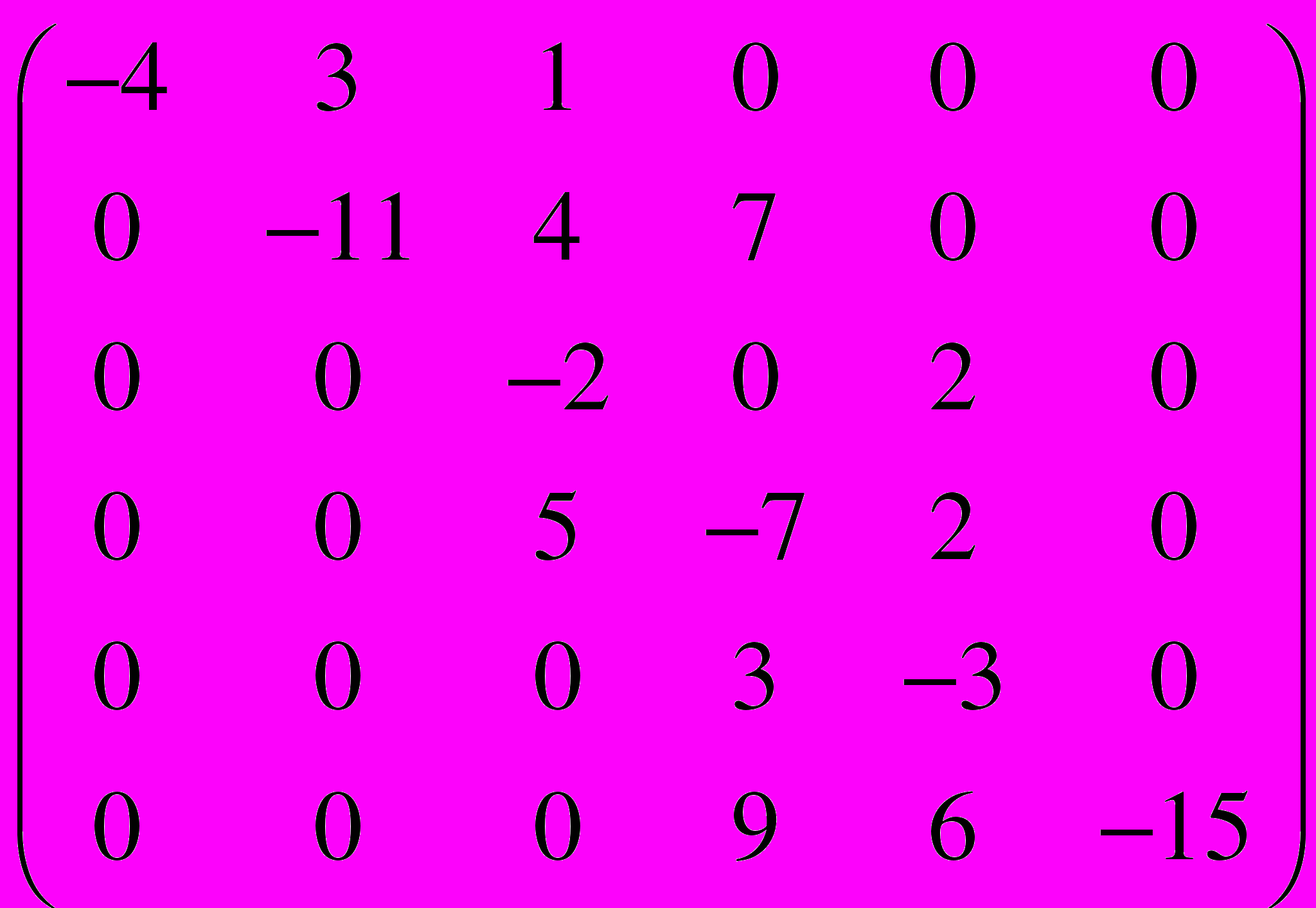39.

.

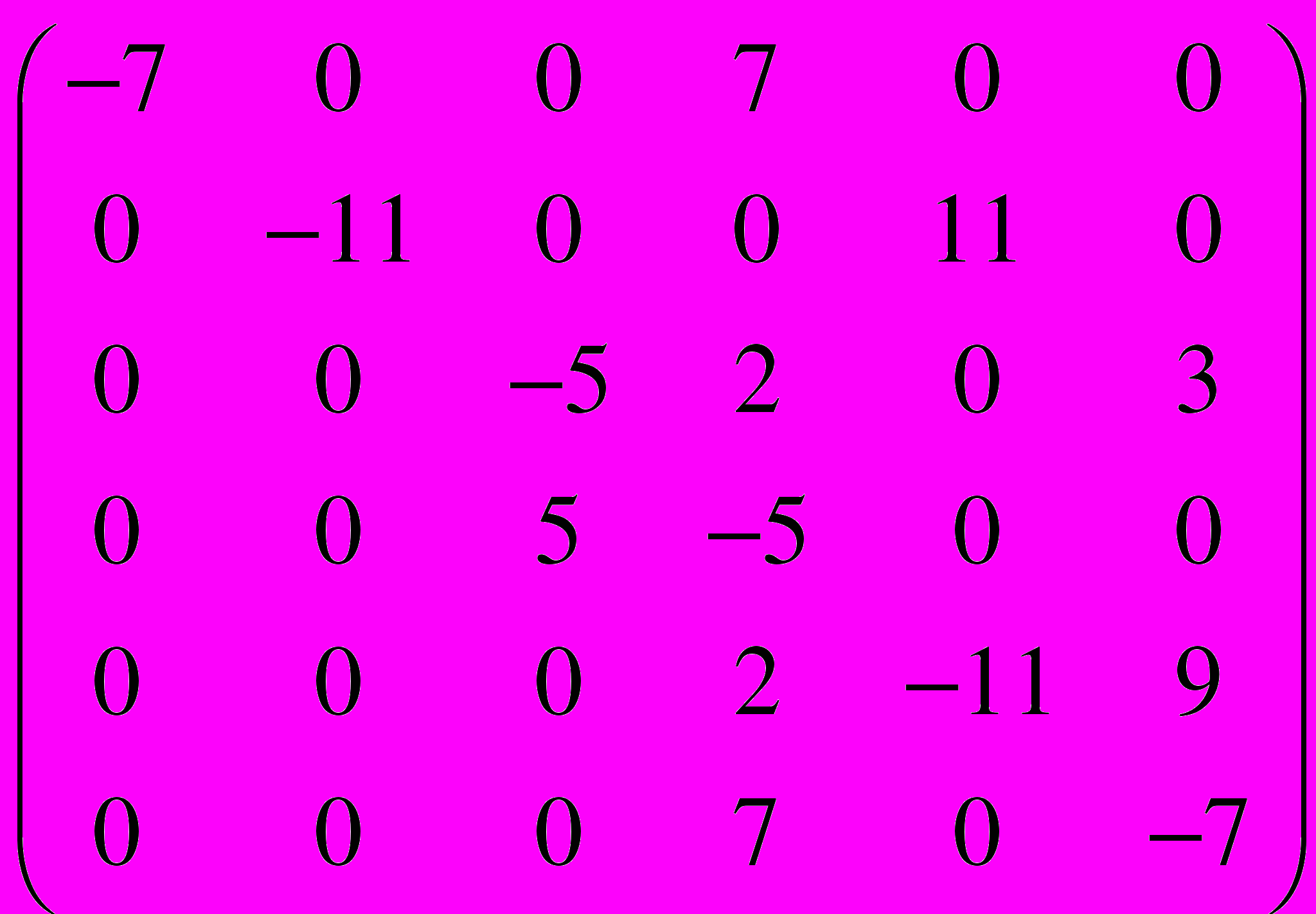40.

.

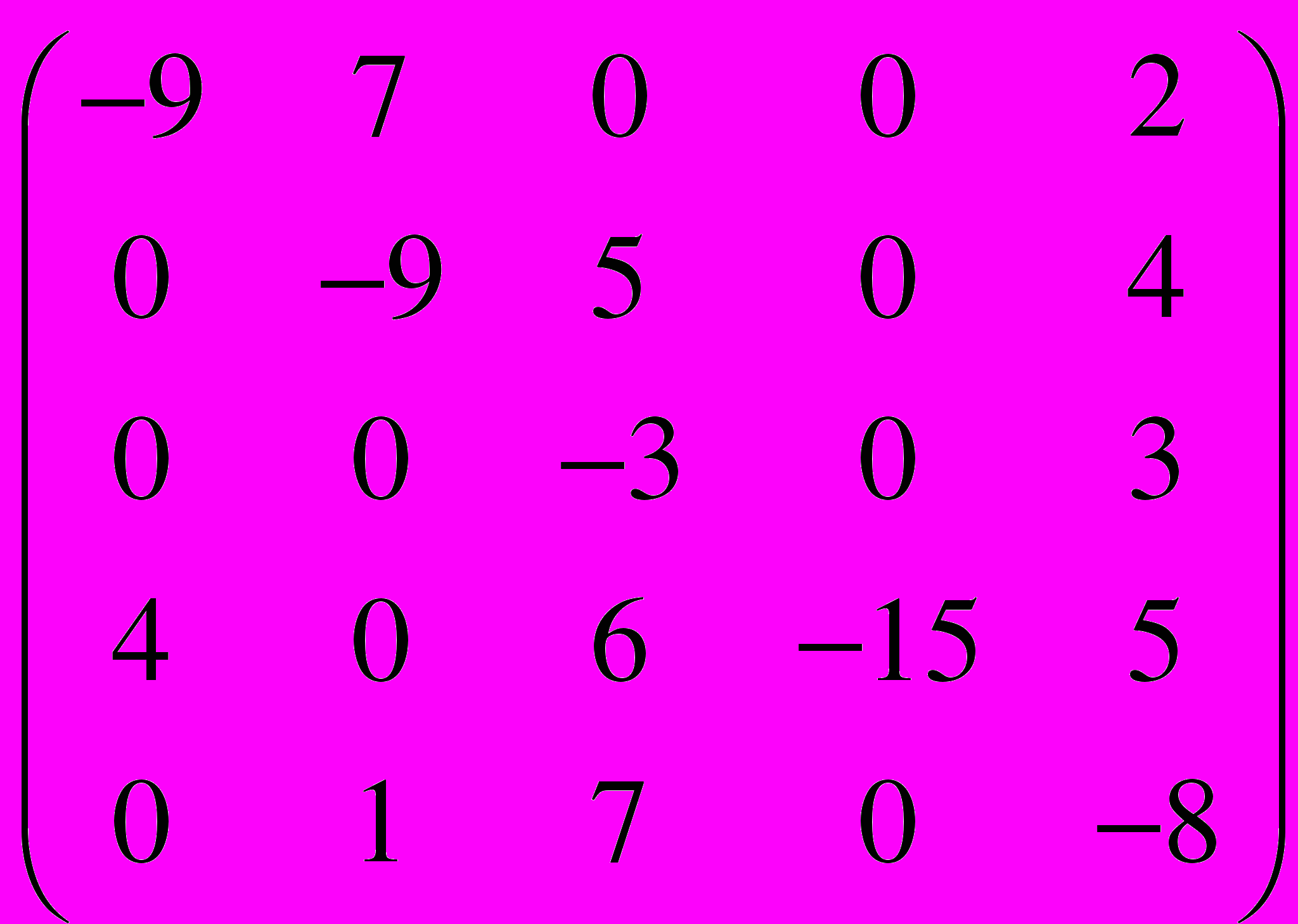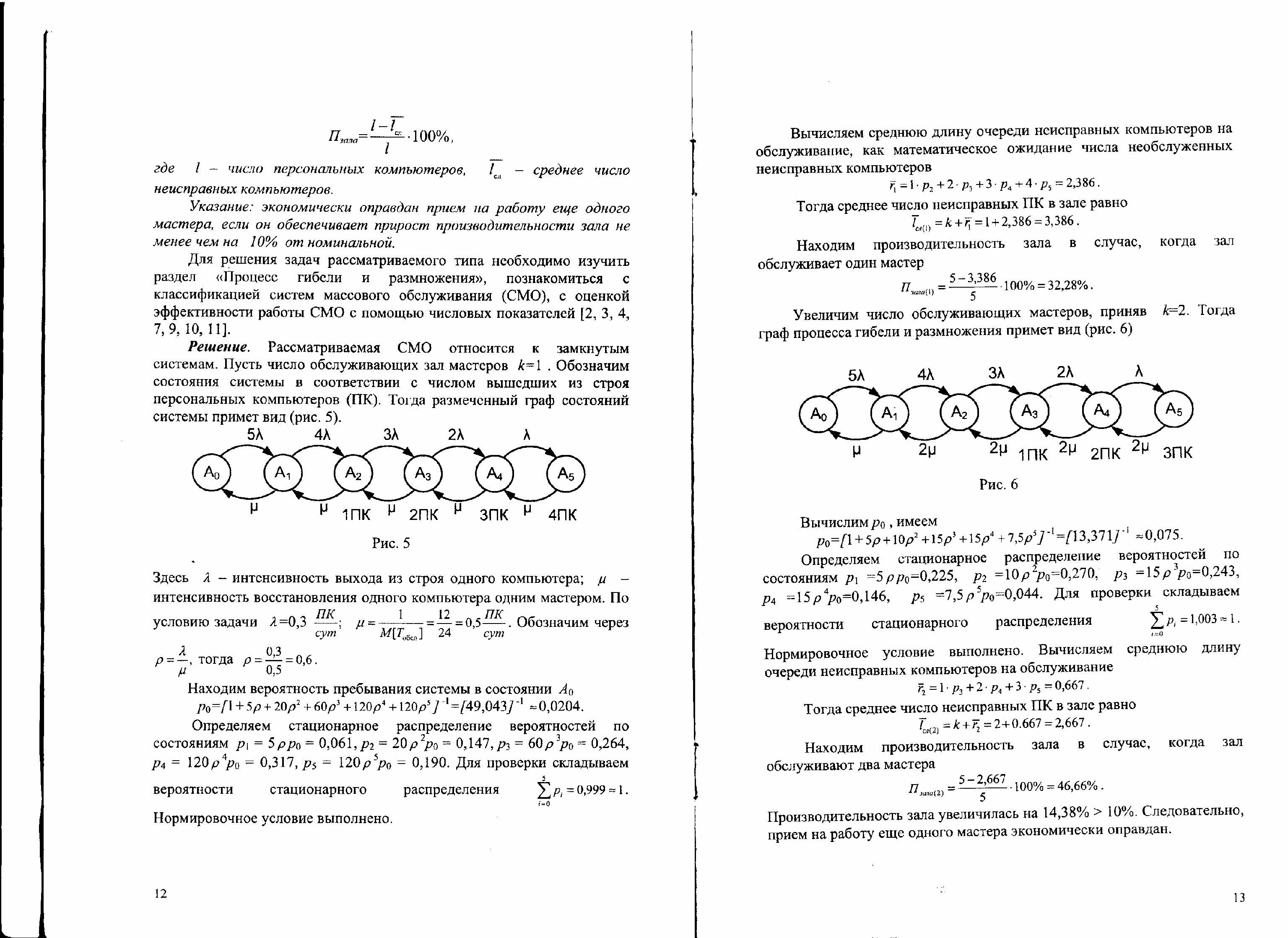
41–50. В компьютерном зале l персональных ком-пьютеров. Зал эксплуатируется 12 часов в сутки. Интенсивность потока отказов одного компьютера равна

компьютеров в сутки. Время восстановления одного компьютера одним мастером в среднем составляет T часов. Все потоки простейшие. Определить оптимальное число обслуживающих зал мастеров по ремонту, если производительность зала оценивается по формуле

П_зала=,

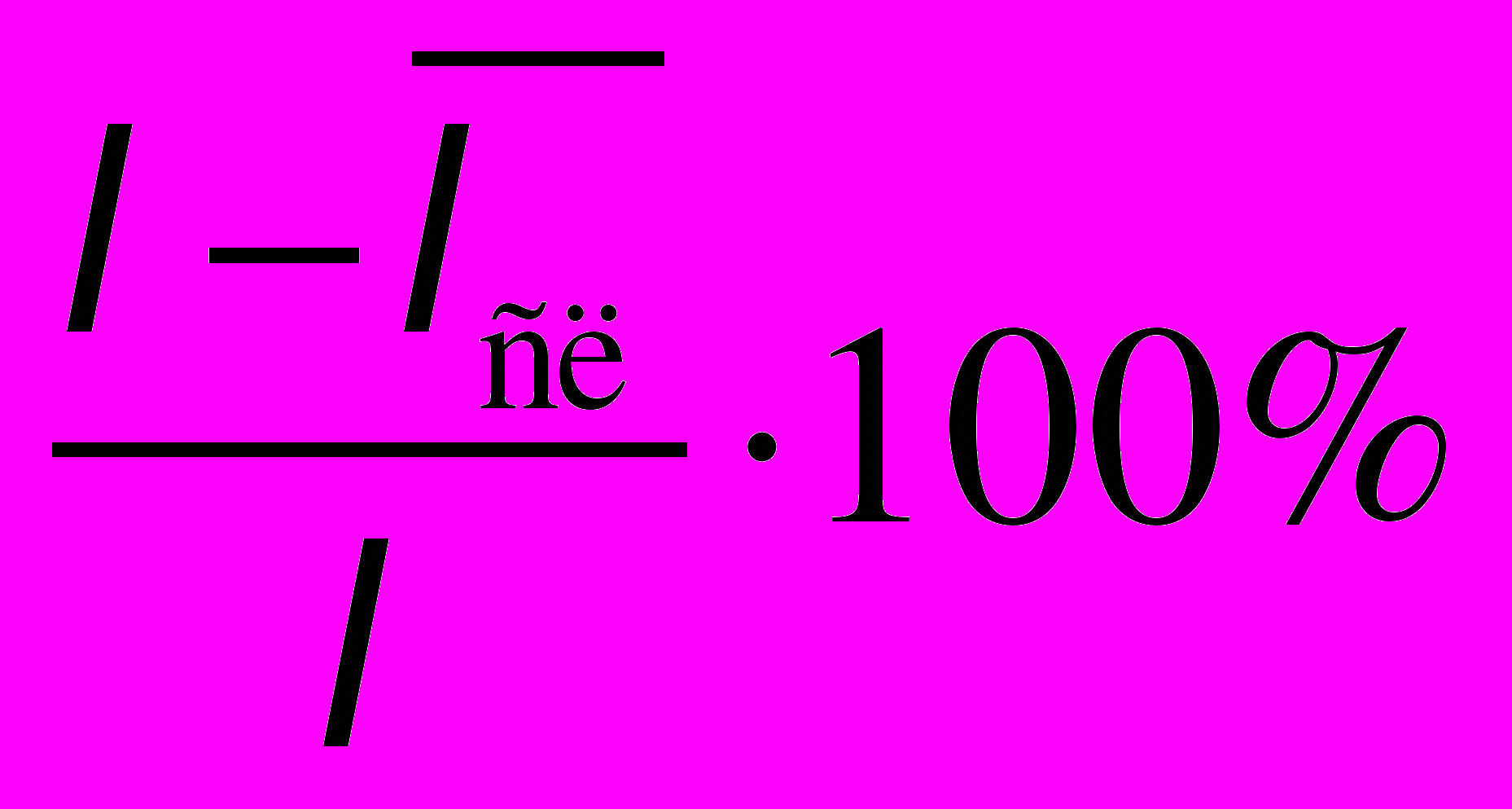где l - число персональных компьютеров,

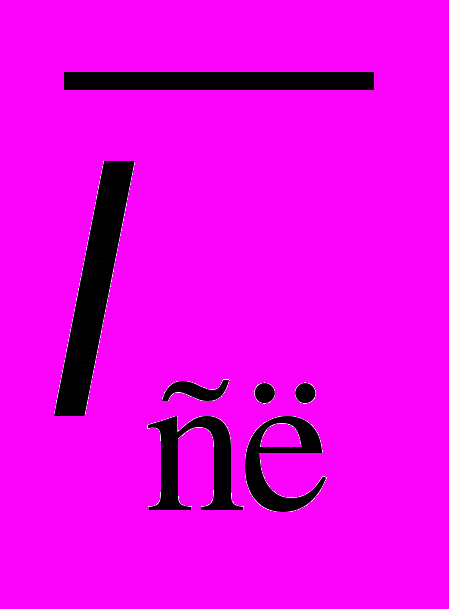- среднее число неисправных компьютеров.

Указание: экономически оправдан прием на работу еще одного мастера, если он обеспечивает прирост производительности зала не менее чем на 10% от номинальной.

41. l = 6,

= 0,2, T = 36.

42. l = 5,

= 0,2, T = 30.

43. l = 4,

= 0,2, T = 24.

44. l = 6,

= 0,15, T = 48.

45. l = 5,

= 0,3, T = 20.

46. l = 4,

= 0,1, T = 48.

47. l = 6,

= 0,3, T = 24.

48. l = 5,

= 0,15, T = 40.

49. l = 4,

= 0,16, T = 30.

50. l = 6,

= 0,24, T = 30.

51–60. В отделе k телефонных аппаратов. Среднее число поступающих в отдел вызовов равно

вызовов в час. Входной поток простейший. Время переговоров распределено по показательному закону и в среднем составляет T минут. Определить: 1) вероятность отказа в переговорах; 2) абсолютную пропускную способность системы; 3) относительную пропускную способность; 4) среднее число занятых аппаратов; 5) коэффициент загрузки оборудования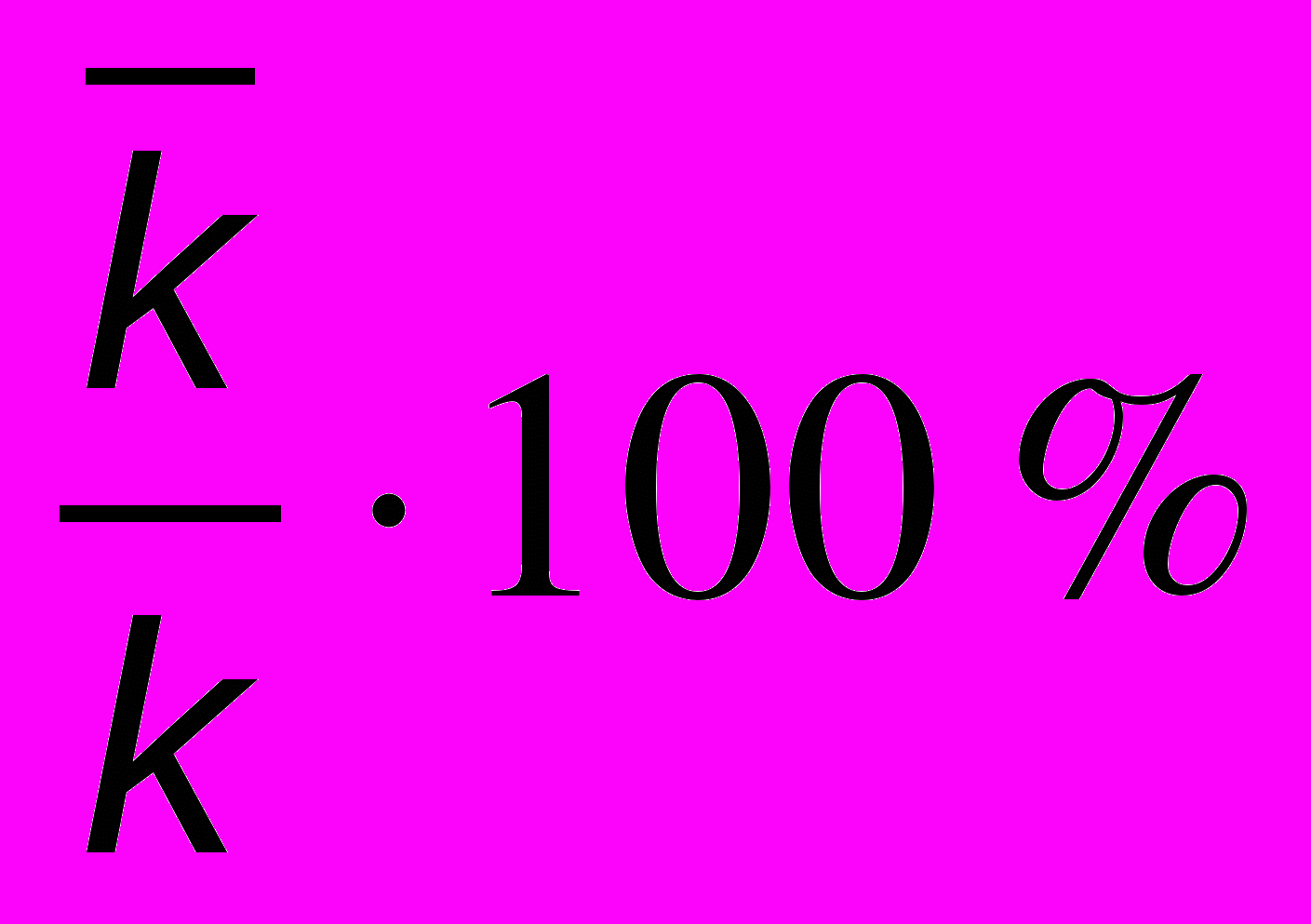

.

Как изменятся эти показатели работы системы, если в отделе добавить еще один аппарат? Сколько аппаратов необходимо добавить, чтобы отказ получали не более 10 % вызовов?

51. k = 3,

= 20, T = 10.

52. k = 2,

= 15, T = 12.

53. k = 2,

= 8, T = 15.

54. k = 3,

= 10, T = 18.

55. k = 2,

= 5, T = 24.

56. k = 4,

= 24, T = 10.

57. k = 3,

= 15, T = 12.

58. k = 4,

= 30, T = 12.

59. k = 2,

= 10, T = 18.

60. k = 3,

= 25, T = 6.

61–70. Разработчик СМО располагает двумя каналами обслуживания. Интенсивность обслуживания одним каналом  заявок в час. Время обслуживания распределено по показательному закону. Входящий поток заявок простейший с интенсивностью  заявок в час. Возможны два варианта проекта: вариант 1 – две независимо работающих одноканальных безотказных СМО( 1;  ; /2 ;  ); вариант 2 – одна двухканальная безотказная СМО( 2 ;  ;  ;  ) . Провести сравнительный анализ вариантов по следующим показателям эффективности: среднее число занятых каналов; средняя длина очереди; среднее время пребывания заявки в системе.

Провести аналогичный сравнительных анализ в том случае, если при тех же условиях разработчик располагает средствами для организации m мест в очереди для ожидания обслуживания. Рассмотреть два варианта: вариант 1 – две независимо работающих одноканальных СМО( 1; m/2 ; /2 ;  ) ; вариант 2 – одна двухканальная СМО( 2 ; m ;  ;  ) .

Указание: всюду вектор ( а₁; а₂; а₃; а₄) имеет компоненты: а₁ – число каналов обслуживания; а₂ – число мест в очереди; а₃ – интенсивность входного потока; а₄ – интенсивность потока обслуживания.

61.  = 8 ,  = 5 , m = 6 .

62.  = 6 ,  = 5 , m = 4.

63.  = 6 ,  = 4 , m = 6 .

64.  = 8 ,  = 7 , m = 4 .

65.  = 10,  = 6 , m = 6 .

66.  = 10,  = 7 , m = 4 .

67.  = 8 ,  = 6 , m = 4 .

68.  = 12,  = 7 , m = 6 .

69.  = 4 ,  = 3 , m = 4 .

70.  = 10,  = 8 , m = 4 .

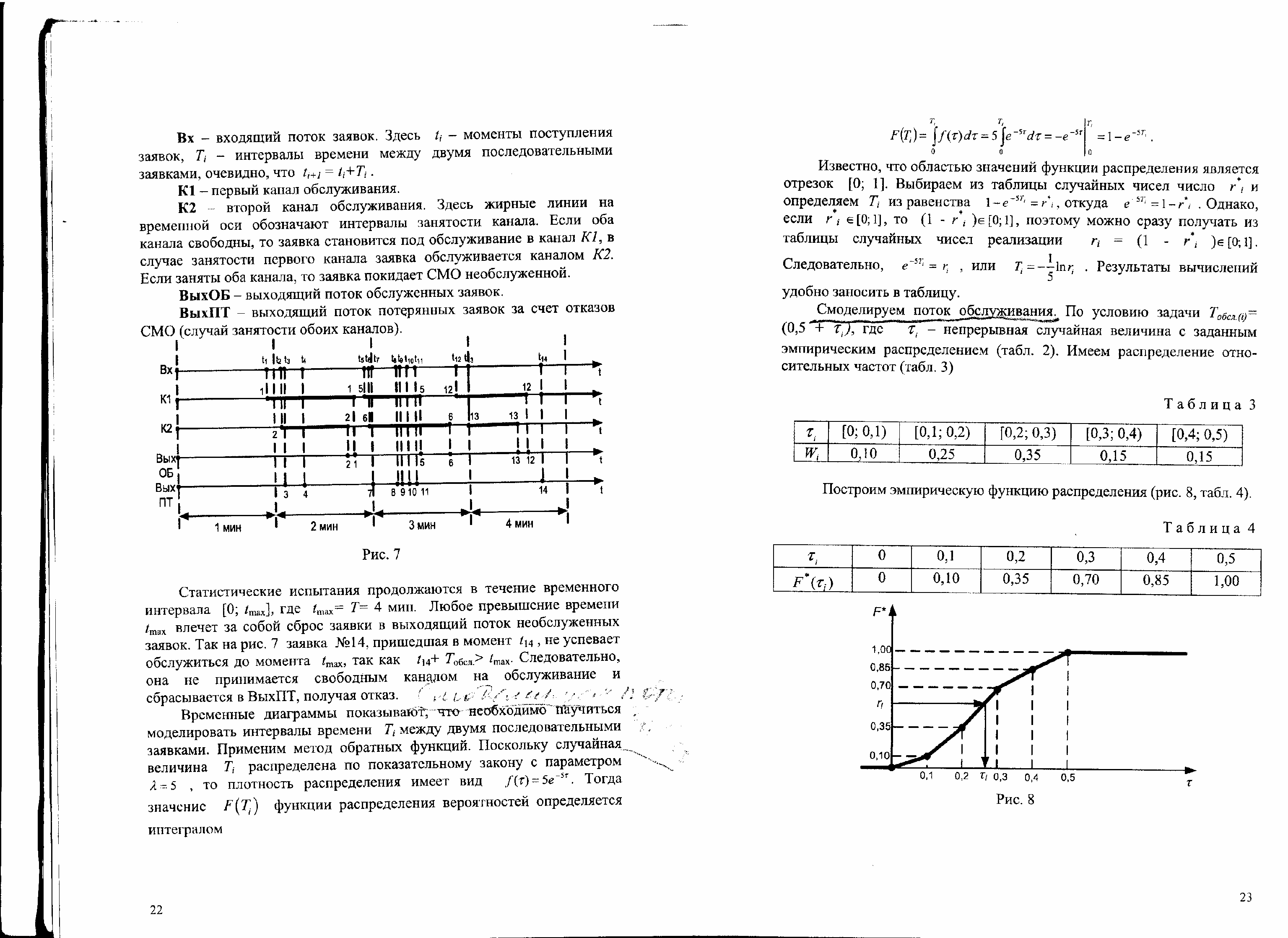
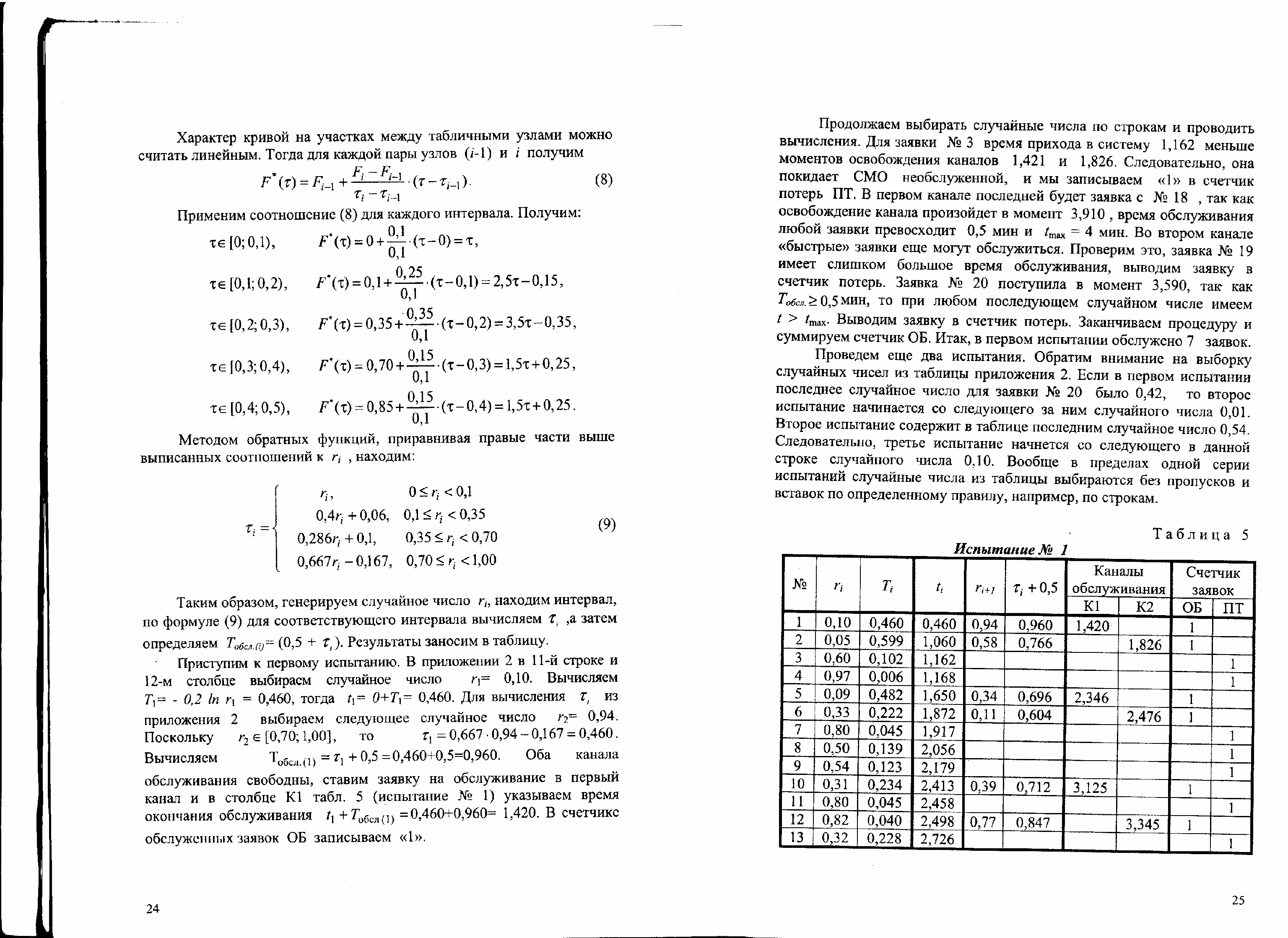
71–80. В двухканальную систему массового обслуживания (СМО) с отказами поступает стационарный пуассоновский поток заявок с интенсивностью

заявок в минуту. Длительность обслуживания каждой заявки равна (0,5 +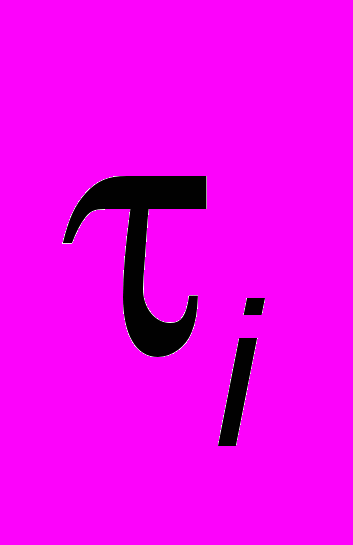

) минут, где

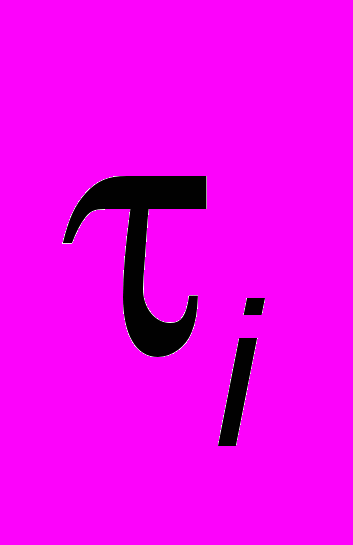– непрерывная случайная величина, закон распределения которой неизвестен. Статистическое распределение выборки {

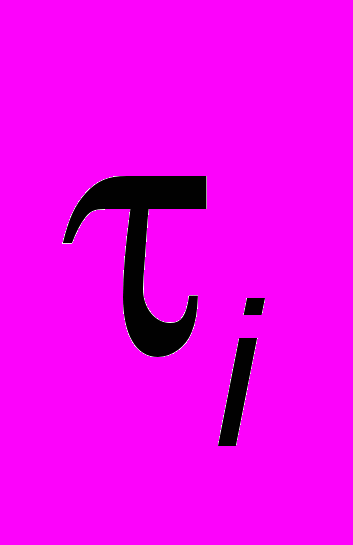} объема n = 100 имеет вид

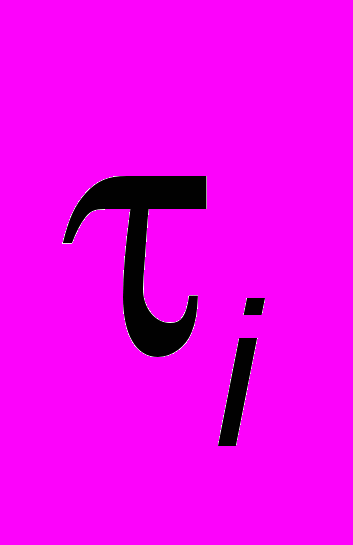,мин	[0; 0,1)	[0,1; 0,2)	[0,2; 0,3)	[0,3; 0,4)	[0,4; 0,5)
n_i	10	25	35	15	15

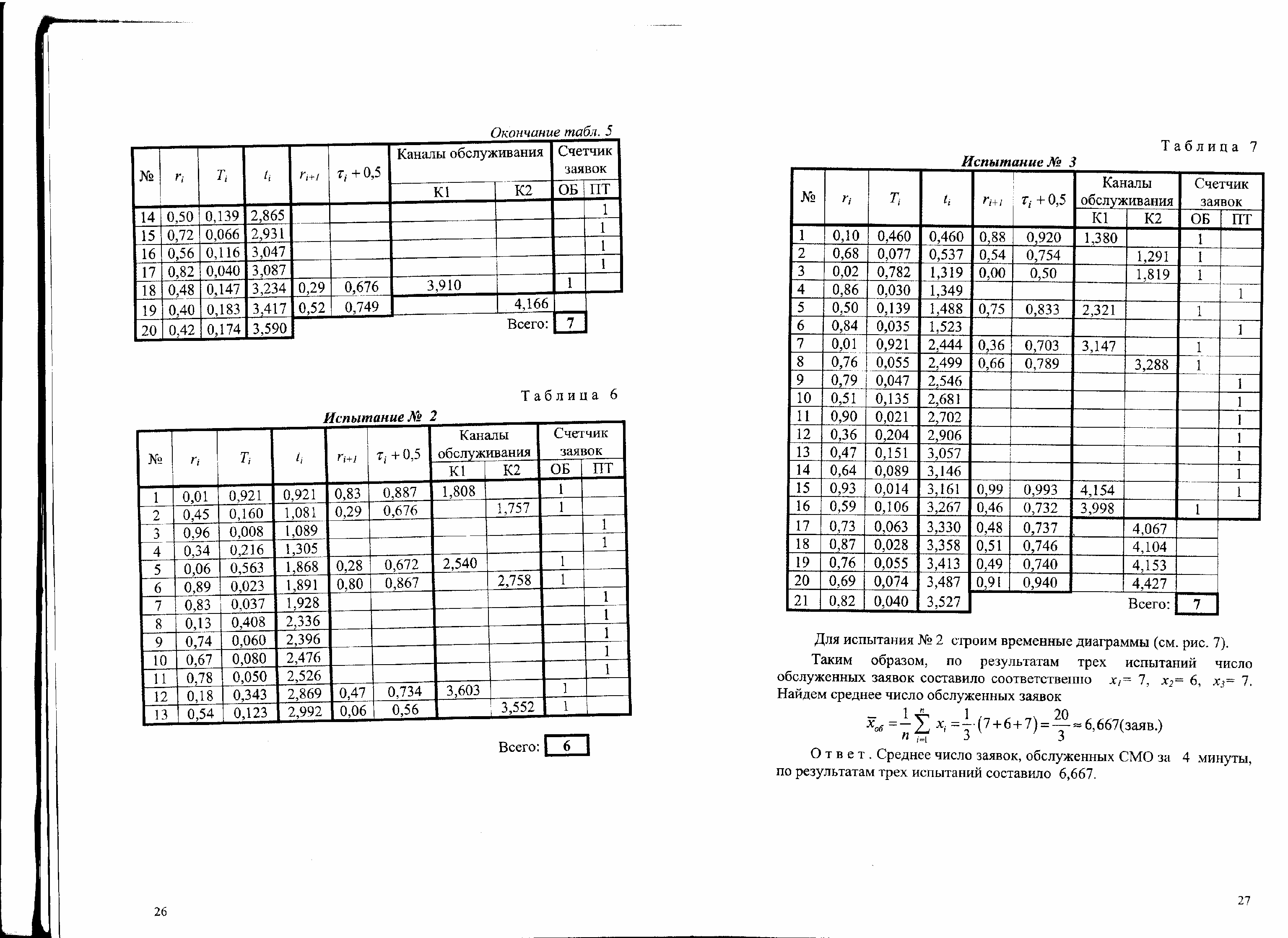
Вновь прибывшая заявка занимает свободный канал с меньшим номером. При занятости всех каналов заявка покидает СМО необслуженной. Требуется: 1) построить эмпирическую функцию распределения случайной величины

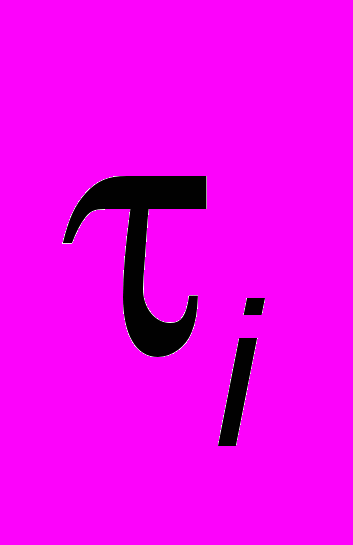; 2) методом обратных функций смоделировать входящий поток и поток обслуживания; 3) смоделировать работу СМО методом Монте-Карло; 4) по результатам трех испытаний найти среднее число обслуженных заявок за время T; 5) к одному из испытаний (любому) построить временные диаграммы работы СМО.

Указание: воспользоваться таблицей случайных чисел, приведенной на стр. 24 – 25. В числовых данных задачи: i – номер строки, j – номер столбца для первого случайного числа r_i_j . Выбор случайных чисел проводить по строкам, начиная с числа r_i_j , без пропусков и вставок.

71. = 2, T = 5, i = 1, j = 2.

72. = 3, T = 4, i = 2, j = 4.

73. = 4, T = 3, i = 3, j = 6.

74. = 5, T = 3, i = 4, j = 8.

75. = 2, T = 6, i = 5, j = 10.

76. = 3, T = 5, i = 6, j = 12.

77. = 4, T = 4, i = 7, j = 14.

78. = 5, T = 4, i = 8, j = 16.

79. = 2, T = 4, i = 9, j = 18.

80. = 3, T = 3, i = 10, j = 20.

8. ЗАЩИТА КОНТРОЛЬНЫХ РАБОТ

После проверки выполненной контрольной работы преподавателем и устранения студентом всех ошибок и недочетов работа допускается к защите. Преподаватель это отмечает на титульном листе, где проставляет дату допуска и свою подпись.

Защиту работы студент проводит по билетам, содержащим два вопроса. Формулировка вопросов и ответы на них фиксируются в конце тетради после подписи преподавателя, удостоверяющей допуск к защите.

9. СДАЧА ЭКЗАМЕНА ПО КУРСУ

После получения зачета по практической части курса студент должен сдать экзамен. Экзамен проводят по билетам, каждый из которых содержит три вопроса: два вопроса теоретических и одна задача. Приведем пример экзаменационного билета и задачи.

БИЛЕТ № 45

Потоки событий. Простейший поток и его свойства.
Одноканальная СМО с неограниченной очередью, простейшим входящим потоком и произвольным распределением времени обслуживания. Формулы Полячека-Хинчина.
Задача 45.

Задача 45

Переговорный пункт имеет четыре линии связи. Поток вызовов простейший с интенсивностью 0,7 вызовов в минуту. Среднее время переговоров составляет 2,7 минуты и распределено по показательному закону. Найти абсолютную и относительную пропускную способность, вероятность отказа в переговорах.

Заочная форма обучения

Преп. _______________

Т Е Т Р А Д Ь

для контрольной работы

по дисциплине

«Теория массового обслуживания»

студента(ки) __третьего ___курса

факультета ___ УПП____

специальности ____ЭВМ _____

_Григорьевой_________________

_Елены Николаевны__________

(Ф.И.О. студента полностью)

Шифр: 0710 – п/ЭВМ - 3578

Допущено к защите _______________

Дата ____________________________

Зачтено__________________________

Дата ____________________________

РОАТ

Москва – 2009

Приложение 1

Приложение 2

СЛУЧАЙНЫЕ ЧИСЛА

10 09 73 25 33 76 52 01 35 86 34 67 35 48 76 80 95 90 91 17

37 54 20 48 05 64 89 47 42 96 24 80 52 40 37 20 63 61 04 02
08 42 26 89 53 19 64 50 93 03 23 20 90 25 60 15 95 33 47 64
99 01 90 25 29 09 37 67 07 15 38 31 13 11 65 88 67 67 43 97

12 80 79 99 70 80 15 73 61 47 64 03 23 66 53 98 95 11 68 77

66 06 57 47 17 34 07 27 68 50 36 69 73 61 70 65 81 33 98 85

31 06 01 08 05 45 57 18 24 06 35 30 34 26 14 86 79 90 74 39

85 26 97 76 02 02 05 16 56 92 68 66 57 48 18 73 05 38 52 47

63 57 33 21 35 05 32 54 70 48 90 55 35 75 48 28 46 82 87 09

73 79 64 57 53 03 52 96 47 78 35 80 83 42 82 60 93 52 03 44

65 48 11 76 74 17 46 85 09 50 58 04 77 69 74 73 03 95 71 86

80 12 43 56 35 17 72 70 80 15 45 31 82 23 74 21 11 57 82 53

74 35 29 98 17 77 40 27 72 14 43 23 60 02 10 45 52 16 42 37

69 91 62 68 03 66 25 22 91 48 36 93 68 72 03 76 62 11 39 90

09 89 32 05 05 14 22 56 85 14 46 42 75 67 88 96 29 77 88 22

91 49 91 45 23 68 47 92 76 86 46 16 28 35 54 94 75 08 99 23

80 33 69 45 98 26 94 03 68 58 70 29 73 41 35 53 14 03 33 40

44 10 48 19 49 85 15 74 79 54 32 97 92 65 75 57 60 04 08 81

12 55 07 37 42 11 10 00 20 40 12 86 07 46 97 96 64 48 94 39

63 60 64 93 29 16 50 53 44 84 40 21 95 25 63 43 65 17 70 82

61 19 69 04 46 26 45 74 77 74 51 92 43 37 29 65 39 45 95 93

15 47 44 52 66 95 27 07 99 53 59 36 78 38 48 82 39 61 01 18

94 55 72 85 73 67 89 75 43 87 54 62 24 44 31 91 19 04 25 92

42 48 11 62 13 97 34 40 87 21 16 86 84 87 67 03 07 11 20 59

23 52 37 83 17 73 20 88 98 37 68 93 59 14 16 26 25 22 96 63

04 49 35 24 94 75 24 63 38 24 45 86 25 10 25 61 96 27 93 35

00 54 99 76 54 64 05 18 81 59 96 11 96 38 96 54 69 28 23 91

35 96 31 53 07 26 89 80 93 54 33 35 13 54 62 77 97 45 00 24

59 80 80 83 91 45 42 72 68 42 83 60 94 97 00 13 02 12 48 92

46 05 88 52 36 01 39 09 22 86 77 28 14 40 77 93 91 08 36 47

32 17 90 05 97 87 37 92 52 41 05 56 70 70 07 86 74 31 71 57

69 23 46 14 06 20 11 74 52 04 15 95 66 00 00 18 74 39 24 23

19 56 54 14 30 01 75 87 53 79 40 41 92 15 85 66 67 43 68 06

45 15 51 49 38 19 47 60 72 46 43 66 79 45 43 59 04 79 00 33

94 86 43 19 94 36 16 81 08 51 34 88 88 15 53 01 54 03 54 56

98 08 62 48 26 45 24 02 84 04 44 99 90 88 96 39 09 47 34 07

33 18 51 62 32 41 94 15 09 49 89 43 54 85 81 88 69 54 19 94

80 95 10 04 06 96 38 27 07 74 20 15 12 33 87 25 01 62 52 98

79 75 24 91 40 71 96 12 82 96 69 86 10 25 91 74 85 22 05 39

18 63 33 25 37 98 14 50 65 71 31 01 02 46 74 05 45 56 14 27

74 02 94 39 02 77 55 73 22 70 97 79 01 71 19 52 52 75 80 21

54 17 84 56 11 80 99 33 71 43 05 33 51 29 69 56 12 71 92 55

11 66 44 98 83 52 07 98 48 27 59 38 17 15 39 09 97 33 34 40

48 32 47 79 28 31 24 96 47 10 02 29 53 68 70 32 30 75 75 46

69 07 49 41 38 87 63 79 19 76 35 58 40 44 01 10 51 82 16 15

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ДЛЯ СТУДЕНТОВ

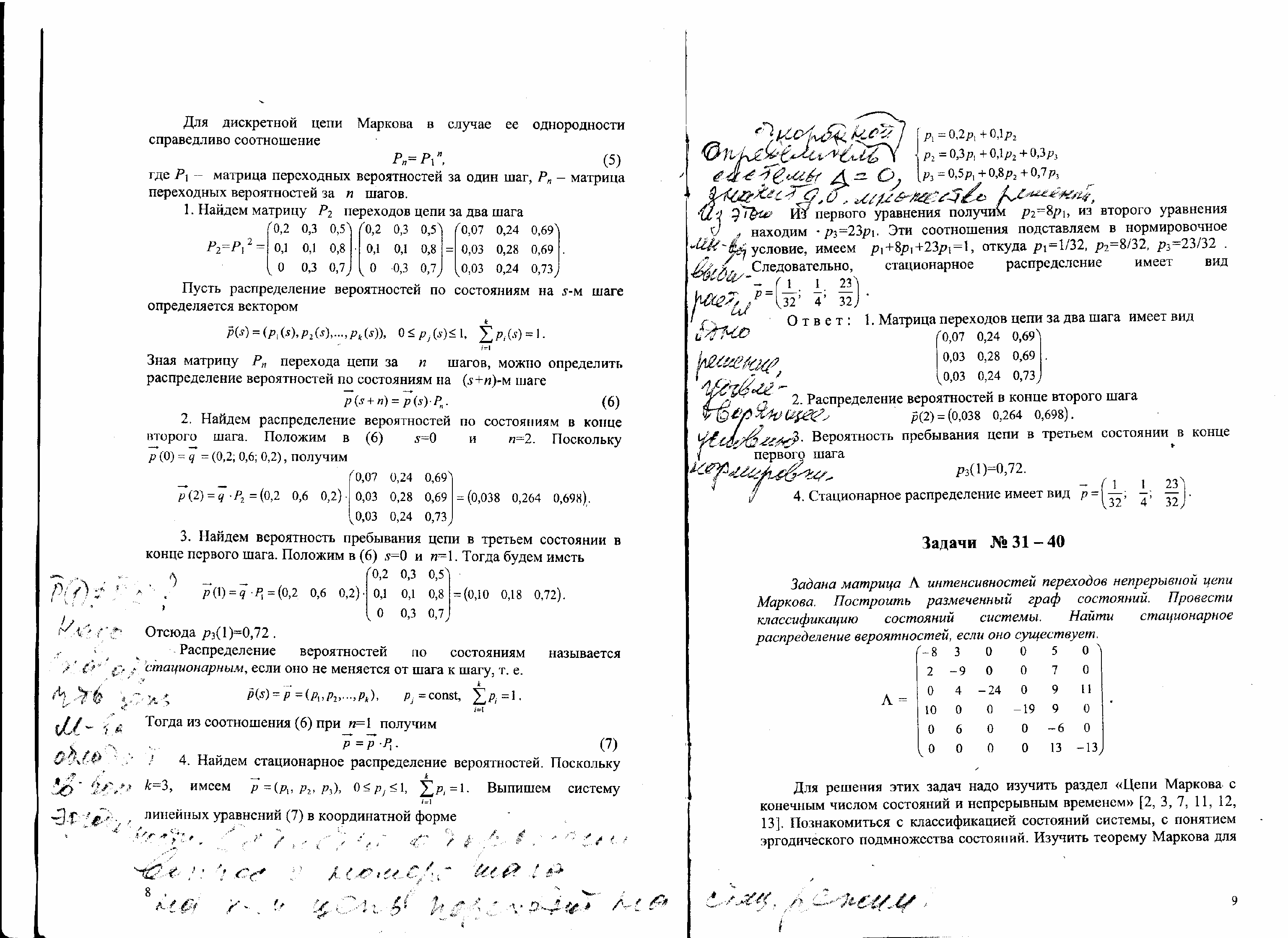
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ДЛЯ ПРЕПОДАВАТЕЛЕЙ

Основной объем учебной работы студент выполняет самостоятельно, изучая рекомендуемую литературу, в соответствии с учебным материалом рабочей программы, выполняя контрольную работу и подготовку к сдаче зачета по контрольной работе и экзамена по курсу дисциплины, предусмотренные учебным планом. Контрольная работа состоит из двух задач. Вариант задания на задачу 1 выбирается по предпоследней и последней цифрам студенческого шифра, на задачу 2 – по последней цифре. При необходимости студент консультируется у преподавателя. Лекционные и практические занятия в вузе во время учебной сессии являются установочными.

В процессе обучения рекомендуется использовать современные версии пакетов прикладных программ для математических расчетов: Mathematica, Matlab,Mathcad, Maple,Derive, Excel,Statistica. Применение компьютерной техники и прикладных программ имеет целью сокращение времени выполнения расчетов и оформления полученных результатов, но

не может заменить изучение и освоение метода решения задач. Поэтому задачи и необходимые примеры с выполнением всех промежуточных расчетов предварительно решаются вручную и лишь затем, при необходимости использовать освоенные методы и будучи уверенным в правильности их применения и получения ожидаемых результатов, в целях сокращения времени на рутинную работу применяется быстродействующая вычислительная техника.

МАТЕРИАЛЫ ТЕКУЩЕГО, ПРОМЕЖУТОЧНОГО, ИТОГОВОГО КОНТРОЛЯ

Пример экзаменационных билета и задачи

После получения зачета по практической части курса студент должен сдать экзамен. Экзамен проводят по билетам, каждый из которых содержит три вопроса: два вопроса теоретических и одна задача. Приведем пример экзаменационного билета и задачи.

БИЛЕТ № 45

Потоки событий. Простейший поток и его свойства.
Одноканальная СМО с неограниченной очередью, простейшим входящим потоком и произвольным распределением времени обслуживания. Формулы Полячека-Хинчина.
Задача 45.

Blog

Содержание

2. ТРЕБОВАНИЯ К УРОВНЮ ОСВОЕНИЯ

Основная

Дополнительная

БИЛЕТ № 45

Задача 45

БИЛЕТ № 45

Задача 45