Т. С. Рамазанов доктор физико-математических наук, профессор, Казну им. Аль-Фараби, г. Алматы; > С. К. Тлеукенов доктор физико-математических наук, профессор, пгу им. С. Торайгырова, г. Павлодар; > А. М. Мубараков
| Вид материала | Учебник |
Содержание1.1.2 Скорость и ускорение произвольно движущейся точки |
- Титульный лист программы Форма обучения по дисциплине ф со пгу 18. 3/37 (Syllabus), 349.17kb.
- Б. А. – доктор юридических наук, профессор Казну им аль-Фараби, 209.21kb.
- Карпухин В. Б., доктор физико-математических наук, профессор кафедры «Высшая и прикладная, 263.95kb.
- А. М. Мубараков доктор пед наук, профессор. Н. Э. Пфейфер доктор пед наук, профессор, 1066.25kb.
- Веселаго Виктор Георгиевич, доктор физико-математических наук, профессор мфти, область, 30.58kb.
- Практических: 0 Лабораторных, 16.69kb.
- Практических: 34 Лабораторных, 24.5kb.
- Практических: 0 Лабораторных, 16.63kb.
- Практических: 34 Лабораторных, 20.05kb.
- Практических: 0 Лабораторных, 18.53kb.
1.1.2 Скорость и ускорение произвольно движущейся точки
Траектория и перемещение являются лишь чисто геометрическими характеристиками движения. Два различных движения, для которых одно и то же перемещение ∆r совершилось за разные промежутки времени, геометрически одинаковы, но кинематически совершенно различны. Это различие характеризуется быстротой изменения положения точки в пространстве, определяемой отношением
| ∆r/∆t = vср | (1.4) |
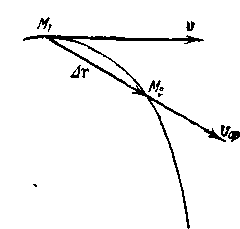
Вектор vcp называется средней скоростью движения точки за время ∆t. Его численное значение |vcp| = | ∆r|/∆t есть скорость такого равномерного и прямолинейного движения, при котором точка М перешла бы из положения М1 в положение М2 за тот же промежуток времени ∆t, за который произошло ее истинное криволинейное движение по дуге M1M2 (рисунок - 1.3). Вектор vcp как и вектор ∆r, направлен по секущей M1M2.
Переходя к пределу для бесконечно малого промежутка времени (∆t →0), мы получим вектор истинной, или мгновенной скорости в точке M1:
| vмгн= lim vcp= lim|∆r|/∆t = dr/dt. | (1.5) |
Поскольку секущая в пределе совпадает с касательной, то вектор скорости v направлен по касательной к траектории (рисунок - 1.3). Тогда согласно (1.3)
| | vмгн| = v = lim|∆S|/∆t = dS/dt | (1.6) |
т. е. величина скорости vмгн численно равна пределу отношения длины пути к промежутку времени, в течение которого это движение произошло. Математически этот предел приводит к понятию производной: мгновенная скорость вычисляется как первая производная от уравнения движения тела.
При прямолинейном движении быстрота изменения величины скорости v характеризуется ускорением а, которая характеризует те изменения скорости, которые произойдут за единицу времени.
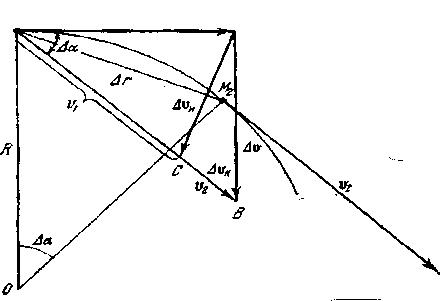
На рисунке - 1.3 изображен отрезок траектории между двумя соседними бесконечно близкими точками М1 и М2. Скорости в этих точках v1 и v2 направлены по касательным к траектории и отличаются друг от друга по величине и по направлению. Перенесем вектор v2 параллельно самому себе в точку М1 как это показано на рисунке 1.4.
 |  |
| Рисунок - 1.3 | Рисунок - 1.4 |
Соединим теперь конец вектора v1 с концом перенесенного вектора v2 вектором ∆v. Из чертежа видно, что ∆v = v2 —vl, т. е. вектор ∆v есть геометрическое приращение вектора v за время ∆t. Отношение
| ∆v/∆t =aср | (1.7) |
является вектором среднего ускорения за время ∆t, а предел этого отношения будет вектором истинного, или мгновенного ускорения
| а = im аcp= lim ∆v/∆t = dv/dt | (1.8). |
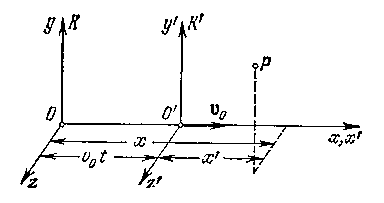
Рассмотрим две системы отсчета, движущиеся друг относительно друга с постоянной скоростью v0. Одну из этих систем, обозначенную на рисунке 1.6 буквой К будем условно считать неподвижной. Тогда вторая система К' будет двигаться прямолинейно и равномерно. Выберем координатные оси х, у, z системы К и оси х' , у', z' системы К' так, чтобы оси х и х' совпадали, а оси у н у', а также z и z' были параллельны друг другу. Найдем связь между координатами x, у, z некоторой точки Р в системе К и координатами х', у', z той же точки в системе К'. Если начать отсчет времени с того момента, когда начала координат обеих систем совпадали, то, как следует из рисунка - 1.6 x=x'+v0 t. Кроме того, очевидно, что у=у' и z=z'.
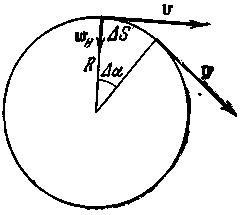 |  |
| Рисунок - 1.5 | Рисунок - 1.6 |
Добавив к этим соотношениям принятое в классической механике предположение, что время в обеих системах течет одинаковым образом, т. е. что t=t', получим совокупность четырех уравнений, называемых преобразованиями Галилея.
| x = x' + v0t', y = y', z = z', | (1.9) |
| t = t' | (1.10). |
В рамках ньютоновской механики эти формулы оказываются справедливыми с большой степенью точности. Продифференцировав соотношения (1.9) по времени, найдем связь между скоростями точки Р по отношению к системам отсчета К и К';
| x = x' + v0 у = у' z = z' | или или или | vx = v'x + v0, vy = v'y vz = v'z. | (1.11). |
Эти три скалярных соотношения эквивалентны следующему соотношению между вектором скорости v по отношению к системе К и вектором скорости v' по отношению к системе К':
| v = v' + v0 | (1.12). |
Полученные Галилеем преобразования дают правило сложения скоростей в классической механике. Следует иметь в виду, что данное соотношение остается справедливым при произвольном выборе взаимных направлений координатных осей систем К и К'. Таким образом, получается следующий результат: параметры, определяющие изменения состояния движения механических систем, инвариантны относительно преобразования Галилея. Это положение называется принципом относительности Галилея.
В общем случае произвольного криволинейного движения вектор скорости v может меняться и по величине и по направлению. Поэтому, будет целесообразно характеризовать каждый аспект в изменении скорости соответствующим ускорением:
- характеризующую быстроту изменения скорости по величине;
- характеризующую быстроту изменения ее по направлению.
Изменение направления вектора скорости за время dt характеризует вектор аn, который называется нормальным ускорением. Из чертежа (рисунок 1.7) видно, что оно направлено по радиусу кривизны (R) сторону вогнутости кривой и вычисляется по формуле:
| аn = v2/R | (1.13). |
Изменение величины скорости по времени характеризует ускорение аτ которое называется касательным, или тангенциальным ускорением, вычисляется по формуле:
| аτ = dv/dt | (1.14). |
Из рисунка следует, что вектора аn и аτ в каждый момент времени всегда перпендикулярны в каждой точке траектории, поэтому полное ускорение а в любой момент времени находится по теореме Пифагора:
| а = √ аn2+ аτ2 | (1.15). |
В зависимости от вида траектории можно различать прямолинейное движение и криволинейное движение.
