А. М. Мубараков

Вид материала

Содержание

1.1.5 Колебательное движение. Виды гармонических колебаний

Подобный материал:

1 2 3 4 5 6 7 8 9 ... 48

1.1.5 Колебательное движение. Виды гармонических колебаний

Колебаниями называются процессы, отличающиеся той или иной степенью повторяемости. Колебания широко распространены в природе и технике. Таким свойством повторяемости обладают, например, качания маятника часов, колебания струны или ножек камертона, напряжение между обкладками конденсатора в контуре радиоприемника и т. п.

В зависимости от физической природы повторяющегося процесса различают колебания: механические, электромагнитные, электромеханические и т. д. Несмотря на различие в физической природе колебаний, закономерности в процессе колебаний – одинаковы и, поэтому, их можно установить на примере любого из вышеназванных ее видов.

Простейшим случаем периодического колебания будет гармоническое колебание, при котором смещение х меняется со временем по закону косинуса или синуса:

х= A cos (ωt +φ₀), х= A sin (ωt +φ₀).

(1.30).

На рисунке - 1.16 приведен график зависимости х от t. На графике отмечена точка О' — другое начало отсчета времени t, при котором φ принимает нулевое значение, а уравнение колебания приобретает более простой вид х= Acosφ. Поскольку cos φ меняется в пределах от -1 до +1, то смещение х точки М от центра колебаний О находится в пределах: А<х<+А. Максимальная величина этого смещения |х|_m_акс= А называется амплитудой колебания. Аргумент φ = (ωt +φ₀), стоящий под знаком косинуса и синуса, определяющий, таким образом, долю (равную cos φ), которую смещение х составляет от максимального, называется фазой колебания или, коротко, фазой. Величина φ₀ есть соответственно начальная фаза колебания при t=0. Величина ω называется угловой частотой гармонического колебания точки М, которая связана с периодом Т и обычной циклической частотой υ (числом колебаний за единицу времени) следующим образом:

ω = 2π υ

(1.31).

Т = 2π/ω =1/υ

(1.32).

Дифференцируя уравнения колебания по времени, находим скорость колебательного движения точки М в любой момент времени:

v =dx/dt = - Aωsinωt.

(1.33).

Дифференцируя соотношение еще раз по t, найдем ускорение колеблющейся точки:

а =dv/dt = -Aω² cosωt.

(1.34).

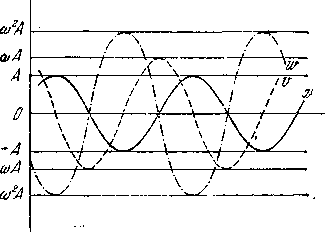
Мы видим, что скорость и ускорение колеблющейся точки меняются со временем также по гармоническому закону, с той же самой угловой частотой ω, но не в одной фазе: скорость опережает смещение по фазе на π/2, а и ускорение отстает по фазе от смещения на π/2 (рисунок - 1.17). Амплитуда колебаний скорости равна v₀ = Aω, а амплитуда колебаний ускорения а₀=-Aω².


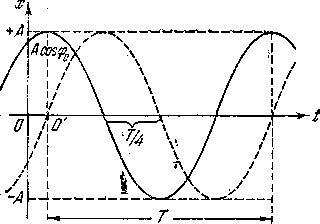Рисунок - 1.16	Рисунок - 1.17

Выясним, какими силами вызываются гармонические колебания, воспользовавшись законами динамики. По второму закону динамики сила F,

F = mа= - ma₀ cosωt = - mх,

(1.35).

Сравнивая эту силу, с силой упругостью из закона Гука (F =- kx), замечаем, что они обладают некоторой схожестью:

- величины сил прямо пропорциональны смещению точки от центра колебания;

- направление сил противоположны направлению смещения.

Силы, обладающие такими свойствами, называют «квазиупругими силами» (по-латыни «quasi» означает «как бы»). Таким образом, чтобы тело совершало гармоническое колебание, не обязательно, чтобы на нее действовали именно упругие силы. Достаточно, чтобы сила, определяющая смещение, обладала двумя вышеназванными особенностями, т.е. была квазиупругой силой.

В зависимости от характера воздействия сил на систему, различают свободные (или собственные) колебания, затухающие колебания и вынужденные колебания.

Свободными или собственными называются такие колебания, которые происходят под действием внутренних, собственных сил тела, после того, как оно было выведено из состояния равновесия. Примером могут служить колебания шарика, подвешенного на нити (маятник), сжатая или растянутая пружина и т.д.

Рассмотрим колебания тела, подвешенного на невесомой пружине. На тело массой m действуют упругая сила пружины F_упр= - kx, под действием которой тело совершает колебательное движение согласно второго закона Ньютона: F = ma, т.е., выполняется соотношение:

ma= - kx

(1.36).

Заменяя ускорение а второй производной от смещения по времени (а=d²x/d²t), получим дифференциальное уравнение собственных колебаний:

m d²x/d²t + kx = 0 .

(1.37).

Разделим обе части этого уравнения на m, произведя одновременную замену ω₀²= k/m:

d²x/d²t + ω₀²x = 0 .

(1.38).

Это и есть дифференциальное уравнение собственных колебаний любого маятника, решением которого и является уравнение гармонических колебаний

х= A cos ω₀t

(1.39).

Здесь ω₀- частота собственных колебаний тела массой m. Для пружинного маятника (тело, подвешенное на пружине)

ω₀= √k/m.

(1.40).

Зная ω₀, можно легко найти период колебания:

Т = 2π/ ω₀ = 2π√m/ k .

(1.41).

Тело, на которое действует упругая или квазиупругая сила, будучи выведена из положения равновесия х = 0, начнет совершать колебания около этого положения. Из-за наличия сил трения подобные реальные собственные колебания тела, всегда будут затухающими. Разберем аналогичным методом затухающие колебания при наличии сил трения. F_тр= -rv, где r - коэффициент сопротивления среды, где происходят колебания. Учет всех сил для затухающих колебаний дает следующее выражение закона динамики:

F_упр + F_тр = — kx—rv = ma.

(1.42).

После преобразований получим:

d²x/d²t + 2β dx/dt + ω₀²x = 0 .

(1.43).

- дифференциальное уравнение движения тела с массой т под действием квазиупругой силы и силы трения, где произведена замена :2β = r/m.

β = r/2m

(1.44).

Здесь β имеет смысл коэффициента затухания. Согласно теории дифференциальных уравнений в таком уравнении искомая функция x(t) должна обладать следующим свойством: как первая, так и вторая производная по времени от х (t) должны отличаться от самой функции х (t) лишь численными множителями. Такой функцией, в самом общем случае, является показательная функция с комплексным показателем степени или, что то же, произведение показательной функции на синус или косинус. Поэтому, решением полученного дифференциального уравнения затухающих колебаний будет

х = А₀е^-β^t соsωt

(1.45).

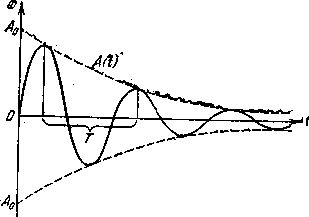
Оно отличается от идеального гармонического колебания тем, что амплитуда колебания А₀е^-β^t является убывающей функцией времени (рисунок - 1.18). Пунктиром на этом рисунке изображена зависимость амплитуды от времени, а сплошной линией — полная зависимость. Чем больше коэффициент трения β, тем быстрее амплитуда затухающих колебаний убывает со временем. Таким образом, затухающими будем называть такие колебания, амплитуда которых с течением времени уменьшается. При наличии трения убывает со временем не только амплитуда колебания, но и уменьшается угловая частота колебаний:

ω = √ω₀²- β²

(1.46),

где ω₀ — угловая частота собственных колебаний.

Сопоставим значения амплитуд двух соседних колебаний, отличающиеся друг от друга на один период, т. е., А(t) = A₀e^{- β}^t и А(t + Т) = A₀e^{- β {}^t⁺^T⁾, и разделив первое из этих значений на второе, получим:

А(t)/ А(t + Т) = e^-^β^t/ e^-^β^{t+T) = e^{- T} = const,

(1.47),

т. е. амплитуда затухающих колебаний за каждый период убывает в одно и то же число раз. Натуральный логарифм этого отношения

ln А(t)/ А(t + Т) = θ

(1.48)

носит название логарифмического декремента затухания. С коэффициентом затухания (β)он связан следующим образом:

θ = βТ

(1.49).

Для получения незатухающих колебаний необходимо воздействие дополнительной переменной внешней силы, которая непрерывно восполняла бы убыль энергии, затрачиваемой на преодоление трения. Подобная переменная сила называется вынуждающей силой (F_вын_),а возникающие под ее действием незатухающие колебания — вынужденными. Вынужденными называются такие колебания, в процессе которых колеблющаяся система подвергается воздействию внешней периодической силы

F_вын = F₀ cos ωt

(1.50).

Здесь F₀ есть амплитуда вынуждающей силы, т. е. максимальное возможное ее значение, ω — угловая частота колебаний вынуждающей силы. Полная сила, действующая на колеблющуюся точку, будет алгебраической суммой квазиупругой силы, силы трения и вынуждающей силы, и дифференциальное уравнение вынужденных колебаний примет вид m d²x/d²t = -kx-rv + F₀cos(ωt). Или

d²x/d²t + 2β dx/dt + ω₀²x = F₀/m cos(ωt)

(1.51).

Решение этого уравнения имеет вид

x = Acosωt

(1.52)

с неизвестными заранее амплитудой А и сдвигом фазы φ.

Под действием внешней вынуждающей силы возникают гармонические вынужденные колебания с частотой вынуждающей силы - ω. Амплитуда вынужденных колебаний прямо пропорциональна амплитуде вынуждающей силы F₀, зависит от характеристик свободно колеблющейся точки и является функцией угловой частоты колебаний вынуждающей силы ω:

А = F₀/√ (ω₀² – ω²)² + 4β²ω²

(1.53)

а фаза

φ = arctg 2βω/(ω₀² – ω²)

(1.54).

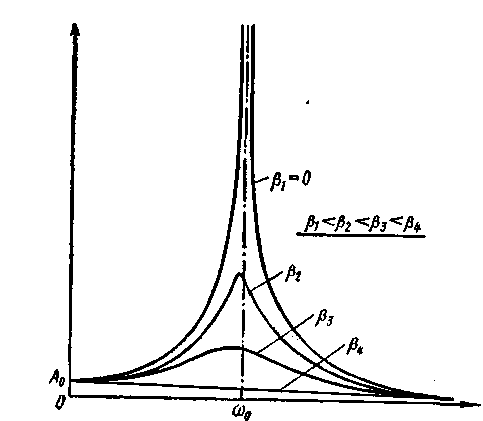
Графики зависимости А и сдвига фаз φ от ω (резонансные кривые) для нескольких значений β представлены на рисунке - 1.19. Как видно из графика, амплитуда колебаний сначала растет с увеличением циклической частоты ω вынуждающей силы F и при ω = ω₀ становится бесконечно большой. При дальнейшем росте циклической частоты ω амплитуда А вынужденных колебаний уменьшается, причем lim A = 0.


Рисунок - 1.18	Рисунок - 1.19

Явление резкого возрастания амплитуды вынужденных колебаний при приближении циклической частоты вынуждающей силы ω к собственной частоте ω₀ называется резонансом. Явление резонанса широко используется в радиотехнике (например, для настройки радиоприемников на прием той или иной радиостанции), в акустике (для анализа звуков, их усиления и т. д.). Ряд оптических явлений, например, аномальная дисперсия, связаны с резонансом.

Кинетическая энергия колеблющегося тела непрерывно меняется:

Е_кин = mv²/2 = (mA²ω₀²sin²ω₀t) /2 = mA²ω₀²(1- cos2ω₀t)

(1.55).

В силу того, что в Е_кин скорость входит во второй степени, знак ее не существен, т. е. Е_кин принимает последовательно при движении к (+А) те же значения, что и при движении от к (- А). Таким образом, Е_кин меняется со временем также по гармоническому закону, но по сравнению с координатой х — с удвоенной частотой. Физически удвоение частоты колебания Е_кин по сравнению с х объясняется просто. Кинетическая энергия дважды за период обращается в нуль в точках, где v = 0, — крайних точках движения и также два раза за период принимает максимальное значение в точках х = 0, где скорость v максимальна.

При вычислении потенциальной энергии квазиупругих сил условимся отсчитывать ее от положения равновесия, т. е. положим, что при х = 0, Е_пот = 0. Тогда, потенциальная энергия в точке х будет численно равна работе квазиупругой силы, совершенной при перемещении из положения равновесия в данную точку и взятой с обратным знаком: Е_пот = ∫F_упрdx . Учитывая, что F_упр = ma, найдем выражение для потенциальной энергии

Е_пот= m²ω₀²х²/2 = mA²ω₀²cos²ω₀t /2 = mA²ω₀²/4(1+ cos2ω₀t).

(1.56).

Следовательно, потенциальная энергия Е_пот меняется с частотой 2ω и в тех же пределах, что и Е_кин, но со сдвигом фазы относительно Е_кин на π. Полная энергия механического движения представляет собой сумму кинетической и потенциальной энергий.

Е = Е_кин + Е_пот = mA²ω₀²/2.

(1.57).

Таким образом, полная энергия гармонически колеблющейся точки есть величина постоянная и пропорциональная квадрату амплитуды колебаний А².В процессе движения происходит непрерывный переход кинетической энергии в потенциальную и обратно, но сумма их остается при этом постоянной. Когда точка проходит через положение равновесия х=0, потенциальная энергия обращается в нуль, а кинетическая максимальна и равна полной энергии. Когда же колеблющаяся точка доходит до одного из своих крайних положений х = i А, то v = 0, кинетическая энергия обращается в нуль, а потенциальная максимальна и равна полной энергии.

Среднее значение квадрата синуса и квадрата косинуса равно, как известно, половине. Следовательно, среднее значение ‹Е_кин› совпадает со средним значением ‹Е_пот› и равно Е/2.

Blog

Содержание

1.1.5 Колебательное движение. Виды гармонических колебаний