Методическое пособие по теме «тени на комплексном чертеже»

Вид материала

Методическое пособие

Содержание 2. Тень от точки и отрезка прямой 3. Тень от окружности 4. Тени от геометрических тел Тень от параллелепипеда. Тень от цилиндра. 1 – 2 циркулем переносится на сторону квадрата, полученная точка 3 Тень от сферы. 5. Способы построения теней 5.1. Способ лучевых сечений 5.2. Способ касательных конусов 5.3. Способ «выноса» 5.4. Способ биссекторных горизонталей O и оси поверхности. Далее через тень от центра O 5.5. Способ обратных лучей 5.6. Способ вспомогательных экранов 6. Тени архитектурных форм 6.1. Тень от круглой плиты на колонну 6.2. Тень от квадратной плиты на колонну 6.3. Тень от круглой и квадратной плиты на колонны с каннелюрами 6.4. Тень от валика на колонну ... Полное содержание

Подобный материал:

• Задание геометрического образа на комплексном чертеже посредством определителя. Задание, 32.56kb.
• 3 Виды поверхностеЙ и их проекции, 84.24kb.
• 12. ломаные и кривые линии (плоские и пространственные). Винтовая линия, 91.72kb.
• Методическое пособие в помощь для обучения нотариусов по теме: «Собственность недвижимое, 1868kb.
• Методическое пособие по внеаудиторной самостоятельной работе студентов Специальности, 144.38kb.
• Учебно-методическое пособие содержит тематический указатель по данному курсу, перечень, 627.01kb.
• Методическое пособие по французскому языку по теме «Страноведение», 793.91kb.
• Учебно методическое пособие Архангельск 2012, 824.52kb.
• В. А. Жернов апитерапия учебно-методическое пособие, 443.6kb.
• Методическое пособие Для учителя немецкого языка в рамках учебной программы по теме:, 303.48kb.

М.А. Айгунян

Методическое пособие

по теме

«ТЕНИ НА КОМПЛЕКСНОМ ЧЕРТЕЖЕ»


Для студентов направления

«Архитектура»


Москва

Российский университет дружбы народов

2008

1. ВВЕДЕНИЕ


Построение теней на комплексном чертеже придает большую реалистичность изображению за счет придания рельефности. Для этого необходимо знание физических и геометрических закономерностей построения теней. Знание физических закономерностей позволяет построить так называемую «воздушную перспективу», близкую к нашему зрительному восприятию и зависящую от степени освещенности, состояния воздушной среды, глубины расположения элементов, отраженного освещения, рефлексов, бликов. В настоящем курсе рассматриваются только геометрические закономерности построения теней, т.е. методы построения контуров теней.

Тени образуются от предметов при наличии источников освещения, которые могут быть точечными или бесконечно удаленными (например, солнце). В первом случае световые лучи исходят из одной точки, а во втором - параллельны между собой. Обычно световые лучи освещают часть предмета. Часть предмета, на которую не падают световые лучи, находится в собственной тени. Линия, ограничивающая эту тень, называется контуром собственной тени. Контур собственной тени образуют лучи, касающиеся предмета. Совокупность точек касания световых лучей образует контур собственной тени. Поверхность, образуемая касательными световыми лучами, называется лучевой поверхностью. Тень, падающая от одного предмета на другой, называется падающей тенью. Линия, ограничивающая эту тень, называется контуром падающей тени.

Построение падающих теней можно сравнить с построением очерка предметов при параллельном косоугольном проецировании (световые лучи параллельны) и центральном проецировании (световые лучи исходят из точечного источника света).

На архитектурных чертежах тени строят в основном на фасадах, в перспективных проекциях, в аксонометрии. Гораздо реже тени строятся на планах и разрезах. Построение теней на фасадах равносильно построению теней на фронтальной проекции комплексного чертежа. Горизонтальные проекции теней строятся в тех случаях, когда без них невозможно построить фронтальную проекцию тени.

Направление световых лучей, исходящих от солнца зависит от времени суток, времени года и географического местоположения. При построении теней на комплексном чертеже эти факторы не учитываются, а световые лучи считаются параллельными и направленными вдоль диагонали куба, грани которого параллельны плоскостям проекций (рис.1.1). 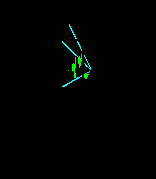В этом случае проекции световых лучей на плоскости проекций s₂ и s₁ составят угол 45⁰ к линиям связи. Угол наклона светового луча s к граням куба составляет ~ 35⁰. Такое направление светового луча значительно облегчает построения.

Подводя итог, можно сказать, что с геометрической точки зрения, построение теней представляет решение двух задач:

а) построение линии касания световых лучей (лучевой поверхности) и заданного геометрического образа, т.е. выявление контура собственной тени;

б) построение линии пересечения лучевой поверхности с поверхностью, на которую падает тень, т.е. решение второй главной позиционной задачи о пересечении двух поверхностей. При этом лучевая поверхность является в общем случае цилиндрической с направляющей, роль которой играет контур собственной тени. Контур падающей тени, таким образом, является тенью от контура собственной тени.


^ 2. ТЕНЬ ОТ ТОЧКИ И ОТРЕЗКА ПРЯМОЙ


Для получения тени от точки необходимо провести через эту точку световой луч до пересечения его с поверхностью, на которую строится тень. Таким образом, задача о нахождении тени от точки сводится к решению первой главной позиционной задачи, т.е. задаче о пересечении прямой и поверхности. На рис.2.1 и 2.2 показано построение тени от точки A на горизонтальную и фронтальную плоскости уровня, т.е. решается первая главная позиционная задача во втором случае, когда один из образов занимает проецирующее положение. На рис.2.3 показано построение тени от точки M на плоскость общего положения, заданную треугольником ABC (первая главная позиционная задача в третьем случае, когда ни один из геометрических образов не занимает проецирующего положения).



Тень от отрезка прямой линии на плоскость может быть построена по двум точкам (рис.2.4). В случае если тень от отрезка прямой попадает на две плоскости, т.е. тень получается «ломаной», необходимо построить вспомогательную точку C (рис.2.5) или использовать фиктивную тень точки B (рис.2.6). Второй способ предпочтительнее, т.к. требует меньше построений.



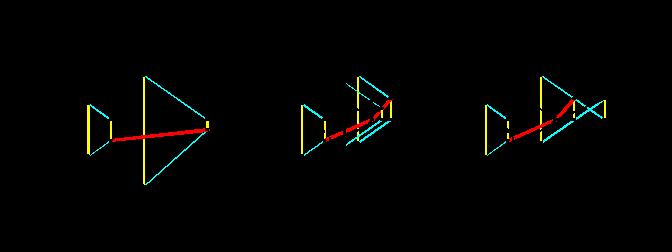
Тени от прямых частного положения обладают рядом особенностей:

1. Тени от отрезков фронталей и горизонталей располагаются параллельно проекциям отрезков на плоскостях, которым они параллельны (рис.2.7).
   
2. Тени от отрезков проецирующих прямых располагаются по направлению проекции светового луча (т.е. под углом 45⁰) на плоскость, по отношению к которой отрезок перпендикулярен. В случае если тень «ломаная», на другой плоскости тень параллельна соответствующей проекции отрезка, т.е. вертикальна (рис.2.8).
   
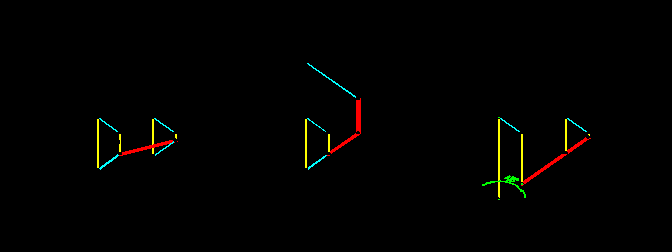
3. Тень от горизонтали, расположенной под углом 45⁰ к фронтальной плоскости (так называемая «биссекторная» горизонталь), располагается либо как тень проецирующей прямой (рис.2.9 и 2.10), либо (угол 45⁰ в другую сторону) на фронтальной плоскости отрезок тени расположен с уклоном 1:2 (рис.2.11).
   
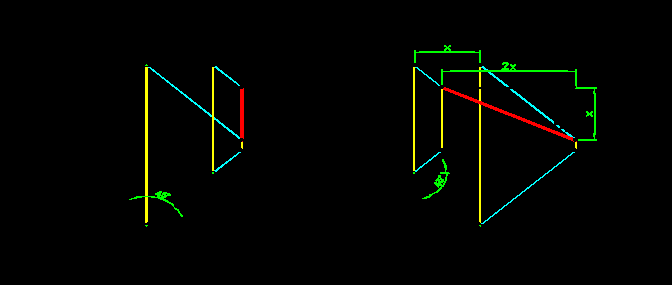
4. Тень от плоской фигуры на плоскость, ей параллельную, является точно такой фигурой и для ее построения достаточно построить тень от одной точки.
   

^ 3. ТЕНЬ ОТ ОКРУЖНОСТИ


Тень от окружности на плоскость, ей параллельную, является окружностью и для ее построения достаточно построить тень от центра окружности O (рис.3.1 и 3.2). На рис.3.1 изображена окружность, расположенная в горизонтальной плоскости, и тень ее полностью попадает на горизонтальную плоскость. На рис.3.2 окружность изображена во фронтальной плоскости и тень от нее полностью падает на фронтальную плоскость. Построение тени от окружности в общем случае осуществляется через описанный вокруг нее квадрат (рис.3.3).

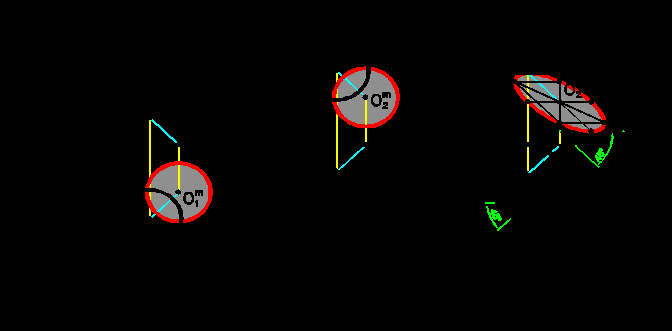
Тень описанного квадрата является параллелограммом со сторонами под углом 45⁰, одна диагональ которого вертикальна. Тень от окружности строится по восьми точкам. Из них четыре точки – это точки касания квадрата и окружности и четыре точки – это точки пересечения окружности и диагоналей квадрата. Точки пересечения диагоналей с окружностью можно найти, если половину стороны квадрата поделить в отношении 0.707 и через полученные точки провести прямые, параллельные соседним сторонам квадрата. Описанные построения можно осуществить непосредственно на фронтальной плоскости проекций, не прибегая к использованию горизонтальной. На рис.3.4, 3.5, 3.6 представлено построение теней при различных положениях окружности в пространстве.




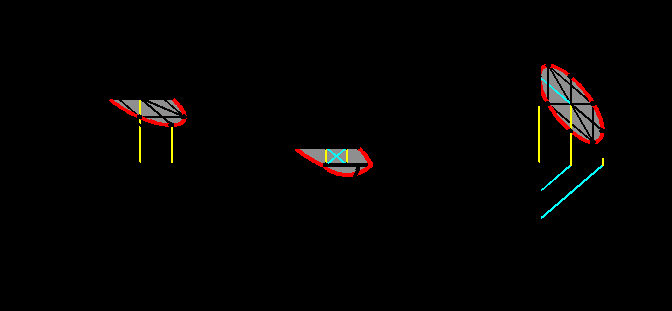
^ 4. ТЕНИ ОТ ГЕОМЕТРИЧЕСКИХ ТЕЛ


Как уже говорилось выше, падающая тень от геометрического образа является тенью от линии, являющейся контуром его собственной тени. Поэтому в общем случае вначале определяется контур собственной тени геометрического образа, а затем контур падающей. Далее рассматривается построение теней от простейших геометрических тел: параллелепипеда, цилиндра, конуса, шара (сферы).

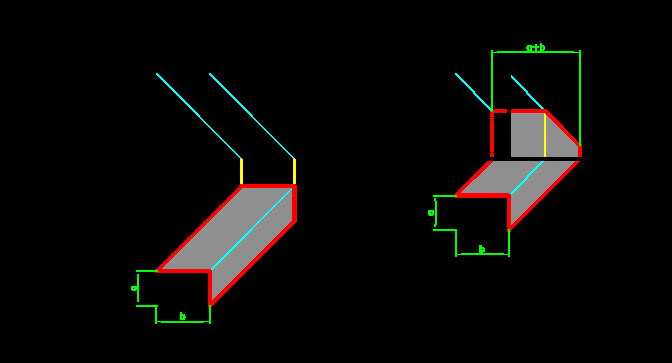
^ Тень от параллелепипеда. Контур собственной тени параллелепипеда ограничен прямыми линиями и поэтому построение теней от него не нуждается в комментариях (рис.4.1, 4.2). Необходимо лишь отметить, что если грани его параллельны плоскостям проекций, то ширина тени составляет величину a+b, т.е. сумму длин сторон основания.



^ Тень от цилиндра. Контур собственной тени вертикального цилиндра образован полуокружностью верхнего основания, полуокружностью нижнего основания и двумя образующими, которых касаются световые лучи (рис.4.3). Поэтому для построения падающей тени необходимо построить в общем случае тени от верхней и нижней окружностей и двух образующих. На рис.4.4, 4.5, 4.6 показано построение теней для различных положений цилиндра в пространстве, а также половины цилиндра, примыкающего к фронтальной плоскости.






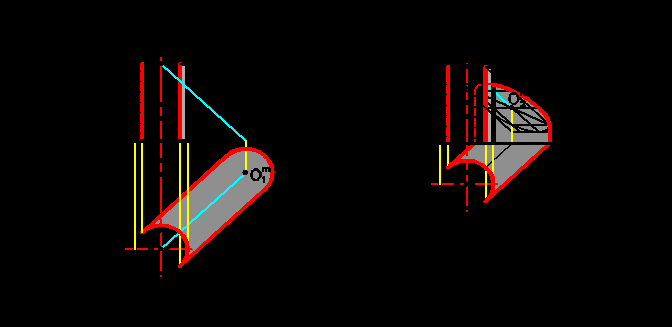
Тень от конуса. В отличие от других геометрических тел для конуса вначале строится падающая тень и лишь потом собственная. Для этого строится падающая тень от вершины конуса (рис.4.7). Из полученной точки S₁^т проводятся касательные прямые к основанию конуса. Контур, образованный этими касательными, и часть контура основания являются контуром падающей тени конуса. Образующие конуса, проведенные из точек касания, являются контуром собственной тени конуса. Если тень от вершины конуса падает на фронтальную плоскость, то строится, так называемая, фиктивная тень от вершины на горизонтальную плоскость, проводятся касательные к основанию конуса из этой точки, но только в пределах горизонтальной плоскости. Точки на линии пересечения плоскостей соединяются с истинной тенью от вершины (рис.4.8).



В случае если конус обратный, для построения собственной тени строится фиктивная тень от вершины на плоскость, в которой находится основание конуса (рис.4.9) и из нее проводятся касательные к основанию конуса.

На рис.4.10 представлена половина конуса, примыкающего к фронтальной плоскости и отстоящего от горизонтальной плоскости. Контур падающей тени такого конуса образован контуром падающей тени окружности основания и прямой, исходящей из вершины, (т.к. вершина конуса лежит во фронтальной плоскости) и касательной к тени от окружности. Если из точки касания провести обратный луч до основания, то из полученной точки 1 можно провести образующую, являющуюся контуром собственной тени.



На рис.4.11 и 4.12 представлены два конуса, у которых углы при основании равны 45⁰ и 35⁰ соответственно. Контур собственной тени для конуса с углом 45⁰ при основании образуют профильная и контурная образующие. Контур собственной тени для конуса с углом 35⁰ при основании вырождается в прямую, являющуюся образующей, совпадающей со световым лучом. Конусы с углами, меньшими 35⁰, не имеют собственной тени. Боковая поверхность таких конусов полностью освещена и не дает падающей тени.




На рис.4.13 показано графическое построение угла 35⁰ .Для этого строится квадрат, размер диагонали ^ 1 – 2 циркулем переносится на сторону квадрата, полученная точка 3 соединяется с точкой 4. Угол между отрезками 1 – 3 и 3 – 4 составляет 35⁰.

Конусы с углами при основании 45⁰ и 35⁰ в дальнейшем будут использоваться при построении теней более сложных форм, т.к. положение их собственных теней заведомо известно и легко строится.

^ Тень от сферы. Собственная тень сферы является эллипсом, большая ось которого равна диаметру сферы d, а малая ось приблизительно равна 0,6d (рис.4.14).

Дополнительные точки на контуре собственной тени можно построить проведением вертикальных и горизонтальных прямых из концов большой оси до пересечения с вертикальной и горизонтальной осями сферы. Смысл построений станет ясен при изучении способов построения теней. Падающая тень от сферы является эллипсом, для построения которого строится тень от центра сферы. Перпендикулярно направлению проекции светового луча расположена малая ось этого эллипса, равная по величине диаметру сферы. Величина большой оси определяется засечкой, равной диаметру сферы, из концов малой оси на направление большой и равна 1,7d. На рис.4.15 построена тень от полусферы на фронтальную плоскость проекций.




^ 5. СПОСОБЫ ПОСТРОЕНИЯ ТЕНЕЙ


При построении теней используются различные способы построения. Выбор способа зависит от характера конкретной задачи, но основной критерий при выборе способа заключается в максимальной точности решения и минимуме графических построений.


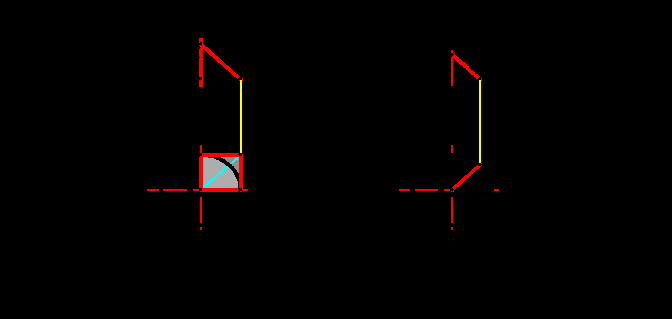
^ 5.1. Способ лучевых сечений


Способ лучевых сечений является основным и позволяет построить как собственные, так и падающие тени. С его помощью можно решить любую задачу на построение теней, однако, несмотря на его универсальность, в ряде случаев прибегают к использованию других менее трудоемких способов. На рис.5.1 представлено построение теней от одной поверхности общего вида на другую. Суть способа заключается в следующем. Световой луч заключается в лучевую плоскость (в данном случае горизонтально проецирующую плоскость Σ). Находится линия пересечения a лучевой плоскости Σ с поверхностью Φ, которая отбрасывает тень, и линия пересечения b с поверхностью Ω, на которую падает тень. Далее на фронтальной плоскости проекций проводятся касательные световые лучи к первой линии пересечения a до их пересечения со второй линией пересечения b. В данной задаче два касательных световых луча, которые в двух точках 1 и 2 пересекают линию b. Полученные точки 1 и 2 лежат на контуре падающей тени от поверхности Φ на поверхность Ω. Точки касания световых лучей 1^/ и 2^/ к поверхности Φ лежат на контуре ее собственной тени.

Проведя несколько лучевых плоскостей (сечений) можно получить ряд точек на контуре собственной и падающей теней. Совокупность точек пересечения световых лучей, касательных к линиям пересечения с первой поверхностью Φ, с линиями пересечения со второй поверхностью Ω даст контур падающей тени на эту поверхность. Совокупность их точек касания даст контур собственной тени поверхности Φ.





^ 5.2. Способ касательных конусов


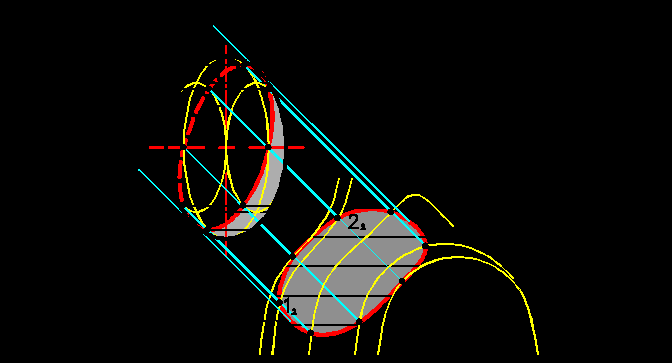
Способ касательных конусов предназначен для построения только собственных теней поверхностей вращения с осью, перпендикулярной плоскости проекций. Суть способа заключается в следующем. Если к поверхности вращения построить касательный к ней конус вращения (или цилиндр вращения), то точки, лежащие одновременно на контуре собственной тени конуса (или цилиндра) и на линии и на линии касания, которая является окружностью, будут также лежать и на контуре собственной тени исходной поверхности вращения. В качестве таких конусов используются конусы с углом наклона образующей 45^о и 35^о, для которых известно положение образующих, являющихся контурами собственной тени (рис.5.2).

Касательный цилиндр касается поверхности вращения по экватору. Точки 1 и 2 получены как на цилиндре с радиусом основания, равным радиусу экватора. Точки 3 и 4 получены как на конусе с углом при основании 45^о. Точки 5 и 6 получены как на таком же обратном конусе. Высшая точка 7 и низшая точка 8 получены как на конусе с углом при основании 35^о прямом и обратном соответственно.

Способ позволяет без использования горизонтальной проекции построить по восьми характерным опорным точкам собственную тень поверхности вращения.


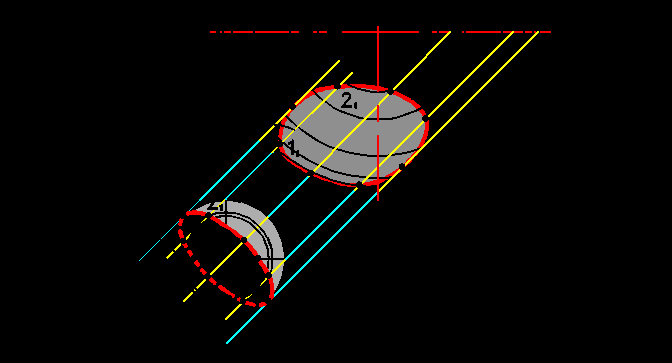
^ 5.3. Способ «выноса»


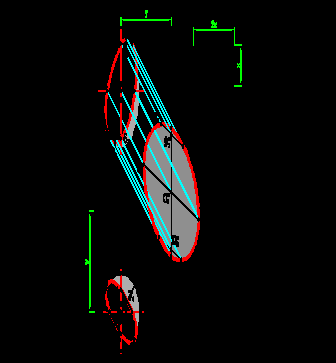
Способ предназначен для построения падающих теней в случае, если известны расстояния («вынос») характерных точек контура собственной тени до плоскости, на которую падает тень. На рис.5.3а представлен принцип способа. Если расстояние от точки A до фронтальной плоскости, на которую строится тень, известно и равно, например a, то достаточно на фронтальной плоскости отложить от точки A₂, по горизонтали отрезок величиной a, провести через полученную точку вертикальную прямую, а через точку A₂ луч под углом 45^о. В пересечении эти прямые дадут точку A₂^т, являющуюся тенью от точки A на фронтальную плоскость.

Способ особенно удобен для поверхностей вращения, если известен контур собственной тени и «вынос» оси вращения (рис.5.3б). На чертеже горизонтальная проекция дана для пояснения. Каждая из восьми характерных точек контура собственной тени имеет «вынос», легко вычисляемый и зависящий от «выноса» оси. Точки 3 и 5 имеют такой же «вынос» как и ось, равный y. Точки 4 и 6 имеют «вынос» (y-a) и (y+a) соответственно, где a является радиусом параллели, на которой они находятся. Тень от самой оси является вертикальной прямой, проходящей через точку O, «вынос» которой равен y. «Вынос» точек 1 и 2 равен (y-c) и (y+c) соответственно. «Вынос» точек 7 и 8 равен (y-b) и (y+b) соответственно. Соединив полученные тени от точек 1 – 8, можно получить тень от заданной поверхности на фронтальную плоскость без использования плана, зная лишь расстояние от оси до этой плоскости. При построении тени необходимо учесть, что ее контур не должен выходить за пределы лучей, проходящих через точки 3^т и 5^т, а также вертикальных прямых, проходящих через точки 1^т и 2^т.


^ 5.4. Способ биссекторных горизонталей


Способ предназначен для построения падающих теней в случаях, если характерные точки контура собственной тени могут быть попарно соединены прямыми, являющимися биссекторными горизонталями. Способ основан на свойстве тени от биссекторной горизонтали на фронтальной плоскости располагаться с уклоном 1:2 (рис.2.11). Применяется этот способ в тех же случаях, что и способ «выноса». Иногда оба способа могут применяться в комплексе. На рис.5.4 вначале по «выносу» построена тень от точки ^ O и оси поверхности. Далее через тень от центра O₂^т проводится прямая с уклоном 1:2. Полученная прямая является тенью от биссекторной горизонтали, соединяющей точки 1 и 2. Лучи, проведенные под углом 45^о, из точек 1₂ и 2₂ до пересечения с тенью от биссекторной прямой, проходящей через точку O₂^т, дадут тени от точек 1 и 2. Прямые, соединяющие точки 3 и 4, а также точки 5 и 6, также являются биссекторными горизонталями. Таких горизонталей можно провести сколько угодно. Для поверхностей второго порядка кривая контура собственной тени является плоской кривой, а прямая, соединяющая высшую и низшую точки 7 и 8, является геометрическим местом серединных точек биссекторных горизонталей. Тень прямой 7 – 8 совпадает с тенью от оси вращения (см. предыдущий пример). Далее строятся тени от серединных точек 9 и 10 горизонталей 3 – 4 и 5 – 6. Через полученные точки 9₂^т и 10₂^т, проводятся прямые, параллельные 1₂^т и 2₂^т, которые в пересечении с лучами из точек 3, 4, 5 и 6 дадут точки на контуре падающей тени. Горизонтальная проекция дана для пояснения и не используется в построениях.


^ 5.5. Способ обратных лучей


Способ предназначен для построения падающих теней от одного объекта на другой, если хотя бы один из них может включать в себя прямые линии или окружности. Суть способа заключается в следующем. От обоих объектов строятся падающие тени на какую-либо плоскость (уровня или проецирующую). Из точки пересечения теней на эту плоскость проводится «обратный луч» (иногда прямой) до пересечения с линией, давшей тень. Полученная точка является одной из точек контура искомой тени. На рис.5.5а представлено построение тени от отрезка прямой AB на поверхность конуса вращения.

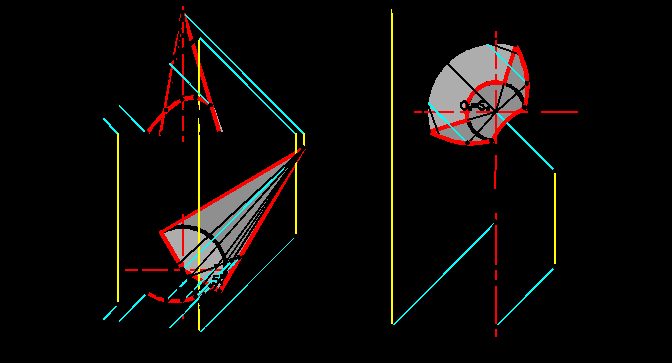Строится тень от отрезка AB и конуса на горизонтальную плоскость проекций. На поверхности конуса строится ряд образующих и тени от этих образующих. Из точек пересечения теней от образующих с тенью от отрезка A₂^т B₂^т проводятся обратные лучи до пересечения с соответствующими образующими, давшими тень. Полученные точки 1^к, 2^к, 3^к, 4^к, 5^к являются тенями от точек отрезка AB на поверхность конуса. Точка 1^к могла быть определена и без построений, как лежащая одновременно на горизонтальной плоскости проекций и поверхности конуса. Точка 5^к, так называемая точка «исчезновения» тени, должна быть обязательно построена. Она лежит на контуре собственной тени конуса и без нее невозможно правильно выявить характер линии 1^к – 5^к.

Этим же способом построена тень внутри конической ниши (рис.5.5б). Выявляется контур собственной тени конуса путем построения фиктивной тени S^ф от достроенной вершины S. Участок окружности основания конуса между точками A и B будет отбрасывать тень на внутреннюю боковую поверхность конуса и на плоскость второго основания конуса. Тень на второе основание строится как тень от окружности на плоскость, ей параллельную. Т.е. достаточно построить тень от центра окружности O на плоскость второго основания O^т и из ее фронтальной проекции O₂^т провести дугу окружности радиусом, равным радиусу первого основания. Дуга между точками C и D является частью контура падающей тени. На участке между точками A и C, а также B и D строятся образующие 1S и 2S и фиктивные тени от них на плоскость первого основания 1S^ф и 2S^ф. Из точек их пересечения с дугой окружности AB 3 и 4 проводятся прямые лучи до пересечения с соответствующими образующими. Полученные точки 5 и 6 являются точками, принадлежащими контуру падающей тени на внутреннюю поверхность конуса.


^ 5.6. Способ вспомогательных экранов


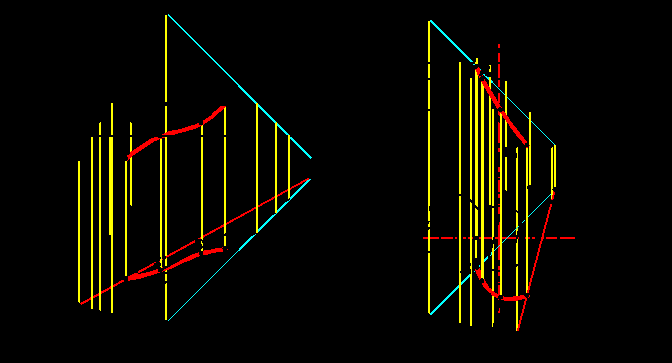
Способ предназначен для построения падающих теней на поверхности, которые могут быть пересечены плоскостью (экранами) по прямой или по окружности, т.е. в тех же случаях, что и способ обратных лучей. Иногда способы используются в комплексе. Суть способа заключается в следующем. Поверхность пересекается плоскостью (экраном), параллельной плоскости проекций. На эту плоскость строится тень от линии, дающей тень. Точки пересечения полученной тени от линии с линией пересечения поверхности экраном являются точками, лежащими на контуре падающей тени от исходной линии на исходную поверхность. Т.к. экраны параллельны друг другу, то тени на них от исходной линии также параллельны и их повторное построение не составляет труда. Совокупность точек, полученных от нескольких экранов, позволят построить контур падающей тени от исходной линии на заданную поверхность. На рис.5.6а представлено построение падающей тени от отрезка прямой AB на цилиндрическую поверхность Φ. При пересечении цилиндрической поверхности плоскостями уровня Γ, Γ^/, Γ^//, Γ^/// получаются прямые a,a^/, a^//,a^///. В роли первого экрана Γ выступает сама плоскость проекций. На плоскости Γ тень от прямой A₁^т B₁^т пересекается с линией пересечения a в точке 1₁^ф. На следующих экранах тень от прямой строится параллельно тени на первый экран и через точку пересечения прямой с экраном. Точки 2^ф, 3^ф, 4^ф найдены в пересечении тени от прямой на экраны с прямыми a^/, a^//,a^///.

На рис.5.6б представлено построение тени от отрезка прямой AB на поверхность вращения Φ. Экраны Γ^/, Γ^//, Γ^/// пересекают поверхность вращения по окружностям. Остальные построения аналогичны предыдущему примеру. Продолжение линии тени построено для выявления положения точки A^ф.




^ 6. ТЕНИ АРХИТЕКТУРНЫХ ФОРМ


В настоящей главе рассматривается построение теней наиболее часто используемых на практике архитектурных форм. В общем случае тени на фасаде всегда можно построить, используя способ лучевых сечений при наличии плана. Однако встречается множество частных случаев, в каждом из которых возможно использование особенностей данной архитектурной формы, что значительно сокращает трудоемкость построений и тем самым облегчает выполнение и понимание чертежа.


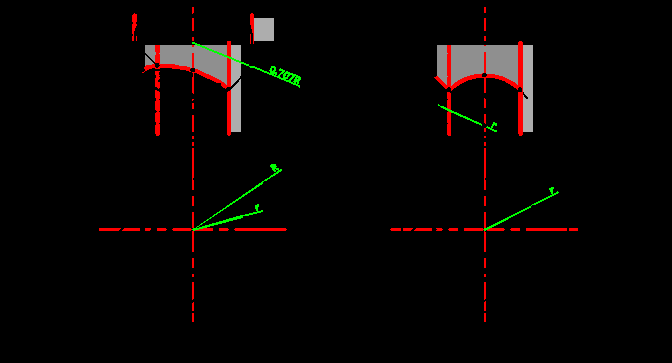
^ 6.1. Тень от круглой плиты на колонну


Тень от круглой плиты на колонну строится без построения тени на стену и без использования плана, который на чертеже показан только для пояснения построений, выполняемых на фасаде (рис.6.1). Тень на колонну падает от части окружности нижнего основания плиты от точки 4^/ до точки 4. Тень 1₂^т на левую контурную образующую получена наложением плана на фронтальную проекцию. Т.е. проведена дуга радиусом, равным радиусу плиты, из конечной точки левой контурной образующей проведен луч под 45^о до пересечения с дугой, из полученной точки пересечения 1₂^ф проведена горизонтальная прямая до пересечения с контурной образующей. Полученная точка 1₂^т является тенью на левую контурную образующую. Исходя из условия полной симметрии относительно лучевой плоскости, проходящей через ось цилиндра, тень 3₂^т на профильную образующую цилиндра будет находиться на той же горизонтали, что и тень на левой контурной образующей. Тень от точки 2, находящейся на бликовой образующей верхней плиты на расстоянии 0,707 от оси, попадает также на бликовую образующую нижнего цилиндра. Поэтому из точки 2 проводится луч под 45^о до пересечения с бликовой образующей нижнего цилиндра. Полученная точка 2₂^т будет высшей. Точка исчезновения тени 4₂^т получена в пересечении контура собственной тени колонны и окружности радиусом, равным 0,707 от радиуса верхней плиты. Точка 4₂^т может быть получена подобным построением, потому что если использовать способ вспомогательных биссекторных экранов, то тень на такой экран от окружности плиты проецируется в виде эллипса, который, в свою очередь, на фронтальной плоскости проекций представится окружностью радиуса 0,707R. Образующая, являющаяся контуром собственной тени, находится в биссекторной плоскости Δ. Поэтому точка пересечения этой образующей и такой окружности является тенью на эту образующую.





^ 6.2. Тень от квадратной плиты на колонну


Тень от квадратной плиты на колонну (рис.6.2) также строится без построения тени на стену и без использования плана. Тень на колонну падает от двух прямых нижнего основания плиты от точки 4^/ до точки 4. Одна из этих прямых фронтально проецирующая, а вторая – профильно проецирующая. Тени от обеих прямых на колонну (цилиндр) являются дугами эллипсов. От фронтально проецирующей прямой эта дуга эллипса проецируется в виде прямой, а от профильно проецирующей прямой – в виде дуги окружности радиусом, равным радиусу цилиндра. Центр этой окружности расположен на пересечении оси и светового луча из точки 1. Точка 1₂ и точка исчезновения тени 4₂^т находятся на одной параллели. Также на одной параллели находятся точки 2₂^т и 3₂^т. Оба утверждения справедливы для квадратной плиты.


^ 6.3. Тень от круглой и квадратной плиты на колонны с каннелюрами


Тень от круглой плиты на колонну с каннелюрами (рис.6.3) строится как на обычную гладкую колонну, но дважды. В роли первой колонны выступает цилиндрическая поверхность, проходящая через ребра каннелюр, в роли второй колонны – цилиндрическая поверхность, касающаяся каннелюр. Собственные и падающие тени на обе цилиндрические поверхности строятся как в п.6.1. Истинная падающая тень является волнистой линией, которая проходит через точки пересечения ребер каннелюр с контуром первой падающей тени и касается контура второй падающей тени. Необходимо также построить собственные и падающие тени внутри каннелюр как в цилиндрических нишах (см. далее).

Аналогичным образом строятся тени от квадратной плиты на колонну с каннелюрами (рис.6.4).




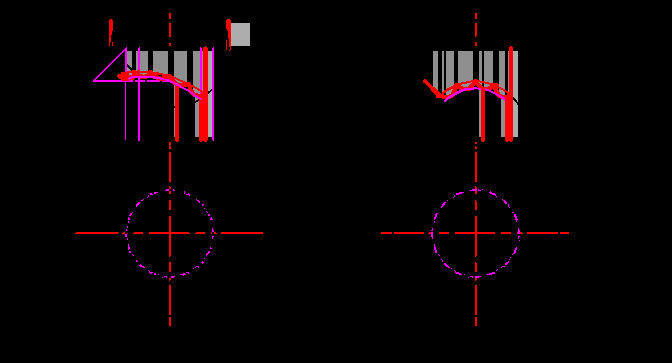
^ 6.4. Тень от валика на колонну


Тень от валика на колонну (рис.6.5) строится с помощью падающей тени от валика на стену. Строится контур собственной тени валика 1₂ - 2₂ - 3₂ - 4₂ - 5₂ - 1₂ и цилиндра. Способом «выноса» строится падающая тень от валика и цилиндра на стену, проходящую через ось валика и цилиндра. Точки, лежащие на контурных образующих цилиндра, принадлежат одновременно стене и цилиндру. Поэтому точка 6₂^в, лежащая на контуре падающей тени от валика на стену, принадлежит также контуру падающей тени от валика на цилиндр. Исходя из условия полной симметрии, точка 7₂^в, лежащая на профильной образующей, принадлежит той же параллели цилиндра, что и точка 6₂^в. Точка 2₂, лежащая на бликовой образующей, является тенью от точки 2₂ и может быть получена следующим образом.

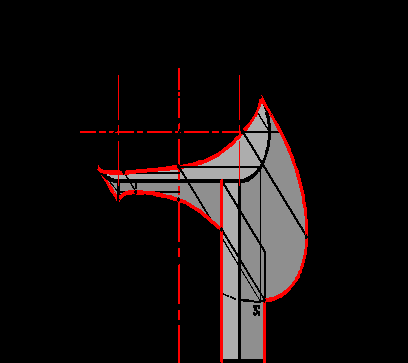
Если из контурной точки параллели валика, на которой лежит точка 2₂, провести луч под углом 35^о до пересечения с контуром цилиндра и через полученную на контуре точку провести параллель цилиндра, а из точки 2₂ провести луч под углом 45^о, то последний пересечет параллель в точке 2₂^в. Точка 2₂^в будет высшей на контуре падающей тени от валика на цилиндр. Точка исчезновения тени 8₂^в, лежащая одновременно на контуре собственной тени цилиндра и падающей тени от валика на цилиндр, строится с помощью обратного луча из точки пересечения падающих теней валика и цилиндра на стену.


^ 6.5. Тень от скоции


Способом касательных конусов строится собственная тень скоции (рис.6.6).

Затем способом «выноса» строится падающая тень на фронтальную стену от верхней окружности. После этого строится падающая тень от окружности на поверхность скоции по тем же принципам, что и тень от валика на цилиндр. В зависимости от пропорций скоции падающая тень может частично или полностью перекрывать ее собственную тень



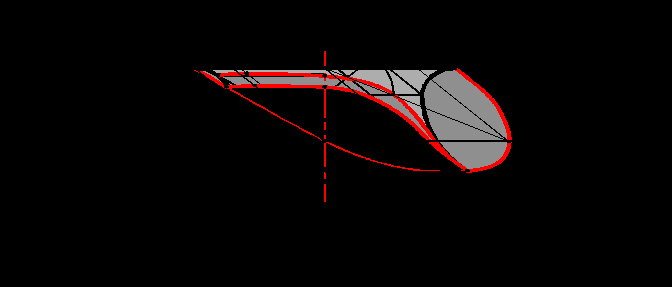
^ 6.6. Тень от квадратной плиты на поверхность вращения (способ цилиндрических экранов)


Тень от квадратной плиты на поверхность вращения произвольного вида (рис.6.7) строится как тень от квадратной плиты на цилиндр. 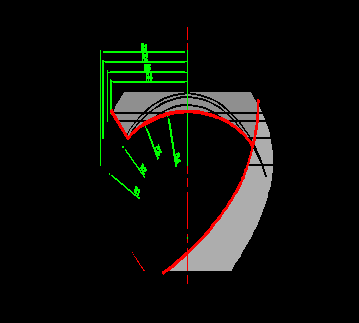При этом используется несколько соосных с поверхностью вращения и пересекающих ее цилиндров. На каждом из этих цилиндров строится тень от квадратной плиты, состоящая из двух участков: первый – прямая, совпадающая с направлением светового луча, второй – дуга окружности радиусом, равным радиусу данного цилиндра. Из всей дуги на контуре падающей тени находятся лишь те точки, которые являются общими для поверхности вращения цилиндра, т.е. точки пересечения дуги окружности и параллели, соответствующей данному цилиндру. Центр всех дуг находится в точке пересечения световых лучей из угловой точки плиты с осью поверхности вращения. Накопив достаточное количество точек, можно с любой степенью точности построить криволинейный участок контура падающей тени на поверхность вращения. Прямолинейный участок будет иметь место также как и в случае с цилиндром. Точность построения тени от угловой точки зависит от точности построения криволинейного участка тени. Подобный способ построения носит название способ цилиндрических экранов.


^ 6.7. Тени в нишах


Ниши являются архитектурной формой, часто используемой на практике и представляющие собой внутренние поверхности призм, цилиндров, конусов и сфер.

На рис.6.8 представлена призматическая ниша. Падающие тени от контура ниши (он же контур собственной тени) на внутреннюю поверхность задней грани призмы, являющейся фронтальной плоскостью, строятся по «выносу», который равен глубине ниши.

На рис.6.9 представлена цилиндрическая ниша с открытым верхом. Строится собственная тень цилиндра известным способом. Затем строятся падающие тени от контура собственной тени ниши, состоящего из левой вертикальной прямой и дуги окружности от точки 1 до точки 2. Падающая тень от вертикальной прямой на цилиндрическую поверхность падает на образующую, совпадающую с осью.




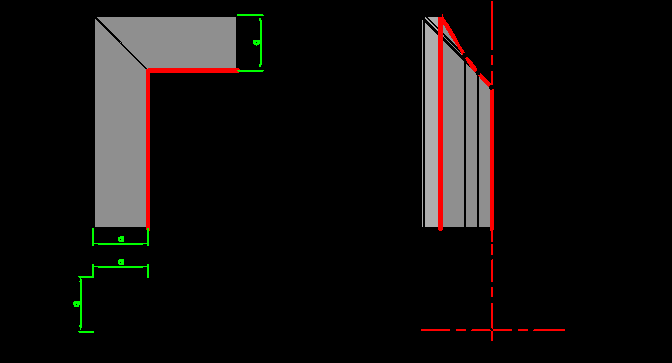
Последняя точка ^ 1 дает тень в точке 1₂^т. Далее строится тень от дуги окружности 1 – 2. Тень от точки 2 совпадает с самой точкой 2. Тени от промежуточных точек 3 и 4 позволяют построить падающую тень 1₂^т - 2₂^т, являющуюся дугой эллипса.

На рис.6.10 представлена цилиндрическая ниша с закрытым верхом. После построения собственной тени строятся падающие тени от контура собственной тени, в роли которого выступают левая контурная образующая и горизонтальная прямая контура верхней плиты. Тень от контурной образующей, как и в предыдущем случае, совпадает с осью, а тень от профильно проецирующей прямой на цилиндрическую поверхность будет эллипсом, который проецируется в виде дуги окружности 1₂^т - 2₂^т.




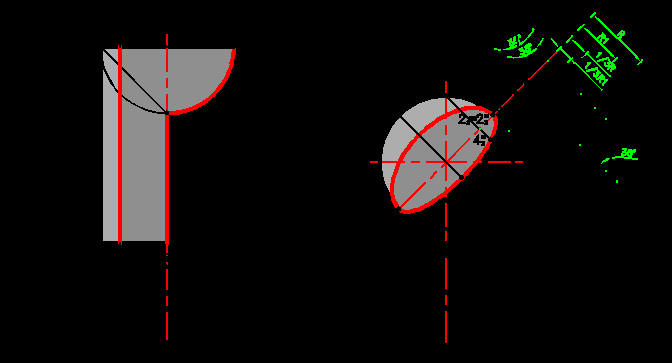
На рис.6.11 представлена сферическая ниша. После построения собственной тени строится падающая тень на внутреннюю поверхность сферы от участка контура ниши, являющегося контуром собственной тени. Таковой является дуга окружности 1 – 3 – 2. Для этого проводится замена плоскостей проекций. Вновь введенная плоскость параллельна световому лучу, поэтому направление луча на ней проецируется в натуральную величину 35^о. Тень от любой точки, лежащей на части контура, отбрасывающей тень, будет находиться на той же параллели, что и сама точка. Пересечение светового луча, проходящего через точку 3₃ контура ниши, с параллелью дает точку 3₃^т на контуре падающей тени. При возвращении в проекционной связи точки 3 на фронтальную плоскость проекций получается точка 3₂^т на контуре падающей тени. Аналогичным образом может быть построен ряд точек. Полученная кривая 1₂^т - 3₂^т - 4₂^т - 2₂^т является дугой эллипса. Расстояния от оси 1₂ - 2₂ до контура падающей тени составляют 1/3 от радиуса окружности соответствующей параллели. Зная это, достаточно лишь откладывать перпендикулярно прямой 1₂ - 2₂ расстояния, равные 1/3 радиуса соответствующей окружности.

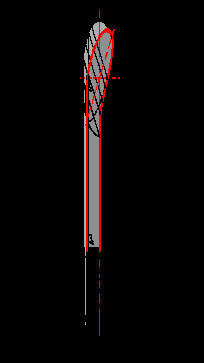
На рис.6.12 представлена комбинированная ниша, образованная цилиндрической и сферической поверхностями. Строится контур собственных теней 1₂^т - 2₂^т - 3₂^т для каждой из поверхностей. Затем строятся падающие тени на каждую из поверхностей. Контур 5₂^т - 6₂^т является падающей тенью от контура цилиндрической поверхности на саму цилиндрическую поверхность. Участок контура падающей тени 4₂^т - 5₂^т является тенью от контура сферы (дуги окружности) на цилиндрическую поверхность, который построен способом лучевых сечений. Лучевые сечения проведены через точки 7, 8, 9.

Тени в конической нише рассмотрены выше в разделе «Способ обратных лучей».


^ 6.8. Тени на лестнице


Падающие тени на ступенях лестницы возникают от ограждения, которое может быть ограничено горизонтальной и вертикальной плоскостями (рис.6.13) или горизонтальной, наклонной и вертикальной плоскостями (рис.6.14).

В первом случае тени будут возникать от двух прямых: фронтально проецирующей и горизонтально проецирующей. Сами ступени представляют собой фронтальные и горизонтальные плоскости уровня. Поэтому тени на подступенках от вертикальной прямой будут вертикальными прямыми, а от горизонтальной прямой – прямой под углом 45^о. Для построения используется профильная проекция. Тень полностью повторяет профильную проекцию ступеней.



В случае с наклонным ограждением, если его плоскость параллельна прямой, соединяющей ребра ступеней, тени на ступенях представляют собой зубцы, заключенные между двумя вертикальными прямыми. Эти вертикальные прямые являются падающей тенью на две мнимые наклонные плоскости Δ и Δ^/. Тени от остальных участков ограждения как в предыдущем случае.


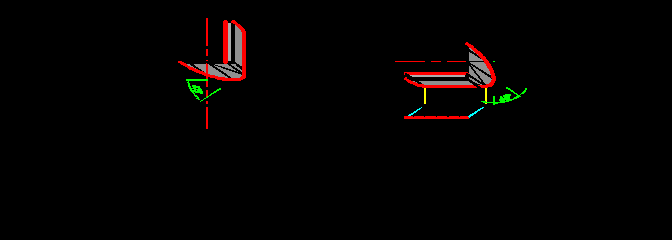
^ 6.9. Тени от кронштейнов


Формы, называемые кронштейнами, представляют собой цилиндрические поверхности с горизонтальными образующими. Сбоку поверхности ограничены параллельными плоскостями. Тени строятся с использованием профильной проекции.

На рис.6.15 представлен простой кронштейн. Касательным световым лучом на профильной проекции определяется точка 1₃, ограничивающая контур собственной тени. На фронтальной проекции через точку 3₂ проводится образующая, являющаяся контуром собственной тени. Далее определяется контур падающей тени от контурной образующей кронштейна, проходящей через точку 2. Участок кривой 2 – 1 будет отбрасывать тень на цилиндрическую поверхность кронштейна. Построения аналогичны построениям падающей тени в открытой цилиндрической нише.





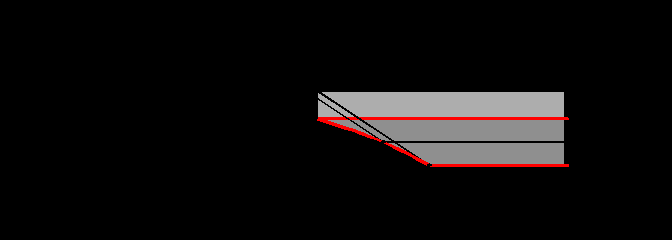
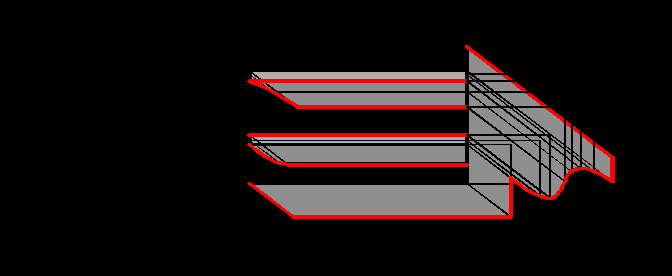
На рис.6.16 представлен кронштейн более сложной формы. Тени в верхней части кронштейна аналогичны предыдущему случаю. А в нижней выпуклой части контур собственной тени отбрасывает тень на вертикальную плоскость. Кроме того, построены также тени на стену способом «выноса».