12. ломаные и кривые линии (плоские и пространственные). Винтовая линия

Точку, прямую и плоскость называют элементарными геометрическими фигурами. Из них могут быть созданы все остальные геометрические фигуры.

Приняв в качестве элементарной фигуры точку, можно рассматривать любую линию как множество последовательных положений движущейся точки - траекторию точки.

Ломаная линия - линия, состоящая из отрезков прямой, расположенных в пространстве под некоторым углом друг к другу.

Кривые линии - могут быть плоскими, когда все точки кривой лежат в одной плоскости, и пространственными - когда точки кривой не лежат в одной плоскости.

К плоским кривым относятся кривые второго порядка: окружность, эллипс, парабола, гипербола, синусоида, циклоида и т.д. Прямая, лежащая в плоскости этих линий, может пересечь любую из них лишь дважды. С построением этих линий вы уже ознакомились при выполнении задания №1 "Геометрическое черчение" в курсе машиностроительного черчения.

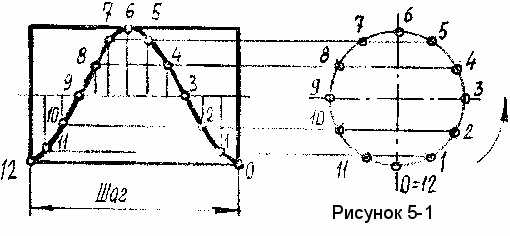
Из пространственных кривых наиболее часто встречается на практике цилиндрическая винтовая линия. Если точка совершает равномерное движение по прямой, которая в свою очередь совершает равномерное вращение вокруг параллельной ей оси, то она (точка) опишет пространственную кривую – цилиндрическую винтовую линию (рисунок 5-1).
^

13. КИНЕМАТИЧЕСКОЕ ОБРАЗОВАНИЕ КРИВЫХ ПОВЕРХНОСТЕЙ И ИХ ИЗОБРАЖЕНИЕ НА КОМПЛЕКСНОМ ЧЕРТЕЖЕ. классификация поверхностей

П
оверхность - множество точек, имеющее два измерения вдоль каких-либо линий этой поверхности.

В

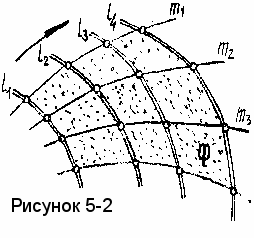начертательной геометрии пользуются, в основном, кинематическим способом образования поверхностей, т.е. движением линии (рисунок 5-2). Поверхность Ф представляет собой множество последовательных положений l1, l2, l3 и т.д. линии l , форма и движение которой подчинены некоторому закону. Линия l называется образующей. Линии, по которым она движется, называют направляющими –m1, m2, m3 и т.д.

Но в таком виде на чертеже поверхность обычно не задают.

Краткости и достаточной емкости геометрической информации о поверхности служат понятия определителя и ее каркаса.

Определитель поверхности - это минимальная, но достаточная информация о поверхности, необходимая для построения на ней любой ее точки.

Каркасом поверхности называют множество ее линий (например l и m, рисунок 5-2).

На комплексном чертеже поверхность обычно задают проекциями ее направляющих, и указывается способ построения ее образующих. Для придания чертежу большей наглядности строят на нем очерк поверхности.

Очерк поверхности - проекция ее контурной линии. Или иначе - это граница, отделяющая проекцию поверхности от остальной ч

асти плоскости.

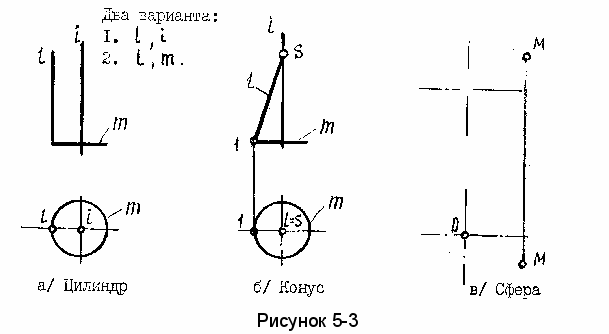
Примеры задания поверхностей вращения определителем представлены на рисунке 5-3.

П

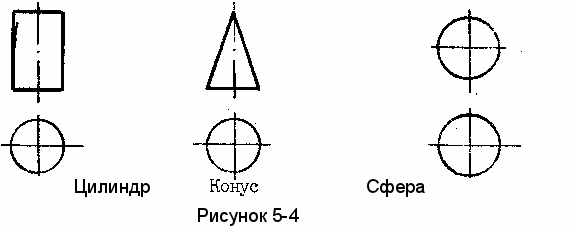
римеры чертежей поверхностей заданных очерком (рисунок 5- 4).

Для удобства изучения поверхностей их обычно делят на ряд классов. На примере поверхностей, которые встречаются в практике наиболее часто, рассмотрим эту классификацию.
^

13.1 Поверхности вращения

Это поверхности, которые описываются какой-либо линией при ее вращении вокруг неподвижной оси.

а) При вращении прямой образуются:

цилиндр вращения (прямая параллельна оси вращения);

конус вращения (прямая пересекается с осью вращения).

б) При вращении окружности образуется:

сфера (вращением окружности вокруг диаметра);
тор (вращением окружности вокруг оси, лежащей в

плоскости окружности, но не проходящей через ее центр);

в) При вращении кривой второго порядка образуются:

эллипсоид вращения (вращением эллипса);

параболоид вращения (вращением параболы);

однополостный гиперболоид;
2-х полостной гиперболоид.

13.2 Линейчатые поверхности

Это поверхности, описываемые какой -либо прямой (образующей) при ее движении в пространстве по какому-нибудь закону:

цилиндрическая поверхность (образуется движением прямой линии по некоторой кривой линии, при этом прямая имеет постоянное направление);

коническая поверхность (образуется движением прямой линии, проходящей через неподвижную точку, по некоторой кривой линии, называемой направляющей);
торс и т.д.

Если направляющая линия является ломаной линией, то образуются:

призматическая поверхность (образующая имеет постоянное направление);

пирамидальная поверхность (образующая проходит через неподвижную точку).

Имеются и более сложные линейчатые поверхности:

цилиндроид;

коноид;
косая плоскость и т. д.

Всякая прямая пересекается с такой поверхностью в двух точках, а плоскость пересекает ее по кривой второго порядка.
^

13.3 Поверхности второго порядка

коническая поверхность (конус вращения и эллиптический конус, получаемый деформацией параллелей конуса вращения в эллипсы);
цилиндрическая поверхность (цилиндр вращения, эллиптический, параболический и гиперболический цилиндры.

эллиптический цилиндр может быть получен из цилиндра вращения деформацией его параллелей в эллипсы);

эллипсоид (эллипсоид вращения, в частности сфера; трехосный эллипсоид, получаемый из эллипсоида вращения деформацией его параллелей в эллипсы);
параболоид, гиперболоиды и др.

13.4 Винтовые поверхности

Они описываются какой-либо линией (образующей) при ее винтовом движении. Если образующая винтовой поверхности прямая линия, то поверхность называется линейчатой винтовой поверхностью или геликоидом (пример – шнек). Различают прямой и наклонный геликоиды. В первом случае образующая во всех положениях перпендикулярна оси t, во втором - пересекает ось геликоида под постоянным углом отличным от прямого.
^

13.5 Циклические поверхности

ни описываются какой-либо окружностью (образующей) постоянного или переменного радиуса при ее произвольном движении.

К циклическим можно отнести все поверхности вращения и те из поверхностей второго порядка, которые имеют круговые сечения. Кроме этих к циклическим относят каналовые и трубчатые поверхности.

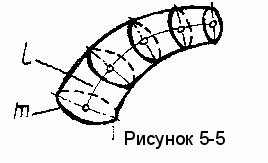
Каналовые поверхности (рисунок 5-5) образуются движением окружности переменного радиуса, центр которой 0 перемещается по заданной кривой (направляющей l ), а плоскость окружности остается перпендикулярной этой кривой.

Т ^
Рисунок 4-5
рубчатая поверхность образуется движением окружности постоянного радиуса – в этом ее отличие от каналовой поверхности.

13.6 Топографические поверхности

Образование их не подчинено какому-либо закону. К таким поверхностям относятся поверхности земной коры, корпуса судов, обшивки самолетов, автомобилей.

Н

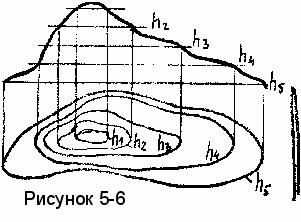а чертеже эти поверхности изображаются при помощи семейства некоторых линий (рисунок 5-6).

Из сказанного выше видно, что некоторые поверхности могут быть отнесены к нескольким классам одновременно

^

14. ВЗАИМОПРИНАДЛЕЖНОСТЬ ТОЧКИ И ПОВЕРХНОСТИ, ЛИНИИ И ПОВЕРХНОСТИ

Для построения точки на любой поверхности необходимо провести на этой поверхности произвольную линию и на ней взять точку.

В качестве такой вспомогательной линии следует брать графически простые линии, т.к. это упрощает решение.

На многогранных и линейчатых поверхностях в качестве вспомогательных линий лучше выбирать прямые линии, а на поверхностях вращения - окружности (параллели).

Для построения произвольной линии или фигуры, лежащей на поверхности, необходимо построить несколько точек этой фигуры (линии), а затем их последовательно соединить, учитывая при этом их принадлежность одной грани и видимость.

14.1 Построение линий на гранных поверхностях

Примеры построений представлены на рисунке 5-7. Пусть положение линий MN задано на видах спереди

Так как поверхности гранные, то линии MN в обоих случаях будут ломаными и точки излома принадлежат ребрам поверхностей, с которыми линии MN пересекаются на видах спереди. Такими точками являются точки 3 (в примере «а») и 2(в примере «б»). Эти точки на видах сверху находятся просто – способом принадлежности.

П
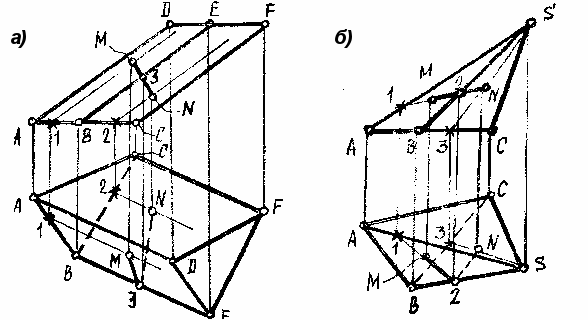
ример а) Для построения точек M и N проведем на поверхности призмы вспомогательные прямые параллельные боковым ребрам и проходящие через точки М и N. Эти прямые с помощью точек 1 и 2 несложно построить на виде сверху, а затем определить на них проекции точек М и N.

Рисунок 5-7

Полученные на виде сверху точки соединяем отрезками прямых. Участок М-3 принадлежит грани АВЕD, которая на виде сверху видима, следовательно и этот участок будет видимым. Участок 3-N принадлежит грани ВСFЕ которая на виде сверху невидима, следовательно отрезок 3-N так же будет невидимым.

Пример б) Построение линии МN на поверхности пирамиды так же начинаем с нахождения на виде сверху точки излома (т.2). Для построения точки М на поверхности пирамиды проведена вспомогательная прямая 1-2, принадлежащая грани АВS, а для нахождения т. N - линия S-3, принадлежащая грани ВСS. Точки 1 и 3 легко находятся на виде сверху, после чего построение точек М и N не вызывает затруднений.

14.2 Построение линий на поверхностях вращения

Примеры построений показаны на рисунке 5-8. Вид спереди этих линий задан. Необходимо достроить данные линии на видах сверху.

Пример а) Для построения линии АВ принадлежащей поверхности прямого кругового цилиндра в общем случае необходимо использовать горизонтали h или образующие l.

В

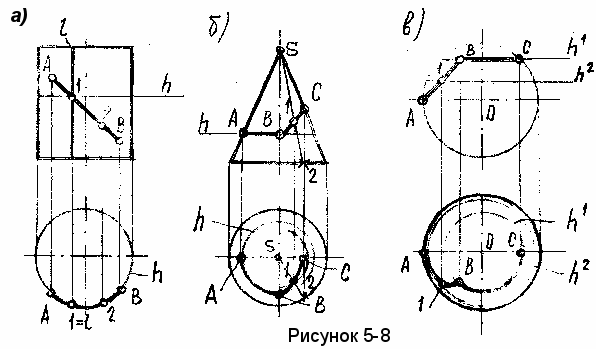
данном же случае целесообразно использовать вырожденный вид цилиндрической поверхности, где вся боковая поверхность цилиндра проецируется в окружность. Линия АВ при этом совпадает с окружностью и находится на передней ее части.

Пример б) Построение линии на поверхности конуса вращения начинаем с нахождения точек А и С, лежащих на контурных (очерковых) образующих конуса, которые на виде сверху находим без дополнительных построений.

Т.к. участок линии АВ параллелен основанию конуса, проводим через него горизонталь h (параллель).

Для построения участка ВС необходимо найти ряд дополнительных точек. Показано построение точки 2 при помощи образующей S-1 , но эту же точку можно построить и с помощью параллели (горизонтали) поверхности.

Пример в) Построение линии на поверхности сферы начато с нахождения точек А и С, лежащих на главном меридиане. Для построения участка линии ВС и промежуточной точки 1 использованы параллели поверхности (горизонтали h¹ и h²).

Blog

12. ломаные и кривые линии (плоские и пространственные). Винтовая линия

Содержание

ЛЕКЦИЯ №5