Муниципальное общеобразовательное учреждение

Вид материала

Документы

Содержание Ii. 1. поверхности вращения линейчатые 7 Общие сведения о кривых линиях I. 2. Пространственные кривые линии. Общие сведения о поверхностях вращения Ii. 1. поверхности вращения линейчатые Ii.1.1. конус Ii.1.2. цилиндр Ii.1.3. однополостный гиперболоид Ii.2. поверхности вращения нелинейчатые Ii.2.3. эллипсоид, двухполостный гиперболоид, параболоид, поверхность вращения общего вида II. 3. Поверхности вращения с плоскостью параллелизма. II.4.Поверхности, задаваемые каркасом. Практическое применение поверхностей вращения в различных сферах деятельности человека В архитектуре Гауди, Ле Корбюзье 1963 году в порту города Кобе В астрономии В технике – электронике 4. В механике 1. Краткое описание устройства оборудования ... Полное содержание

Подобный материал:

• Муниципальное общеобразовательное учреждение, 999.25kb.
• Муниципальное общеобразовательное учреждение, 515.34kb.
• Публичный доклад, 1547.48kb.
• Муниципальное общеобразовательное учреждение, 822.73kb.
• Муниципальное автономное общеобразовательное учреждение, 794kb.
• Муниципальное общеобразовательное учреждение, 908.15kb.
• Приказ № от 2011г. Рабочая программа учебного предмета Муниципальное общеобразовательное, 767.15kb.
• Муниципальное автономное общеобразовательное учреждение, 282.06kb.
• Департамент образования г. Братска муниципальное общеобразовательное учреждение лицей, 738.03kb.
• Департамент образования г. Братска муниципальное общеобразовательное учреждение лицей, 1002.75kb.

Муниципальное общеобразовательное учреждение

"Гимназия искусств при главе администрации МР "Сосногорск"





Выполнила: Зуева Оксана, ученица 10 класса

Руководитель: учитель математики

Кривенко Ольга Владимировна


Сосногорск 2009

ОГЛАВЛЕНИЕ

ПРИЛОЖЕНИЯ……………………………………………………………… - 22-

СПИСОК ЛИТЕРАТУРЫ …………………………………………………... – 34-

ВВЕДЕНИЕ

Кривые линии и поверхности вращения занимают особое положение в начертательной геометрии. Так, как учебная программа касается темы моей работы только частично, поверхностно, но я бы хотела более глубже и подробнее изучить раздел геометрии: вращающиеся поверхности, кривые линии и тела вращения и найти область, где можно применить эти знания.

Используя линии, можно создать наглядные модели многих процессов и проследить их течение во времени. Линии позволяют установить и исследовать функциональную зависимость между различными величинами.

С помощью линий удаётся решать многие научные и инженерные задачи, решение которых аналитическим путём часто приводит к использованию чрезвычайно громоздкого математического аппарата. Геометрическая интерпретация удобна и доступна для подавляющего большинства людей, т.к. с её использованием алгебраические задачи перестают быть абстрактными. Геометрический образ откладывается в сознании легче, и позволяет решать задачи, которые аналитическим путем решить очень сложно.

Линии широко используются при конструировании поверхностей различных технических форм.

Применение знаний о кривых линиях и поверхностях вращения в производственных технологических процессах приводит к значительной экономии энергетических и топливных ресурсов.

Цель работы: изучить данный раздел геометрии более подробно. Найти области применения «Кривых линий и поверхностей вращения» на практике: в решении геометрических и инженерных задач, в архитектуре, в производственных технологических процессах.

Для достижения этих целей я поставила перед собой следующие задачи:

• Изучить теоретический материал;
  
• Выделить те области, где могут быть применены кривые линии и поверхности вращения;
  
• Подробно исследовать применение данных понятий в производственных процессах промышленного предприятия нашего города – ТЭЦ.
  

1. ^ ОБЩИЕ СВЕДЕНИЯ О КРИВЫХ ЛИНИЯХ
   

I. 1. Плоские кривые линии

Кривая линия – это траектория перемещающей точки. Если кривая линия совмещается всеми точками с плоскостью, её называют плоской. Порядком плоской алгебраической кривой считают максимальное число точек её пересечения с прямой линией. К плоским кривым относят все кривые второго порядка. На рис.1 показано построение этих кривых и приведены их канонические уравнения.

Эллипсом является геометрическое место точек М, для которых сумма расстояний до точек F1 и F2 плоскости постоянна и равна большой оси АВ (рис. 1, а). Точки F1 и F2 называют фокусами. Построим точку, принадлежащую эллипсу, если даны фокусы F1, F2 и вершины А, В. Для этого на оси АВ берём произвольную точку L и из фокуса F проводим дугу окружности радиусом АL. Затем из фокуса F2 чертим дугу радиусом ВL, пересекающую первую дугу в точке М. Таким образом, F1M + F2M = АВ.

При равных осях эллипс превращается в окружность , являющуюся геометрическим местом точек плоскости, равноудалённых от данной точки О (рис. 1, б).

Параболой является геометрическое место точек М, для которых расстояния до точки F плоскости и до прямой KN, не проходящей через точку F, равны

(рис. 1, в). Вершина О параболы делит расстояние от точки F до прямой KN пополам. Точку F называют фокусом, прямую KN – директрисой. Построим точку М, принадлежащую параболе, если дан фокус F и директриса KN. Для этого проводим прямую LM // KN и из точки F засекаем её дугой окружности радиусом MN. Итак, MN = MF.

Гиперболой является геометрическое место точек М, для которых разность расстояний до точек F1 и F2 плоскости постоянна и равна расстоянию между вершинами А и В кривой (рис. 1, г). Точки F1 и F2 называют фокусами, ось Х – действительной осью, а Y – мнимой.
^

I. 2. Пространственные кривые линии.

Если кривую линию без её деформации нельзя совместить всеми точками с плоскостью, то её называют пространственной. К таким кривым относят винтовые линии.

Винтовая линия – это траектория движения точки, равномерно перемещающейся вдоль образующей, которая равномерно вращается вокруг оси этой поверхности. Винтовую линию называют правой, если на видимой стороне поверхности она идёт слева вверх направо (рис. 2, а); в противном случае её называют левой (рис. 2, б). Расстояние S, которое проходит точка вдоль образующей за один её оборот, называют шагом винтовой линии. Построение всех винтовых линий однотипно.

2. ^ ОБЩИЕ СВЕДЕНИЯ О ПОВЕРХНОСТЯХ ВРАЩЕНИЯ
   

Поверхность – это геометрическое место линии, движущейся в пространстве по определённому закону. Эту линию называют образующей. Она может быть прямой, тогда образованную ей поверхность относят к классу линейчатых. Если образующая – кривая линия, поверхность считают нелинейчатой. Линию, по которой перемещают образующую, называют направляющей. В качестве последней иногда используют след поверхности.

Определителем поверхности называют совокупность условий, задающих поверхность в пространстве. На чертеже поверхность вращения задается своим очерком. Очерком поверхности называются линии, которые ограничивают области ее проекций.

Поверхность считают заданной, если можно построить проекции любой её образующей. Одну и ту же поверхность можно образовать движением различных линий. Например, при вращении каждая точка образующей описывает окружность, плоскость которой перпендикулярна оси. Соответственно, линия пересечения поверхности вращения плоскостью, перпендикулярной оси, является окружностью. Такие окружности называют параллелями (рис. 3). Параллель наибольшего радиуса называют экватором, наименьшего - горлом.

    Плоскость, проходящую через ось поверхности вращения, называют меридиональной, линию ее пересечения с поверхностью вращения - меридианом. Меридиан, лежащий в плоскости, параллельной плоскости проекций, называют главным меридианом. Например, свойством сдвигаемости, состоящим в том, что поверхность вращения может, вращаясь вокруг оси, сдвигаться без деформации вдоль самой себя. Меридиан поверхности вращения является кратчайшей (или геодезической) линией поверхности. Параллели и меридианы, пересекаясь под прямыми углами, образуют ортогональную сеть на поверхности вращения, аналогично прямоугольной декартовой сети на плоскости.

Поверхности вращения – это поверхности созданные при вращении образующей m вокруг оси i (рис.4).

Геометрическая часть определителя состоит из двух линий: образующей m и оси i (рис. 4).

Алгоритмическая часть включает две операции:

1. на образующей m выделяют ряд точек A, B, C, …F,

2. каждую точку вращают вокруг оси i. (рис. 4)

Так создается каркас поверхности, состоящей из множества окружностей, плоскости которых расположены перпендикулярно оси i (рис.4).

Из закона образования поверхности вращения вытекают два основных свойства:

1. Плоскость перпендикулярная оси вращения, пересекает поверхность по окружности – параллели.

2. Плоскость, проходящая через ось вращения, пересекает поверхность по двум симметричным относительно оси линиям – меридианам.

Рассмотрим наиболее распространенные поверхности вращения с криволинейными образующими:

Сфера – образуется вращением окружности вокруг её диаметра (рис.5).

При сжатии или растяжении сферы она преобразуется в эллипсоиды, которые могут быть получены вращением эллипса вокруг одной из осей: если вращение вокруг малой оси, то эллипсоид называется сжатым или сфероидом (рис.6), если вокруг большой – вытянутым (рис.7).

Тор – образуется при вращении окружности вокруг оси, не проходящей через центр окружности (рис.8).

Параболоид вращения – образуется при вращении параболы вокруг своей оси (рис.9).

Гиперболоид вращения – различают одно (рис.10 а) и двух (рис.10 б) полостной гиперболоиды вращения. Первый получается при вращении вокруг мнимой оси, а второй – вращением гиперболы вокруг действительной оси.

^

II. 1. ПОВЕРХНОСТИ ВРАЩЕНИЯ ЛИНЕЙЧАТЫЕ

Все поверхности этого класса образованы вращением прямой линии вокруг другой прямой. Две прямые могут занимать относительно друг друга три различных положения. Каждому из них соответствует своя поверхность вращения.

^ II.1.1. КОНУС

Конус (прямой круговой) — это тело, ограниченное поверхно­стью вращения равнобедренного треугольника вокруг его оси симметрии (рис. 11). Поверх­ность конуса состоит из круга (основания) и бо­ковой поверхности. Вершину конуса можно со­единить с любой точкой окружности основания образующей — отрезком, лежащим на боковой поверхности. Высота конуса — расстояние от вершины до основания. Сечение боковой поверх­ности плоскостью, параллельной основанию, — окружность. Конус образуют вращением прямой OD вокруг пересекающейся с ней оси Z (рис. 12). Координатные плоскости XOZ и YOZ рассекают конус по пересекающимся прямым OD, OE, OK и OF; плоскость XOZ даёт в сечении точку О; плоскость, параллельная XOY, пересекает по окружности (DFEK). Для построения точки, принадлежащей кривой поверхности, её поверхности располагаем на проекциях линии, лежащей на этой поверхности.

Усеченный конус — это часть конуса, заключенная между его основанием и сечением, параллельным основанию (рис. 13). Усеченный конус можно рассматривать как результат вращения равнобедренной трапеции вокруг ее оси симмет­рии. При вращении основания трапеции описыва­ют круги — основания усеченного конуса. Вы­сота усеченного конуса — это расстояние меж­ду основаниями.

^ II.1.2. ЦИЛИНДР

Цилиндр (прямой круговой) — это тело, ограниченное поверхностью вращения прямоугольника вокруг прямой, проходящей через противоположные стороны (рис. 14). Поверхность цилиндра состоит из двух кругов (ос­нований) и боковой поверхности. Плоскости ос­нований параллельны, расстояние между ними - высота цилиндра. Ось цилиндра — это поверхность состоит из образующих — равных отрезков, параллельных оси. Боковую поверхность можно развернуть на плос­кость — получится прямоугольник. Главным меридианом цилиндрической поверхности являются две параллельные прямые. (Рис 15). Цилиндр образуют вращением прямой ЕD вокруг параллельной ей оси Z (рис. 16) Плоскости XOZ и YOZ пересекают его по параллельным прямым ED, FK, NP, LM, а плоскость XOY и ей параллельные – по окружностям DPKM и (ENFL).

^ II.1.3. ОДНОПОЛОСТНЫЙ ГИПЕРБОЛОИД

Однополостный гиперболоид образуют вращением прямой ED вокруг скрещивающейся с ней оси Z (рис. 17).

Плоскости XOZ и YOZ пересекают его по гиперболам FK, LM, PQ и RS, а плоскость XOY и ей параллельные – по окружностям (GU, FPLR и KQMS). При вращении точек D и Е их проекции d и е перемещаются по окружности, а проекции d и e – по прямым, параллельным оси Х. Точка U прямой DE, ближе других расположенная к оси вращения, описывает окружность UU1 наименьшего диаметра. Эту окружность называют горлом поверхности. Лучи, проектирующие какую-либо поверхность, касаются её в точках, образующих контурную линию. Соответствующая проекция этой линии называется очерком поверхности.
^

II.2. ПОВЕРХНОСТИ ВРАЩЕНИЯ НЕЛИНЕЙЧАТЫЕ

К этому классу относят в основном поверхности, образованные вращением кривых второго порядка.

II.2.1. СФЕРА и ШАР

Сфера — это множество точек в пространстве, равноудаленных от фик­сированной точки (центра сферы). Сферу образуют вращением окружности вокруг её диаметра (рис. 18). Любая плоскость пересекает сферу по окружности. Очерк фронтальной проекции сферы называют главным меридианом, очерк горизонтальной проекции – экватором. Проекции точки К, лежащей на поверхности сферы, принадлежат проекциям горизонтальной окружности, проведённой на сфере (Рис. 19). Радиус сферы — расстоя­ние от центра до любой точки сферы, диаметр — длина отрезка, соединяющего две точки на сфе­ре и проходящего через центр. Диаметр равен двум радиусам. Иногда радиусом и диаметром называют сами отрезки. Плоскость в пространстве либо не имеет об­щих точек со сферой, либо имеет одну общую точку (точку касания), либо пересекается по окружности. Касательная к сфе­ре плоскость перпендикулярна радиусу, прове­денному в точку касания.

Сегмент­ная поверхность — это часть сферы, отсекаемая плоскостью.

Шар — это тело, ограниченное сферой (рис. 18); его можно рассматривать как результат вращения круга вокруг его диаметра. Плоские сечения шара представля­ют собой круги, наибольший из которых прохо­дит через центр шара (большой круг).

Шаровой сегмент — эта часть шара, отсе­ченная от него плоскостью (рис. 20). Шаровой сектор — это тело вращения плос­кого кругового сектора вокруг его оси симмет­рии (рис. 21). Шаровой сектор можно составить из конуса и шарового сегмента. Полная поверх­ность шарового сектора состоит из сегментной поверхности и боковой поверхности конуса. Шаровой слой — это часть шара, вырезаемая из него двумя параллельными плоскостями (рис. 22).

II.2.2. ТОР

Круговой тор (рис. 23) образуют вращением окружности вокруг оси, лежащей в плоскости этой окружности и не являющейся её диаметром. Таким образом, сферу можно рассматривать как частный случай тора. Различают тор-кольцо, когда ось вращения не пересекает образующую окружность, и тор-бочку.

В радиотехнике используют также параболический и эллиптический тор.

Параболический тор образуют вращением параболы вокруг прямой, лежащей в плоскости этой параболы и не являющейся её фокальной осью.

Эллиптический тор образуют вращением эллипса вокруг прямой, лежащей в плоскости этого эллипса и не являющейся его осью.

^ II.2.3. ЭЛЛИПСОИД, ДВУХПОЛОСТНЫЙ ГИПЕРБОЛОИД, ПАРАБОЛОИД, ПОВЕРХНОСТЬ ВРАЩЕНИЯ ОБЩЕГО ВИДА

Эллипсоид образуют вращением эллипса вокруг его малой или большой оси. В первом случае получают сжатый (рис. 24, а), а во втором – вытянутый эллипсоиды вращения (рис. 24, б). Плоскости XOZ и YOZ пересекают их по эллипсам DE и EF, а плоскость XOY – по окружности DF.

Двуполостный гиперболоид образуют вращением гиперболы DE вокруг её действительной оси FF1 (рис. 25). Плоскости XOZ и YOZ пересекают его по гиперболам DE и KE; плоскость XOY даёт в сечении мнимую точку О.

Параболоид образуют вращением параболы OD вокруг её фокальной оси OF (рис. 26).

Поверхность вращения общего вида образуют вращением произвольной кривой.
^

II. 3. Поверхности вращения с плоскостью параллелизма.

Все поверхности этого класса – линейчатые.

1. Цилиндроид образуют перемещением прямой по двум кривым направляющим, когда образующая остаётся параллельной заданной плоскости.

2. Коноид образуют перемещением прямой по кривой линии и прямой, когда образующая остаётся параллельной заданной плоскости. Частным случаем коноида является прямой геликоид, образуемый перемещением прямой по винтовой линии и её оси, когда образующая остаётся параллельной заданной плоскости.

3. Гиперболический параболоид или косую плоскость образуют перемещением прямой по двум скрещивающимся прямым, когда образующая остаётся параллельной некоторой плоскости. Получаемая поверхность имеет седлообразную форму (рис. 27). Плоскости XOZ и YOZ пересекают эту поверхность по параболам OD и OE; плоскости параллельные XOZ и YOZ ,также дают в сечении параболы; плоскость XOZ пересекает поверхность по двум пересекающимся прямым OL и OK, а плоскости, параллельные XOZ,- по гиперболам (EN и DM).
^

II.4.Поверхности, задаваемые каркасом.

К ним относятся поверхности, образование которых не подчинено определённому геометрическому закону. Эти поверхности задают каркасом – семейством линий, принадлежащих им и параллельных координатным плоскостям (рис. 28). На рис. 28 изображён объёмный график, используемый в радиотехнике. Поверхность определена кривыми линиями, одно семейство которых (CD) параллельно плоскости XOZ, а другое (АВ) – плоскости YOZ. Точка М поверхности определена как точка пересечения кривых АВ и CD.

3. ^ ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ ПОВЕРХНОСТЕЙ ВРАЩЕНИЯ В РАЗЛИЧНЫХ СФЕРАХ ДЕЯТЕЛЬНОСТИ ЧЕЛОВЕКА
   

Поверхности вращения обладают некоторыми важными свойствами, используемыми в процессе конструирования деталей различных машин и механизмов.

1. ^ В АРХИТЕКТУРЕ
   

Одним из самых ярких примеров применения вращающихся поверхностей в архитектуре являются гиперболоидные конструкции. Гиперболоидные конструкции - сооружения в форме гиперболоида вращения или гиперболического параболоида. Такие конструкции, несмотря на свою кривизну, строятся из прямых балок. Однополостный гиперболоид и гиперболический параболоид — дважды линейчатые поверхности, то есть через любую точку такой поверхности можно провести две пересекающиеся прямые, которые будут целиком принадлежать поверхности. Вдоль этих прямых и устанавливаются балки, образующие характерную решётку. Такая конструкция является жёсткой: если балки соединить шарнирно, гиперболоидная конструкция всё равно будет сохранять свою форму под действием внешних сил.

Гиперболоидную форму конструкций ввёл в архитектуру В. Г. Шухов. Первая в мире стальная сетчатая башня в форме гиперболоида вращения была построена Шуховым для крупнейшей дореволюционной Всероссийской промышленной и художественной выставки в Нижнем Новгороде, проходившей с 28 мая (9 июня) по 1 (13) октября 1896 года (рис. 29).

Дальнейшей модификацией идеи сетчатых гиперболоидных конструкций стала конструкция радиобашни на Шаболовке в Москве (рис. 30), построенной Шуховым в 1919—1922 гг. Первоначальный проект высотой 350 м из-за дефицита металла был заменен на 150-метровый вариант, который эксплуатируется и поныне. В течение своей жизни Шухов построил более двухсот гиперболоидных башен различного назначения.

Гиперболоидные конструкции впоследствии строили многие великие архитекторы: ^ Гауди, Ле Корбюзье, Оскар Нимейер.

Гиперболоидные шуховские башни востребованы и в настоящее время. В ^ 1963 году в порту города Кобе в Японии по проекту компании Nikken Sekkei была построена 108-метровая гиперболоидная шуховская башня (Kobe Port Tower) (рис. 31). В 1968 году в Чехии по проекту архитектора Карела Хубачека была построена гиперболидная башня «Йештед» высотой 100 метров (Рис. 32). В 2003 году была построена гиперболоидная башня Шухова в Цюрихе. Авторы башни — архитекторы Даниэль Рот и Александр Ком (Daniel Roth, Alexander Kohm). Идеи гиперболоидных конструкций башен Шухова известный архитектор Михаил Посохин предложил использовать при проектировании новых небоскрёбов в деловом центре «Москва-Сити». 610-метровая гиперболоидная сетчатая шуховская башня возводится с ноября 2005 года в Гуанчжоу в Китае компанией Arup (рис. 33).

2. ^ В АСТРОНОМИИ
   

Решение Керра приводит к наличию так называемого конуса выхода. С помощью этого воображаемого конуса удобно разделять световые лучи на способные покинуть звезду и на те лучи, которые она от себя не отпускает. Уйти в окружающую Вселенную удается только тем лучам, которые испущены с поверхности звезды под углами, заключенными во внутренней части конуса выхода (рис. 34). Таким образом, при использовании данной поверхности вращения легко определить какие лучи звезды, достигают поверхности Земли, а какие пролетают мимо.

3. ^ В ТЕХНИКЕ – ЭЛЕКТРОНИКЕ
   

В этой области самое широкое применение поверхностей вращения. Конус участвует в образовании формы диаграммы направленности антенны, антенны и её облучателя, диффузора громкоговорителя, резонатора, отражателя радиоволн, электроннолучевых трубок и электронных ламп, световода, деталей вакуумных установок и так далее. Цилиндр применяют при образовании формы волноводов, антенн, амортизаторов приборов, зеркал лазеров, корпусов датчиков и так далее. Сфера образует форму диаграммы направленности антенн, обтекателя и излучателя антенны, головки микрофона, контактов реле и так далее. Торовые поверхности имеют диаграммы направленности антенн, поверхности положения объекта в пространстве, антенны и их обтекатели, волноводы, резонаторы, громкоговорители и так далее. Форму эллипсоида имеют зеркала антенн и лазеров, излучатели антенн, поверхности положения и так далее. С применением знаний о поверхностях вращения на практике ученые-техники далеко продвинулись вперед, тем самым расширяя возможности средств связи.

^ 4. В МЕХАНИКЕ

Конические катушки используются в линиях механизированной намотки электрических машин и аппаратов. Катушки изготавливаются из ударопрочного полистирола или полипропилена и предназначены для намотки эмалированных и других обмоточных проводов: круглых диаметром до 4 мм и прямоугольных сечением до 30 мм².

Конические роликоподшипники (рис. 35) имеют логарифмический профиль дорожек качения, что обеспечивает оптимальное распределение напряжений в зоне контакта ролики/дорожки качения колец. Особая геометрия поверхностей вращения направляющих бортов и больших торцов роликов способствует образованию смазывающей пленки между торцами роликов и бортами колец подшипников в зоне их контакта. Перечисленные преимущества обеспечивают повышенную эксплуатационную надежность подшипников и меньшую чувствительность к перекосам.

  Сферические роликоподшипники (рис. 36) являются очень надежными и имеют два ряда роликов, общую сферическую дорожку качения на наружном кольце и две дорожки качения на внутреннем кольце, расположенных под углом к оси подшипника, что обеспечивает подшипнику большую грузоподъемность. Это удачное конструктивное решение делает данные подшипники незаменимыми для многих особо требовательных случаев применения. Подшипники являются самоустанавливающимися, поэтому они нечувствительны к перекосам вала относительно корпуса, прогибам и отклонениям. Сферические роликоподшипники главным образом используются в бумагоделие, металлургической, нефтяной и горнодобывающей промышленности, а также в других областях тяжелого машиностроения.

4. ПРИМЕНЕНИЕ ПОВЕРХНОСТЕЙ ВРАЩЕНИЯ в производственных процессах СОСНОГОРСКОЙ ТЭЦ
   

Свои исследования я связала с работой Сосногорской ТЭЦ, т.к. вся система водоснабжения связана с телами вращениями их свойствами. Я провела следующие исследования:

1. Изучила описание устройства оборудования центральной насосной станции, а также характеристику градирен СТ.NN1,2;
   
2. Ознакомилась с конструкцией теплопроводов, туб и их соединений;
   
3. Рассмотрела, какие поверхности вращения используются в этой сфере.
   

^ 1. КРАТКОЕ ОПИСАНИЕ УСТРОЙСТВА ОБОРУДОВАНИЯ

ЦЕНТРАЛЬНОЙ НАСОСНОЙ СТАНЦИИ.

Для охлаждения циркуляционной воды, ввиду ограниченной возможно­сти использования прямоточной системы, на Сосногорской ТЭЦ сооружена оборотная схема водоснабжения.

Кроме того, путем переключений в колодцах турбина может быть подключена как к прямоточной схеме, так и к оборотной схеме водоснабжения. Схема оборотного водо­снабжения принята трехниточная, т.е. состоит из 3-х напорных и 3-х сливных водоводов. В железобетонном здании центральной насосной станции установлены циркуляционные насос. В систему оборотного водоснабжения входят две градирни, имеющие форму усеченного конуса, с площадью орошения 2100 м² типа БГ-2100-70-Н. В градирни поступает для охлаж­дения вода с температурой слива с конденсаторов турбин. С помощью водораспределительного устройства вода поступает на ороситель, далее в виде мелких капель-пленок движется сверху вниз через оросительное устройство. Вытяжная башня и разность удельных весов между наружным более холодным и подогретым в градирне воздухом создают тягу и обес­печивают непрерывное поступление внутрь градирни наружного воздуха, который движется через оросительное устройство навстречу движению воды. В результате в водосборный резервуар (чашу) вода поступает с пониженной температурой. Охлаждение воды в градирне происходит в результате совместного действия в основном 2-х процессов: теплоотда­чи соприкосновением воды с более холодным воздухом и поверхностным испарением с водяной пленки и капель.

Теплоотдача соприкосновением воды с воздухом осуществляется благодаря наличию разности температур воды и воздуха.

Испарение является результатом наличия разности парциальных давлений пара у поверхности водяной пленки и в основной массе про­ходящего через ороситель воздуха.

При положительных температурах атмосферного воздуха (летом) преобладающая роль в охлаждении воды до 90% в градирне происходит на долю испарения, при отрицательной (зимой) до 60% - на долю теплоотдачи соприкосновением.

Подготовленная охлажденная вода из водосборного бассейна (чаши) градирни по 2-м трубопроводам Ф1600 мм через решетки поступает в водоприемные камеры, которые между собой соединены. Из водоприемных камер вода циркуляционными насосами по трем напорным трубопроводам Ф1400 мм подается в конденсаторы турбин, где, забирая тепло от­работанного пара, подогревается на 8-23 град.С и по трем сбросным водоводам Ф1400 мм поступает в градирню через водораспределительный стояк. Из стояка по магистральным и рабочим трубопроводам разбрыз­гивается соплами и падает вниз на ороситель.

^ 2. ОПИСАНИЕ КОНСТРУКЦИИ, КРАТКАЯ ХАРАКТЕРИСТИКА

БАШЕННЫХ ГРАДИРЕН СТ.NN1,2.

(Рис. 37) Водосборный бассейн градирни представляет вид чаши с запа­сом воды.

Водораспределительное устройство:

(Рис. 38) В центре бассейна расположен монолитный водораспределитель­ный стояк (цилиндрической формы), разделенный перегородкой на две части, к каждой из которых проведен напорный трубопровод теплой воды. Это дает возможность при отключении одной из частей стояка уменьшить рас­ход воды и плотность орошения градирни в 2 раза.

От стояка радиально отходят магистральные напорные трубопро­воды к которым относительно окружности подсоединены рабочие трубы с разбрызгивающими соплами с чашечными отражателями.

Вытяжная башня изготовлена из крупноразмерных деревянных щитов в виде усеченного конуса и состоит из 6 яру­сов по высоте (А, Б, В, Г, Д, Е).

Оросительное устройство состоит из несущего железобетонного каркаса, собственно одноярусного оросителя (деревянных блоков) и ветровых перегородок. Компоновка оросителя выполнена по радиально­секторной схеме.

2.2. Характеристика башенных градирен ст.NN1,2.

Тип........................................БГ-2100-70-Н

Площадь орошения (м2)......................2100

Вытяжная башня:

- диаметр вверху (м).......................31

- диаметр внизу (м)........................51

- высота (м)...............................65

Ороситель:

- максимальная плотность орошения при температурном перепаде 10 град.С (м3/час м2)...........10,5

- минимальная плотность орошения при температурном перепаде 11 град.С (м3/час м2).......4,5

Максимальная производительность градирни (м3/час)...................22000

Минимальная производительность градирни (м3/час)...................9450


Тепловая сеть - это система прочно и плотно соединенных между собой участников теплопроводов, по которым теплота с помощью теплоносителей (пара или горячей воды) транспортируется от Сосногорской ТЭЦ к тепловым потребителям Сосногорского района.

3. Конструкция теплопроводов.

(Рис. 39) Теплопровод является цилиндром, т.е. одной из форм вращающихся поверхностей. В Сосногоркой ТЭЦ теплопровод состоит из трех основных элементов:

· рабочего трубопровода, который служит для транспортировки теплоносителя и который в современных условиях обычно выполняется из стальных труб круглого сечения, соединенных между собой с помощью сварки;

· изоляционной конструкции, предназначенной для защиты наружной поверхности стального трубопровода от коррозии и теплопровода в целом от тепловых потерь;

· несущей конструкции, воспринимающей всю весовую нагрузку и другие усилия, возникающие при его работе, а также разгружающей стальной трубопровод и его изоляционную конструкцию от нагрузки окружающей среды (веса грунта движущегося наземного транспорта, ветра и т. д.).

4. Трубы и их соединения.

(Рис. 40) В настоящее время для сооружения тепловых сетей на Сосногорской ТЭЦ применяются, стальные трубы круглого сечения, изготовленные из, так называемой, спокойной стали для транспорта теплоносителя с любой температурой от 0^ОС до 150, но при различных давлениях.

Основные типы стальных труб, применяемых для тепловых сетей Сосногорской ТЭЦ имеют следующие характеристики:

- диаметром до 400 мм включительно - бесшовные, горячекатаные;

- диаметром выше 400 мм - электросварные с продольным швом и электросварные со спиральным швом.

Трубы для тепловых сетей изготавливаются главным образом из стали следующих марок:, стали 10, 20,

Трубопроводная арматура - это элементы трубопровода, необходимые для соединения отдельных труб между собой, их ответвления от основной ветви, переходов с одного диаметра к другому и т. п.

 1. Фланец - плоский диск из металла с отверстием различной формы (круг) внутри и отверстиями по внешней стороне для дальнейшего соединения, предварительно соединенный к трубе, и предназначенный для соединения этих труб, с помощью крепежных деталей между собой. Фланец является плоской торовой поверхностью вращения (рис. 41).

2. Отводы предназначены для ответвления, изменения направления движения жидкости по трубопроводу. Представляют из себя гнутую трубу с внутренним диаметром, равным ДУ подсоединяемой трубы. Чаще всего выполнены под сварку, с одинаковым диаметром на входе и выходе. Большинство отводов изготавливают из низколегированной или углеродистой стали. Иногда из высоколегированной и высокостойкой. Выбор материала во многом зависит от технологического процесса изготовления. )

3. Переходы служат для соединения двух труб с различным внутренним условным диаметром.

4. Заглушки применяются с целью заглушения труб трубопровода при ремонте, а также могут устанавливаться в конце ветвей трубопровода.  

Схема трубопроводов, размещение опор и компенсирующих устройств выбраны таким образом, чтобы суммарное напряжение от всех одновременно действующих нагрузок ни в одном сечении трубопровода не превосходило допускаемого. Заглушки являются половиной сферы. (Рис. 43) Таким образом, благодаря форме данных конструкций  которые являются в некотором роде телами вращения достигаются ускорения технологических процессов и приводит к максимально низкой затрате энергии и ресурсов.


Заключение

В ходе своего исследования я изучила теоретический материал из дополнительных источников; побывала на экскурсии на ТЭЦ, где получила более подробные сведения об использовании кривых линий и поверхностей вращения в производстве; изучила техническую литературу, касающуюся производственных процессов на Сосногорской ТЭЦ и пришла к выводу, что применение знаний о кривых линиях и поверхностях вращения в производственных технологических процессах приводит к значительной экономии энергетических и топливных ресурсов, а также модернизирует и ускоряет

Я пришла к выводу, что «Кривые линии и Поверхности вращения» не только выделяются отдельной главой в математике, но и имеют обширное применение в архитектуре и на промышленных предприятиях, что является неотъемлемой частью нашей жизни, а так же применение знаний о кривых линиях и поверхностях вращения в производственных технологических процессах приводит к значительной экономии энергетических и топливных ресурсов.


ПРИЛОЖЕНИЯ





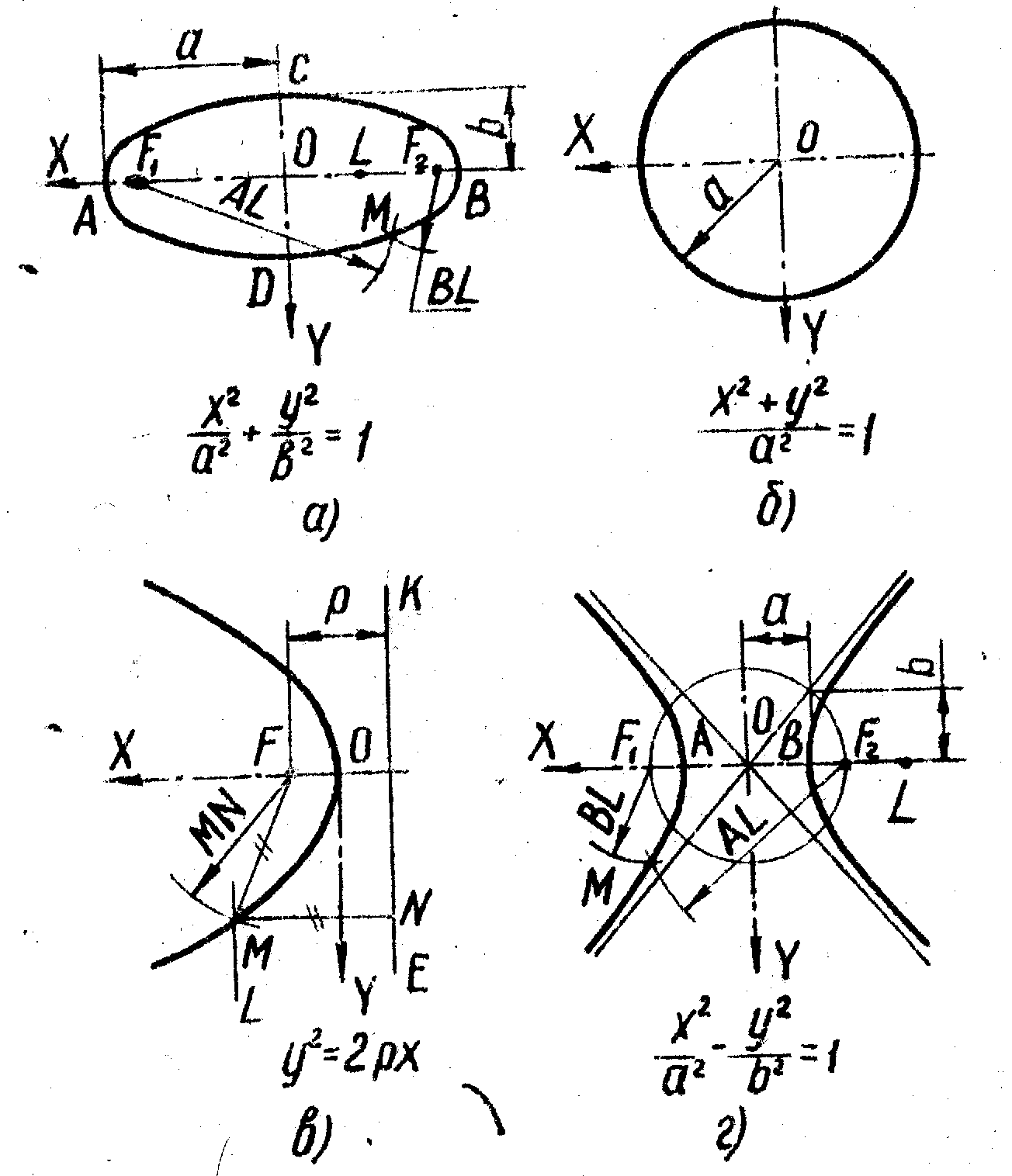
Рис. 1


Р
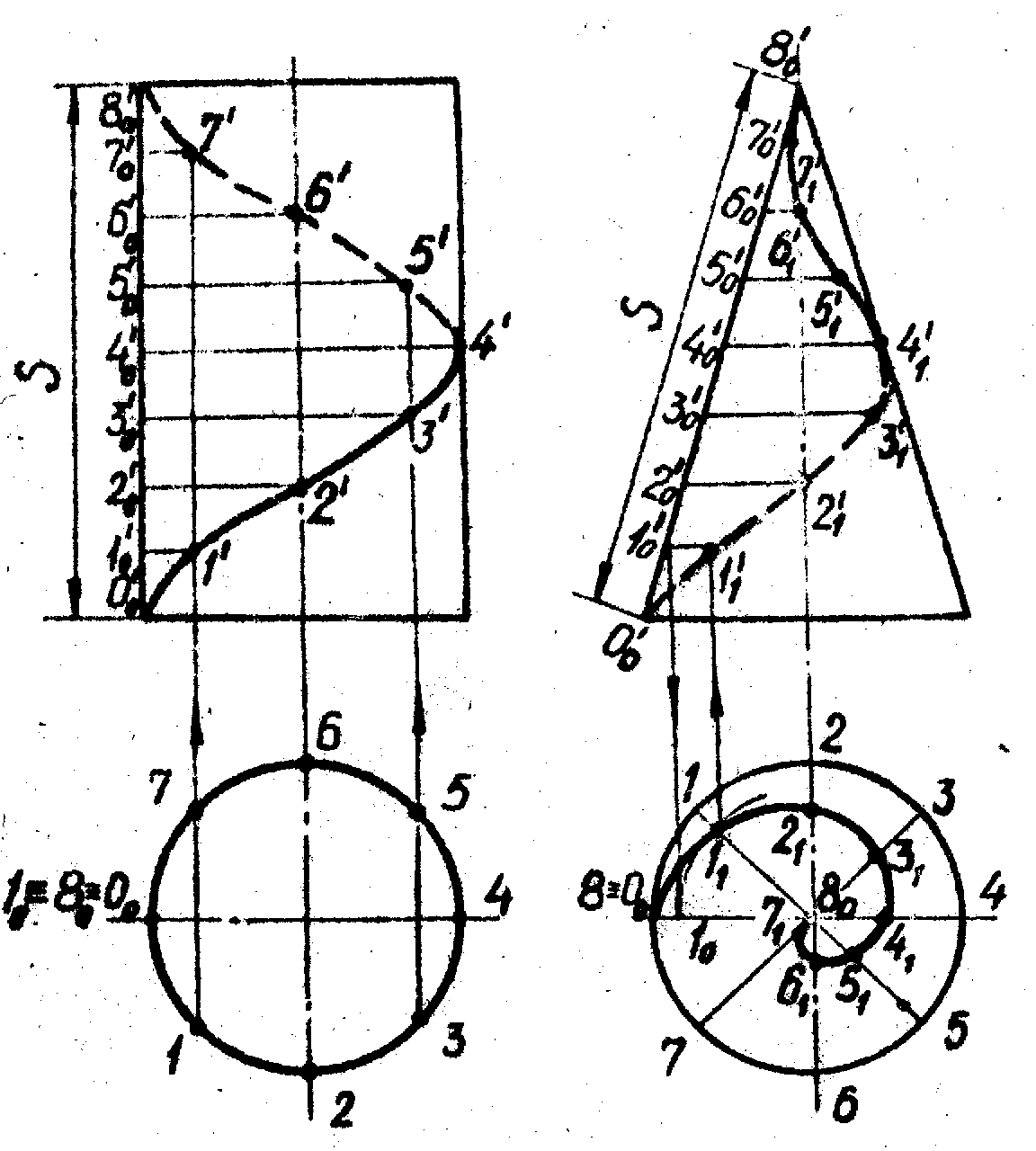
ис. 2




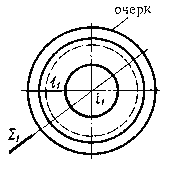
Рис. 3








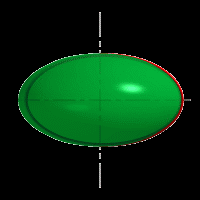
Рис. 4 Рис. 5 Рис. 6





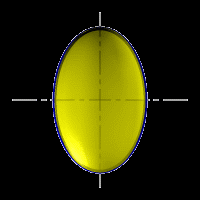
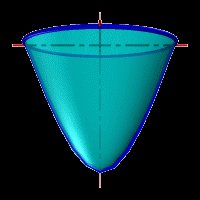
Рис. 7 Рис. 8 Рис. 9





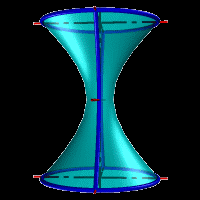
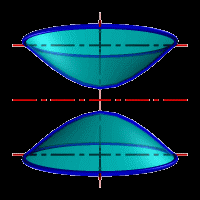
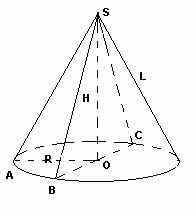
Рис. 10(а,б) Рис. 11








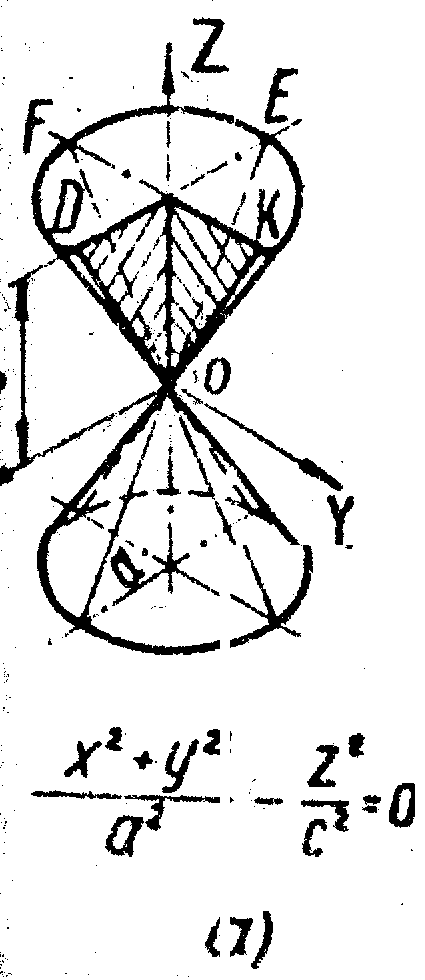
Рис. 12 Рис. 13





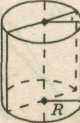
Рис. 14 Рис. 15 Рис. 16






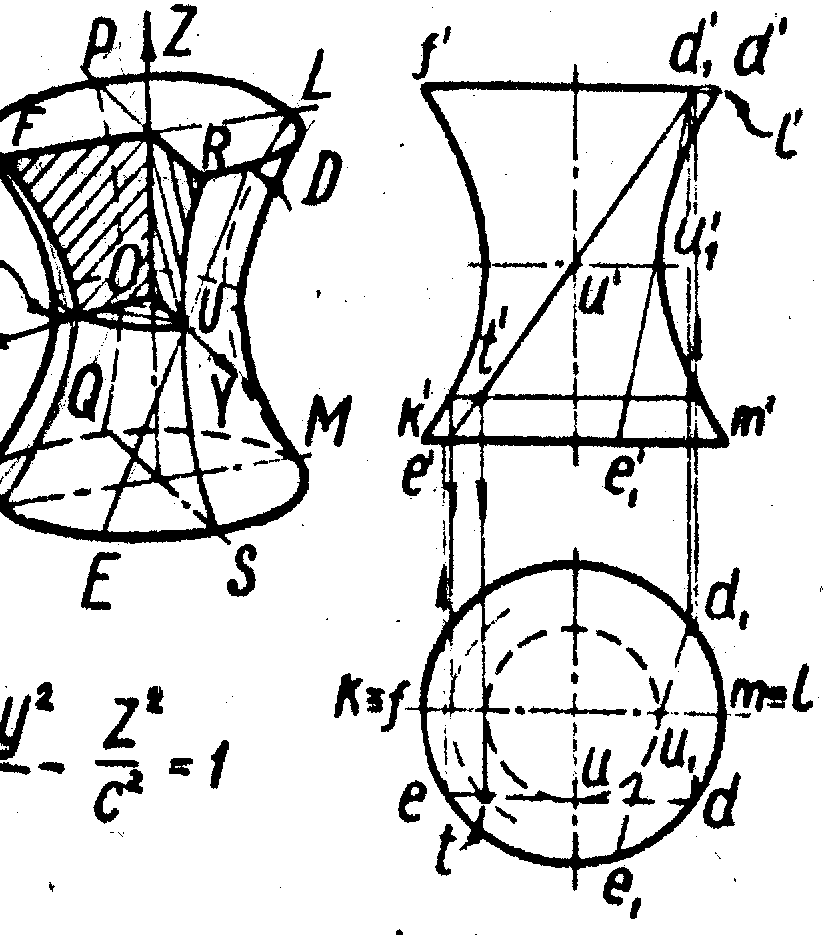
Рис. 17




Рис. 18





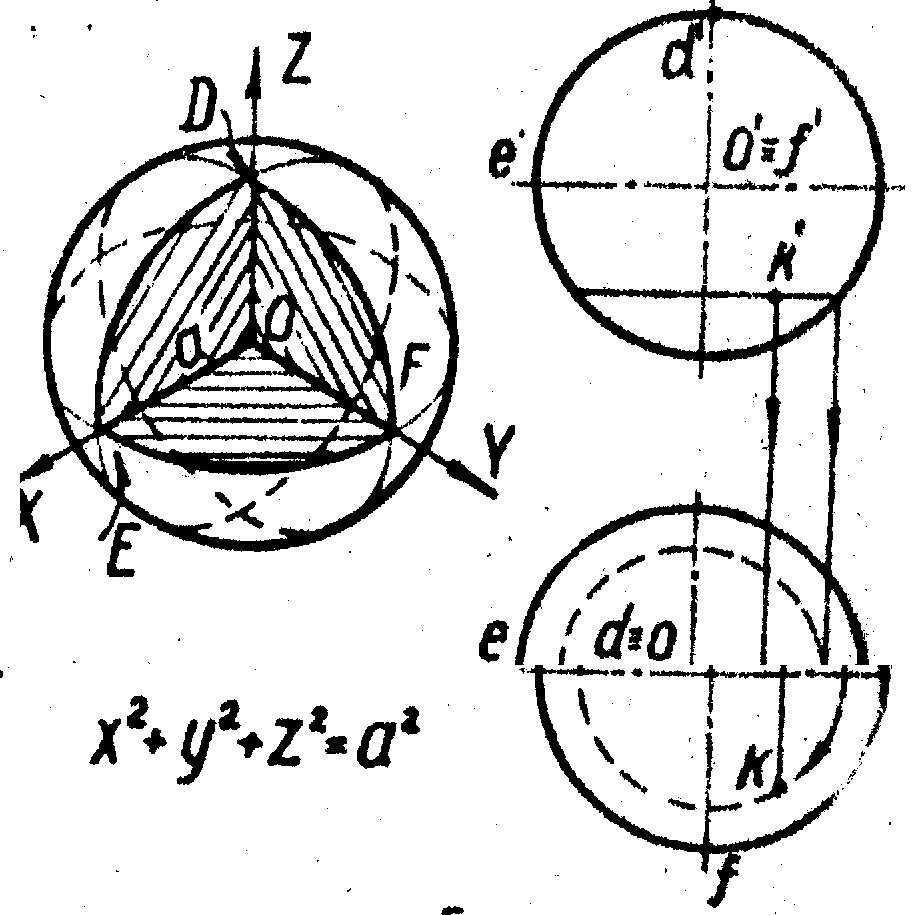
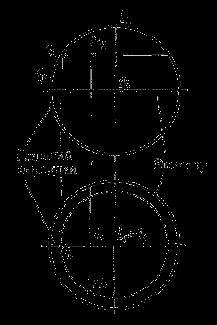
Рис. 19




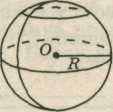
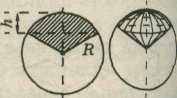
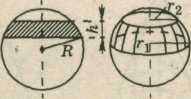
Рис. 20 Рис. 21 Рис. 22









Рис.23


Рис. 24







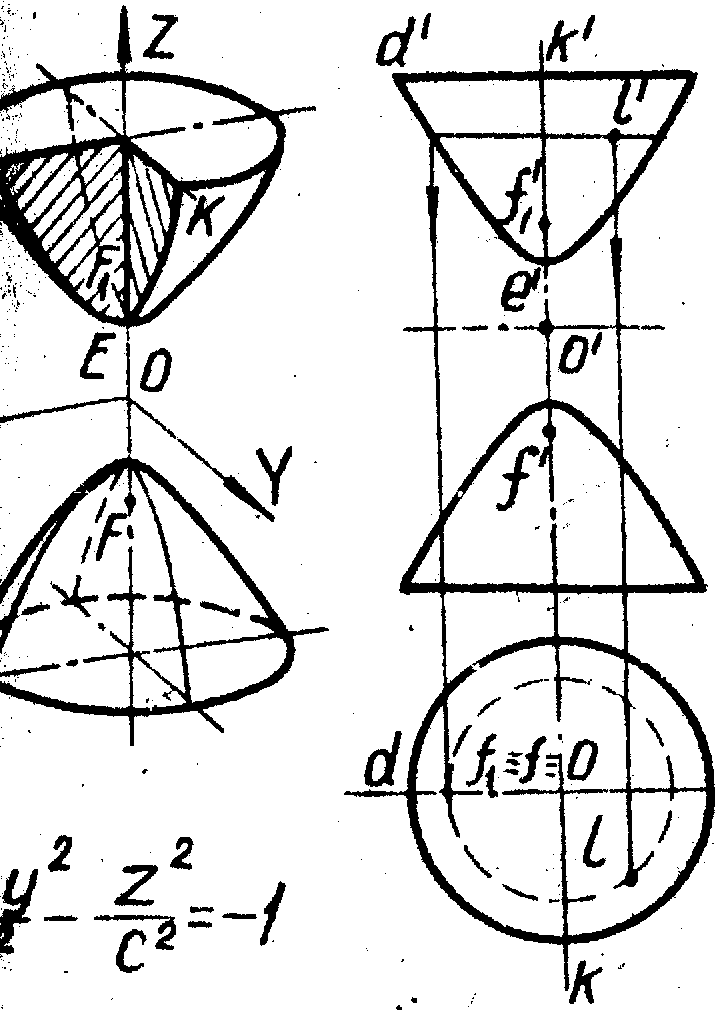
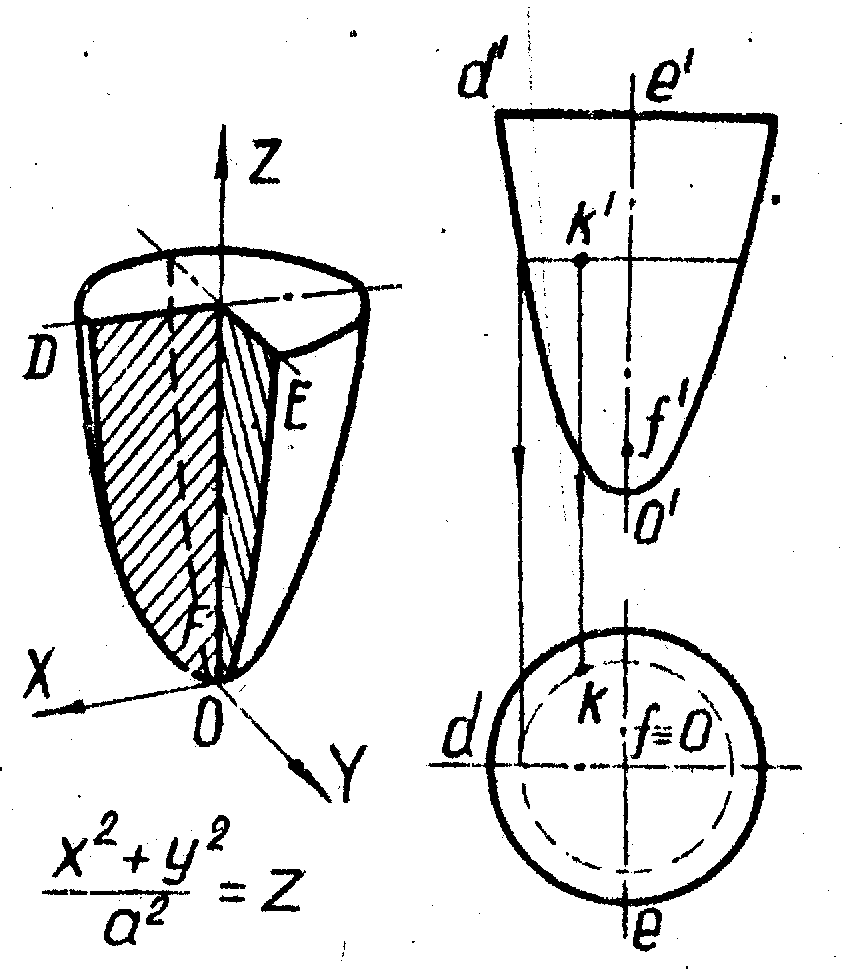
Рис. 25 Рис. 26






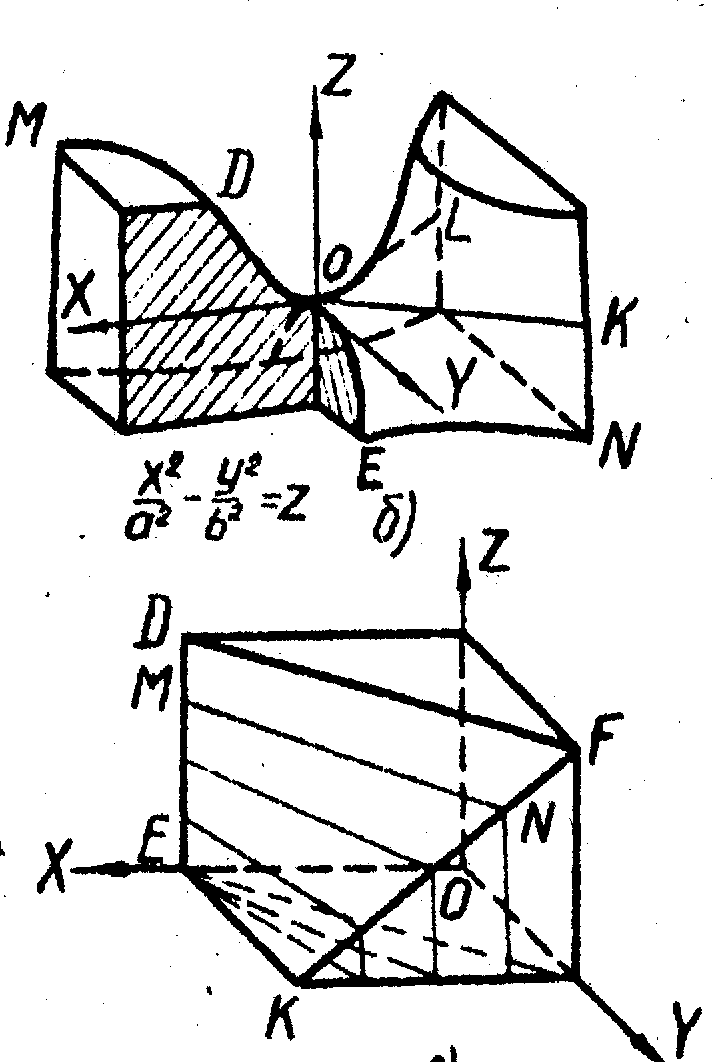
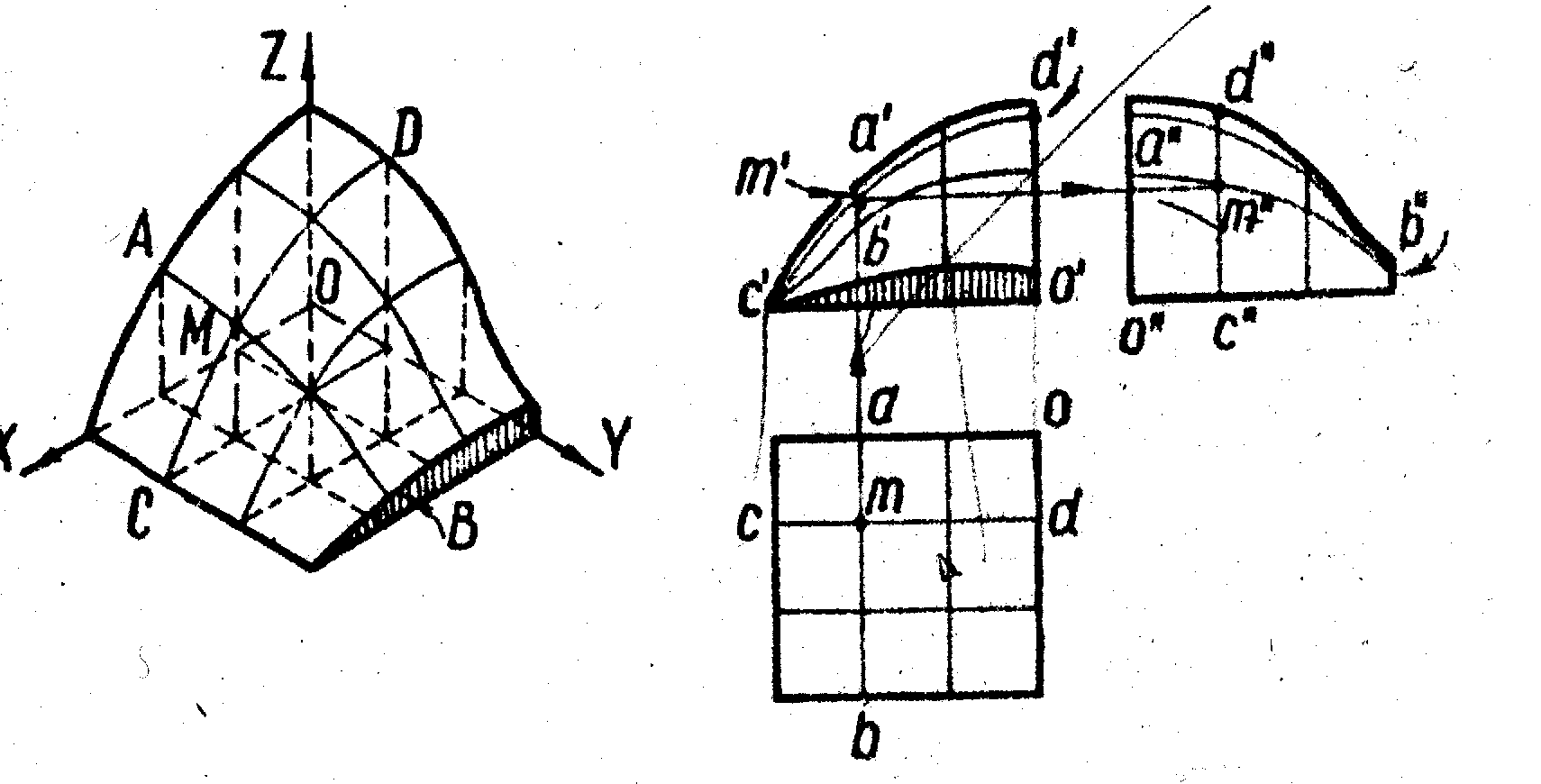
Рис. 27 Рис. 28





Однополостный гиперболоид вращения первой башни Шухова образован 80 прямыми стальными профилями, концы которых крепятся к кольцевым основаниям. Сетчатая стальная оболочка из ромбовидно пересекающихся профилей упрочнена 8 параллельными стальными кольцами, расположенными между основаниями. Высота гиперболоидной оболочки башни — 25,2 метра (без учёта высот фундамента, резервуара и надстройки для обозрения). Диаметр нижнего кольцевого основания — 10,9 метра, верхнего — 4,2 метра. Максимальный диаметр бака — 6,5 метра, высота — 4,8 метра. От уровня земли из центра основания башни до уровня дна резервуара поднимается красивая стальная винтовая лестница. В центральной части бак имеет цилиндрический проход с прямой лестницей, ведущей на смотровую площадку на верхней поверхности резервуара. Над смотровой площадкой на баке сделана гиперболоидная надстройка с прямой лёгкой лестницей, ведущей на более высокую малую смотровую площадку. Гиперболоидная надстройка смонтирована из 8 прямых профилей, упирающихся в кольцевые основания, между которыми расположено ещё одно упрочняющее кольцо. Верхняя площадка в 1896 году имела деревянный настил и ограждение (не сохранились до настоящего времени). Общая высота башни составляет 37 метров. Все стальные элементы конструкции башни соединены заклёпками.

Рис. 29




Рис. 30 Рис. 31





Рис. 32 Рис. 33





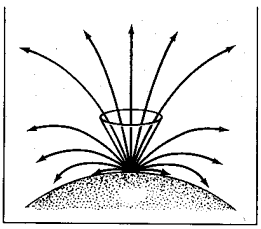
Рис. 34





Рис. 35


Рис. 36





Рис. 37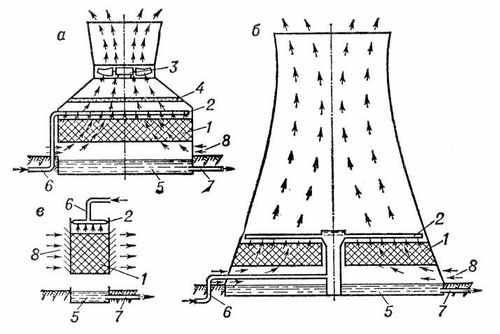

Рис. 38 Рис. 39





Рис. 40 Рис. 41





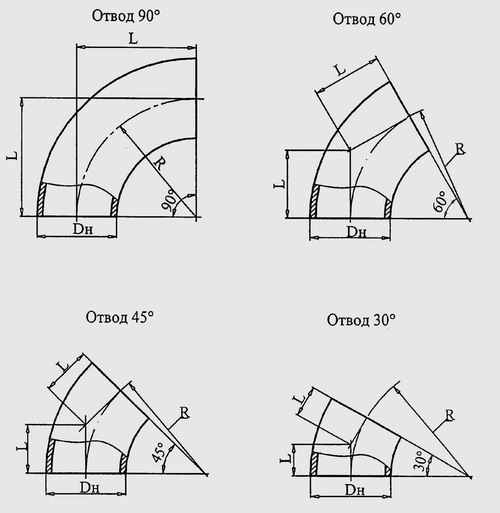
Рис. 42





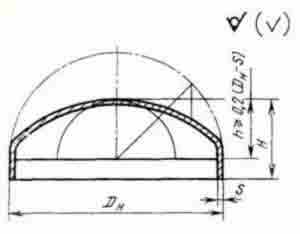
Рис. 43

^ СПИСОК ЛИТЕРАТУРЫ

1. Водяные тепловые сети: Справочное пособие по проектированию / И.В. Беляйкина, В.П. Витальев, Н.К. Громов и др.; Под ред. Н.К. Громова, Е.П. Шубина. – М.: Энергоатомиздат, 1988. – 376 с.: ил.
   
2. Математическая энциклопедия. Ред. Коллегия: И.М. Виноградов (глав. ред.) [и др.] Т. 1- М., «Советская энциклопедия», 1977 т. 1. А - Г. 1977. 1152 стб. с илл.
   

3. Математическая энциклопедия / Гл. ред. И.М. Виноградов. – М.: Советская Энциклопедия. т. 4 Ок – Сло. 1984. 1216 стб., ил.

4. Энциклопедический словарь юного математика / Сост. Э 68 А.П. Савин. – М.: Педагогика, 1985.- 352 с., ил.

5. Энциклопедия для детей. Т.11. Математика/Глав. Ред. Э68 М.Д. Аксёнова. – М.: Аванта+, 2000.- 688 с.: ил.